高阶非线性不确定多智能体系统自适应RBF神经网络协同控制

2020-09-28黄小龙陈阳舟

北京工业大学学报 2020年9期

黄小龙，陈阳舟

(北京工业大学信息学部，北京 100124)

领导者跟随一致性问题是指系统中有一个(或几个)智能体充当领导者，而其余个体都为跟随者智能体，其中领导者具有期望的状态轨线且其动态行为不受其他节点信息的影响.控制目标是为跟随者智能体设计基于邻居信息的分布式协议，使得所有智能体都能够渐近跟踪领导者的动态行为.领导者跟随结构是在许多生物系统中均存在的节能机制，并且其能够加强群体的通信和导向[1].所以，有领导者的多智能体系统也受到了越来越多学者的关注.

文献[1-2]针对一类满足Lipschitz条件的高阶非线性多智能体系统，设计基于观测器的鲁棒控制，解决多智能体系统的状态合围控制问题.文献[3]研究有向拓扑结构下离散时间多智能体系统的协调预见跟踪问题.文献[4]在具有输入时滞条件下，设计了一类滑模观测器，能够在有限时间内为跟随者发送领导者的信息.文献[5]研究了一类含有外部干扰和未建模动态的高阶非线性多智能体系统的分布式模糊自适应控制问题.文献[6]对领导者跟随混合阶多智能体系统的一致性问题进行了更为详尽的研究.文献[7]针对线性系统，提出了领导者跟随网络中异质多智能体系统达到输出一致的解决方案，当状态信息不易直接测量时，设计了一种基于状态观测器的动态调节器来重构状态.文献[8]针对二阶非线性系统，采用滑模控制算法，提出了一个有领导者的多智能体网络在有限时间之内达到状态一致性.文献[9]针对二阶非线性系统，利用神经网络的万能逼近功能对未知函数进行在线估计和逼近，获得一个基于神经网络的自适应协议.

本文研究了高阶非线性系统的协同跟踪控制问题.研究基于以下2个方面：

第一，现有的多智能体系统研究多集中于一阶和二阶系统，然而，在实际工程中，单连杆柔性关节机械手、机器人编队合作和同步发电机协调工作等是以高阶动力学建模的.以协调作战的无人机组为例，迫于环境变化突然改变运动方向，此时不但要求位置和速度一致，而且要求加速度协调统一.因此，研究此类高阶非线性系统不仅具有极为重要的理论价值，而且也有较强的工程实用价值[10].

第二，由于外界环境的干扰及自身系统参数的不确定性，导致研究对象往往具有未知且复杂的非线性动态，从而很难获得控制对象的精确数学模型，这种非线性动态的存在，系统可能由同构向异构转变，为非线性系统的协同控制带来困难[11].

针对上述问题，本文针对Brunovsky型高阶非线性多智能体协同跟踪控制进行了研究.该动力学系统的特点是每个追随者节点都通过一个高阶积分器耦合未知非线性动力学和未知外部干扰，每个节点动态可以完全不同[12].领导者节点是一个高阶非自治非线性系统，所有跟随节点对其动态都是未知的.本文提出分布式自适应径向基函数(radial basis function，RBF)神经网络控制算法，确保神经网络对非线性项进行在线逼近，以及消除持续有界扰动等不确定项对稳定性的影响，并设计出神经网络权值的自适应律，从而最终获得一个基于自适应RBF神经网络的自适应协议，该方法能够解决高阶非线性不确定多智能体系统的有领导者一致性追踪问题，保证最终有界跟踪误差.

本文给出了一种在弱连通的条件下，有领导者的高阶非线性不确定多智能体网络的一致性协议，并给出了相应的理论论证，通过例子和数值仿真都验证了本文提出方法的正确性和有效性.

1 预备知识和问题描述

1.1 图论基础和记号说明

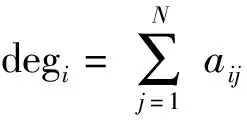
1.2 问题描述

考虑由N+1个智能体组成的系统，其中第i个智能体具有如下的Brunovsky非线性动态模型：

(1)

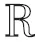
系统领导者0的动力学行为可描述为

(2)

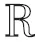
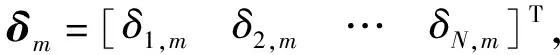
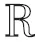
1){0}⊂Ωm；

2)∀δm(t0)⊂Ωm；

3)存在上确界Δm和时间Tm，在∀t≥t0+Tm时，有‖δm‖≤Δm.

对于智能体i，在t≥t0+Tm时，如果跟随误差是协同一致最终有界的，则跟随者状态xi,m(t)收敛到领导者x0,m(t)的邻域内.

第i个智能体局部邻域误差定义为

(3)

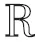
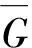
引理1[11，15]定义

q=[q1,q2,…,qN]T=(L+B)-11N

P=diag{pi}=diag{1/qi}

Q=P(L+B)+(L+B)TP

可知P和Q为正定矩阵.

证明：根据式(3)，进一步地，定义多智能体系统全局误差向量

(4)

根据假设1，矩阵L+B是非奇异的.在式(4)中，em=-(L+B)δm，由此可得

δm=-(L+B)-1em

所以

2 自适应协同跟踪控制器设计

对存在不确定性的领导者的多智能体系统，采用离线训练的神经网络显然是不合适的.为解决此类问题，本节设计了分布式神经网络控制器，采用在线自适应RBF神经网络控制方法，实现神经网络权值矩阵的自适应调整，以解决领导者跟随一致性问题.

2.1 滑模面函数设计

采用滑模变结构控制，主要是因为该控制算法在保证系统稳定性的同时，还具有快速响应的特性.

选取智能体i(i∈N)的滑模面函数为

ri=α1ei,1+α2ei,2+…+αM-1ei,M-1+ei,M

(5)

系数α1,α2, …,αM-1满足以s为自变量的多项式sM-1+αM-1sM-2+…+α1是Hurwitz的.那么如果ri是有界的，则ei也为有界的.进一步，随着ri→0，有ei→0.

定义滑模全局误差向量为r=[r1,r2,…,rN]T，那么，r=α1e1+…+αM-1eM-1+eM.

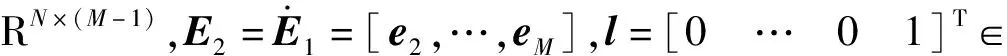
(6)

则有

E2=E1ΛT+rlT

(7)

由于Λ是Hurwitz矩阵,给出任何正数β,存在一个对称矩阵P1>0，使得李雅普诺夫方程成立，即

ΛTP1+P1Λ=-βIN

(8)

动态滑模误差r的导数为

下面引理3表明了ri(i∈N)的最终有界性，则ei也是有界性的.

引理3对于智能体i(i=1,2,…,N)，假设

|ri(t)|≤ψi，∀t≥t0

|ri(t)|≤ξi，∀t≥Tξi

时间Tξi>t0，上确界ψi>0，ξi>0.存在时间TΘi>t0，上确界Ψi>0，Θi>0，使得

‖ei(t)‖≤Ψi，∀t≥t0

‖ei(t)‖≤Θi，∀t≥TΘi

(9)

式(9)的通解为

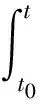
式中t0为初始时刻.

由于Λ是Hurwitz矩阵,存在φ>0和λ>0，使得

‖eΛ(t-t0)‖≤φe-λ(t-t0)

成立.进一步，结合‖l‖=1可得

‖ei(t)‖≤φe-λ(t-t0)‖ei(t0)‖+

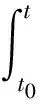
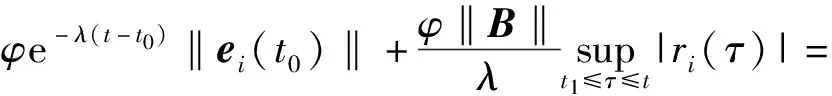
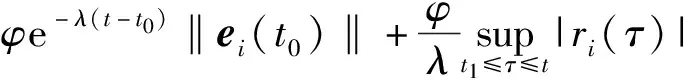
(10)

从式(10)可以看出，如果ri(t)有界，则‖ei(t)‖<∞，从而得到ei,m(t)对于所有的m=1,2,…,M都是有界的.因而由方程(5)可得

ei,M(t)=ri-α1ei,1(t)-α2ei,2(t)-…-αM-1ei,M-1(t)

也为有界的.因此，如果ri(t)<∞，那么‖ei(t)‖<∞，即‖ei(t)‖有界.

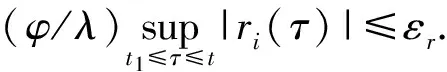
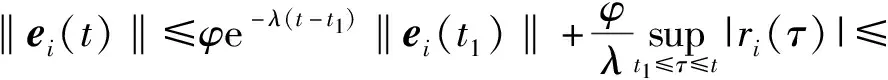
成立.由εe和εr的任意性可知，当t→∞时，有‖ei(t)‖→0成立，由此得到ei,m(t)→0对于所有m=1, 2，…，M-1成立.因而由方程(5)可得ei,M(t)=ri-α1ei,1(t)-α2ei,2(t)-…-αM-1·ei,M-1(t)→0.综上，当ri(t)→0时有ei(t)→0成立.引理得证.

注1从式(10)可以看出：较大的λ值会导致状态xi以较快的速率收敛到零.注意到λ的值取决于式(6)中的系统矩阵Λ，而Λ又与ri系数相关.因此，可以通过选取适当的系数α1,α2,…,αM-1, 得到令人满意的系统收敛速率.

2.2 基于RBF神经网络逼近未知函数f(·)

采用RBF神经网络逼近未知函数f(·)，隐含层第j个节点的输出为

式中：j=1,2,…,vi，vi为神经网络隐含层节点数；j为方差.

网络的输出由加权函数

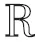
对未知函数fi(t,xi)进行逼近，采用系统状态xi,1(t)，xi,2(t)，…，xi,M(t)作为网络的输入，网络输出为

式中第i个智能体的神经网络估计权值为i(t)∈vi.

定义最优权值矩W=blkdiag{W1,W2,…,WN},估计权值=blkdiag{1,2,…,N},逼近误差ε=[ε1,ε2,…,εN]T,径向基函数向量可得全局非线性函数f(·)具有如下的形式:

f(x)=WTφ(x)+ε

(11)

f(x)的估计值为

(x)=Tφ(x)

(12)

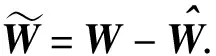
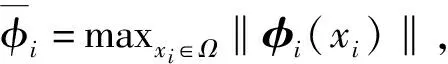
2.3 分布式控制器设计

设计每个智能体i分布式控制律ui和RBF神经网络的权值自适应律做如下假设.

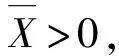
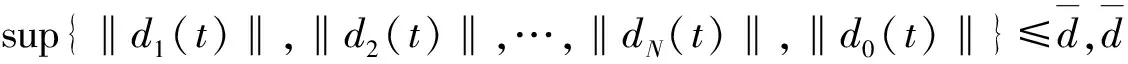
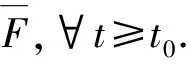
2.3.1 RBF神经网络的权值自适应律

设计RBF神经网络的权值自适应律为

(13)

可写成如下的简洁向量形式：

(14)

2.3.2 多智能体系统分布式控制协议

较大的外界扰动需要较大的切换增益，引起系统的抖振，控制协议采用神经网络对滑模控制进行补偿，为解决这一问题提供了有效的途径.

根据2.2节介绍，每个智能体i使用隐含层节点数为vi，设计每个智能体i分布式控制协议

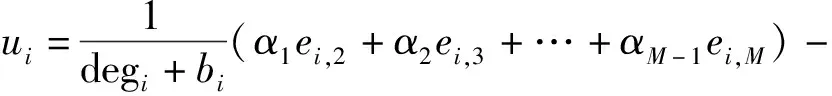
i(xi)+kri

(15)

分布式控制协议可等价地写成简洁向量形式

u=-(D+B)-1ρ-(x)+kr

(16)

控制增益满足

(17)

当m=1，2时，多智能体网络退化成2种特殊情形：一阶系统和双积分系统.

特别注意的是，RBF神经网络的权值自适应律式(13)和分布式控制协议式(15)适用于第i个智能体.

2.4 自适应RBF神经网络控制系统稳定性分析

定理1考虑N个跟随者式(1)和一个领导者0式(2)组成多智能体系统，假设1～4皆成立，使用RBF神经网络的权值自适应律式(13)和分布式控制协议式(15)，得到如下结果:

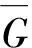
2)所有状态xi(t)是有界的.

证明：构建Lyapunov函数

V(t)=V1(t)+V2(t)+V3(t)

(18)

首先对V1(t)求导数，有

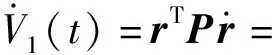
rTP[ρ-(L+B)(f+d+u-f01N)]

(19)

将式(16)代入式(19)，并考虑式(11)(12)和L=D-A，得

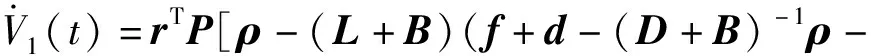
+kr-f01N)]=

rTPρ-rTP(L+B)(ε+d-f01N)-krTP(L+B)r-

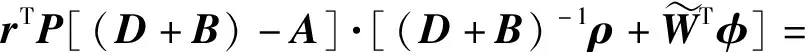
-rTP(L+B)(ε+d-f01N)-

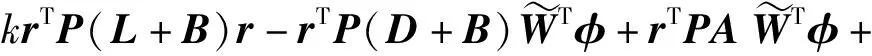
rTPA(D+B)-1ρ

对V3(t)求时间导数得

(20)

将式(7)代入式(20)，并考虑式(8)，得

因此

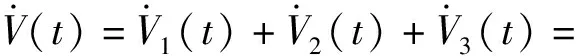
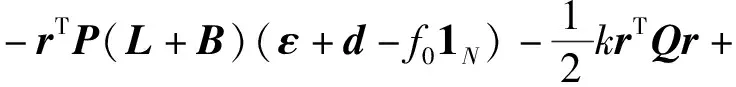
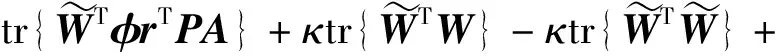
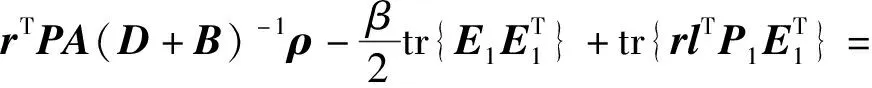
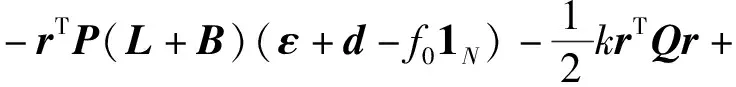
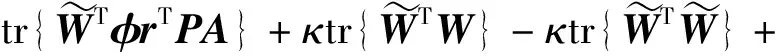
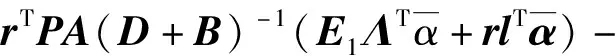
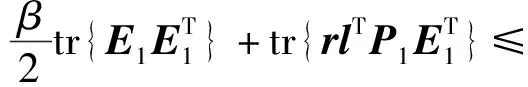
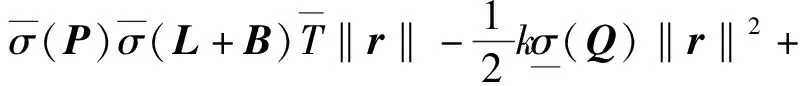
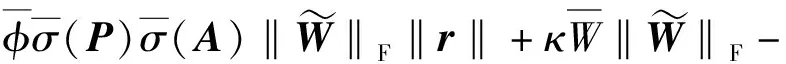
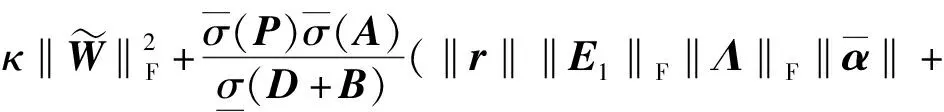
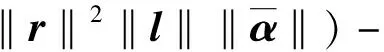
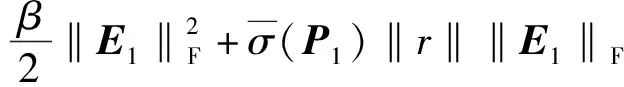
(21)

根据2.3.2节对γ、h和g的定义，式(21)可化为

(22)

系统实现渐近稳定的条件是Vz(z)为正定函数，即满足下面2个条件：

1)矩阵Ξ是正定的；

为了检验矩阵Ξ的正定性，可对各顺序主子行列式校验其是否大于0，即

β>0

βκ>0

解上述不等式，可得式(17)的条件.

易知‖ω‖1>‖ω‖，如果‖z‖≥Bd，上述条件2成立，可求得

因此，条件1和2皆满足，最终得到

Vz(z)是连续正定函数.

根据二次正定函数(18)，可以得到不等式

(23)

根据文献[18]定理4.10，存在有限时间T0，得到‖z(t)‖是有界的，满足关系

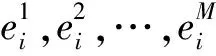
3 数值仿真

3.1 同构多智能体系统的一致性

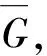
4个跟随者具有如下的三阶不确定非线性多智能体系统：

假设非线性函数fi的数学表达式与领导者相同，即

f(t,xi(t))=

-sinxi1-0.25xi2+1.5cos(2.5t)

领导者具有式(2)的动力学方程，其中，f0=-sinx01-0.25x02+1.5cos(2.5t).

对于网络G中第i个智能体，假设其包含外界扰动和传感器噪声等不确定性项统一建模为0.01sint.神经网络隐含层节点数为7个，网络的初始值为0，高斯函数参数设置为

多智能体系统初始状态信息为

三阶系统的所有智能体的各阶状态轨迹如图2～4所示，4个同构跟随者的位置状态都渐渐逼近领导者0的位置状态，即实现领导跟随一致性.

3.2 异构多智能体系统的一致性

为了说明所提协议能够应用于异构多智能体系统，考虑如下4个智能体：

假设非线性函数fi的数学表达式为

f1(t,x1(t))=-sinx11-0.2x12+2cos(2.5t)；f2(t,x2(t))=-1.2sinx21-0.25x22；f3(t,x3(t))=-0.8sinx31-0.25x32+cos(3t)；f4(t,x4(t))=x41-0.25sinx42

控制器和神经网络的参数、网络拓扑结构、系统的初始状态、不确定项di(t)、领导者的系统模型皆与3.1节相同.三阶系统所有智能体的各阶状态轨迹如图5～7所示，4个异构跟随者的位置状态都渐渐逼近领导者0的位置状态，实现了状态的一致性.

上述仿真结果表明，在设计控制协议作用下，系统跟随者状态轨迹在有限时间内到达切换流形，从而所有智能体的各阶状态都能相应地收敛到一起,即

从而验证了定理的正确性.通过同质和异质多智能体系统仿真比较，验证了所提出的自适应一致性协议不仅适用于同质多智能体系统，也可应用于异质多智能体系统.

另外，从状态轨迹图可知，在不改变领导智能体的初始条件下，利用牵制控制技术，将领导者的状态信息传递给跟随者，而异质跟随智能体通过控制输入，能够逼近同质跟随智能体的状态.

注3针对系统中存在外界扰动和不确定项问题，目前主要有鲁棒控制方法和状态观测器方法.采用鲁棒控制对外界扰动有一定抑制作用，但不能有效地消除外界扰动对一致性的影响，如文献[19].目前较为常用的方法是采用状态观测器，对多智能系统不确定项进行估计来补偿未知项，实现多智能体的一致性，而且设计的是针对线性系统[20].本文针对高阶非线性不确定多智能体系统展开研究，对系统中非线性部分采用RBF神经网络进行逼近，设计滑模控制器对外界扰动进行了补偿，使多智能体实现镇定，从而实现了领导者跟随者一致性问题.