最小最大二点集覆盖问题分析及改进算法设计

徐 弈， 陈 莹

（1.西安理工大学 经济与管理学院，陕西 西安710054；2.西安交通大学 管理学院，陕西 西安710049）

0 引言

近些年，选址问题中的二中心问题及其扩展问题已成为主要的研究方向之一，其中平面点集的二中心问题更是人们关注的重点问题，该问题定义如下：给定平面点集P，求两个圆的并覆盖整个点集，使得两个圆半径的最大值最小。Drezner在1984年首次给出了O（n3）时间复杂性的算法［1］。1994年，Agarwal和Sharir两人给出了第一个接近平方级别的算法—O（n2log3n）的确定时间算法［2］，而该算法的中心思想来源于Hershberger和Suri两人于1991年给出的二中心问题的判定问题解法［3］。所谓判定问题，即为给定半径r＞0，问是否存在两个半径为r的全等圆覆盖P。他们给出这个判定问题可以在O（nlogn）的时间内求解。紧接着在1994年，Jaromczyk和Kowaluk给出了O（n2logn）时间复杂性的算法［4］。作为一个突破，通过结合之前Hershberger和Suri提出的判定问题解法，1997年Sharir利用参数搜索技巧设计并行算法，将求解二中心问题的时间复杂性降到了O（nlog9n）［5］，这是历史上第一个接近线性时间的确定算法。同年，同样运用参数搜索设计并行算法，Eppstein给出了O（nlog2n）的期望时间算法［6］。1999年，Chan对Sharir给出的算法又做了进一步改进，给出了到目前为止最快的算法，其时间复杂性为O（nlog2nlog2logn）［7］。对离散二中心问题，即限定两个圆的圆心在点集P内，Hershberger和Suri在他们求解判定问题的文章中给出离散二中心问题可以在O（n2logn）时间内求解［3］。通过运用Katz和Sharir提出的几何优化问题中的扩展方法，Agarwal和Sharir等人给出目前为止最快的算法，其时间复杂性为O（n4/3log5n）［8］。而二中心问题的在线情况，由Zhu等人于2013年提出并给出近似比为5.611的近似算法［9］，接着该问题在2015年被Kim等人将近似比改进到1.865［10］。

本文着重讨论二中心问题的一个扩展问题-最小最大二点集覆盖问题，并对该问题已有算法进行改进。2003年，Huang等人考虑了α连通二中心问题［11］。他们首先考虑这个问题的判定问题，即：给定半径r＞0，是否存在两个半径为r的全等圆，使两圆的并覆盖P并且圆心距与半径之比小于常数α。通过最远点Voronoi图与点集中心包的关系，他们给出这个问题的判定问题可以在O（n2log2n）的时间内求解。接着在2006年，通过运用参数搜索设计并行算法，他们给出α连通二中心问题可以在O（n2log2n）的期望时间内求解［12］。2019年，Xu等人考虑这个问题的衍生问题，即圆心限制在点集内部的混合与离散情况，对这两种情况他们分别给出复杂性为O（n2log2n）和O（n2logn）时间的确定算法［13］。2014年，Kavand提出了（n，1，1，α）中心问题，即求解两个圆使其分别覆盖点集P，满足其圆心距不小于α且大圆的半径最小［14］。通过运用最远点Voronoi图［15～17］，他们证明该问题最优解的两个圆一定全等，并且给出O（nlogn）时间复杂性的算法。本文所考虑的最小最大二点集覆盖问题也可以看成是二中心问题的扩展问题，问题的描述如下：

问题1给定两个平面点集P1和P2，分别包含m和n个点，求两个圆分别覆盖P1和P2，满足两个圆的半径与圆心距三者中的最大值最小。

对该问题，2006年Huang等人通过运用参数搜索设计并行算法给出这个问题可以在O（（m+n）log（m+n））的确定时间内求解［9］。但是注意到，他们所设计的并行算法，需要处理器的个数为O（m+n），而当m和n足够大时，这是不可能实现的。为了改进这个缺陷，本文同样给出接近线性时间的确定时间算法，但是与之不同的是本文提出的算法不需要运用并行计算，从而大大提高了算法的可实现性.本文结构如下：第1节回顾点集的最远点Voronoi图与点集中心包的关系；第2节给出最小最大二点集覆盖问题的最优解几何结构；第3节重点研究在同一个半径变化过程中，两个点集中心包之间的最近距离变化关系；第4节通过该变化关系设计最小最大二点集覆盖问题算法；第5节给出结论与展望。

1 最远点Voronoi图与点集中心包关系

在讨论最小最大二点集覆盖问题之前，先给出本文所用到的一些符号：记P1和P2为平面上分别包含m和n个点的点集，D（o，r）为以o为圆心，r为半径的圆盘，C（o，r）为圆盘D（o，r）的边界（即圆圈），称C（o，r）上的点为控制点。对任意两点｛x，y｝，记d（x，y）为两点之间的欧氏距离，lx，y为过两点的线段。在讨论设计算法之前，首先介绍一个点集的中心包与最远点Voronoi图之间的关系［11］。对任意点集P，其对应以r为半径的中心包定义如下［3，11］：

定义1对点集P而言，其以r为半径的中心包CHr（P），是以P中的所有点为圆心，r为半径的圆盘的交，即CHr（P）∩p∈PD（p，r）。

对点集P的中心包，有以下几个关键性质［11］。

性质1记点集P的最小覆盖圆半径为r0，则CHr（P）＝Ø当且仅当r＜r0。

性质2点p在CHr（P）内当且仅当p到P中的最远点距离小于等于r。

由性质2与最远点Voronoi图的定义，又得到如下性质：

性质3CHr（P）上的每个弧在所对应圆心的最远点Voronoi区域内。

由性质1、性质2和性质3可以得到以下关键性质：

性质4点集P的中心包CHr（P）弧的个数随半径r的变化如下：随着半径的增加，每当半径超过P的最远点Voronoi图的一个交点到其对应最远点之间的距离，则中心包弧的个数增加1。

2 最优解几何结构与性质

记P1和P2的最小覆盖圆分别为D（o1，r1）和D（o2，r2）（不失一般性，假设r1≥r2），同时令最小最大二点集覆盖问题最优解所对应P1和P2的覆盖圆分别为D（）和D（），由问题1可以得到其等价形式：

问题2最小最大二点集覆盖问题等价于两个全等的圆分别覆盖P1和P2，并且要求半径与圆心距二者中的最大值最小。

本文着重通过点集中心包的性质来研究问题2。由问题2可以看出，此时最优解结构存在两种情况：

情况1圆心距小于等于圆半径。

由于两个点集P1，P2已经给定，因此可以通过计算这两个点集各自的最小覆盖圆进行检测。如果满足d（o1，o2）≤r1，则此时已然得到最优解；否则，计算点集P2在r1下的中心包CHr1（P2），如果满足o1到CHr1（P2）的最短距离小于等于r1，则此时仍然得到最优解，这里取该最近点为覆盖P2的圆所对应的圆心，r1为覆盖半径即可。

情况2圆心距大于圆半径。

对这种情况，最优解半径一定大于max｛r1，r2｝。从直观角度看，这时需要同时增加两个点集各自覆盖圆的半径，并且同时将两个圆的圆心相互靠拢，直到两圆圆心距与半径相同时得到最优解。此时，最优解情况可以分为以下三种：

情况2a最优解由两个控制点决定。

情况2b只有一个圆有一个控制点。

情况2c两个圆至少都有两个控制点。针对情况2a，此时有：

引理1这两个控制点和两个圆心共线。

证明记这两个控制点为a和b，其中a∈C（，r），b∈C（，r）。不失一般性，假设a与两个圆心不共线，则一定在的邻域Nε（）内存在一个新的圆心，使得D（，r）仍然能够覆盖P1。同时，在的邻域Nε／2（）内也一定存在一个新的圆心，使得D，r-ε／10）能够覆盖P2并且满足d（）＜r，注意到这时D（，r）和D（，r-ε／10）均不是点集P1和P2的最小覆盖圆，这意味着一定存在两个半径更小，且两圆圆心距小于r的圆分别覆盖P1和P2，这与最优解假设相矛盾（见图1）。

通过引理1，直观地可以看出和一定分别在C（a，r）和C（b，r）上，又因为｛a，b｝为两个圆的控制点，再由中心包定义，可以得到和一定分别在CHr（P1）和CHr（P2）的一条弧上。

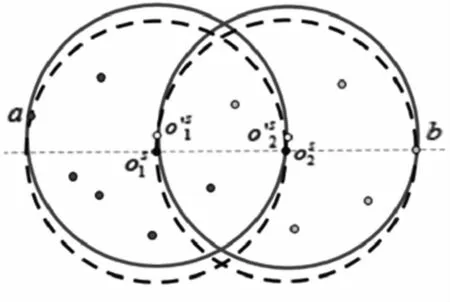
图1 引理1说明

针对情况2b，此时与情况2a类似的有：

引理2这个控制点与两个圆心共线。

证明设b为圆D，r）的唯一控制点。若b不与两个圆心共线，则与引理1类似的可以证明，一定存在两个圆分别覆盖P1和P2，并且满足max｛r-ε／10，d（）｝＜r（见图2）。

图2 引理2说明

由引理2可知，记另一个圆的两个控制点分别为a1和a2，有在C（a1，r）和C（a2，r）的交点上，在C（b，r）上，即有一定在CHr（P1）的一个顶点上，一定在CHr（P2）的一条弧上。

针对情况2c，这两个圆都至少有两个控制点。不失一般性，假设这两个圆各自只有两个控制点，按照逆时针方向，记为｛a1，a2｝和｛b1，b2｝，可以得到以下最优结构

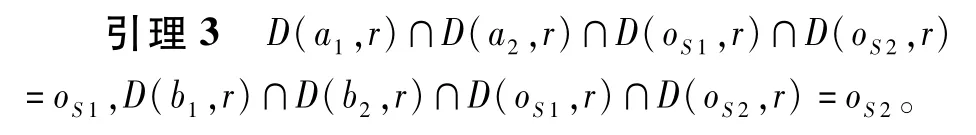
证明假设D（a1，r）∩D（a2，r）∩D（oS1，r）∩D（oS2，r）不止有oS1这一个点。则此时一定存在一个新的圆心，使得D（，r）能够覆盖P1∪满足此时的情况有两种：（1）｛a1，a2｝分布在过两圆心的直线lo S1，o S2的同侧（见图3（a））；（2）∠＞180°（以逆时针方向，见图3（b））。此时，与引理1，引理2证明类似，一定存在两个半径更小，且圆心距小于r的圆覆盖P1和P2。同理可证D（a1，r）∩D（b2，r）∩D（oS1，r）∩D（oS2，r）＝

这时，在C（a1，r）和C（a2，r）的交点上在C（b1，r）和C（b2，r）的交点上，由｛a1，a2｝和｛b1，b2｝分别为两圆的控制点，有和分别在CHr（P1）和CHr（P2）的一个顶点上。下一节将重点对这种结构给出相关分析。

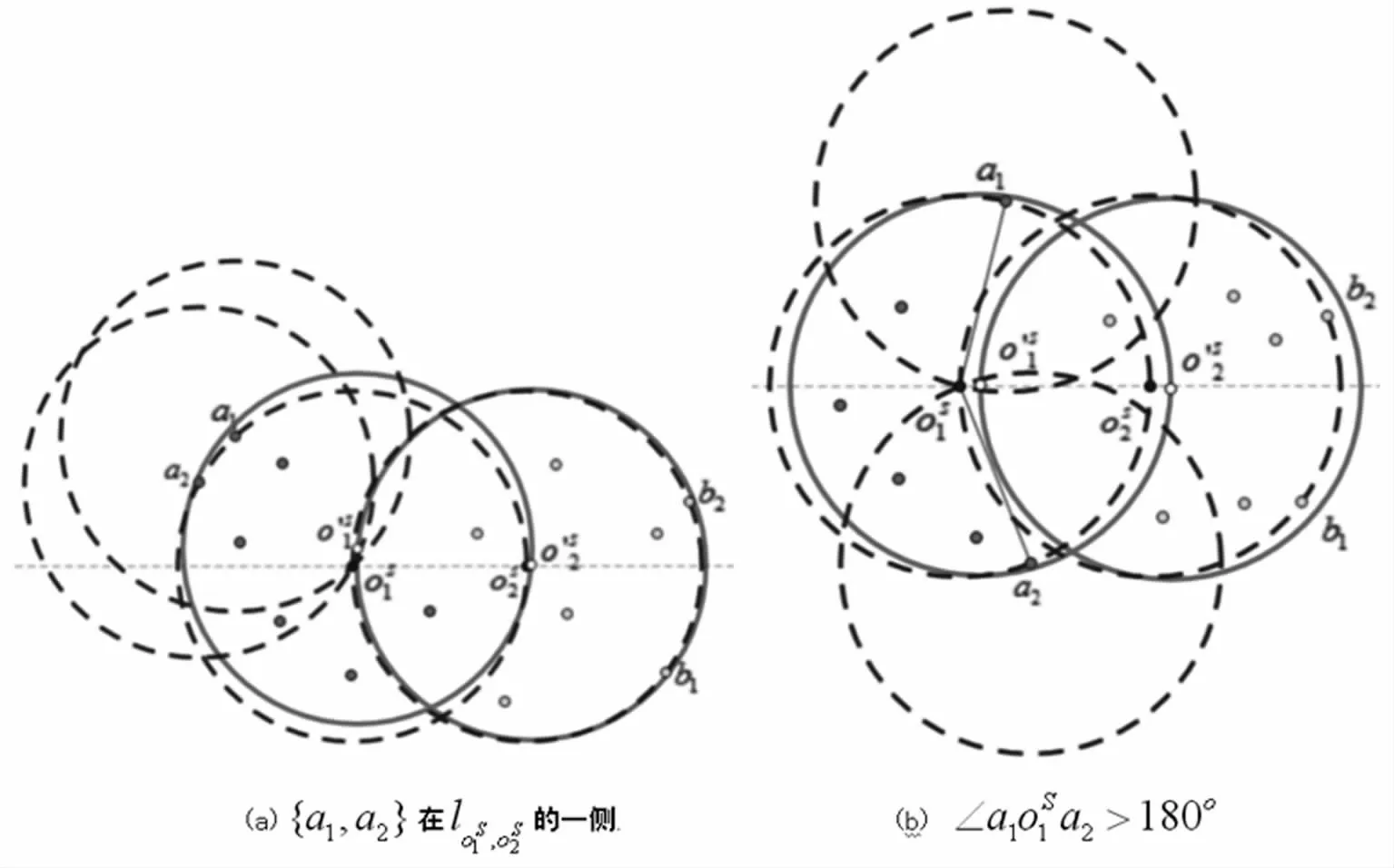
图3 引理3说明

3 两动态中心包之间最近距离变化分析

本节对两个动态中心包之间最近距离的几何结构性质进行分析。对给定点集P，Huang等人发现在半径的变化过程中，P的中心包的组合性质与点集的最远点Voronoi图紧密相关（即性质4）。基于这个重要的性质，他们提出连通二中心问题可以在接近平方级别的期望时间内求解［11］。然而，在该问题的子算法中，牵扯到对两个点集的中心包（假设两个点集分别含有m和n个点）在同一个半径r的变化过程中，这两个中心包的组合性质不发生变化时如何求解最优半径。他们给出该问题可以在O（log2（m+n））的时间内通过设计并行算法来求解。事实上，通过运用一些几何性质，这个子问题可以在常数时间内求解，并且不需要运用并行计算，同时该算法可以完美求解最小最大二点集覆盖问题。

注意到，对最优解几何结构的第二种情况，只需要找到一个临界半径，满足在这个半径下CHr（P1）和CHr（P2）之间的最近距离等于该半径即可。为了解决该问题，本节提出以下三个关键引理。对两个点集P和Q，在同一个半径r下，记这两个中心包之间最近距离的控制点分别为s1和s2。首先给出第一个引理。

引理4若s1和s2分别在CHr（P）和CHr（Q）的一条弧上，则在半径增加到r′的过程中，如果两个中心包的组合性质不发生变化时，CHr′（P）和CHr′（Q）之间最近距离的控制点仍在对应两个弧上。

证明记s1和s2分别在弧ar和弧br上。连接s1和s2，作两条直线l1和l2垂直于ls1，s2。此时有l1与弧ar相切，l2与弧br相切（见图4（a））。由中心包的凸性，可以得到当半径增加到r′时，CHr′（P）和CHr′（Q）之间最近距离的控制点仍在弧ar′和弧br′上（见图4（b））。

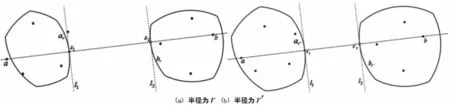
图4 引理4说明，其中r＜r′，s1和s2均在弧上

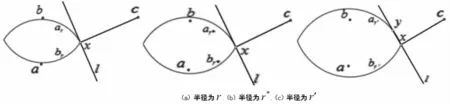
图5 性质5说明，其中r＜r*＜r′，r*是临界半径，此时l与弧ar*相切

在给出第二个关键引理之前，先给出一个性质并加以证明：

性质5给定三个点｛a，b，c｝和半径r，记x为弧ar和弧br的交点，l为过点x且垂直于lc，s的直线。如果l与弧ar仅有一个交点x，与弧ar′有不止一个交点（r＜r′），则一定存在一个临界半径r*，使得l与弧ar*相切。

证明当半径为r时，直线l与弧ar相交于x点（见图5（a））；当半径为r′时，l与弧ar′相交于x和y点，同时注意到此时有y在弧ar′上（见图5（c））。因此，随着半径的增加，可以得到a点从直线lc，x的一侧连续移动到另一侧，则一定存在一个临界半径r*使得｛a，c｝和x是共线的。这时，l与C（a，r*）相切（见图5（b））。

由上述事实，给出第二个关键引理。

引理5假设s1为弧ar和弧cr的交点，s2在弧br上，其中｛a，b，c｝为圆心。在半径从r增加到r′的过程中，如果两个中心包的组合性质不发生变化，则这两个中心包CHr′（P）和CHr′（Q）之间的最近距离对应的两个控制点有如下三种情形：（1）仍然是一个为弧ar′和弧cr′的交点，另一个在弧br′上；（2）一个在弧ar′上，另一个在弧br′上；（3）一个在弧cr′上，另一个在弧br′上。

证明令s1′和s2′为CHr′（P）和CHr′（Q）之间最近距离的两个控制点，由引理2，有｛b，s1，s2｝三点共线。连接s1和s2，过s1和s2分别作l1和l2垂直于ls1，s2，则有l2与弧br相切。因为在半径增加到r′的过程中，两中心包的组合性质不发生变化，则有：如果没有弧与l1相交，则由于变化过程拓扑结构不发生变化，两中心包最近距离的控制点仍旧落在弧ar′和弧cr′的交点以及弧br′上；否则，由于中心包的凸性，只会有CHr′（P）的一条弧与l1相交（不可能有大于一条弧与l1相交，如此做中心包则不为凸），不失一般性，假设弧cr′与l1相交。

接下来证明只有在弧cr′上的点有可能是距离弧br′最近的点。由于在半径增加的过程中，弧cr′与l1产生了第二个交点（除去s1′），由性质5可以得到，一定存在一个临界半径r*，使得弧cr*与l1相切。这时中心包CHr*（P）和CHr*（Q）最近距离的两控制点均在两条弧上，再由引理4，∀r′≥r*，CHr′（P）和CHr′（Q）最近距离的两控制点一定一直在两条弧上（即当r′≥r*时，此时与引理4情况相同）。图6给出一个例子，其中r1＜r2＜r3，r2是临界半径。当半径r′＞r2时，两个中心包之间最近距离的两控制点为一个在弧cr′上，一个在弧br′上。同理可证弧ar′与l1相交的情况。

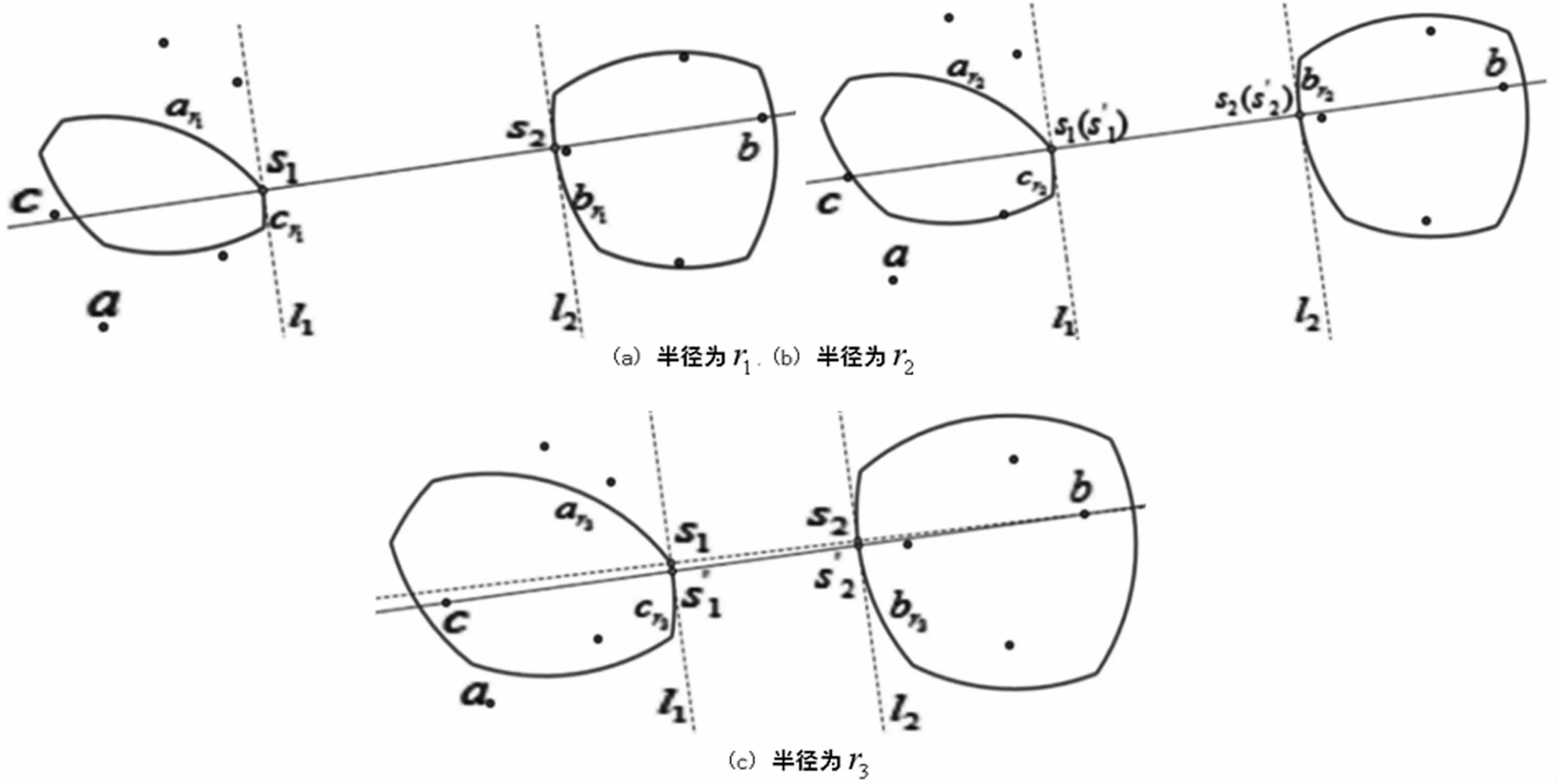
图6 引理5示例，r1＜r2＜r3，r2是临界半径。l1与弧cr2相切，s1′在弧cr3上，s2′在弧br3上

最后给出第三个关键引理。

引理6记s1为弧ar和弧cr的交点，s2为弧br和弧d r的交点，其中｛a，b，c，d｝为圆心。在半径从r增加到r′的过程中，如果两个中心包的组合性质不发生变化，则这两个中心包CHr′（P）和CHr′（Q）之间最近距离对应的两个控制点有如下三种情形：（1）一个在弧上cr′，另一个在弧上br′；或者一个在弧ar′上，另一个在弧d r′上；（2）一个是弧ar′和弧cr′的交点，另一个在弧br′或弧d r′上；或者一个是 弧br′和 弧d r′的 交 点，另 一 个 在 弧ar′或 弧cr′上；（3）一个是弧ar′和弧cr′的交点，另一个是弧br′和 弧d r′的 交 点。

证明令s1′和s2′为CHr′（P）到CHr′（Q）最近距离的两个控制点。连接s1和s2，过s1和s2分别作l1和l2垂直于ls1，s2。当半径增加到r′时，由于两个中心包的组合性质不发生变化，只会分别有CHr′（P）到CHr′（Q）的一段弧与l1和l2相交。接下来给出，如果弧cr′与l1相交，则只可能弧br′与l2相交。否则，假设弧d r′与l2相交，记这时CHr′（P）到CHr′（Q）最近距离的两控制点为u和v，其中u在弧cr′上，v在弧d r′上。由于两个中心包的半径增加速度是一致的，并且由中心包的凸性，u和v之间的距离不可能小于d（）（否则中心包不为凸，或者其中一个中心包每条弧增长速度不一致），因此，弧d r′不可能与l2相交。同理可以证明如果弧ar′与l1相交，则只可能弧d r′与l2相交。随着半径继续增加，会发生如下几种情况。

情况1在半径增加到r′的过程中，存在两个临界半径和），其中当半径增加到时，弧cr*1与l1相切，当半径增加到时，弧br*2与l2相切。则根据半径增加过程中两个中心包的组合性质不发生变化，∀r1≤，CHr1（P）和CHr1（Q）之间最近距离控制点为弧ar1和弧cr1的交点以及弧br1和弧d r1的交点；∀，由引理5，CHr2（P）和CHr2（Q）之间最近距离的两控制点一个在弧上，另一个为弧br2和弧d r2的交点；，由引理4，CHr3（P）和CHr3（Q）之间最近距离的两控制点一个在弧cr3上，一个在弧br3上。此时，有lb，c与CHr3（P）和CHr3（Q）在弧cr3和弧br3均有交点，并且两交点即为两中心包最近距离控制点。图7给出一个例子，其中r1＜r2＜r3＜r4，r2和r3为临界半径。当r＝r2时，l1与弧cr2相切；当r＝r3时，l2与弧br1相切；当半径继续增加到r4，则两中心包的最近距离控制点s1′和s2′分别在弧cr4和弧br4上。

情况2在半径增加到r′的过程中，假设存在一个临界半径r*。当半径增加到r*时，l1与弧ar*和弧cr*均不相交，而l2与弧br*或弧d r*其中之一相切（l1与弧ar*或弧cr*其中之一相切，l2与弧br*和弧d r*均不相交的证明类似），则在半径从r增加到r′的过程中，CHr′（P）与CHr′（Q）的最近距离的控制点一个为弧ar′和cr′的交点，另一个在弧br′上或弧d r′上（当r′≥r*），或者为弧br′与弧d r′的交点（当r′＜r*）。

情况3在半径增加到r′的过程中，如果l1与弧ar′和弧均不相切，l2与弧和弧d r′均不相切，则在半径增加过程中，CHr′（P）与CHr′（Q）之间最近距离的两控制点仍为两个弧的交点。至此，完成了对引理的全部证明。

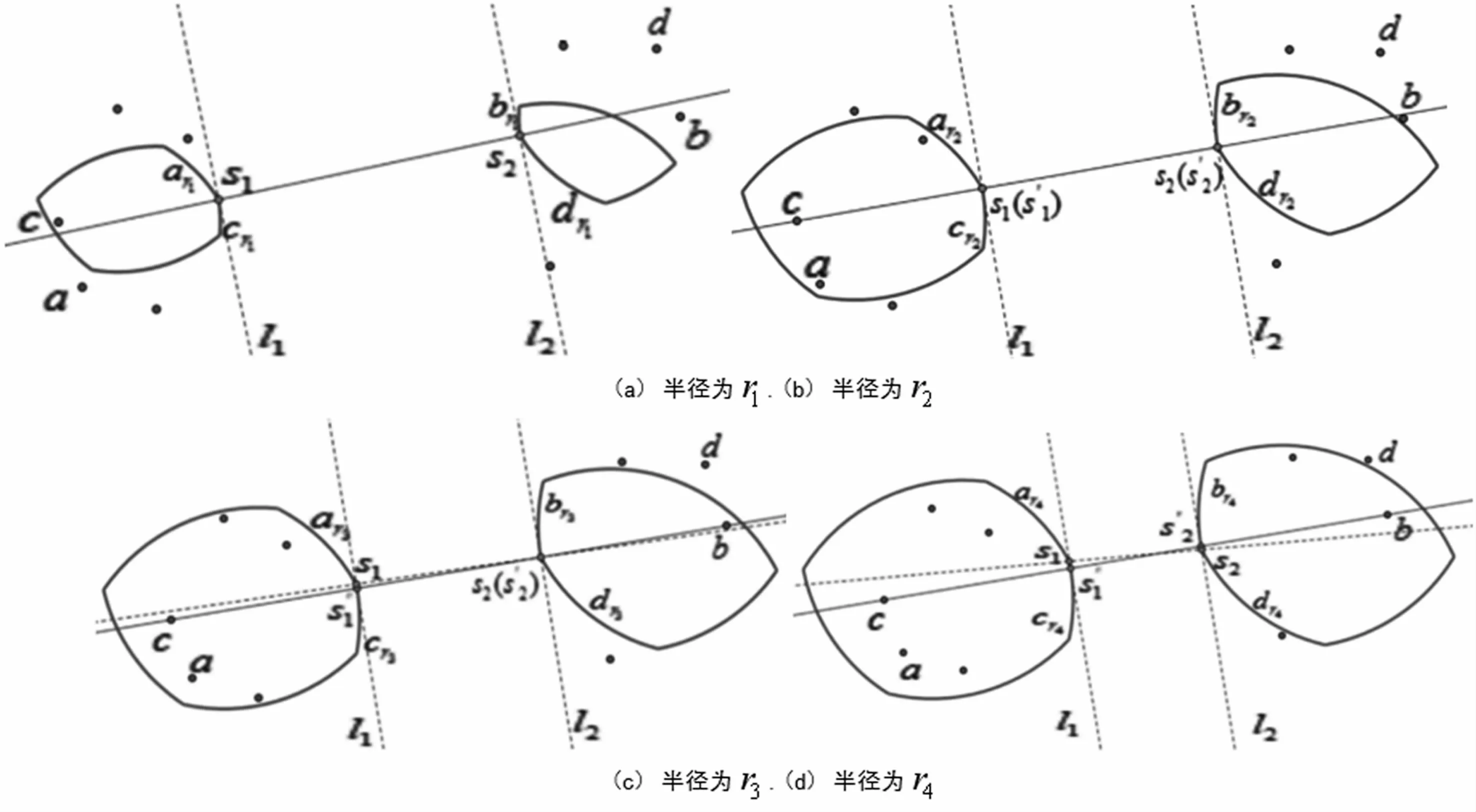
图7 引理6示例，r1＜r2＜r3＜r4，r2和r3为临界半径，当r＝r2时，l1与弧cr2相切；当r＝r3时，l2与弧br3相切；s1′在弧cr4上，s2′在弧br4上

4 算法设计与分析

这一节给出最小最大二点集覆盖问题的确定性算法设计并分析算法复杂性，具体算法流程见Algorithm 1。

算法第1行计算点集P1和P2的最小覆盖圆［18］，这部分可以在O（m+n）的时间内完成。

算法第2行到第3行，检查是否满足d（o1，o2）≤max｛r1，r2｝。如果是，则已然得到最优解。该检测可以在常数时间内完成。

算法第5行计算一个点到一个中心包的最近距离，这一步可以在O（log（m+n））的时间内求出［19］。

算法第6行到第7行，检查是否满足min｛d1，d2｝≤max｛r1，r2｝。如果是，则已然得到最优解。该检测同样可以在O（log（m+n））常数时间内完成。故第5行到7行总共可以在O（log（m+n））的时间内完成。

算法第9行到第12行，是在如果上述两种情况都不满足的情况下，第9行首先分别计算P1和P2的最远点Voronoi图，该过程可以在O（mlogm）和O（nlogn）的时间内完成。

算法第10行分别计算P1和P2的临界半径，这个过程可以在O（mlogm）和O（nlogn）的时间内完成。

算法第11行计算最优解区间，将这两个点集的所有临界半径合并排序，这可以在O（（m+n）log（m+n））的时间内完成；对每一个临界半径，可以在O（m+n）的时间内求出两个点集的中心包［3］，在O（log（m+n））的时间可以求出这两个中心包之间的最近距离［19］。因此，可以通过二分查找，在O（（m+n）log（m+n））的时间内找出一个包含最优半径的临界区间（rl，rh］。在该半径区间内，随着半径的变化两中心包的组合性质不会发生变化，同时满足当半径取rl时，中心包CHrl（P1）和CHrl（P2）之间的最近距离大于rl，当半径取rh时，中心包CHrh（P1）和CHrh（P2）之间的最近距离小于rh。

算法第12行求解最优圆心及半径，在文献［11］中，Huang等人给出求解最优半径需要通过并行计算的方法在O（log2（m+n））的时间内求解。由引理4、引理5和引理6可以设计算法并得出最优半径可以在常数时间内求解。当r∈（rl，rh］，两个中心包CHr（P1）和CHr（P2）变化过程中其组合性质不发生变化。记s1和s2是中心包CHrh（P1）和CHrh（P2）之间最近距离的控制点，这里分三种情况进行分析，其符号表示与上一节相同：

情况1若s1和s2分别是弧arh和弧crh，弧brh和弧d rh的交点。∀r∈（rl，rh］，一定满足CHr（P1）和CHr（P2）之间最近距离的控制点分别是弧ar和弧cr，弧br和弧d r的交点。因此只需要找到两个点满足这两点之间距离以及两点分别到｛a，c｝和｛b，d｝的距离全部相等，记这两个点为所求圆心即可。该计算在常数时间内即可完成。

情况2若s1和s2其中之一在弧上，不失一般性，假设s2在弧brh上。∀r∈（rl，rh］，CHr（P1）的控制点一定是弧ar和弧cr的交点，但是CHr（P2）的控制点有可能在弧br上，也可能是弧br和弧d r的交点。因此，需要通过5次计算：不仅需要找到两点满足两点之间距离以及两点分别到｛a，c｝和｛b，d｝的距离全部相等，还需要找到两点满足两点之间距离以及两点分别到｛a，c｝和b（｛a，c｝和d，a和｛b，d｝，c和｛b，d｝）的距离全部相等，在满足的结果中找出距离最小的两点作为圆心即可。

情况3若s1和s2均在弧上，不失一般性，假设s1和s2分别在弧ar和弧br上。∀r∈（rl，rh］，有如下几种可能：CHr（P1）和CHr（P2）的控制点可能在弧ar和弧br上；可能一个控制点在弧ar上，另一个为弧br和弧d r的交点；也可能一个控制点为弧ar和弧cr的交点，另一个在弧br上；或者一个控制点为弧ar和弧cr的交点，另一个为弧br和弧d r的交点。因此，需要通过7次计算：不仅需要找到两点满足两点之间距离以及两点分别到｛a，c｝和｛b，d｝的距离全部相等，还需要找到两点满足两点之间距离以及两点分别到｛a，c｝和b（｛a，c｝和d，a和｛b，d｝，c和｛b，d｝）的距离全部相等，以及线段la，d和lb，c的两个三等分点。接着检测计算出的两点到各自点集的最远点距离是否等于两点之间距离，最后在满足的结果中找出距离最小的两点作为圆心，因此在临界区间内找出最优半径可以在常数时间内完成。故算法第9行到到12行总共可以在O（（m+n）log（m+n））的时间内完成。

综上所述，可以得到：

定理给定分别包含m和n个点的两个平面点集P1和P2，最小最大二点集覆盖问题可以在O（（m+n）log（m+n））时间内求解。

5 结论与展望

本文考虑最小最大二点集覆盖问题并给出时间复杂性为O（（m+n）log（m+n））的确定时间算法，其中求解最优半径过程改进了Huang等人提出的并行算法。因为无论如何算法设计一定需要涉及排序这一操作［20］，而排序时间至少为O（（m+n）log（m+n）），因此本文设计的算法是目前为止最好的算法，并且不需要运用并行计算，大大减少了计算规模。而如果考虑两个圆覆盖一个含有n个点的点集情况，由于需要对点集进行分割，目前最好的算法仍然是Huang等人提出的O（n2logn）期望时间算法，而该问题的确定时间算法复杂性为O（n3logn）。因此，针对该问题，改进其算法的计算复杂性还是很有希望的。