产业转移下的海上丝绸之路沿线集装箱港口的投资决策研究
2020-09-27杨忠振陈东旭宫之光
杨忠振, 陈东旭, 宫之光
(宁波大学 海运学院,浙江 宁波315211)
0 引言
经济全球化导致产品的生产地与消费地严重分离,诱发大量的交通运输需求。过去30年随着中国世界工厂地位的确立,中国与欧美间的贸易量持续增加,围绕贸易货物在中国和欧美之间形成了世界级的海运主走廊,走廊两端出现了庞大的港航物流产业集群。目前,全球排名前20的港口中10个在中国,5个在欧洲或北美。但是,在主航线中间地带由于既无大的制造业集群也没有大规模消费地,因此港口规模与地位都无法与两端的相提并论。例如,MSR沿线只有5个港口排名世界前20,其新加坡港、巴生港和丹戎帕拉帕斯港均是借助中转功能才奠定的世界级港口的地位。
上述现象正在或即将发生变化,由于劳动力和土地成本的增加,中国的区位优势逐渐下降,相当数量的制造业开始向其他区位优势明显的区域转移。由于海上丝绸之路沿线工资水平普遍低于中国,部分地区甚至仅为中国的14.8%,因此MSR沿线国家有望成为新的全球制造业基地,他们与其他国家的贸易将逐渐增多,原本的地区性港口很难满足新的需求,MSR沿线港口能力不足将成为制约其制造业发展的瓶颈。由于货物运输需求与港口供给之间存在着“鸡-蛋”的互动关系,因此MSR沿线有必要增加港口供给,以在满足运输需求的同时,改善可达性,提升区位优势,促进制造业的进一步转移。
很显然互为因果的“鸡-蛋”的正向反馈存在上界,例如:增加港口供给可促进制造业发展,增加劳动力和土地的需求,导致工资和地价升高,最终使得承接产业转移的优势逐渐走低。因此,港口规模对制造业转移规模的边际效益是递减的,当港口投资的边际收入无法覆盖边际成本时,港口投资会出现负收益。反过来,制造业的持续增加也会导致港口运输需求超出土地和岸线资源、生态环境以及末端运输的能力的上限。
因此,分析制造业向MSR沿线的转移趋势,明确沿线地区港口需求与供给间的均衡状态,优化沿线港口的投资,实现港口利益最大化,成为MSR沿线向新的世界级制造中心演变过程中关键问题。由于港口投资与产业转移之间具有主从式逻辑关系,因此可用双层规划予以描述。其中,港口投资是领导者,在上层决定着港口的服务水平,进而影响制造业向港口腹地转移的规模;制造业转移是跟随者,在下层选择生产地点和运输路径。分析上下层之间的反馈关系,可明确不同港口投资方案下的产业转移状况,得到集装箱港口投资的优化方案。
1 文献回顾
有关港口投资的研究主要有三类:1)投资规模优化,涉及优化方法、算法及影响因素分析;2)港口规模与母城经济间的关系研究,涉及单位港口规模对母城经济的影响;3)港口投资方案评价,涉及港口投资的可行性。
在第一类研究中,Dan[1]以投资金额、在港时间与内陆运输成本之和最小为目标,建立港口投资与定价模型。Meersman[2]研究了港口竞争、港口交通波动性等不确定因素对投资的影响。Demirci[3]考虑装卸车环节对港口能力的影响,用仿真的方法研究港口投资。黎继子等[4]将遗传算法与神经网络相结合,建立投资决策模型,提高了模型求解的收敛速度。李和忠等[5]和Kuang等[6]关注港口效率,借助扩张型实物期权描述投资决策的柔性价值,实现港口多阶段投资的有效整合。Allahviranloo等[7]建立考虑投资成本、货物运输网络等约束的模糊整数规划模型。匡海波等[8~10]借助动态规划和随机规划,建立考虑港口效率及生态承载率的多期投资优化模型。Musso等[11]指出港口规模过小将增加拥堵成本,过大会增加操作成本,并以最小化总成本为目标构建优化模型。尽管此类研究为港口投资决策提供了方法,但对产业转移下的港口投资问题缺乏针对性。
在第二类研究中,张燕等[12]用格兰杰检验和VAR动态分析,验证港口与区域经济间的因果关系。郭秀娟[13]、申勇锋等[14]、姜超雁等[15~17]和叶宜丹[18]基于投入产出法测算港口规模对区域GDP、就业 等 的 贡 献。杨 家 其 等[19]、高 琴 等[20]依据科布-道格拉斯生产函数测算吞吐量对腹地经济的贡献。此类研究解释了港口规模和区域经济、劳动力需求之间的逻辑及数量关系,是港口投资优化的基础。在第三类研究中,李新然等[21]建立了基于RBF神经网络的港口投资效益预警模型,并验证了模型预测的准确性。Han等[22]考虑国家风险、基础设施水平等,评价跨国港口投资方案。这两类成果是港口投资优化的前提,本文将投资回报率作为约束条件,以提高港口投资优化方法的实用性。
2 问题描述
MSR沿线港口投资与产业转移之间存在图1所示的正反馈关系,即投资港口可提高港口能力(①),减少货物通过港口的阻抗,同时影响港口腹地的工资水平和土地成本(②)。而制造业基于港口阻抗、劳动力和土地成本转移(③),转移规模决定着港口需求、劳动力需求及经济水平(④),进而反作用于港口阻抗、劳动力和土地成本(⑤)。
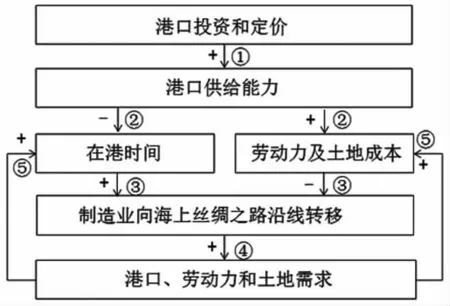
图1 产业转移背景下港口投资双层决策问题的逻辑关系
产业转移是企业个体再选址行为的宏观体现,为研究港口投资对产业转移的影响,可把制造业看作是以年产值为单位的连续个体。假设货物销售价格不变,则个体企业以广义成本(生产+运输成本)最小为目标再选址生产。此时,产品生产+运输过程类似于交通运输需求在运输网络上由出发地移动到目的地的过程。例如,图2为由2个产地(1和2)和3个消费地(j’)构成的网络。不考虑产业转移时,可将生产+运输各环节抽象成具有不同同行阻抗的路段。其中,路段集合A1代表生产环节,阻抗包括土地成本、劳动力工资和税收;路段集合A2代表生产侧的内陆运输环节,阻抗包括运输费用和运输时间;路段集合A3代表在港环节,阻抗包括港口收费和在港时间;路段集合A4代表海上运输环节,阻抗包括海运费用和时间;路段集合A5代表消费侧的港口卸船环节和内陆运输环节,阻抗包括港口使费、在港时间和内陆运输成本。假设消费地的需求不变,则A5路段的阻抗为常数,决策时可忽略。

图2 无产业转移时的生产+运输网络
如果区域2有区位优势,则区域1的产业将向区域2转移。为描述这种转移,在网络中增加虚拟路段A0(图3中虚线箭头)。如果不考虑搬迁成本,可设A0的阻抗为0。用A表示所有的路段集合,则A=A0+A1+A2+A3+A4+A5。除路段外,网络中的节点有:起点i∈I,对应的虚拟节点i′∈I′;产业转出地的港口p∈P1,对应的虚拟节点;投 资 的 港 口p∈P2,对 应 的 虚 拟 节 点,P=P1∪,卸船港口j∈J。基于该网络可分析制造产业转移前后,贸易货物在空间上流向流量的变化,以及在多式联运网络中的路径选择行为,分析港口投资对产业转移的服务与促进作用,以及投资港口可获得的利益。
3 数学模型
3.1 基本假设
S1:全球市场对产品的需求不变;
S2:不考虑制造企业搬迁成本;
S3:其他港口的装卸费率不变;
S4:其他港口腹地的土地及劳动力成本不变;
S5:销往国际市场的产品均经由港口运输;
S6:海运和陆运的运输费率不变;
S7:不考虑资金的时间价值。

图3 有产业转移时的生产+运输网络图
3.2 模型结构
上层模型

式(1)表示港口收益最大;式(2)为投资回报率约束;式(3)为港口规模约束;式(4)为码头数量的非负整数约束;式(5)为投资额和泊位量之间的关系式;式(6)为港口使费定价约束。
下层模型

其中:tca:路段a阻抗;fijk:OD(i,j)间路径k的流量;qij:OD(i,j)间的总流量;xa:路段a上的流量;δ:0-1变量;tpi:产地i的税收;pv:单位集装箱产品的货值(美元/TEU);hpi:产地i的工资(美元/人/天);nh:制造1 TEU产品所需的劳动力数量;lpi:产地i的土地成本(美元/平方米);ns:制造1 TEU产品所需的土地面积;ωip:产品由产地i到港口p的公路分担率;frroad,frrailway:分别为公路运费率和铁路运费率(美元/公里/TEU);fbrailway:铁路运费基准价(元/TEU);α:货物的时间价值;t0:路段a自由流时的同行阻抗(a∈A3);β1,β2,β3:待估参数;分别为产地i到港口p的公路和铁路运距;vroad,vrailway:分别为公路和铁路的运行时速:港口p′到港口j的海运费率;vshipping:集装箱船的航速港口p′到 港 口j的 航 行距离;GDPi:投资后节点i的GDP;κ:边际消费倾向,即增加1美元国民收入中用于最终消费的数量;ρ:GDP对地价的影响系数没有港口投资时地区i的工资水平地区i的劳动力供给总量;:没有港口投资时,地区i的劳动力需求量;υ:单位港口投资诱增的就业需求。
式(7)为下层模型的目标函数;式(8)~(10)为流量约束,保证货物流量非负且守恒;式(11)为阻抗函数;式(12)为0-1变量;式(13)为GDP函数,与港口投资和制造业转移相关;式(14)为地价函数,由港口投资后的GDP决定;式(15)为工资函数,根据刘易斯拐点可知,当劳动力从过剩走向短缺为转折点工资开始上升。
4 案例分析
MSR途径东盟十国、南亚四国、肯尼亚、沙特阿拉伯、埃及、苏丹等,约65%的沿线国家具有承接制造业的可能,但当地的港口能力制约着制造业的发展。斯里兰卡斯政府一直拟通过发展科伦坡港区位国家的优势,促进制造产业向斯转移。这里选取科伦坡港为研究对象,在制造业向斯转移的情况下,优化科伦坡港集装箱码头的投资与定价。
4.1 使用数据
根据中国商务部等部门联合发布的《对外投资合作国别地区指南-2014版》得到斯里兰卡的几项数据如表1所示。

表1 斯里兰卡的几项数据指标
将世界贸易按洲际板块分成6个区域,即欧洲、亚洲、北美洲、南美洲、大洋洲和非洲。分别选取各区域内最大的港口作为卸货港,即鹿特丹港、上海港、洛杉矶港、里约热内卢港、悉尼港、亚历山大港。中国和斯里兰卡到各区域的货物价值如表2所示。

表2 中国和斯里兰卡与世界各地间贸易分布 (单位:亿美元/年)
4.1 求解结果及分析
把上层模型的目标函数值作为适应度值,用遗传算法求解双层模型。有计算结果可知,考虑制造业转移时,科伦坡港应投资新建8个集装箱泊位,码头费率应为111美元/TEU。此时,港口新增收益0.73亿美元/年,投资回报率为7.30%,高于4.5%的银行贷款收益率。在该方案下,斯里兰卡的年GDP增加值由788.24亿美元上升到1106.59亿美元,增长40.39%,制造业工人的工资由420美元/月增长到625美元/月。可见港口投资对斯里兰卡的宏观经济和居民收入均有正向刺激作用。
在优化的港口投资和费率下,斯里兰卡出口到其他区域的货量如图4所示,出口货值由149.6亿美元/年增长到462.7亿美元/年,增长209%。可以说每年增加的313.1亿美元的出口货物就是中国向斯里兰卡转移的制造业的年生产值,因此投资港口可明显地促进制造业向MSR沿线转移。投资建设科伦坡港后,中国出口到各区域的货物都有所减少,但比例并不明显(如图5),这是因为中国制造业出口总量大,转移的只是小部分。

图4 不同港口规模下斯里兰卡到各地的出口量对比

图5 中国到各区域出口货值的变化
为分析新增泊位对港口收益的影响,分别计算不同投资规模所对应的港口的边际收益和累计新增收益,如图6所示。可以看出,边际收益随新增泊位先升后降,当新建8个以上泊位时,投资的边际收益为负。由于新增收益等于其腹地承接的制造业的出口运输成本与港口投资及维护成本的差值,因此可通过港口投资规模对产业转移的影响,来进解释新增泊位对港口收益的影响。
新增泊位数对产业转移等的影响如图7所示,其中,累计产业转移货值与新增泊位数正相关(图7中虚线),新增1~4个泊位时,上升速率接近常数;新增4个以上泊位时,上升速率降低;新增8个以上泊位时,上升速率趋近于0。这是由于新增4个以下泊位时,劳动力供大于求,工资不随产业转移而上升(图7中圆点折线),土地成本上升幅度较小(图7中方形折线),港口成本变化幅度较小,即港口需求与供给能力的比值接近定值,新增泊位所诱增的边际产业转移货值相对固定;新增4个以上泊位后,劳动力从过剩走向短缺,工资上升,土地成本上升,港口成本相应上升,因此边际产业转移货值逐渐降低;当投资新建8个以上泊位时,单位港口投资所诱增的产业转移量进一步下降,趋近于0,额外的港口投资所诱增的营业收入不足以覆盖投资成本,因此在该阶段累计收益呈递减趋势(图7中的曲线)。
随着投资的进一步增加(如,新建10个泊位),港口所在地的生产+运输成本与中国的持平,斯里兰卡无法通过港口投资吸引制造业,科伦坡港对制造业发展的抑制作用消失,由新增码头和诱增的制造业所导致的高工资和高地价成为腹地发展制造业的新瓶颈。

图6 港口新增收益随投资规模变化的情况
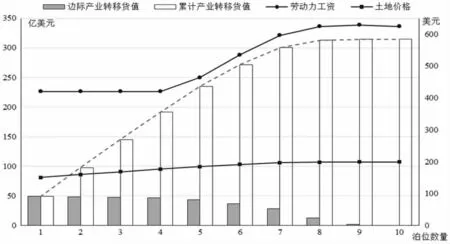
图7 产业转移量、工资、地价随投资规模的变动情况
5 结论
本文构建了考虑产业转移的港口投资规模与定价优化模型,结合港口投资对区域工资水平及地价的影响,基于产业在再选址过程中追求总成本最小的用户平衡原理,将产品的生产+运输环节类比成运输需求从出发地到目的地的移动过程。在虚拟的超级网络上,描述产业转移的过程,通过港口投资与产业转移行为间的相互反馈,分析港口投资与产业转移之间的相互影响关系,得到最优的港口投资方案与港口使费标准。
为验证模型,以科伦坡港集装箱码头投资为例进行数值分析,结果表明产业转移规模与港口投资规模正相关,但由于新增港口规模和产业规模会导致工资上涨和土地溢价,当劳动力+土地成本与中国持平时,科伦坡港的投资对产业转移的影响到达上界,腹地的产业规模不再随港口投资的增加而增大。另外,一定范围内港口投资收益与港口投资规模之间亦在正相关,且同样存在上界。因此,对港口投资者而言,合理把握港口供给与港口需求之间的正反馈关系及其上界,找出港口收益曲线的拐点,是最大化港口投资收益的关键。
