多级荷载下弱膨胀土的膨胀变形特性试验研究

边加敏

(南京交通职业技术学院路桥工程学院，江苏 南京 211188)

膨胀土是一种特殊的黏性土，富含亲水性矿物成份，具有典型的膨胀性、超固结性和裂隙性的特征，土体强度及变形性能随着含水率变化而变化的性质十分显著。由于土体浸水而导致土体强度降低、变形增大，进而导致建筑物破坏，被誉为工程建设中的“癌症”，对膨胀土膨胀性能的研究是当前的热点与难点。当前对于膨胀土的膨胀性能主要通过相关变形指标评判，如土体的标准吸湿含水率、线膨胀率、膨胀力、自由膨胀率及小于0.002 mm颗粒的含量等。

当前对膨胀变形量(线膨胀率、膨胀力等)的研究集中于初始状态(初始含水率、初始干密度及上覆压力)对膨胀变形的影响。众多学者建立了多种不同初始状态下膨胀变形量预估模型，预估不同初始状态下的膨胀变形量[1-4]，在此基础上有学者[5-6]采用所建立的膨胀变形预估模型，对用于路堤填筑的膨胀土路堤的总变形量进行了预估，Nelson 等[7-8]基于压缩试验及常体积膨胀力试验提出了预测自由膨胀量的方法；Rao等[9]提出了一个能预测均质膨胀土层的最终膨胀量的近似解。韦秉旭等[10]、侯超群等[11]研究了膨胀土表面裂隙规律与强度关系。这些研究成果对于膨胀土用于路堤填筑的工程应用起到十分重要的推动作用，有一定的工程意义。

但目前研究还存在一定的问题，主要表现在以下几个方面。其一，部分变形指标的试验方法不统一，造成膨胀数值的可比性不强，如多级荷载下的线膨胀率试验，由于土工试验规程中采用“需要时也可以分级卸载的方式”的表述，工程技术人员对于多级荷载下线膨胀率测定，常见试验方法有2种：①制作一种试样，在一定的荷载下固结稳定后加水膨胀至变形稳定，并逐级卸载至相应的荷载，并测定土体的膨胀量；②制作若干“等同”试样，逐个加载固结稳定浸水饱和后测定土体的膨胀变形量。同样对于膨胀力的测定值也存在相同的问题：①美国规范ASTMD4546-16方法；②我国土工试验规程的平衡加载法。两种试验方法均有学者采用。其二，有学者[5-6]提出了多种不同初始状态下膨胀变形量的预估模型，但各初始状态的相互耦合作用不强，各初始状态对于膨胀变形量影响的相互联系较弱，部分影响因素通过乘法[7]的方式进行考虑。其三，现行试验方法常采用控制土样高度的方法对变形量进行研究，由于土体浸水膨胀或压缩变形的大小主要是由土体的基本性质决定，相比较于采用试样高度研究土体的变形量，采用孔隙比更能反映出土体浸水膨胀与压缩的根本特性。

基于此，本文以高淳某边坡弱膨胀土为研究对象，进行了不同初始含水率及初始干密度下土体在多级荷载作用下的固结及浸水膨胀变形试验，研究了试验土体的孔隙比与初始含水率、初始干密度及上覆压力的关系，并借此提出土体膨胀变形量的计算公式，将其应用于路堤膨胀变形量的计算中。

1 试验土样及试验方法

1.1 试验土样

试验土样取自南京高淳某边坡，取土深度在0.8～1 m之间，按照文献[12]的试验方法进行土性参数试验，测得土体的液限为54%，塑限为27%，塑性指数为27，自由膨胀率为50.4%，最大干密度为1.83 g/cm3,最优含水率16.5%，土粒的比重为2.74，土体小于0.002 mm颗粒的含量为31.5%，判定土样为高液限弱膨胀土。

1.2 试验土样的初始状态及试验方法

(1)土样初始状态

将土样分别配制成初始含水率为16.5%和19.5%，将每种初始含水率土体采用静压的方式分别压制初始干密度为1.60，1.65，1.70和1.75 g/cm3。

(2)试验方法

将边坡中取出的土样晾干后破碎过2 mm孔径筛，测定土体的含水率，分别加水至预设含水率，拌合均匀后放入塑料袋中扎紧并放置24 h，使得水分分布均匀，分别按照设定的初始状态压制直径为61.8 mm、高度为20 mm的小环刀样。

将压制好的小环刀样装入固结仪中，预加2 kPa的上覆压力，使试样与土体充分接触稳定，将百分表安装于固结仪上，调整百分表初始读数为整数，分别按照12.5，50，75，100，150，200和300 kPa的顺序逐级加载，分别读出各级荷载作用下土体固结稳定后的读数，直至在300 kPa荷载下固结稳定，读出百分表读数后，计算各级荷载作用下试样的高度，加水至膨胀稳定后，读出百分表读数，计算试样高度，再按照300，200，150，100，75，50，25和12.5 kPa的荷载顺序逐级卸载，待变形稳定后分别读出百分表读数，计算不同荷载作用下浸水饱和后的土样高度。当膨胀或固结变形量小于0.01 mm/h时，认为土样变形稳定。

将试验过程中试样的高度变化按照式(1)计算土体的孔隙比：

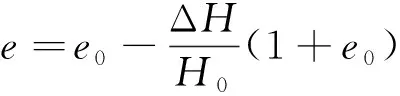
(1)

式中：e0——土体初始孔隙比；

ΔH——试验过程中试样高度变化；

H0——土体初始高度。

2 试验数据分析

2.1 固结与膨胀变形曲线分析

图1为初始干密度为1.60，1.65，1.70及 1.75 g/cm3的4种土样分别在12.5，25，50，75，100，150，200和300 kPa共8种上覆压力下固结及浸水膨胀变形后土体孔隙比与上覆压力之间的关系。

通过比较图1中8种初始状态土体的固结及浸水膨胀变形过程，可见浸水膨胀及固结过程均表现出相似的变形特征，土体浸水膨胀及固结过程的孔隙比均随着上覆压力的增大而逐渐减小。而在同一初始状态下，固结及浸水膨胀变形后的孔隙比也均随着上覆压力的增大而逐渐减小，膨胀变形的上覆压力与孔隙比关系曲线的斜率明显大于固结曲线。

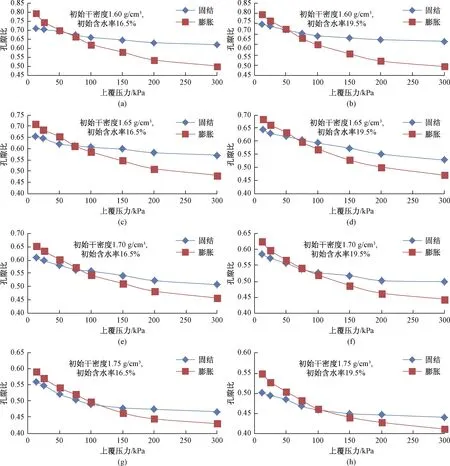
图1 不同初始干密度和初始含水率时上覆压力与孔隙比关系Fig.1 Relationship between the overlying press and void ratio of different initial dry densities and initial water contents

同时，固结与膨胀两种变形曲线在本文试验状态下均存在交叉点，此交叉点表示在特定上覆压力下膨胀土土体在固结及浸水膨胀变形过程中的孔隙比相同，表明土体浸水饱和后，既不发生膨胀变形也不发生压缩变形。

影响土体浸水后的膨胀与压缩变形特征的主要因素有土体的颗粒级配、饱和度、应力状态及土体的基本特性等。当外部条件稳定时，土体颗粒表面负孔隙水压力和表面张力的存在使得土体处于稳定状态，加载时土体颗粒内部孔隙减少水分流出，土体内部的负孔隙水压力与表面张力发生了重组，从而导致颗粒发生相对滑动，土体颗粒的相对滑动及水分的排出是土体固结变形的主要原因。而膨胀土发生浸水膨胀主要是由于土体内部存在大量的亲水性矿物成分如蒙脱石等，当土体浸水后，水分子进入由范德华力连接的蒙脱石晶格内部，使得分子间的间距变大，造成了土体的膨胀变形，当这种膨胀变形受到约束时产生了膨胀力，当外部的上覆压力小于膨胀力时产生膨胀变形，反之则产生压缩变形。

将图1中8种初始状态土体的上覆压力与孔隙比典型曲线的关系图简化后绘于图2中。

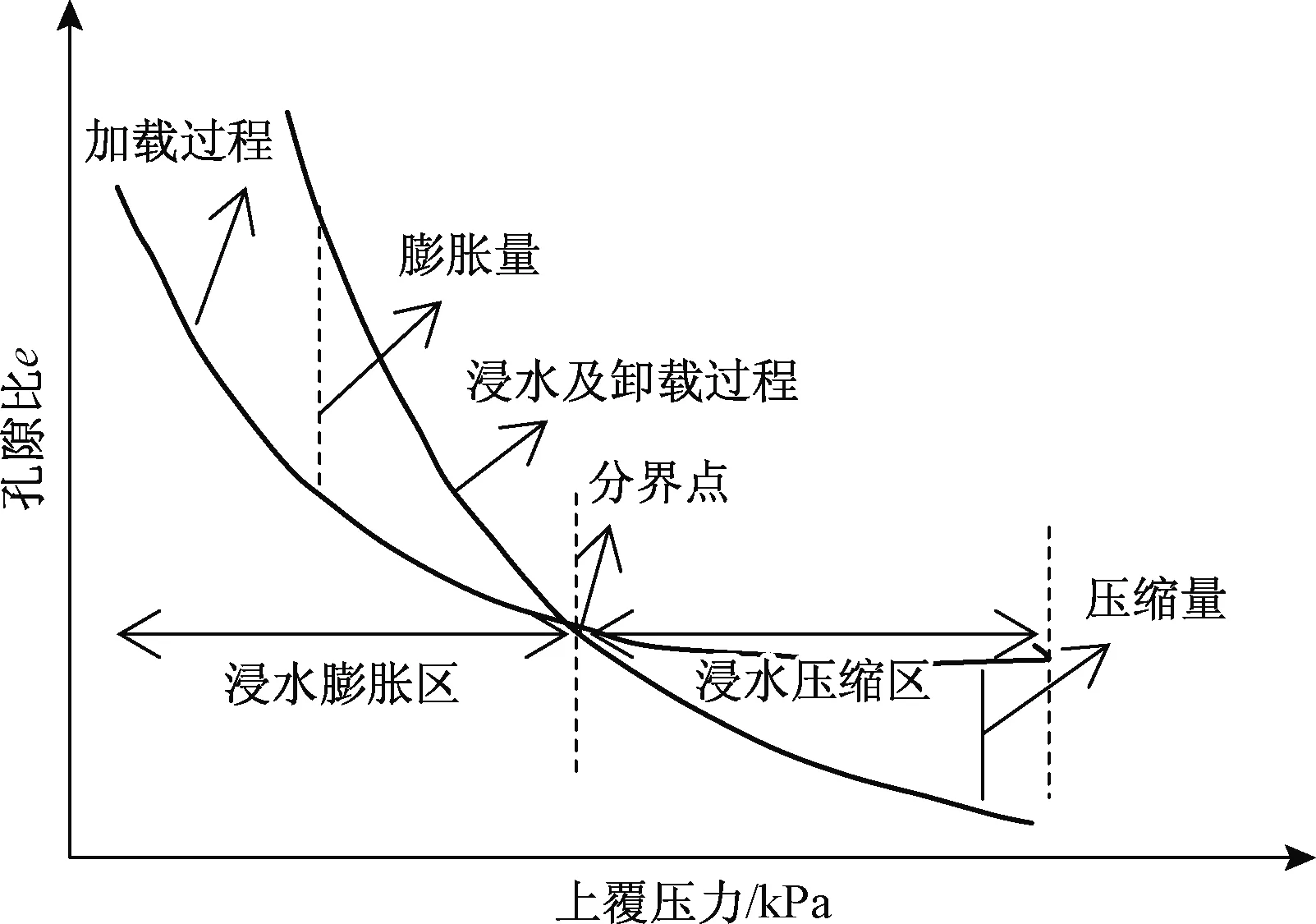
图2 土体浸水膨胀与压缩典型图Fig.2 Typical diagram of expansive and consolidation

由图2可见，在上覆压力较小时土体浸水饱和后呈现明显的膨胀变形特性，而在上覆压力较大下浸水饱和时呈现明显的压缩变形特性，在图2中表现为在上覆压力较小的前段曲线中(分界点之前)膨胀曲线在固结曲线的上方，这表明土体浸水饱和后的试样高度大于土体固结稳定后的高度，表明土体浸水饱和后处于膨胀变形状态。而在曲线分界点的后段，固结曲线在膨胀曲线之上，土体浸水饱和后的试样高度比固结稳定后的高度低，表明土体浸水饱和后处于压缩状态。

结合图1可看出，8种初始状态土体在交点前后所对应的固结与膨胀曲线特征基本类似，在分界点之前，随着上覆压力的增大，2种曲线之间的孔隙比差值逐渐减小，这表明，随着上覆压力的增大土体的膨胀变形量逐渐减小。而在分界点之后，随着上覆压力的增大，2种曲线孔隙比的差值逐渐增大，表明浸水后土体的压缩变形量随着上覆压力的增大而逐渐增大。

2.2 膨胀变形曲线分析

为分析膨胀稳定后的孔隙比与上覆压力的关系，将不同初始状态土体浸水饱和后的孔隙比与上覆压力的关系列于图3中。

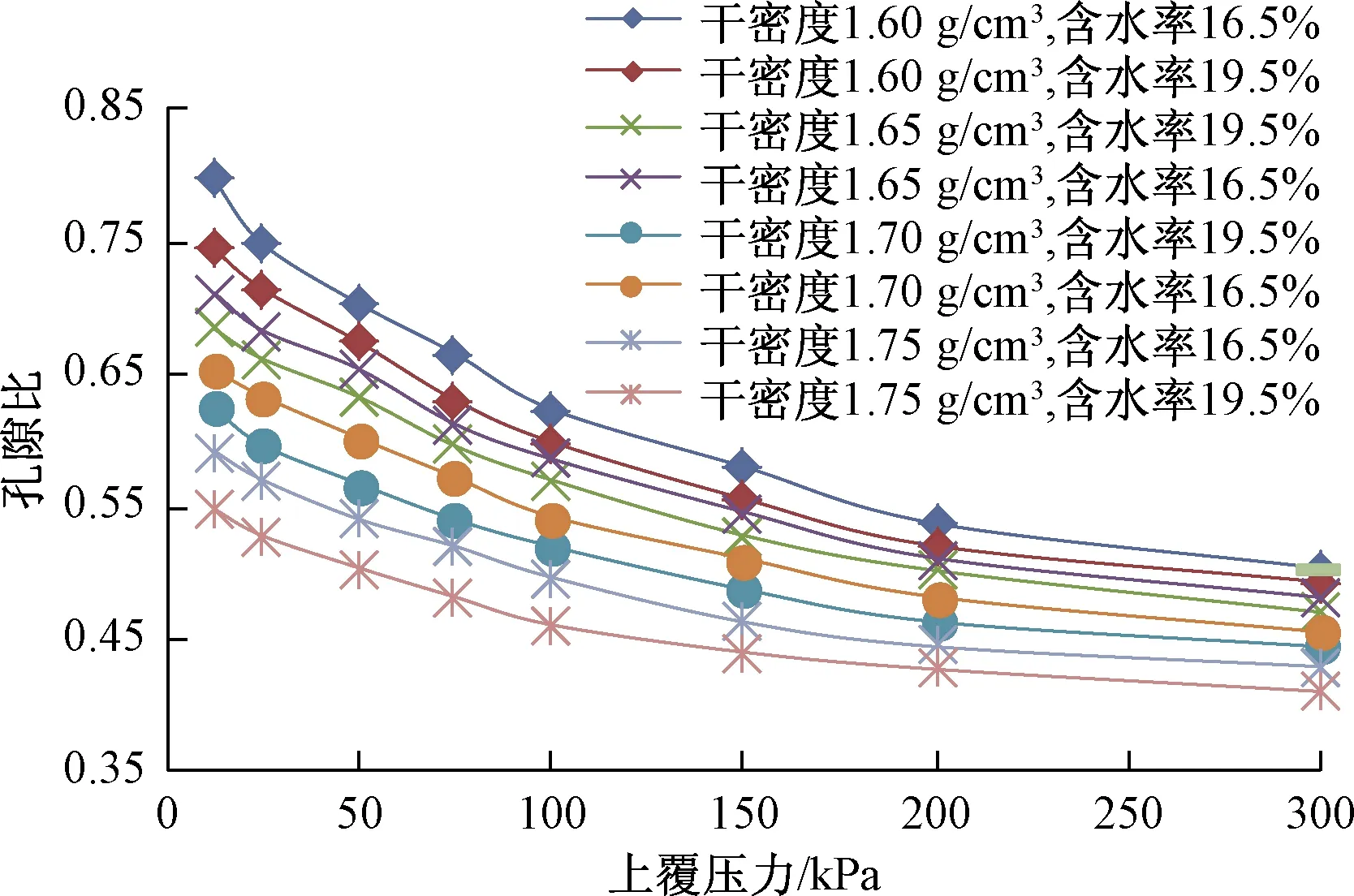
图3 上覆压力与孔隙比的关系Fig.3 Relationship between the overlying press and void ratio

由图3可以看出：

(1)土体浸水膨胀稳定后，不同的初始状态下的孔隙比差值随着上覆压力的增大而逐渐减小，膨胀变形曲线随着上覆压力的增加逐渐接近，这表明不同初始状态下土体浸水饱和后的孔隙比可能在某一特定的上覆压力下达到稳定，并逐渐趋于一致。关于这一现象产生的深层次的原因及机制，还有待进一步研究揭示。

土体变形稳定后的孔隙比主要取决于上覆压力、初始状态及土质土性等，土体的初始状态及土质土性等主要决定约束土体变形所需上覆压力的大小。浸水膨胀稳定后，土体最终所达到的状态主要由约束膨胀变形所需的力及上覆压力两种力的相对大小决定。当上覆压力小于约束膨胀变形所需的力时，上覆压力不足以约束土体变形，土体表现为膨胀变形状态。当上覆压力大于约束膨胀变形所需的力时，土体表现为浸水压缩。而压缩量的大小实际取决于上覆压力及约束膨胀变形两种力的相对大小。当上覆压力远远大于膨胀力时，土体的最终孔隙比实际主要由上覆压力决定。而在较大的压力下固结稳定时，固结稳定后的孔隙比主要受土体颗粒的负孔隙水压力及表面张力的相对变化引起，在较大的上覆压力下，土体颗粒的负孔隙水压力及表面张力的稳定值的主要影响因素是土体的性质，如：土体颗粒大小及分布、蒙脱石的含量等，外部因素对其影响相对较小，这可能是造成在较大上覆压力下土体孔隙比随着上覆压力的增大而逐渐趋于一致的原因。

(2)在相同的初始状态下，浸水饱和后土体的孔隙比随着上覆压力的增大而逐渐减小，相互之间的关系可采用式(2)拟合：

ep=klnp+b

(2)

式中：ep——压力p下浸水饱和稳定后的孔隙比；

k，b——拟合系数。

将拟合系数k，b列于表1中。

表1 不同初始状态下拟合参数k及b值

(3)比较4种不同初始状态下土体的膨胀变形曲线，可见初始干密度及初始含水率对于浸水的变形量均存在一定的影响。对于相同初始干密度的土体，初始含水率越大，浸水膨胀稳定后的孔隙比越小，表明土体的初始含水率对土体膨胀区膨胀变形量及压缩区的压缩变形量均存在一定的影响。初始含水率相同而初始干密度不同的土体，在相同的上覆压力下，初始干密度越大，浸水膨胀稳定后的孔隙比越低，表明初始干密度对于土体的膨胀稳定后的孔隙比存在一定的影响。

2.3 土体膨胀与压缩分界点分析

将2种初始含水率土体的膨胀与压缩变形分界点的上覆压力与孔隙比关系绘于图4中。

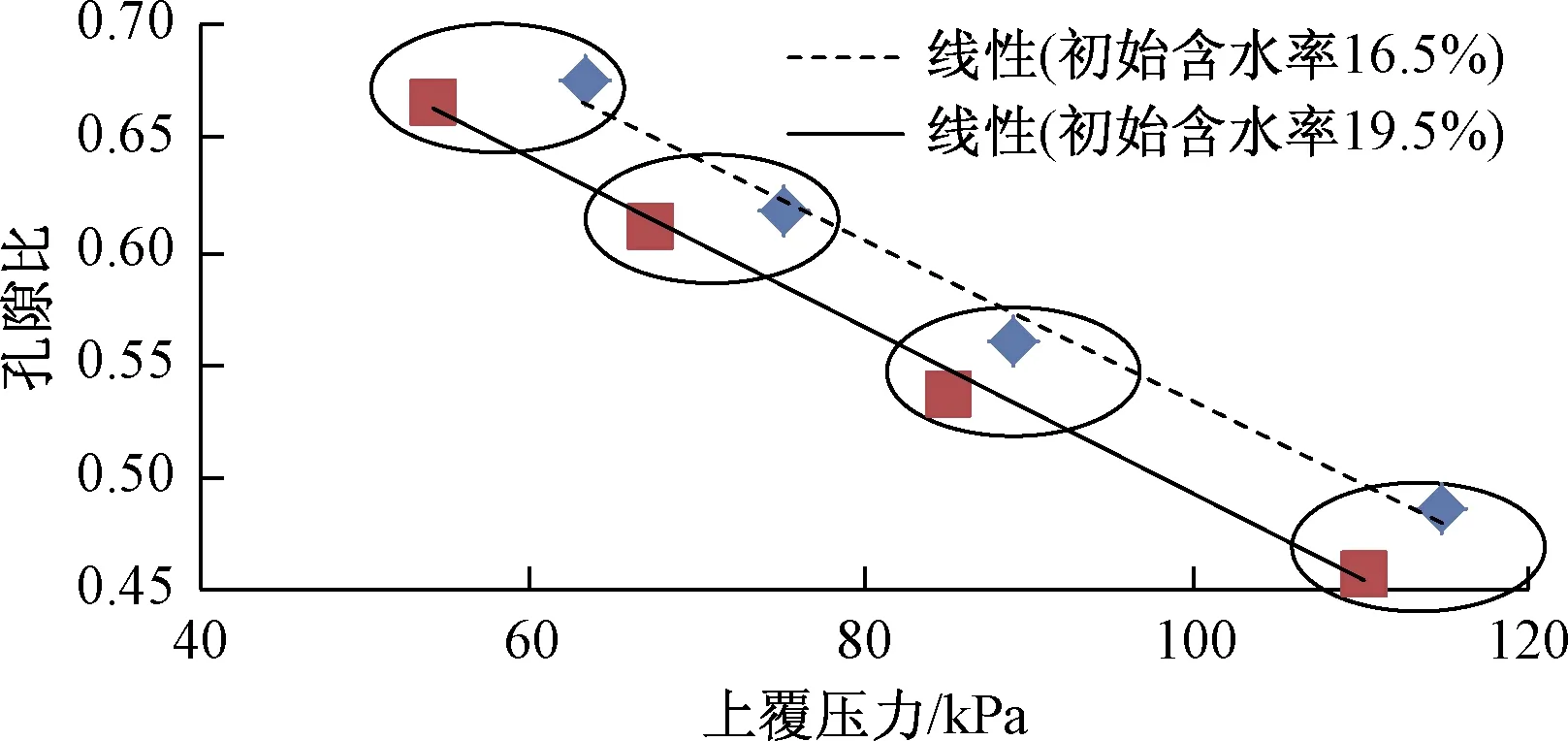
图4 分界点上覆压力与分界点孔隙比关系Fig.4 Relationship between the boundary point overlying press and boundary point void ratio

由图4可见，比较同一初始干密度下2种初始含水率的上覆压力可知(图中圈中的点)，初始含水率越大，分界点的上覆压力越小，这说明在相同的初始干密度下，初始含水率越大，土体浸水后维持土体孔隙比不变所需的上覆压力越小。而浸水稳定后，2种初始含水率土体分界点的孔隙比略有变化，且不呈现明显的规律性。对于相同初始含水率的土体，分界点的孔隙比随着上覆压力的增大而减小，这表明在相同的初始含水率下，初始干密度越大的土体，分界点的孔隙比越小，这主要是由于在相同的含水率下土体初始干密度越大、土体颗粒含量越多、平衡稳定时的孔隙越少所造成的。

图5为2种初始含水率土体的分界点上覆压力与初始干密度的关系。

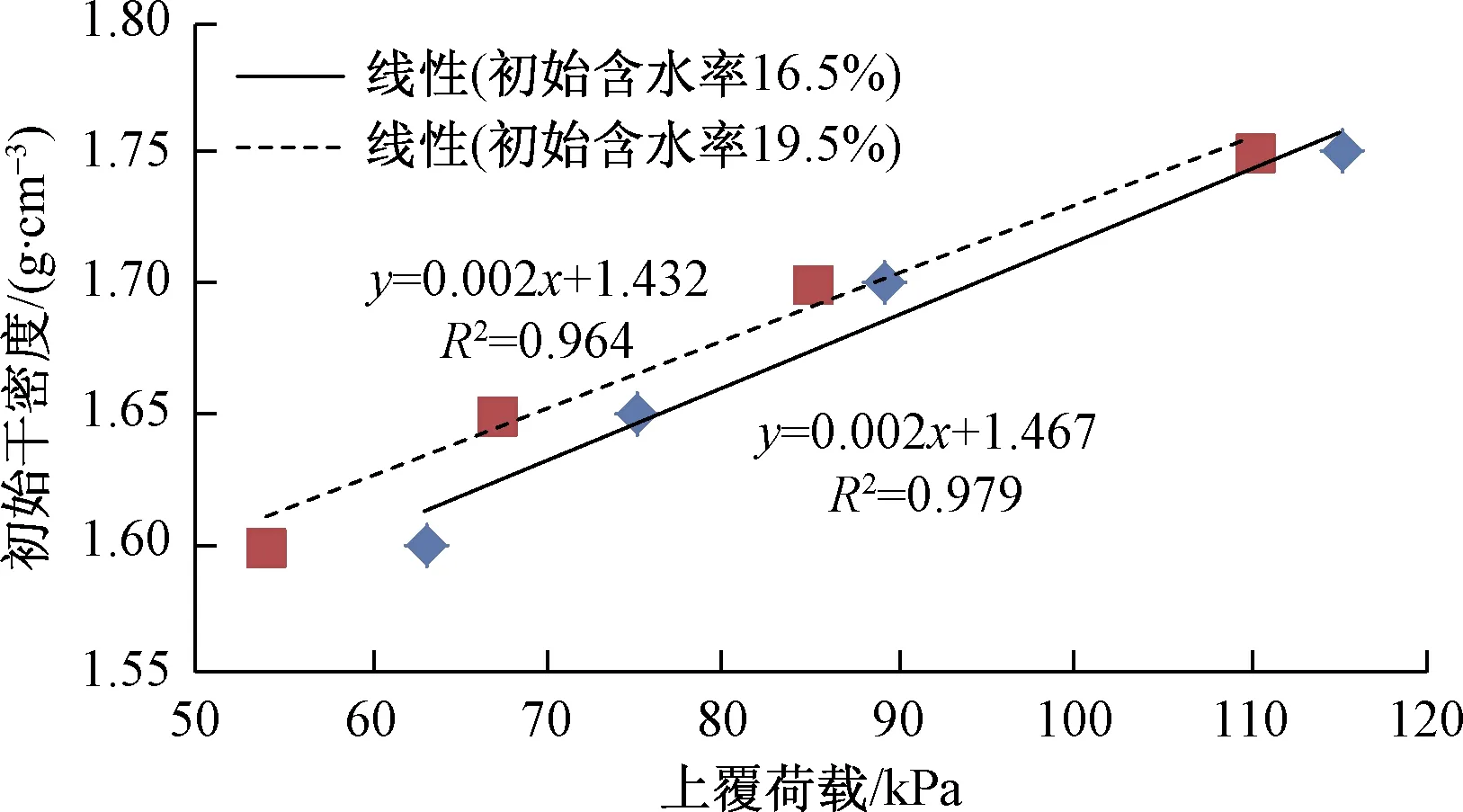
图5 初始干密度对分界点上覆压力的影响Fig.5 Initial dry density effect on the boundary point overlying press

分析图5中相同初始含水率土体的上覆压力可知，土体的初始干密度越大，分界点的上覆压力越大，表明初始干密度越大的土体，浸水后饱和后维持土体膨胀稳定所需的上覆压力越大，2种含水率不同曲线分界点初始干密度与上覆压力关近似呈线性关系：

ρd0=a1Pf+b1

(3)

式中：a1，b1——系数，与初始含水率有关；

ρd0——土体的初始干密度；

Pf——分界点上覆压力。

2.4 土体膨胀区试验数据分析

图6为2种初始含水率土体在1.60，1.65，1.70和1.75 g/cm3共4种初始干密度下，浸水膨胀稳定后土体在膨胀区的上覆压力与膨胀稳定后孔隙比关系曲线。

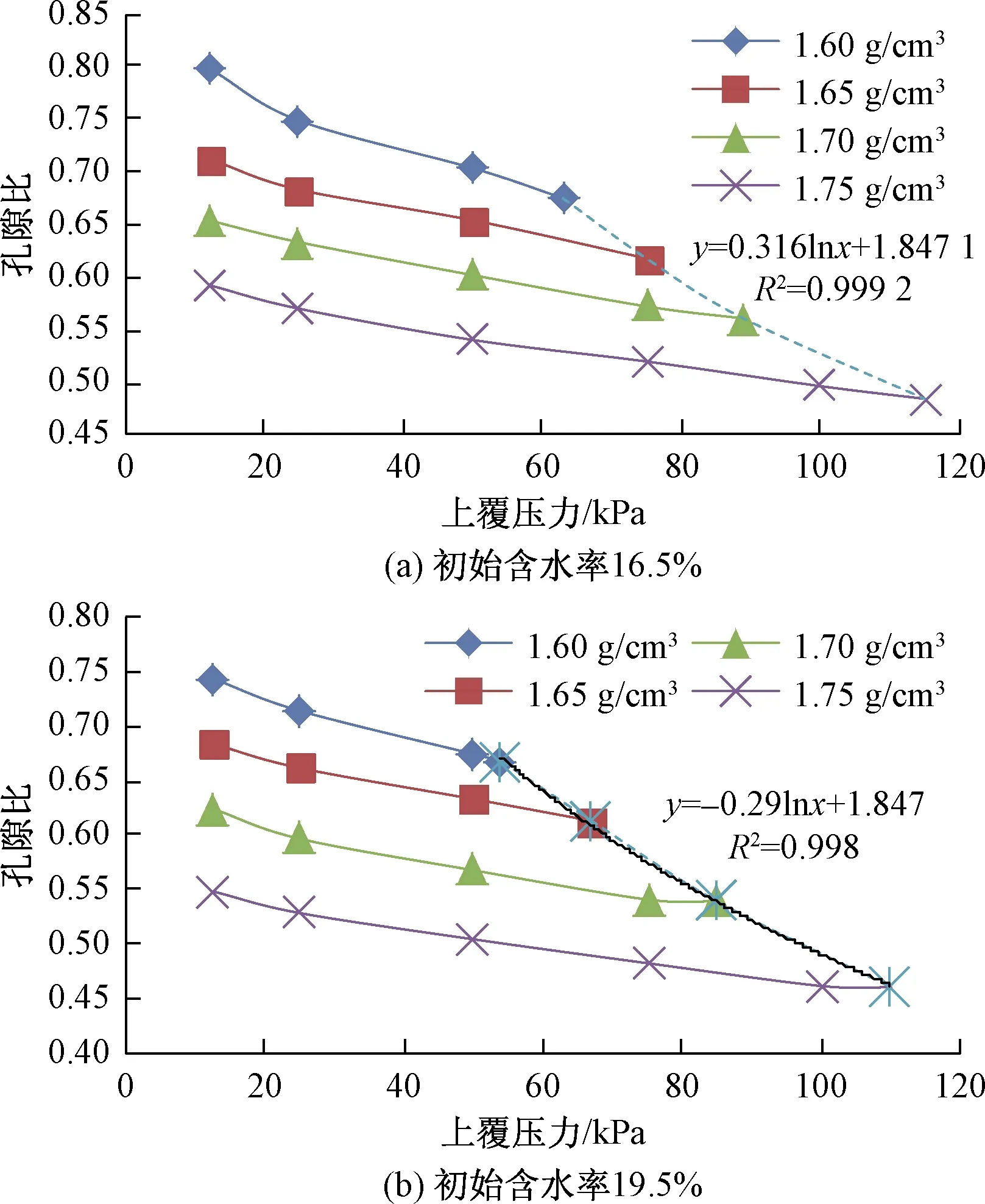
图6 膨胀区膨胀变形曲线Fig.6 Expansive deformation curve of the expansive region

由图6可见，2种初始含水率下土体的膨胀变形区曲线基本相似，表明初始含水率对于不同初始干密度土体膨胀变形特性的影响基本一致。图6中虚线为2种初始含水率在4种不同初始干密度下，浸水膨胀与压缩区分界点的上覆压力与孔隙比关系曲线。将浸水膨胀与压缩分界点的孔隙比与上覆压力关系采用对数的线性关系拟合：

ef=klnPf+b2

(4)

式中：ef——分界点孔隙比；

Pf——上覆压力；

k，b2——相关系数。

将图6中2种含水率浸水膨胀与压缩分界点曲线的斜率值与表1中2种初始含水率的土体上覆压力与孔隙比关系曲线斜率k值列于表2中。

将表2中各初始状态下的k值与分界点的k值进行比较，可以看出，在相同的含水率下，k值随着初始干密度的增大而逐渐增大，逐渐逼近与分界点的上覆压力与孔隙比关系曲线的k值。这表明在某一初始状态下，土体的上覆压力与孔隙比关系曲线与膨胀与压缩曲线分界点的上覆压力与孔隙比关系曲线可能重合，表明在某些初始状态下土体浸水后既不发生膨胀变形现象，也不发生压缩变形现象，这一推断在已有的研究结论中得到了论证[13]。

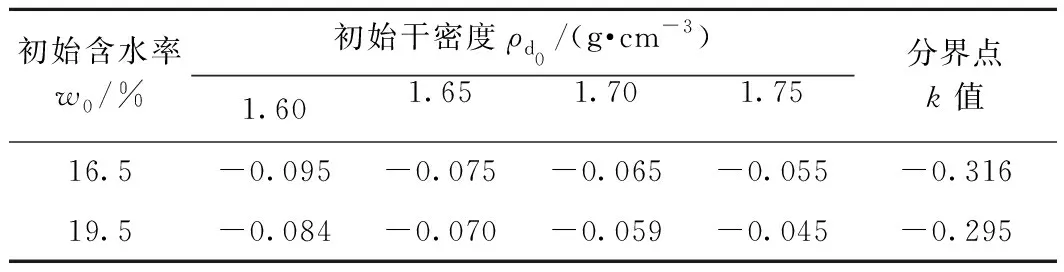
表2 各初始状态下k值及分界点k值

3 膨胀变形量的预测及应用

3.1 膨胀变形量的预测

将土体的含水量换算为饱和度，并与表1中k值进行拟合，将拟合结果绘于图7中。

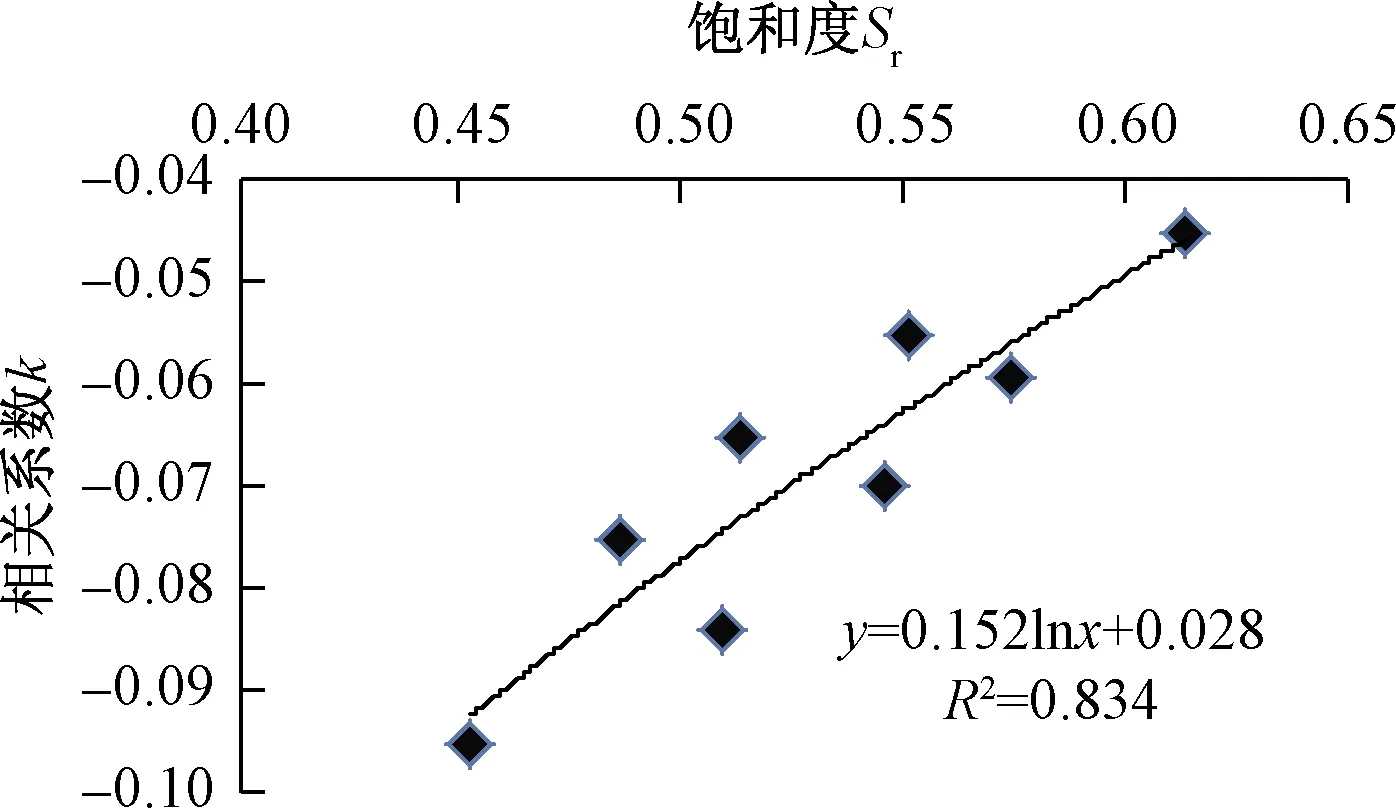
图7 初始饱和度与k值关系曲线Fig.7 Relationship between the initial dry density and k

由图7可见，在2种相同初始含水率下，土体的初始干密度与k值基本呈线性关系，可以表示为：

k=0.152lnSr+0.028 4

(5)

若已知初始干密度和初始含水率，可确定土体的初始饱和度，并由式(5)确定膨胀变形曲线k值。在相同初始含水率下，已知土体的初始干密度，由式(3)确定分界点的上覆压力，将求出的上覆压力值代入式(4)得出分界点的孔隙比ef。

由式(2)可知，膨胀过程土体孔隙比的变化可表示为：

Δep=ΔklnP

(6)

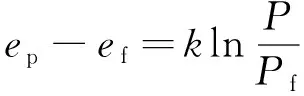
(7)

侧限条件下，浸水膨胀稳定后的孔隙比和固结稳定后的孔隙比满足：

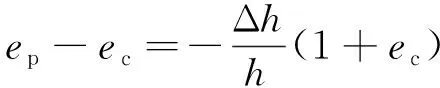
(8)

将式(8)式代入(7)式，可得：

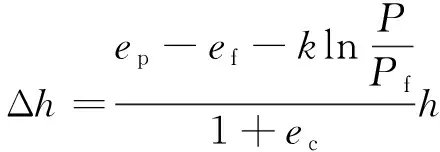
(9)

式中：Δh——浸水前后土体的膨胀变形量；

ec——固结稳定后的孔隙比；

ef——分界点的孔隙比。

3.2 膨胀变形量计算方法的应用

将土体用于路堤填筑中，文献[14]要求路堤各层的压实度要求如表3所示。

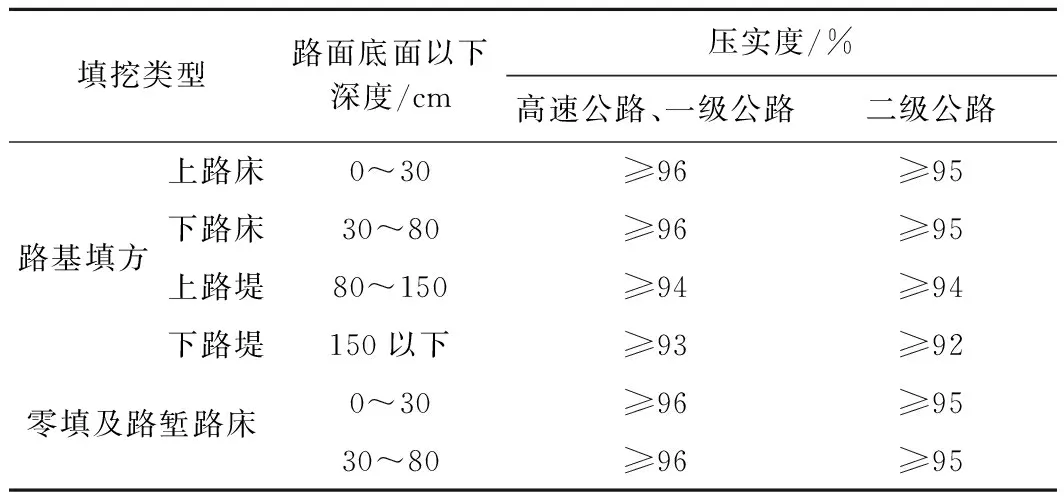
表3 路堤压实度标准[14]

弱膨胀土用于工程包边法路堤填筑对于包边宽度及厚度的确定，目前还没有统一的方法，余飞等[15]、杨和平等[16]、膨胀土地区建筑技术规范[17]均提出了包边厚度的确定方法。总体而言，膨胀土路堤的处置深度均大于1.5 m(图中的B值)，图8为工程包边法路堤的结构简图。

图8 工程包边法路堤结构图Fig.8 The subgrade structure figure of engineer wrapper methods

按照表4及图8中B厚度的要求，下路堤以上土体基本均经过石灰处理，因此，用于路堤填芯膨胀土的压实度一般为92%～93%，固结稳定后的孔隙比基本一致。采用分层总和法对土体进行膨胀变形量的计算：

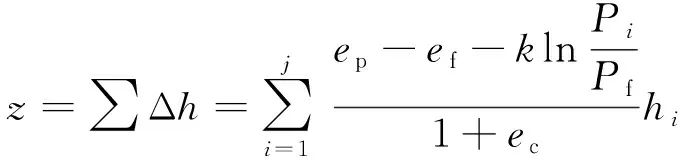
(10)

在路堤土体浸水饱和过程中，在较小的上覆压力下土体发生膨胀变形，在较大的上覆压力下发生压缩变形。图9为路堤土体浸水饱和区的上覆压力分布情况(假定路堤土体为均质土体，且不考虑用石灰改良土与素土的干密度差值)。用于包边石灰土厚度H0产生的上覆压力以附加应力的方式表示，即图9中上覆压力F。

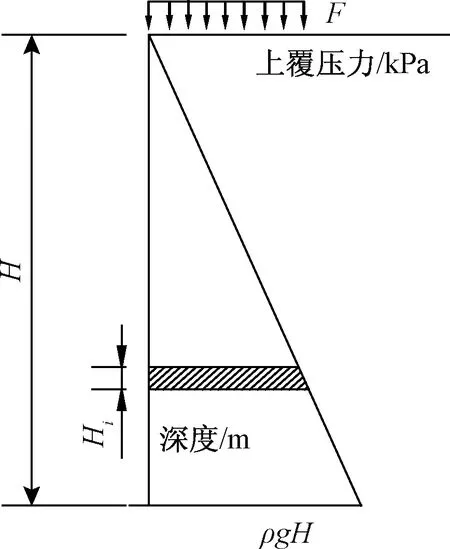
图9 不同深度的上覆压力分布Fig.9 Overlying press distribution in different depthH—土体分界点竖向压力深度；F—用于包边石灰改良膨胀土所产生的上覆压力；Hi—土体分层厚度。

将分界点上覆压力深度以上范围内的土层划分为j层，则每层土体的厚度Hi可以采用式Hi=H/j表示。则第i层土体的上覆压力Pi=F+ρg[(2i-1)/2j]H。

将第i层土体的上覆压力Pi及分界点上覆压力Pf=ρgH代入式(10)，可得：

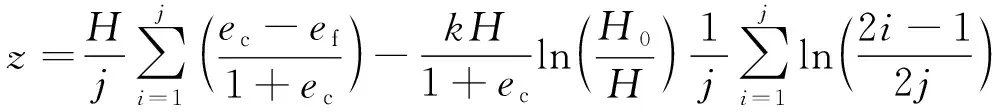
(11)

式中：H0——石灰土包边的厚度。

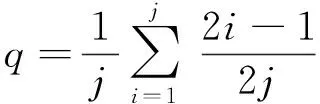
(12)

将(12)式化简得：

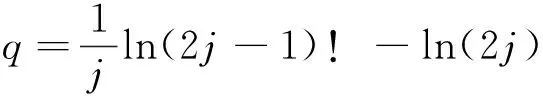
(13)

分别令j=1，2，3，4，…，将不同j值下的q值绘于图10中。

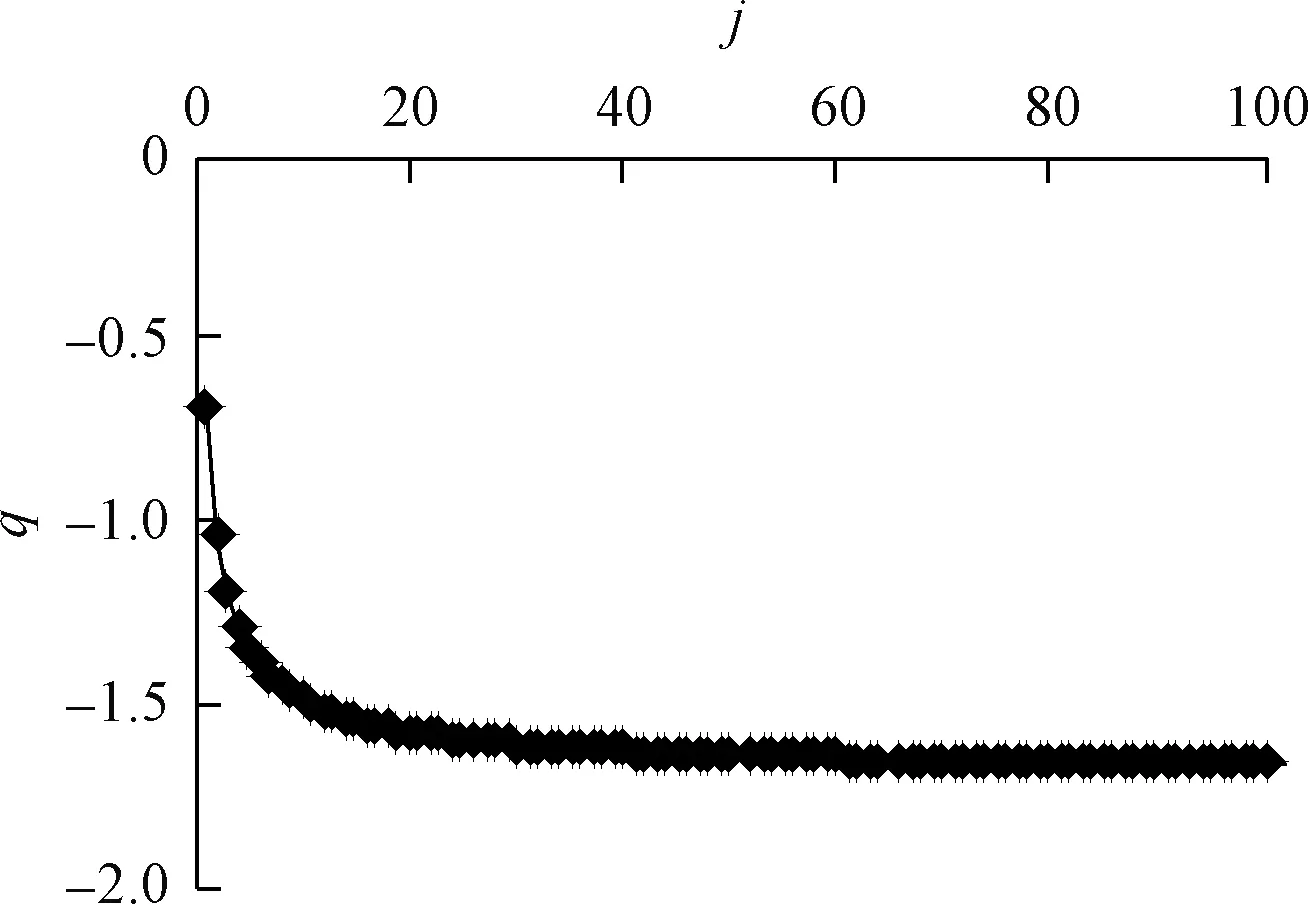
图10 j与q值的关系Fig.10 Relationship between j and q

可见，随着j值的增加，q逐渐减小，取前后2次q差值小于1%的j值作为q的稳定值，故取j=10作为分层数，计算得到q=-1.485 3，并将j=10，q=-1.485 3代入(11)式，可得：

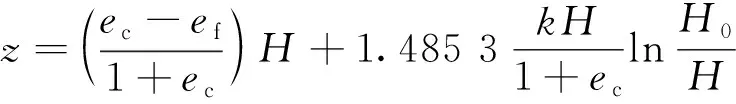
(14)

4 结论

(1)在不同的初始含水率及初始干密度下，膨胀土的固结及膨胀曲线呈现相似的规律。土体浸水饱和状态线的孔隙比随着上覆压力的增大而逐渐减小。随着上覆压力的增大，不同初始含水率及初始干密度下土体浸水饱和后的孔隙比趋于一致十分明显。

(2)在初始含水率及初始干密度下，膨胀土的固结与膨胀曲线均存在分界点，且分界点的上覆压力与初始干密度及分界点的孔隙比均呈线性关系。且在相同的初始干密度下，含水率越大的土体，分界点的上覆压力越小。

(3)基于膨胀土固结与浸水膨胀变形曲线分界点的特征，提出了弱膨胀土膨胀变形量的计算公式，并利用计算公式对简化条件下路堤的变形量进行了预测。