基于桩体抗剪强度的复合地基路堤稳定性分析方法

2020-09-27钟昌茂邱恩喜魏永幸王智猛刘菀茹万旭升李康乐

水文地质工程地质 2020年5期

钟昌茂，邱恩喜，魏永幸，王智猛，刘菀茹，万旭升，李康乐

(1.西南石油大学土木工程与测绘学院，四川成都 610500; 2.中铁二院工程集团有限责任公司，四川成都 610031)

路堤修建过程中，常遇到承载力较低的软弱地基，导致路堤出现滑塌失稳、变形沉降等工程病害，严重威胁铁路工程的顺利修建和稳定运营。而水泥土搅拌桩复合地基是工程中处理软基的常用方法，因此对水泥搅拌桩等加固的复合地基路堤边坡稳定性分析及处置技术进行深入研究具有重要意义。边坡稳定性分析理论主要有刚体极限平衡理论、变形分析理论和塑性极限分析理论三种[1]，刚体极限平衡理论常采用瑞典圆弧法、Bishop法、Janbu法等。土质边坡失稳时临界滑动面常呈现为圆弧状或呈折线状[2]，在《铁路路基设计规范》(TB 10001—2016)中针对路基失稳时的边界形状提供了圆弧滑动法、平面滑动和折线滑动三种边坡稳定性计算方法。变形分析理论是将土坡稳定与变形结合起来，利用有限元等数值计算对边坡的稳定性进行计算[3-5]。塑性极限分析理论则是基于极限状态条件下的能量守恒原理(即外力功率与内部能量消耗平衡)，以求解边坡稳定稳定系数[6-7]。本文基于刚体极限平衡理论中的瑞典圆弧法与毕肖普法，对水泥土搅拌桩加固地基的路堤边坡稳定性进行分析。

对桩加固的复合地基路堤稳定性分析，根据《铁路路基设计规范》(TB 10001—2016)提供的方法，可将加固桩与桩间土两部分的强度参数整体复合为单一的强度参数(以下简称规范法)，进而计算路基和路堤整体稳定性。但是在复合为单一强度参数后，其桩体强度参数有所折减，所求出的稳定系数并非为真实稳定系数，其折减值与复合地基的置换率、路基高度、桩体参数等有一定关系。并且，有研究表明，采用折减的强度参数计算边坡稳定性时会导致计算结果的失真[8-9]。

本文基于规范所提供设计方法，提出了新构思，即分别计算出加固桩和桩间土抗剪强度，并进一步计算出加固桩和桩间土的稳定力矩和滑动力矩，最后得到路堤边坡稳定系数。研究表明，基于桩-土分算方法的稳定系数大于规范法计算所得稳定系数，两种方法计算的稳定系数差值呈现出一定规律性。并且，对于已加固边坡，规范法分析所得最不利圆弧滑面穿过柔性桩加固区，但桩-土分算法分析所得最不利滑面位于加固桩底部以下区域，绕过了柔性桩加固区，更加接近实际情况。

1 复合地基稳定性计算规范法

根据《铁路路基设计规范》(TB 10001—2016)，计算圆弧滑动型路基及路堤整体稳定性时可采用瑞典条分法，但不通过单桩抗剪强度计算滑动力矩，而是采用加固桩与桩间土两部分强度参数整体复合为单一强度参数，进而计算路基及路堤整体稳定性。

1.1 散体材料桩复合地基抗剪强度指标

散体材料桩加固的复合地基，其抗剪强度指标按式(1)、式(2)进行确定：

cc=(1-m)cs

(1)

tgφc=(1-m)tgφs+mtgφp

(2)

式中：cc，φc——复合地基土的黏聚力和内摩擦角；

cs，φs——桩间土的黏聚力和内摩擦角；

φp——桩体内摩擦角；

m——复合地基置换率，根据桩承担面积的不同，采用公式m=nAp/A进行计算[10](Ap为单桩面积，A为桩周复合土体单元面积，n为桩的根数)。

1.2 柔性桩复合地基抗剪强度指标

柔性桩复合地基抗剪强度按式(3)进行确定：

τc=mτp+(1-m)τs

(3)

式中：τc——复合地基的抗剪强度；

τp——桩体的抗剪强度；

τs——桩间土的抗剪强度。

1.3 稳定系数计算

根据式(1)、式(2)或式(3)获得复合地基抗剪强度参数后，其稳定系数K可按式(4)计算，计算示意图如图1所示。

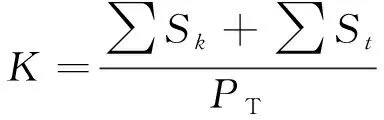
(4)

PT=∑Wksinαk+∑Wtsinαt

Sk=Wkcosαktgφqk+cqklk

St=Wtcosαttgφqt+cqtlt

Wk=Wck+Wdk

式中：PT——各土条在滑弧切线方向的下滑力和；

Sk——地基土内(AC弧)抗剪力；

St——路堤内(CD弧)抗剪力；

Wk，Wt——第k条、第t条土条重量。下标k，t表示土条编号，k表示土条底部滑裂面在地基土层内，t表示土条底部的滑裂面在路堤填料内；

Wdk，Wck——当第k土条滑裂面处于地基内(AC弧)时，分别为滑面以上该土条中的地基自重及路堤自重；

αk，αt——第k、第t土条底滑面的倾角；

lk，lt——第k、第t土条底滑面的长度；

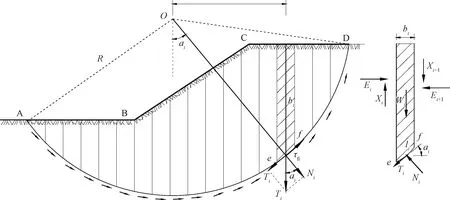
图2 瑞典条分法计算路堤边坡稳定性示意图Fig.2 Schematic diagram of the Swedish arc method for calculating embankment stability

R——滑动圆弧半径；

cqk，φqk——当第k土条滑裂面处于地基内(AC弧)时，分别为该土条所在土层的快剪黏聚力及快剪内摩擦角；

cqt，φqt——当第t土条滑裂面处于路堤内(CD弧)时，分别为该土条所在路堤填料的黏聚力与内摩擦角。

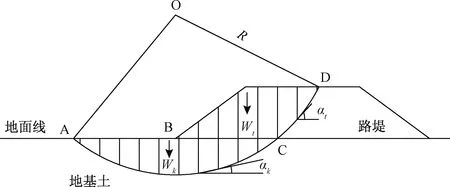
图1 规范法计算路堤稳定性示意图Fig.1 Schematic diagram for calculating the stability of embankment by the criterion method

2 复合地基稳定性桩-土分算计算原理

2.1 桩-土分算瑞典条分法

基于边坡圆弧滑动破坏方式，分别计算加固桩和桩间土的抗剪强度，最后得出路基边坡稳定系数K。如图2所示土坡，未加固时，取单位长度土坡按平面问题计算。设可能滑动面为圆弧AD，圆心为O，半径为R。

将滑动土体ABCD分成许多竖向土条，任一土条i上的作用力包括土条重力Wi、滑动面ef上的法向力Ni及切向反力Ti、土条两侧的法向力Ei，Ei+1及竖向剪切力Xi，Xi+1。(假定土条和桩两侧Ei和Xi的合力等于Ei+1和Xi+1的合力，同时它们的作用线也重合，因此土条和桩两侧的作用力相互抵消[11])：

Ni=Wicosαi

(5)

Ti=Wisinαi

(6)

滑动面ef上的抗剪强度τfi：

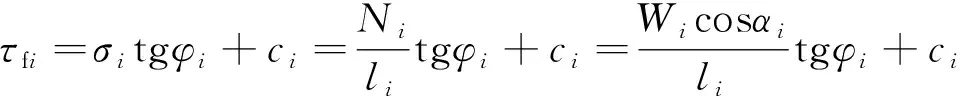
(7)

式中：αi——土条i滑动面的法线(亦即半径)与竖直线的夹角；

σi——滑面ef所受正应力；

ci，φi——滑动面上地基土或路堤填料的黏聚力及内摩擦角。

土条i上的作用力对圆心O产生的滑动力矩Ms及稳定力矩Mr分别为：

Ms=TiR=WiRsinαi

(8)

Mr=τfiliR=(Wicosαitgφi+cili)R

(9)

加固桩存在时，如图3所示土坡，取长度为lz的(lz为复合地基加固桩的桩间距)土坡按平面问题计算。同样设可能滑动面为圆弧AD，圆心为O，半径为R，并将滑动土体 ACDBA分成许多竖向土条，对土条进行受力分析。假定滑面内有b根桩，桩滑面gh的面积s为：

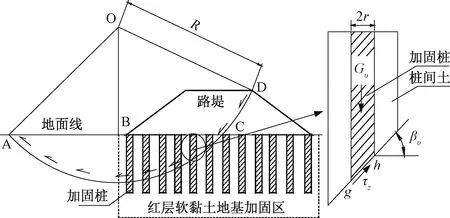
图3 复合地基路堤稳定性桩-土分算示意图Fig.3 Stability diagram of embankment with composite foundation

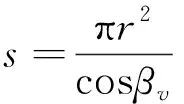
(10)

式中：βv——桩v滑动面的法线(亦即半径)与竖直线的夹角；

r——桩的半径。

则桩v上的抗剪力对圆心O产生的稳定力矩Mz为：

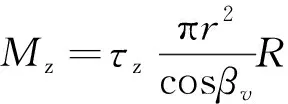
(11)

(12)

式中：τz——加固桩v的抗剪强度；

Gv——加固桩滑面gh所受竖向压力；

cv，φv——加固桩v的黏聚力及内摩擦角。

桩所置换的土条u产生的稳定力矩Mc：

(13)

式中：Gu——桩置换土作用在滑面gh的竖向压力。

则整个土坡相应于滑动面为ACD时的稳定系数K：

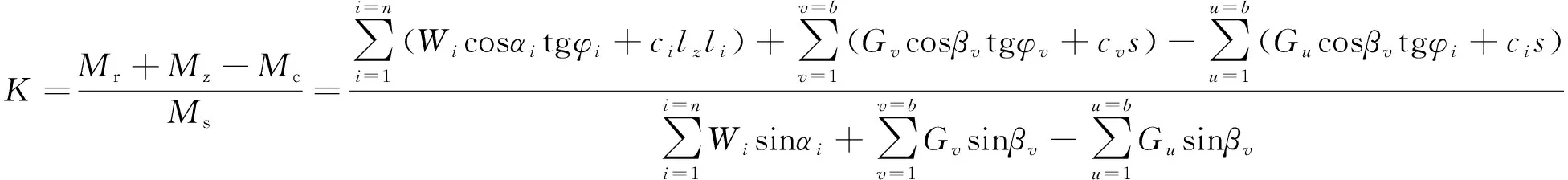
(14)

式中：Ms——复合地基路堤对圆心O产生的滑动力矩。

2.2 桩-土分算毕肖普法

对于复合地基路堤稳定性，在考虑桩体抗剪强度情况下还可采用简化毕肖普法进行分析[11]：

如图2所示土坡，由土条i的竖向平衡条件有：

Nicosαi=Wi+Xi+1-Xi-Tisinαi

(15)

假定τfi与滑面上的切向力Ti相平衡，则：

(16)

将式(16)代入式(15)得：

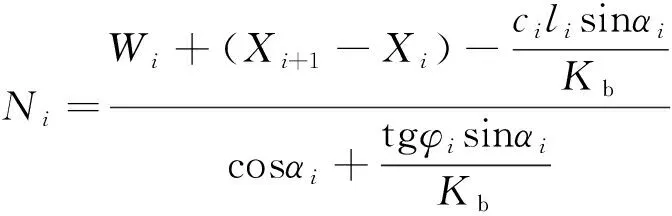
(17)

已知土坡的稳定力矩为：

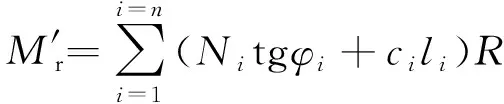
(18)

将式(17)代入式(18)有：

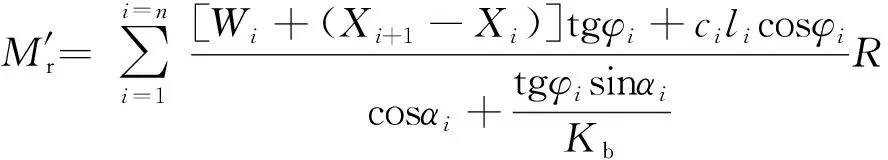
(19)

毕肖普假定土条间竖向剪切力Xi=Xi+1，得：

(20)

同理，边坡中加固桩的稳定力Mz矩为：

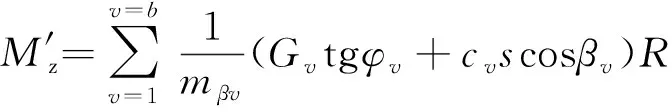
(21)

加固桩置换土条的稳定力M′c矩为：

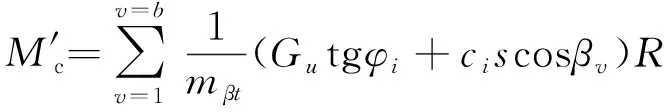
(22)

则路堤边坡稳定系数Kb为：

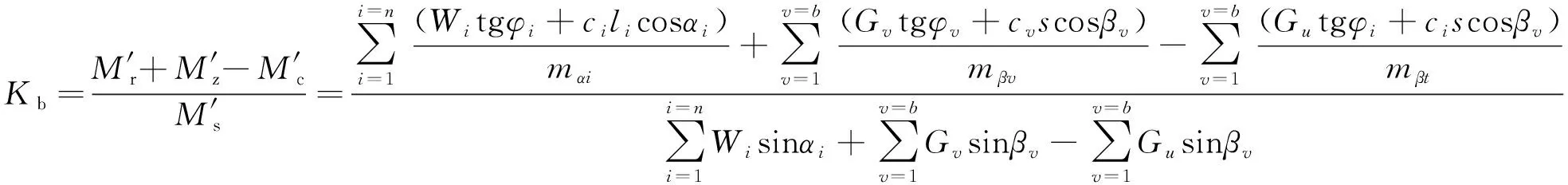
(23)

式中：M′s——复合地基路堤对圆心O产生的滑动力矩。

3 边坡稳定系数及破坏特点研究

3.1 计算案例

以路堤边坡填高分别为3，6，9，12和15 m为例，对路堤边坡稳定系数K进行计算，路堤上部填料重度为20 kN/m3，φ=36°，c=54 kPa；下部红黏土软基参数为φ=5°，c=10 kPa，重度为19 kN/m3。采用水泥搅拌桩加固路堤，强度参数如表1所示，桩直径分别为0.5 m和0.8 m，间距分别设置为1.2，1.5和1.8 m，正方形布置。软基加固深度分别为10，15，20，25和30 m，均穿过未加固时的边坡最不利滑动破坏面。

3.2 地基边坡稳定系数变化规律

在路基高度为3，6，9，12和15 m、搅拌桩水泥掺入量为20%、并养护90 d的情况下，对各边坡未加固时的最不利滑面的稳定性进行分析。结果如图4所示，在桩径及桩距相同的情况下，桩-土分算瑞典条分法的(式(14))、规范法(式(4))以及桩-土分算毕肖普法(式(23))计算所得稳定系数均随路堤高度增加而降低。

表1 水泥土搅拌桩强度参数[12]

图4 桩-土分算法与规范法分析所得路堤边坡稳定系数Fig.4 Safety factor of embankment slope calculated based on new methods and specification method

规范法计算所得路堤边坡稳定系数见图4(a)，稳定系数最大值和最小值出现在边坡高度为3 m和15 m时，分别介于2.94～14.51和0.98～3.41之间。基于桩-土分算瑞典条分法的路堤稳定系数见图4(b)。其最大值出现在边坡高度为3 m时，范围为4.21～16.51；最小值则为边坡高度15 m时，范围为1.37～3.93。

图4(c)为桩-土分算毕肖普法的稳定系数计算值。当路基高度为3 m时其稳定系数最大，范围为4.01～13.86；当边坡高度为15 m时，其稳定系数最小，范围为1.37～3.60。图4(a)—(c)间的对比表明，在桩径、桩距及边坡高度相同的情况下，桩-土分算毕肖普法所得稳定系数低于桩-土分算瑞典条分法法稳定系数，但高于规范法计算所得稳定系数。

图5为规范法计算所得路堤稳定系数与桩-土分算瑞典条分法所得稳定系数差值率μ，其值随边坡高度呈抛物线形变化：

(24)

式中：K分算法——公式(14)计算所得稳定系数；

K规范法——公式(4)计算所得稳定系数。

在桩距为1.2 m时，稳定系数差值率随路堤高度从3 m增加到9 m时呈上升趋势，最大值在桩径为0.8 m及路堤坡高为9 m时达到，为19.6%；当路堤坡高从9 m增加到15 m时，差值率则呈下降趋势，但最小值出现在边坡高度3 m时(图5a、c)。差值率随路堤的高度不断增大而先增大后减小，总体趋势呈抛物线形变化。

在桩距为1.8 m的情况下，稳定系数差值率随路堤高度仍然呈先增大后减小的抛物线形变化，但其峰值提前出现在路堤高度为6 m的情况下。即差值率最大值出现在桩径为0.8 m及路堤坡高为6 m时，为40.3%。

图6为桩-土分算瑞典条分法与桩-土分算毕肖普法求得的稳定系数差值率。结果表明，采用后者计算出来的稳定系数总体低于桩-土分算瑞典条分法的稳定系数。两者差值率随路堤高度增加及桩距的增大减小，随桩径的增大而增大，近似线性变化。总体而言，2种桩-土分算法得到的稳定系数差值率位于0～18%范围内。

由于规范法是将桩体的强度参数与土体的强度参数进行复合为一整体计算，这一方法虽然在理论上确实提高了土体的强度参数，但是也折减了桩体的强度参数，故小于实际的稳定系数值。

因此，桩-土分算法更加接近工程实际，而规范法则更偏保守。路堤边坡稳定系数计算结果表明，基于3种方法的稳定系数在边坡高度较高时均较为接近，此时差值也较小。

3.3 路堤边坡破坏特点分析

上述研究表明，采用桩-土分算法和规范法对同一路堤稳定性进行分析将获得不同稳定系数，同时，基于不同方法的路堤最不利滑面及其剪入剪出口也具有差异性。图7为不同方法分析的路堤最不利滑面位置，其中，加固桩为7%水泥含量的水泥土搅拌桩，养护龄期为90 d，桩径为0.5 m，桩间距1.5 m。

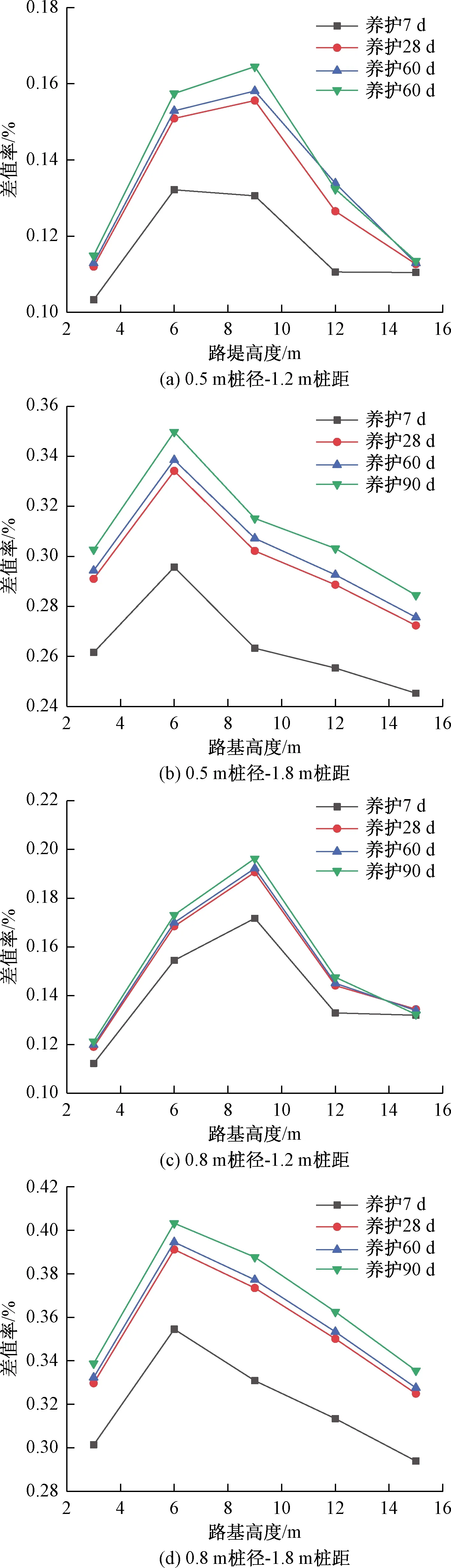
图5 桩-土分算瑞典条分法与规范法的路堤稳定系数差值率随路堤高度、加固桩径和桩距变化规律Fig.5 Law of difference in the safety factor of the new Swedish arc method and the standard method varies with the height of the roadbed, the pile diameter and the pile distance

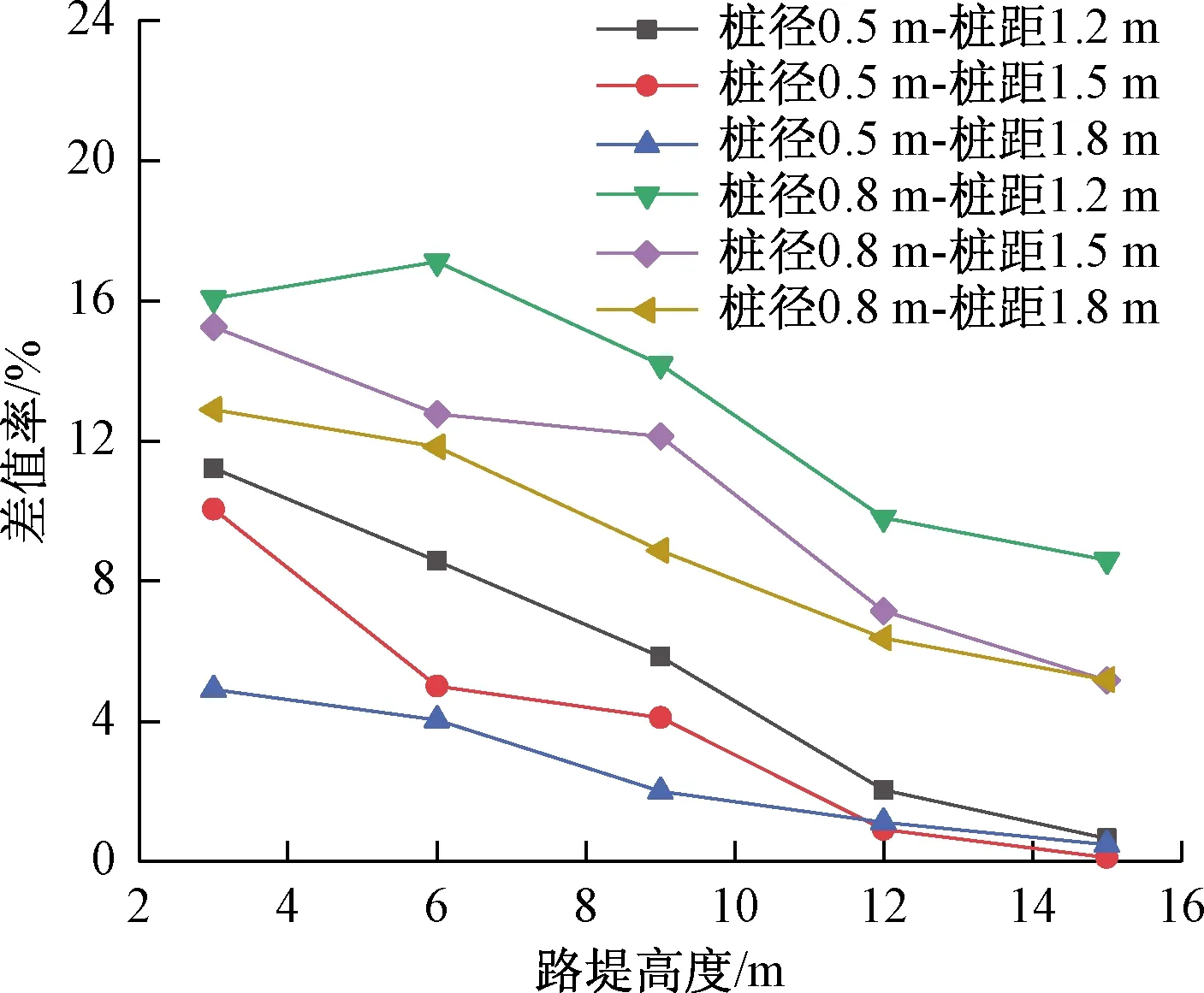
图6 桩-土分算瑞典条分法与桩-土分算毕肖普法所求稳定系数差值率Fig.6 Safety factor difference rate of the Bishop’s method and the Swedish arc method

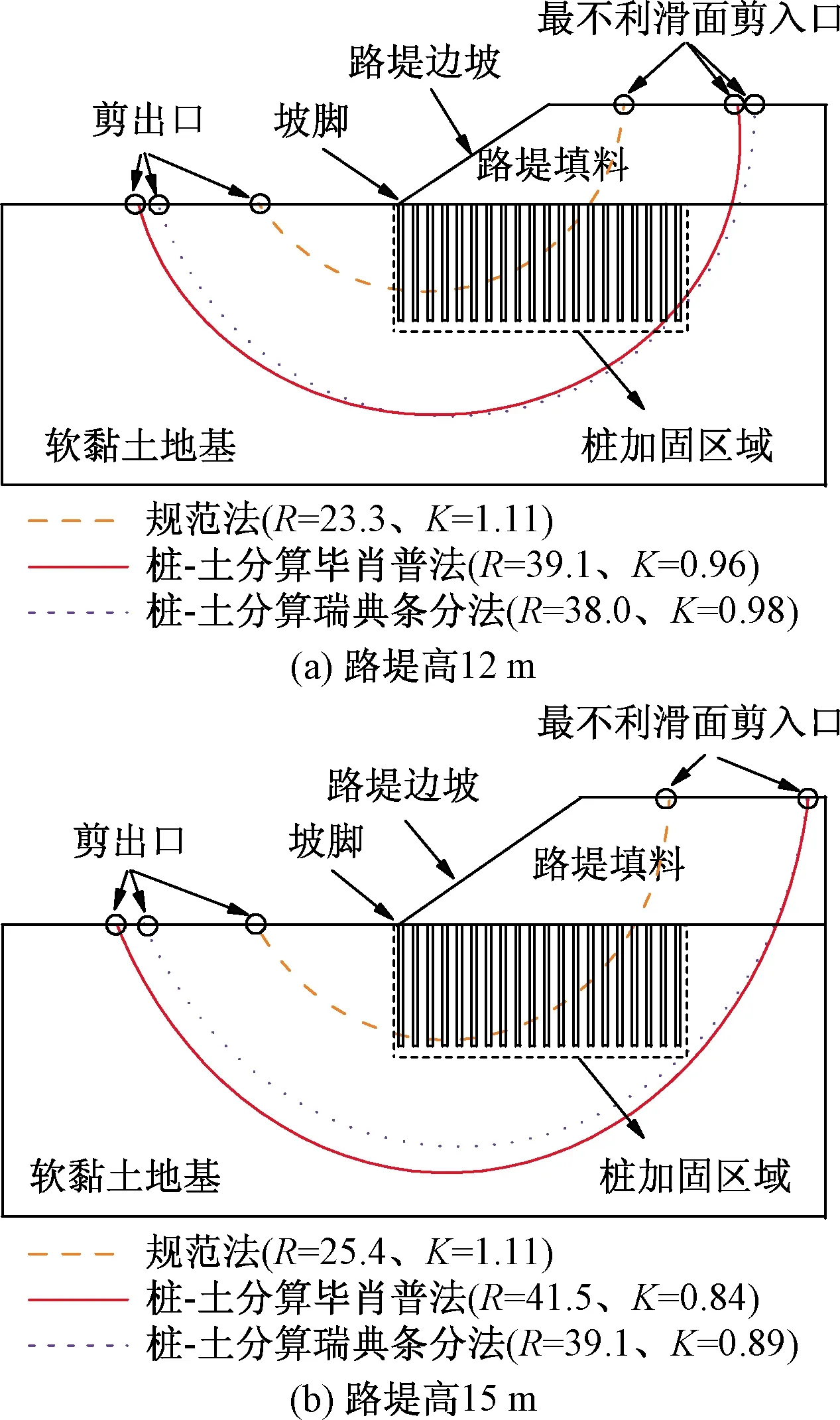
图7 三种方法下的路堤最不利滑面随路堤高度变化规律Fig.7 Variation in the most unfavorable slip surface of the embankment under different methods with the height of the embankment

当路堤高度为12 m时(图7a)，基于规范法求得的路堤最不利滑面穿过路堤加固区域中部，滑面半径及稳定系数与9 m高路堤相同，剪入剪出口位置没有较大变化；而基于桩-土分算的毕肖普和瑞典条分法分析得最不利滑面均出现在加固桩最右侧桩底部，剪入口在最右侧加固桩的右边，剪出口位于路堤坡脚较远处。当路堤高度继续增加到15 m时(图7b)，3种方法分析的最不利滑面位置与路堤高度为12 m时相同，但滑面半径增大1～3 m。因此，最不利滑面剪入口均向路堤右侧移动，而路堤剪出口向远离路堤坡脚方向移动。

采用桩-土分算法对本文其他案例进行分析表明，最不利滑面位置主要受路堤高度影响。桩-土分算瑞典条分法分析结果表明，当路堤高度为9～15 m时，最不利滑面将出现在桩加固区底部，而路堤高度较低的情况下则不会出现这种情况。而桩-土分算毕肖普法分析结果表明，最不利滑面出现在桩加固区底部的情况同样是在路堤高度较高(12 m和15 m)的情况下，即最不利滑面位置出现了“下移”现象，并且加固后的边坡整体仍然存在不稳定性。

从计算原理分析，由于规范法是将加固桩与桩间土复合成一个整体，进而分析地基整体稳定性，所以路堤边坡最不利滑面始终在路堤中部。而桩-土分算法考虑了加固桩桩体的抗剪强度，所以在桩加固区域，路堤边坡稳定性较好，不会出现最不利滑面。如图7所示，随路堤高度增加，桩-土分算法分析所得最不利滑面始终位于加固桩桩体底端以下区域。