考虑均衡性的城际铁路列车运行图智能调整方法研究
2020-09-27郭一唯黄艨靼
郭一唯,黄艨靼,李 博,何 清
(1.中国铁道科学研究院集团有限公司 运输及经济研究所,北京 100081;2.中国科学院 智能信息处理重点实验室,北京 100190;3.中国科学院 计算技术研究所,北京 100190;4.中国科学院大学 计算机科学与技术学院,北京 100049)
列车运行图是铁路行车组织的基础,是对铁路运输各部门工作的统筹计划。列车运行图的编制与调整是一项复杂而艰巨的工作,常常需要消耗大量的时间和人力成本。随着信息技术的高速发展,国内外相关领域的专家学者以实现列车运行图编制与调整的自动化、智能化为目标,开展了许多理论方法层面的有益探索和尝试。人工智能方法在围棋领域的成功应用[1]引起关注,既有研究对高速铁路调度指挥场景下利用人工智能方法解决列车运行实时调整问题展开初步探索[2-4],但对于列车运行计划编制阶段的运行图调整问题还鲜有涉及;针对列车运行图的调整与优化问题,往往以运筹学模型方法为基础框架,当遇到难以高效求解的场景时,需要借助专家知识和既有经验,提出各种调整策略或启发式算法以实现运行图的优化[5-6]。但是,这些方法在求解大规模列车运行图问题时仍然存在一定的困难。因此,亟需借鉴人工智能方法在其他领域应用的成功经验,利用人工智能方法初步探索和解决计划编制阶段的列车运行图调整问题,为解决该问题提供一种可行的方法。
1 考虑均衡性的城际铁路列车运行图调整模型构建
1.1 影响因素
城际铁路列车运行图的调整涉及铁路运输组织和管理中的众多环节,其影响因素如下。①客流需求因素。列车起讫点,列车始发、终到时间,列车中途停站地点和时间,相同起讫点、相同停站结构的列车在运行图上的分布,相同起讫点、不同停站结构的列车在运行图上的分布等。②动车组运用因素。动车组周转计划、动车组分配计划、动车组检修计划。③车站作业因素。到发线运用计划,吸污、上水作业计划等。④行车安全因素。列车区间运行时分、列车起停车附加时分、列车区间追踪间隔时间、车站追踪间隔时间等。⑤能力利用因素。繁忙线路区段内的点线能力协调、繁忙线路区段之间的能力协调运用等。⑥其他影响因素。独门车、标杆车等特殊列车的编图要求。
1.2 模型构建
1.2.1 模型假设
(1)线路的封闭性假设。假设所考虑的线路区段是相对封闭的,没有跨线列车的干扰,可以对该区段运行图进行一体化编制和调整。
(2)运行图参数已知假设。假设列车区间运行时分、列车起停车附加时分、列车区间追踪间隔时间、车站追踪间隔时间、各主要车站的停站频次以及每次停站的时间范围标准等约束条件是给定的。
(3)不考虑其他计划假设。假设动车组交路计划、车站到发线分配计划都是相对灵活的,在列车运行图的编制和调整过程中暂不考虑。
(4)列车无越行假设。假设同方向列车之间不发生越行。
1.2.2 模型描述
城际铁路列车运行图的调整问题可以表示为离散时间马尔可夫决策过程,其具体的特征如下。
(1)环境状态集合S。给定待研究的线路区段(包含车站、区间等设施信息),可以将在一定时间范围内所有列车的每种可能的时空分布(运行图不一定可行)定义为一个环境状态st,其中t为一个离散时间步序列(t= 0,1,…),并将所有可能的列车时空分布状态的集合定义为模型的环境状态集合S= {st}。在不考虑车站到发线分配方案的情况下,每个环境状态st仅包含运行图上各列车的起讫点、运行径路、在径路上各站的到达和出发时刻信息,而不包含列车在沿途各站的到发线分配信息。
(2)动作集合A。动作集合可以分为3个动作大类:平移(A1)、交换(A2)和改变停站时间(A3)。每个动作大类又由数量不等的基本动作(如向右平移1 min、向左平移300 min、交换编号为2和编号为245的2条运行线)组成。
(3)策略集合π。在时间步t,面对一个需要调优的环境状态st,对每个可选动作at的选择概率πq=P(at|st)称作一个策略,则策略集合为π= {πq}(q= 0,1,2,…,N)。策略集合是一个有限集合,需要通过对相关数据的采样和训练得到。
(4)环境的奖励R。在时间步t,智能体选择并实施了动作at后,环境对该动作的反馈信号值称作奖励,记为R。而R=R(st,at,st+1)是当前环境状态、当前所选动作以及下一时间步环境状态的标量函数。奖励主要用于计算收获,而R本身是由运行图图面打分函数计算得到。
(5)收获G。收获是奖励R随时间步的累积值, 对 于 时 间 步t, 收 获Gt=Rt+1+γRt+2+γ2Rt+3+… =Rt+1+γGt+1,其中γ∈ [0,1]称为折扣因子,其主要反映距离当前时间步越近的奖励越重要。收获G用于对策略集合进行训练和估计。
1.3 模型求解
为了求解城际铁路列车运行图调整问题的离散时间马尔可夫决策过程模型,提出以下2个关键算法。
1.3.1 运行图图面打分函数
运行图的可行性和运行图列车分布的均衡性是衡量运行图一体化调整优化质量的重要评价标准。为此,设计运行图图面打分函数,计算模型中的环境奖励R,进而对策略集合进行训练和估计。运行图图面打分函数为

式中:Score(st)是对图面(对应于在某个时间步的环境状态st)进行总体打分的函数;μ和ω为常量参数,需要结合具体案例通过多次实验估计得到;ev(st)是图面均衡性打分函数,由公式 ⑵ 至 ⑸ 式给出;conf(st)是图面冲突严重程度打分函数,由公式⑹给出。

式中:σi(st)是在时间步t的图面上服务于第i对旅客OD之间的相邻列车出发间隔时间的标准差,每对可能的旅客OD之间运行的所有列车都参与计算,包括在起站(O)始发在讫站(D)终到、在起站始发在讫站停留后通过、在起站停留后通过在讫站终到、在起讫站均停留后通过4种列车。Yi= (yi,1,yi,2,…,yi,ni-1)表示服务于第i对旅客OD之间的相邻列车出发间隔时间向量,是由服务于第i对旅客OD之间的列车出发时刻顺序排列向量Xi= (xi,1,xi,2,…,xi,ni)通过公式 ⑷ 求得。E(Yi)是Yi的数学期望。关于运行图均衡性量化分析的理论推导,可参考孙焰等[7]的相关论述。
运行图的可行性是均衡性的前提,因而需要对运行图图面的可行性进行打分评价。由于模型假设不考虑微观层面的车站到发线分配以及动车组交路计划,并且假设同方向列车之间不发生越行,因而可以将运行图可行性的评价转化为一个较为简单的图面冲突严重程度打分函数

式中:Ni,j,SX和Ni,j,XX分别为在环境状态st对应的图面上在车站i同时竞争时刻点j的上、下行列车数量;m为在所考虑的线路区段内的车站数;n为需要进行冲突检查的时刻的总数,如果时间粒度为1 min,则在环境状态st对应的图面上,n<1 440。
将conf(st)设计为一个二次函数,主要体现冲突检查与化解任务的重要性,让经过训练的“智能体”在运行图调整的过程中优先处理冲突检查与化解,而后考虑寻求均衡性的目标。
基于公式 ⑴ 至 ⑹ 定义的运行图图面打分函数,在时间步t实施某个动作at的环境奖励值R的计算公式为

1.3.2 Sarsa算法
Sarsa算法是一种在策略(on-policy)强化学习算法[8],其主要思路是通过定义Q函数(动作值函数),把在线产生的状态、动作和奖励的采样数据代入Q函数的更新公式里,通过迭代学习更新动作价值直至收敛。由Sarsa算法求得的动作价值可以看作是对相应收获G的一个有偏估计,因为它的采样序列并不是完整的状态序列。Sarsa的更新公式为

式中:α为学习因子;γ为折扣因子。
α和γ2个参数都需要结合具体案例通过多次实验估计得到。
2 案例验证
2.1 案例分析
选取京津城际铁路2018年年底的实绩运行图作为案例。京津城际铁路包含4种列车运行径路,分别为北京南城际场至天津城际场、北京南城际场至天津西城际场、北京南城际场至滨海(于家堡)和天津城际场至滨海。京津城际铁路线路示意图如图1所示。
通过分析实绩运行图可知,京津城际铁路列车具有以下3个特点:①除了在北京南城际场至天津城际场区段有4对/d去往东北方向的跨线列车外,剩余的129.5对/d列车均为本线列车,跨线列车比例很小,基本可以做到对所有本线列车在全天有效时间范围之内的统筹调整与优化;②本线列车的类型单一(均由设计时速350 km/h的8辆编组复兴号高速动车组担当),列车之间无越行情形发生,符合模型方法的前提假设;③除了亦庄、永乐2个车站暂无停站要求外,沿线其余各站均有服务频率和均衡性方面的需求,同时由于线路在南仓线路所分叉为2个方向,需要平衡兼顾不同运行区段之间的服务需求,与运行图图面统筹调整优化的思路吻合。
2.2 参数设置
在算例中,暂不考虑动车组交路和车站到发线分配方案的求解与生成,同时不考虑实绩运行图中北京南城际场至天津城际场区段内的4对/d跨线列车,仅考虑129.5对/d本线列车。算例相关参数配置如表1所示。
2.3 计算结果
本次算例实验运行在Windows 10系统环境下,运用Python结合C++语言编写程序代码,在Visual Studio 2017环境下编译,CPU为Intel酷睿i7-8750H (6核 )。

图1 京津城际铁路线路示意图Fig.1 Map of Beijing-Tianjin intercity railway

表1 算例相关参数配置Tab.1 Parameter configuration of the case study
为了对模型的策略集合π进行训练和估计,基于表1中的参数配置,通过对大量随机生成的有冲突且列车运行线排布不均匀的运行图图面的自动调整、推演、试错和学习,经过28 h的运算,得到了一个3 GB大小的策略查询字典文件,对应于在各种不同图面状态下为了朝最有利于冲突疏解和提高图面均衡性的方向发展,应当在下一个时间步选择实施的最佳或近似最佳动作。同时,经过训练后,得到公式 ⑴ 中的2个参数在μ= -1,ω= -15时有比较好的收敛效果。其中,参数取值为负,表示打分函数Score(st)的绝对值越低时,其对应的图面状态距离打分函数所寻求的最佳状态越接近。
得到策略集合之后,为了测试其在最不利情形下的效率和效果,基于表1中的参数配置,初始图面状态如图2所示。图2呈现出一个极端场景,即在各运行区段开行的不同起讫站、不同行别、不同停站结构的列车259列/d,在其各自的始发站的出发时刻都被“挤压”在早上6 : 00,从而形成一张冲突严重程度极高的不可行图面。由打分函数计算得到初始图面的评分约为-7 850 000分,远远低于理论上的最大值(0分)。以这个初始图面为初始状态开始迭代,随着时间步的推移,每次从策略集合中选择一个当前状态下的最佳动作,约300次迭代之后,可以得到一张无冲突的图面,在CPU未满载的情况下这个过程大约需要花费40 min左右。然后,在不引入新冲突的条件下,对图面进行均衡性的优化,大约在1 000次迭代(含之前的300次)之后可得到一张经过充分优化的图面。迭代1 000次得到的图面状态如图3所示,对应的图面打分为-70分,接近于理论上限(0分),在CPU未满载的情况下整个过程可在2 h之内完成。
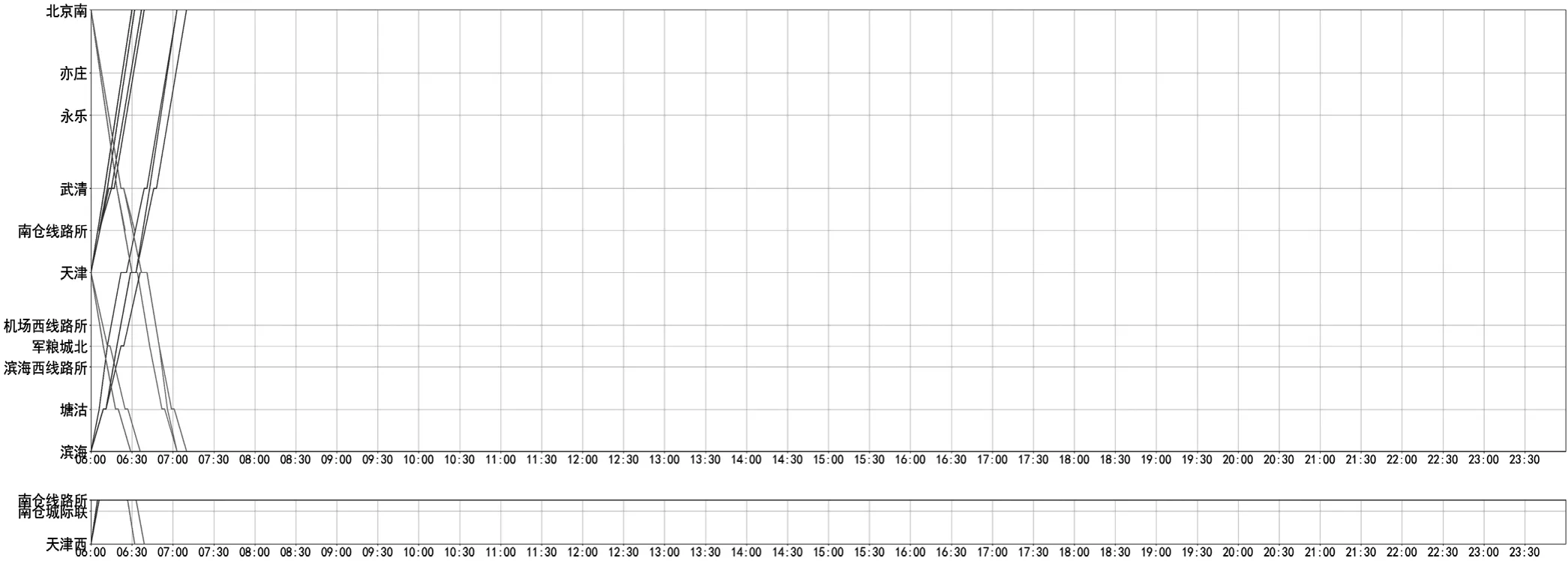
图2 初始图面状态Fig.2 Initial state of the timetable
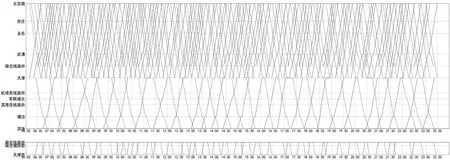
图3 迭代1 000次得到的图面状态Fig.3 State of the timetable after 1 000 iterations
3 结束语
列车运行图的调整优化需要同时考虑铁路运输生产实践中多个部门、多个环节的复杂因素。考虑均衡性的城际铁路列车运行图的调整优化算例,运用人工智能方法,初步探索计划编制阶段的列车运行图调整问题,验证模型方法在解决相对简单的小规模问题场景中的可行性。然而,该模型方法与实际应用还有较大的距离,还应一体化地考虑动车组和车站到发线运用问题,更加全面地考虑旅客出行需求,通过运用该方法解决成网条件下大量跨线列车在长大干线上运行所带来的复杂问题。
