形式各异 本质归一

黄邵华

[摘  要] 已知斜三角形“边边角”解该三角形是高中数学“解三角形”一章中常见的问题，教师在教、学生在学的过程中常会用到“图形法”“正弦定理法”“余弦定理法”三种方法判定解的个数或求具体解. 文章通过计算分析，论证了上述三种方法在判定解的个数的过程中进行分类讨论时的分类标准、分类类型及最终结论上的一致性，并且给出了具体问题中合理选用哪种方法的策略.

[关键词] 解三角形;边边角;作图法;正弦定理;余弦定理

“解斜三角形”是高中数学必修5中的一章，本章内容主要介绍了正弦定理、余弦定理以及这两个定理在解斜三角形等方面的应用. 其中，解斜三角形一般分为这五类问题：“角边角”“角角边”“边角边”“边边边”以及“边边角”问题. 其中前四类问题在有解的前提下则必然有且仅有一个解. 而“边边角”问题（即已知某斜三角形的两边和其中一条边的对角，求三角形的另外一边和两角的问题），则是解斜三角形问题中一种常见的也是易错的题型.

学生在初中学习三角形全等时，已经知道可以通过“角角边”“角边角”“边角边”“边边边”四种方法来证明两个斜三角形全等，到了高中学习正弦定理、余弦定理后，前二者可以优先采用正弦定理入手解三角形，后二者可以优先采用余弦定理入手解三角形. 同样，学生在初中也学习过“边边角”不能够用来证明三角形全等，如果已知某斜三角形的两边和其中一条边的对角，那么该三角形可能会有多少组解、宜使用什么方法来求解，则需要在高中学习正弦定理、余弦定理后才能解决.

高中生在学习解决这类“边边角”问题时，一般会接触到这三种方法：作图法、正弦定理法、余弦定理法. 但是因为知识和时间的跨度等原因，学生在学习过程中却很少会去思考，教师在教学过程中也很少会去提出下面几个问题：这三种方法之间的关联是什么？它们的过程和结论能否统一起来？在具体问题当中应该如何选择方法？本文将对以上几个问题进行阐述.

提出问题：已知△ABC为一个斜三角形，角A，B，C所对的边的长度分别为a，b，c，若a，b及A为已知，解该三角形.

首先，由题中的已知条件，如果仅仅需要判断解的个数，可以通过作图法直观判断，具体如下.

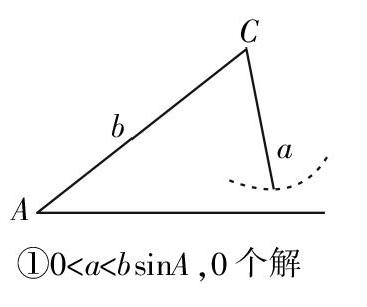
（1）若A为锐角，有以下5种情况：

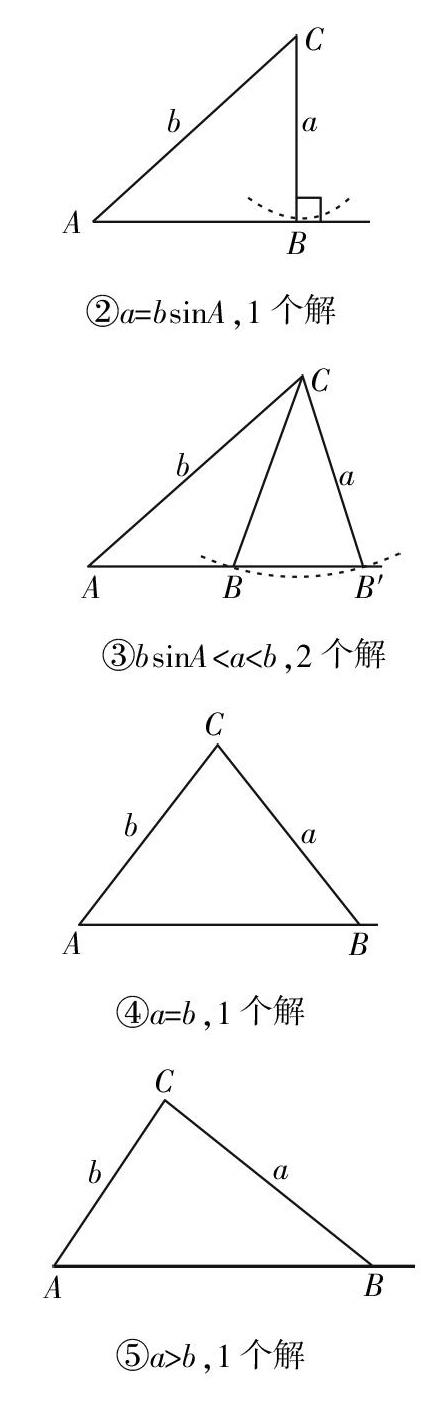
①0

②a=bsinA，1个解

③bsinA

④a=b，1个解

⑤a>b，1个解

（2）若A为钝角，有以下2种情况：

①0

②a>b，1个解

从上述图中可以看到，若A是锐角，只要根据a与bsinA及b的大小关系作为标准进行分类，可以分为5种类型，最终的结果可能是0个解、1个解或2个解;若A是钝角，则只需根据a与b的大小关系作为标准进行分类，可以分为2种类型，最终的结果可能是0个解或1个解.

作图法能够很快判断出解的个数，只是一种定性的判断，如果定量地具体求解角或者边的值，这种方法就无能为力了，此时就需依靠正弦定理和余弦定理来求解.

下面我们分析利用正弦定理求解过程中导致的不同情况是如何系统地与作图法的不同情况一一对应的.

（1）若A是锐角，由正弦定理可得sinB=■.

①若01，B有0个解;

②若a=bsinA，则sinB=■=1，B=■，B有1个解;

③若bsinA

④若a=b，则B=A，B有1个解;

⑤若a>b，则sinB=■∈（0，1），B=B00

（2）若A是钝角，由正弦定理可得sinB=■.

①若a>b，则sinB=■∈（0，1），B只能是锐角，B有1个解;

②若a≤b，则sinB=■≥sinA，则B≥A，B有0个解.

可以发现，利用正弦定理求解的过程中，分类讨论的标准、类型以及结论与作图法是完全一致的. 也就是说，利用正弦定理求解过程中的每一种情况都可以用作图法直观表达，反之，用作图法讨论的每一种情况，都可以通过正弦定理的计算验证.

相比作图法，正弦定理求解除了能够判定解的个数，还能够求出另外一条边的对角的大小，进而通过正弦定理或余弦定理即可解该三角形了.

实际上，在具体问题中，学生还可能用余弦定理来求解，下面我们分析利用余弦定理求解过程中讨论的不同类别是如何系统地与作图法、正弦定理法讨论的不同类别一一对应的.

由余弦定理可得c2-2bcosA·c+b2-a2=0，这是一个关于c的一元二次方程，Δ=4b2cos2A-4（b2-a2）=4（a2-b2sin2A），且两根之和c1+c2=2bcosA，两根之积c1c2=b2-a2.

（1）若A是锐角（cosA>0）：

①若0

②若a=bsinA，则Δ=0，c=bcosA，c有1个解;

③若bsinA0，且c1+c2>0，c1c2>0，因此方程的2个解均为正数，所以c有2个解;

④若a=b，则c2-2bcosA·c=0，c=2bcosA，c有1个解;

⑤若a>b，则Δ>0，且c1+c2>0，c1c2<0，因为c>0，所以c有1个解.

（2）若是钝角（cosA<0）：

①若a>b，则Δ>0，且c1+c2<0，c1c2<0，因为c>0，c有1个解;

②若a≤b，则c1+c2<0，c1c2>0，则c1，c2<0，因为c>0，c有0个解.

从以上分析，我们可以发现，利用余弦定理求解的过程中，分类讨论的标准、类型以及结论与作图法和正弦定理法也是完全一致的. 也就是说，利用正弦定理、余弦定理求解过程中的每一种情况都可以用作图法直观表达，反之，用作图法讨论的每一种情况都可以通过正弦定理、余弦定理的计算验证.

相比作图法和正弦定理求解的方法，采用余弦定理求解除了能够判定解的个数，还能够求出第三条边的大小，进而通过正弦定理或余弦定理即可解该三角形了.

我们将前面的分析汇总成表1，表2.

上述作图法、正弦定理求解法、余弦定理求解法这三种方法，虽然求解的过程完全不同，但通过上述的理论分析，我们可以将他们统一起来理解. 虽然求解过程形式各异，但蕴含的本质归一.

最后，如果我们在遇到具体的“边边角”问题时，该如何合理选用以上三种方法呢？通过上面的分析，我们大致可以做出以下结论：

（1）如果问题仅仅是判断解的个数，可依据实际情况，宜采用作图法或正弦定理进行判断;

（2）如果问题是求某一个角，宜采用正弦定理更便捷些;

（3）如果问题是求某一条边，宜采用余弦定理更便捷些;

（4）如果问题是解该三角形，采用正弦定理或余弦定理均可.