从发展心理学角度看数学抽象素养的培养
2020-09-26王思义朱键
王思义 朱键
[摘 要] 数学抽象作为高中数学的核心素养之首,对于培养学生的整个素养,具有奠基作用. 文章以“向量概念”为载体,结合高中生在逻辑抽象思维方面的发展心理学,分析并阐述了在概念课中培养学生的数学抽象素养的方法. 在教学过程中,应让学生亲历抽象过程,掌握抽象的一般步骤,进而转化为学生的数学素养.
[关键词] 发展心理学;核心素养;数学抽象;向量概念
在2017年版的《普通高中数学课程标准》中明确了高中阶段学生通过数学学习达成的六大数学核心素养[1]. 其中数学抽象位居第一,它应是其他核心素养达成的基础,因为数学中的概念、命题、定理等内容都是抽象的产物,应用数学解决实际问题的模型是抽象而来的. 这些决定了数学的“抽象性”,这也是数学区别于其他学科的最明显的特点;也正是这种“抽象性”,是学生学习高中数学的困难之处. 在2017年版的《新课程标准解读》中指出,“数学抽象素养的培养需要深入到具体的学习活动中去,教师的教学方法的选择要立足于对学生数学学习的心理认知特点和规律的把握,概念、命题、规则、模型乃至思想、方法的获得,本质上是学习者在数学抽象过程中得到心理认知发展的过程.”[2] 本文以“向量的概念”的教学为载体,从发展心理学的角度分析学生数学抽象素养的培养方法.
高一学生的抽象水平发展特点分析
在发展心理学中,认为:整个中学阶段,是学生抽象思维快速发展的时期. “在少年期(主要是初中生)和青年初期(主要是高中生)的思维是不同的. 在少年期的思维中,抽象逻辑思维虽然开始占优势,可是在很大程度上,还属于经验型,他们的逻辑思维需要感性经验的直接支持. 而青年初期的抽象逻辑思维,则属于理论型,他们已经能够用理论作为指导来分析综合各种事实材料,从而不断扩大自己的知识领域.”[3] 也就是说,初中的抽象水平处于由经验型向抽象思维转化,抽象思维占主要部分. 而高中应具备较强的抽象水平,是有很大的提升的. 那么这里的提升,怎么去实现呢?“高中一年级到高中二年级是逻辑抽象思维的发展趋于‘初步定型或成熟的时期.”“成熟前思维发展变化的可塑性大,成熟后则可塑性小,与其成年期的思维水平基本上保持一致,尽管也有一些进步.”[3] 高一的学生,应该是学生从初中向高中转型时期,那么这种抽象能力的提高,应该是在教师的引导下进行的. 因此,我们教师就应抓住这一关键期,培养学生的抽象能力,使得学生尽快地适应高中学科知识的学习,也是完成抽象能力的提过的过程的关键时期. 在2017年版的《新课程标准解读》中,专家们建议教师们在平时的教学中,让学生经历数学抽象的过程,掌握数学抽象的方法[2].
但是,在高中课堂,一些教师在教学中,并没有让学生去完成抽象过程,而是自己举例,自己抽象,给出定义,对定义的内涵跟外延的阐述,进行相关题目的训练. 这样就使得学生虽然掌握了一定的数学知识,但不知道为什么要学习这些内容,应该怎样学习这些内容. 大大地影响了学生应用数学的能力. 数学中的概念课,应该是数学抽象的大本营. 我们如果在教授概念时,让他们经历抽象的过程,教会他们抽象思维的方式,那么在高中众多概念的学习中,学生就会形成一个研究系统. 自然地,学生的抽象能力也就会形成理想效果.
笔者听过关于“向量概念”的一些公开课,教师们对这个课题进行同课异构,但效果都不是很好. 一部分教师拿到这个课题,就不知道这节课怎么上好,因为这节课概念难度不大,概念较多. 居多都是按照课本内容去上,稍微好一点的,也就是在抽象向量概念前的例子选取上下了一些功夫,但对于学生的抽象能力的培養意识比较薄弱. 下面,以培养学生数学抽象思维的角度,对“向量概念”这一节课进行教学分析和教学设计.
向量概念的抽象过程
所谓抽象是指:“从具体事物中抽取相对独立的各个方面、属性及关系等的思维活动,抽象的结果具有一定的‘抽象性,与具体事物的‘具体性相对立. ”[4]所谓数学抽象是指:“通过对数量关系与空间形式的抽象,得到数学研究对象的素养.”[1]关于数学抽象,史宁中先生在他的两本书《数学抽象:数量与数量关系》《数学抽象:图形与图形关系》有关于抽象过程的详细阐述. 在《数学抽象:数量与数量关系》一书中,对人类对数量的抽象的过程进行了阐述. 我们可以从中看出数量的抽象过程是漫长的. 我们在教学中,课本上的内容的编排是按照知识逻辑顺序来编排的. 而我们教学时,教师应将这一思维过程呈现给学生. 当然,这过程中,不是完全放手,由学生天马行空地去想,而是教师应起到一个引路人的作用. “向量概念”的抽象也应体现这一思维过程,并且让学生经历这一过程. 史宁中先生将抽象分为三个层次:“①把握事物的本质,把繁杂问题简单化、条理化,能够清晰地表达,我们称其为简约阶段. ②去掉具体的内容,利用概念、图形、符号、关系表达包括已经简约化了的事物在内的一类事物,我们称其为符号阶段. ③通过假设和推理建立法则、模式或者模型,并能够在一般的意义上解释具体事物,我们称其为普适阶段.”[5]
1. 数学抽象中的简约阶段
对于“向量概念”,首先应该是向量的抽象,把握本质,就应从大量的实例中提出数学本质.
教师举例:向同学问路“到校门口怎么走”.
学生回答:从教室往前走.
教师:就这样我就能找到校门口了吗?
学生:500米处.
教师:路牌上的路标也是这样,标有到某某地方的方向和距离. 汽车上的导航,经常会提醒我们到某个地方,沿着某一个方向行驶多远的距离.
教师:我们学的这一章的章前图,小船航行的航线,有距离,有方向.
教师:在这些例子中,说明我们要找到确切的位置,需要哪些要素?
学生:距离、方向.
教师:位置在我们物理上称为什么呢?
学生:位移.
教师:说明“位移需要用大小和方向来表达”. 物理上还有哪些像这样的例子呢?
学生:速度、加速度.
教师:对,也就是这些量,我们不仅关心它的大小,还要关心它的什么?
学生:方向.
教师:这样的量,我们在数学里见过吗?我们以前学习的量是什么?
学生:大小.
教师:对,也就是数量.
教师:物理中的位移、速度、加速度,这些对象在我们数学上,用数学的眼光去看,是新的问题. 从数学角度来看,它们有什么共同的地方?
学生:它们都有大小、方向.
教师:对,这是我们以前在数学中没有研究的问题. 今天我们就来研究它. 既然这个量是具有方向的量就给它一个名称“向量”.
这里学生经历了从具体到抽象的过程. 感受到抽象,实际就是找出不同事物之间的数学本质特征. 那么这里就完成了史宁中先生讲的第一步:简约阶段. 这里教师应将这一步的抽象阶段和方法告诉学生.
教师:我们以上的过程,就是从众多的事物中,提炼出它们在数量关系与几何关系方面的共有的本质特性.
这一步,我们称其为简约阶段. 也就是抛开繁杂的事物背景,找出数学共性.
2. 数学抽象的符号阶段
接下来,就是第二步:符号阶段. 教师应向学生讲解清楚抽象的第二个步骤为符号阶段.
教师:抽象的第二步:符号阶段. 只有对向量赋予一定的符号,才能用数学的方法对它的性质、计算等方面做进一步研究. 那么我们用什么符号来表示向量呢?
学生应该不难发现导航上用有向线段表示,物理上也是用有向线段表示的.
学生:有向线段.
教师:对,我们这里的表示方法和物理上的统一:有向线段. 用两点A,B分别表示起点、终点. 由起点指向终点的有向线段. 有向线段的长度表示向量的大小,方向表示向量的方向. 向量的字母上面加上箭头■,这是向量的图示方法. 向量的大小称为向量的模长,简称模,记为■.
这和学生平时的认知习惯相符,让学生接受起来也不难.
教师:当我们有了研究对象的几何表示和字母表示,我们就可以从几何和代数的角度,较为简洁地去研究它,也就是我们前面提到的符号阶段.
有了符号表示后就可以对向量性质和计算进行抽象.
教师:在一个数学系统中,我们需要规定它的零元和单位,数量中0表示没有,1表示一个单位,那么向量中也应该规定零向量和单位向量,应该怎么规定呢?
学生:模长为零的向量为零向量,模长为1的向量称为单位向量.
教师:我们分别把零向量和单位向量记为:0,e.
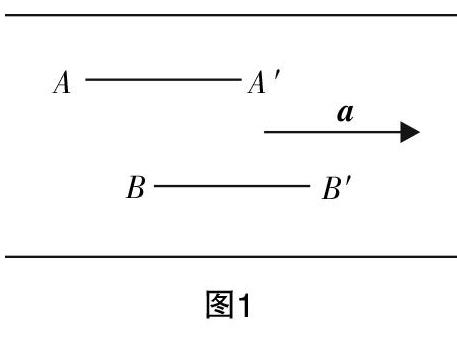
教师:为了研究向量的性质,这里我们来看一个例子[6]:两个小船,分别从A与B点出发,在水流的作用下都向东行驶,在相同的时间内行驶到A′和B′点. 它们的位移用什么表示?
学生:可以用向量■和■表示.
教师:这里小船的位移实际上是什么作用的效果?
学生:水流.
教师:作用在两个小船上的效果是否相同??摇?摇
学生:相同.
教师:所以向量■和■相同吗?
学生:相同.
教师:那么向量■和■的起点不同,但方向相同,大小相同,这两向量是相同的,这说明向量具有什么样的性质?
学生:向量与起点无关.
教师:也就是,向量的大小相同,方向相同,我们就把它们视为同一个向量,也就是相等的,记为:■=■. 我们把与起点无关的向量称为自由向量. 我们这里学习的向量不需要考虑起点,所以我们所说的向量都是自由向量.
教师:数量即多少■,向量由于既属于代数对象,又有几何特征,所以我们不能笼统地比较向量的大小. 但我们可以分开来讲,对于代数特征,我们可以比较它们的什么?
学生:模长.
教师:几何特征呢?
学生:方向相同或相反.
教師:我们把方向相同或相反的两个非零向量称为是共线的,记为:■∥■. 因为它们可以平移到同一条直线上. 书上的例1[7]作为这部分内容的巩固掌握.
向量的性质抽象之后,就应该是向量的计算的抽象.
教师:下一节课,我们继续对向量的抽象,向量计算的抽象.
3. 数学抽象的普适阶段
这里对于向量概念抽象的普适阶段应该是后面的,应用“向量法”解决几何与代数问题. 虽然课时不够了,但我们在这里应该向学生介绍,因为这三个步骤,它们是一个整体,让学生知道数学抽象的完整的步骤.
教师:向量有大小,属于数学上的哪个分支?
学生:代数.
教师:向量有方向,属于数学上的哪个分支?
学生:几何.
教师:那么向量既属于代数又属于几何对象,向量也就自然地成为沟通代数和几何的桥梁.
教师:在后面的学习,我们借助“向量”,用代数的方法解决几何问题,用几何的方法解决代数问题. 也就是抽象的第三步:普适阶段. 研究向量的性质、计算之后,用它研究其他对象. 这就是普适阶段. 这个内容放到后面来讲.
最后的小结部分,应让学生总结数学抽象的步骤. 这一节课,不仅要学习向量的知识,更应该让学生经历抽象的过程,让他们掌握数学抽象的一般方法. 这样,在学习高中的众多抽象的概念时,学生可以根据一定的认知策略进行自我探索,相应地降低了高中数学学习的难度.
参考文献:
[1] 中华人民共和国教育部制定. 普通高中数学课程标准(2017年版)[S]. 北京:高等教育出版社,2018.
[2] 史宁中,王尚志. 普通高中数学课程标准(2017年版)解读[M]. 北京:高等教育出版社,2018.
[3] 林崇德. 心理学[M]. 杭州:浙江教育出版社,2002.
[4] 徐利治,郑毓信. 数学抽象方法与抽象度分析法[M]. 南京:江苏教育出版社,1990.
[5] 史宁中. 数学思想概论:数量与数量关系的抽象(第1辑)[M]. 长春:东北师范大学出版社,2015.
[6] 徐元根. 对中学向量概念叙述方式的建议[J]. 中学数学月刊,2001(11).
[7] 人民教育出版社中学数学室. 全日制普通高级中学教科书(必修)数学第一册(下)[M]. 北京:人民教育出版社,2003.
