自主建构 深度反思

张居敏 瞿兵

[摘  要] 文章以“任意角”教學设计为例，从概念产生的“必要性”、推广的“合理性”及与主题教学内容的“统一性”进行教学实践，既建立了任意角的概念，更提炼出建构新概念的一般过程与原则，深化学生自主建构概念的意识.

[关键词] 必要性;合理性;统一性;概念教学

概念生成“三个层次”的确立

概念是事物本身的反映，数学概念的教学，必须反映数学对象的本质属性和基本特征. “任意角”是高中三角函数内容的起始课，属于概念教学，揭开了“任意角的三角函数”学习与研究的序幕.

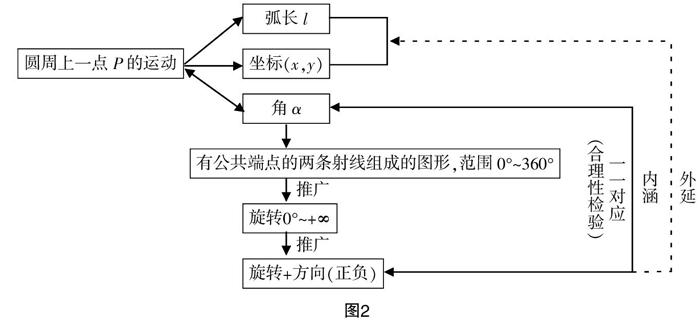
学生通过章首引言部分的学习，明确了本章基本问题“圆周上一点的运动”，并由此引发了中心问题：在表示点P的过程中，我们先后选用角、弧长和直角坐标，那么α，l，x，y等元素之间有着怎样的内在联系？

作为概念起始课，在设计上应体现出其被赋予的理论“高度”. 随着基本问题的明确和中心问题的提出，“任意角”的教学就不能简单地从“规定”层面出发. 由其本质属性，应从其概念产生的“必要性”、概念推广的“合理性”及其与三角函数这一主题教学内容的“统一性”这“三个层次”进行教学与实践，让学生“像数学家一样去思考问题”成为思维线索，通过对“角的概念的推广”的探究过程，既建立了任意角的概念，更提炼出建构新概念的一般过程与原则，可深化学生自主建构概念的意识，提升自主完善概念及反思的能力.

概念生成“三个层次”的实践

1. 情境引入——体验“必要性”

“圆周上一点的运动”是本章的基本问题，因此，在情境引入环节，笔者采用摩天轮这一圆周运动的模型，提出如下问题：

问题1：摩天轮的半径为6米，从水平位置A出发，转动一圈需6分钟，请用一个量来刻画一分钟后点P的位置.

学生活动：通过启发，学生回答可用60°角、弧AP、以O为圆心OA所在直线为x轴建立坐标系后点P的坐标这三种方式来刻画其位置. 学生用“角度”较易地刻画了点P的位置，而用其他刻画方式在数值计算上均存在一定困难.

设计意图：此问题的提出既引出了“角”这一刻画圆周运动的模型，引领学生对其概念进行了回忆和思考，同时也在学生心中埋下了“多种不同的刻画方式描述同一事物，它们之间必然存在某种联系”这粒“种子”，为之后概念的“统一性”探究埋下了伏笔. 而接下来的研究围绕学生最熟悉的“角”展开也就顺理成章了.

问题2：摩天轮的半径为6米，从水平位置A出发，转动一圈需6分钟，请用一个量来刻画8分钟后点P的位置.

学生活动：学生回忆初中对于角的定义为：从同一点出发的两条射线组成的图形，范围是0°～360°. 此定义无法刻画8分钟后点P的位置，因此，必须对角的概念进行推广.

设计意图：问题2的提出，让学生体会之前对于“角”的定义的“不合理”性及对于“任意角”定义产生的必要性.

基于对现实对象关系或数学逻辑结构的抽象产生认知冲突或需求，是一种研究过程所遇到的困境，是概念生成的必要性. 笔者通过创设认知冲突，引导学生对概念产生的“必要性”进行分析，使学生发现问题、提出问题，也为后续的解决问题提供了依据.

2. 概念生成——探索“合理性”

对于问题2，通过教师引导及摩天轮这一充分体现了“旋转”的模型，学生利用“旋转”对其进行动态定义，并将角的范围推广至0°～+∞.

问题3：摩天轮的半径为6米，从水平位置A出发，转动一圈需6分钟，已知∠AOP=90°，请画出点P的位置.

学生活动：无法确定点P的位置，刚刚的定义推广还不够合理，还需要规定旋转方向.

设计意图：通过问题2和问题3的提出，分两步对原有角的概念进行推广，既体现了推广的“必要性”，更通过引导学生进行反思，不断检验推广的“合理性”.

通过两次对原有定义的“合理性”反思，逐步提炼出任意角概念中的两个要素：“旋转量”与“旋转方向”.

问题4：对于角的定义，旋转量与旋转方向两个要素足够了吗？为什么？你能给出角的定义吗？它合理吗？

学生活动：经过引导，学生体会到对于给定一个旋转量和旋转方向，能画出唯一的角;同时，对于一个给定的角，也有唯一的旋转量和旋转方向与之对应. 因此学生体会到了角与这两个要素是“对应”的，这样的定义就具备了“合理性”的要求.

设计意图：为了能解决存在的冲突和需求，我们推广了角的概念，仍需对其进行检验或论证，探索概念生成的合理性. 对新定义的概念进行检验和论证应是对新概念产生之后的必经过程，这不仅是数学问题研究的过程，更是一种理性的思维精神，是一种敢于质疑、善于思考、严谨求实的科学精神.

以上过程可由图2表示.

3. 概念反思——“统一性”体会

问题4的解决，学生初步建构了“任意角”的概念，并从定义中提炼出“旋转量”与“旋转方向”两个要素对其进行合理性检验，从内涵的角度来说，角与刻画方式之间形成了一一对应，那这是不是概念“合理性”的唯一要求呢？

回到本章的中心问题：在表示点P的过程中，我们可以选用角、弧长和直角坐标，那么α，l，x，y之间有着怎样的内在联系？

从外延的角度来看，若“任意角”的定义是合理的，那其必然能与三角函数这一整体数学内容相“统一”. 虽然本节课无法研究此内容，但学生心中的这粒“种子”，会在弧度制产生“必要性”与“合理性”的学习探究中“生根发芽”.

对“统一性”的体会，本质是对概念建构“合理性”的一种外延检验，也可认为是章首引言部分的一段教学延伸. 此段教学内容，通过师生对话的形式展开，不为得到某个确定的结论，旨在启迪学生的思维，将知识的逻辑结构和学生的思维方式结合起来，以研究问题的一般方法为暗线，从而将研究问题方法内化为学生的认知结构.

對于新概念的教学，以概念生成的三个层次为脉络进行教学设计，根据学生已有的认知基础和经验，以“必要性”为出发点，不断优化推广新的概念形式，通过对其“合理性”与“统一性”的检验分析，形成概念的准确表述，理解其内涵与外延.

概念生成“三个层次”的递进

基于对概念基本特征的思考，我们还需对新建构的概念进行“表达”与“量化”，由此产生对象限角与终边相同角的教与学.

问题5：当我们建构了“任意角”的概念之后，我们该做什么？

生：我们该对其进行量化研究.

问题6：如何研究？

（师生互动）

师：一堆杂乱放置的笔，如何比较其长度？

除了度量之外，学生提出最快的方法是将这些笔“共起点”（即一端处于同一平面，比较另一端的高度），便能快速比较其长度.

师：那对于角而言，是否可将此方法进行迁移，除了度量之外，如何方便研究呢？

生：也让角“共起点”.

师：何为“共起点”？

生：角的起点可认为是其始边，因此我们可以将角的顶点作为坐标原点，角的始边作为x轴正半轴，建立平面直角坐标系.

设计意图：中心问题的提出对“象限角”概念的产生有正迁移的作用，定性分析之后随之而来的便是定量研究. 在此“表达”与“量化”的递进环节，教师只有在教学过程中重生成、重联想、重类比，才能让学生学会思考、懂得思维.

问题7：对于之前摩天轮的例子，大家还能提出什么不一样的问题吗？

学生活动：之前的问题都是由旋转的时间确定点P的位置，因此可以提出：已知点P的位置，能否确定旋转的时间？

问题8：“终边相同的角”具有哪些形的特征，又该如何用数学语言来描述呢？

学生活动：形的特征为相差k圈，数的特征为相差360°的k倍，我们可用集合表示.

设计意图：爱因斯坦曾说过“提出一个问题，往往比解决一个问题更重要”，因为解决一个问题，也许仅仅是一个数学上或实验上的技能而已，而提出新的问题、新的可能性，需要从新的角度去看旧的问题，需要有创造性的想象力，而且标志着科学的真正进步.

让学生从反面提出问题，建构解决这一问题的基本模型——终边相同的角，并用数学语言刻画，逐步解决了本节课的难点.

苏联数学教育家斯托利亚尔曾说过“积极地数学教学，应为数学活动（思维活动）的教学，而不是数学活动结果——数学知识的教学”.

让学生体会概念产生的必要性，在概念生成的过程中学会数学语言的提炼与表述;让学生在丰富的感性思维的基础上，主动地进行去粗取精、由表及里的改造，理解概念的合理性;更提炼出了建构新概念的一般过程与原则，发展学生的科学精神、理性精神、创新精神. 这些取代了知识本身成为本课教学设计的线索和主旋律. 笔者在本节课的设计上努力实践美国教育家苏娜丹戴克说过的一句话：“Tell me， I will forget; Show me， I may remember; Involve me， I will understand.”（告诉我，我会忘记;做给我看，我会记住;让我自主参与，我会完全理解. ）