运用图形语言,提升解决问题能力
2020-09-26郎佳
郎佳
[摘 要]图形语言、文字语言是数学语言的重要组成部分,在理解文字语言遇到困难时,可以把文字语言转换为图形语言。图形语言具有直观、形象等特点,能够激活学生的思维,有利于学生理解与分析问题,帮助学生寻找到正确的解题思路,提高学生解决问题的能力。
[关键词]图形语言;提升;解决问题能力
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2020)30-0033-02
数学语言是数学思维的载体,数学学习实际上是数学思维活动的过程。数学语言具有高度的抽象性、严密的逻辑性和应用的广泛性等特点,能够以简洁的文字抽象出事物的特征,表现出事物之间的内在逻辑和联系。小学生的思维以直观形象思维为主,而数学问题通常采用文字语言和符号语言进行表述,所以学生的思维有时会陷入困境,出现思维空白或者思维混乱等情况。数学语言转换的方法和原则比较简单,掌握转换机制,将文字语言和符号语言转化为图形语言,可以帮助学生顺利地分析与解决问题,提高学生解决问题的能力。
一、借助图形语言理解题目意思
理解题目意思是解决问题的第一步,然而理解题目意思并不等同于读题,能够找到题目中的关键信息、明确所问问题、不看题目也能复述题目的意思,这才算理解了题目意思。可有些数学题目较长,涉及的数学信息比较多,需要读几遍才能够理解题目的意思。这时,教师可引导学生将数学的文字语言转换为图形语言,帮助学生理解题目意思,寻找到解题路径。
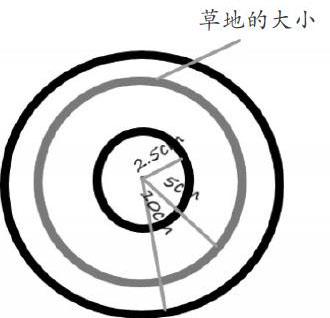
例如,有这样一道典型的数学题:“一片周长是62.8米的圆形草地,准备为它安装一个自动旋转喷灌装置,现有射程为20米、10米、5米三种喷灌装置,你认为选择哪种比较合适?安装在什么地方?”草地灌溉与学生的实际生活联系不大,所以学生读题后不能准确地理解题中的专业名词“射程”,进而产生以下问题:(1)射程不同会有什么后果?(2)如何理解圆形草地上旋转喷灌装置的射程呢?(3)怎样选择合适的射程呢?(4)为什么还要问旋转喷灌装置安装在哪里呢?这时,教师可引导学生将此题转化为图形语言:“先画出圆形草地,题中说圆形草地的周长是62.8米,根据圆的周长计算公式C=2πr,求出圆形草地的半径为10米。”由于草稿纸有限,教师让学生进行等比例缩小,画出半径为5cm的圆。“题中说旋转喷灌装置用来浇灌圆形草地,并特意强调‘旋转二字。也就是说,如果知道一个圆的半径,将半径沿着顺时针方向或逆时针方向旋转一周,就可以画出一个圆。那么,题中的射程就是告诉我们,旋转喷灌装置喷洒的半径有20米、10米和5米这三种选择。”然后教师让学生以草稿纸上“草地”的中心为圆心,分别画出半径为10cm、5cm、2.5cm的圆。“通过画图(如下)可知,半径为2.5cm的圆的面积小于半径为5cm的圆的面积,如果选用射程为5米的旋转喷灌装置,草地就不能够得到完全灌溉,所以此射程不适合;半径为10cm的圆的面积要远远大于半径为5cm的圆的面积,如果选用射程为20米的旋转喷灌装置,就会造成水资源浪费;而10米射程的旋转喷灌装置正好可以完全灌溉整片圆形草地,因此选择此射程,并把旋转喷灌装置安装在草地的中心。”这样画图分析之后,学生的思路变得清晰、明朗,最后正确地解答问题。
二、借助图形语言表征数量关系
寻找题中的数量关系是解决数学问题的关键。可在实际学习中,很多学生解决不了数学问题,不是寻找不到题中隐藏的数量关系,就是找错了题中的数量关系。为了提高学生解题的速度和正确率,教师可引导学生用图形语言去表征题中的数量关系,这样既有利于学生快速找到题中的数量关系,又有助于学生分析与解决问题。
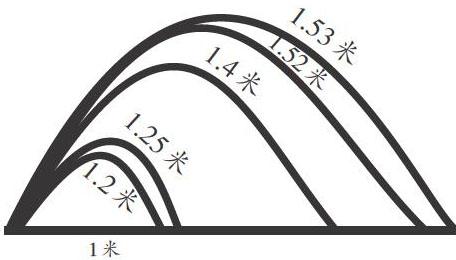
例如,有这样一道数学题:“小红五岁的时候,爸爸给她量了一次身高,当时小红身高为1米。为了让小红知道自己的身高变化情况,小红爸爸连续五年记录了小红的身高。在今后的五年中,小红的身高分别为1.2米、1.25米、1.4米、1.52米、1.53米。小红第一年和第二年分别长高了多少米?第二年比第一年少长高多少米?”初读题目,有些粗心大意的学生是这样解答的:小红第一年和第二年分别长高了1.2米与1.25米;第二年比第一年多长高了1.25-1.2=0.05(米)。显然,学生错误分析题中的数量关系,忽略了题中的一个已知条件——小红五岁时的身高为1米。这时,教师可引导学生画图:“看看将题目转换为图形语言后,会不会有一些新的收获。首先,画出一条线段,表示小红五岁时的身高,并在线段下面标注‘1米;接着,在延长线上画出第二条线段,连接第一条线段的起点和第二条线段的终点后标记‘1.2米;然后连接第一条线段的起点和第三条线段的终点,标记‘1.25米……以此类推,分别标注出小红六年来的身高。”这样画图(如下)后,学生可以清楚地看到:小红第一年长高的高度等于六岁时的身高减去五岁时的身高,即1.2-1=0.2(米);小红第二年长高的高度等于七岁时的身高减去六岁时的身高,即1.25-1.2=0.05(米);小红第二年比第一年少长高的高度等于第一年长高的高度减去第二年长高的高度,即0.2-0.05=0.15(米)。如果不画图的话,除非是逻辑极为严密的学生才能够正确解答这道题,否则大部分学生都可能落入出题人的“陷阱”。因此,解答这道题,把题中的文字语言转换为图形语言,能收到事半功倍的效果。
三、借助图形语言显现思维过程
学生间客观存在个体差异,不仅表现在学习能力上,还表现在思维方式上,所以不同的学生看待和思考事物的方法是不一样的。因此,数学课堂中,教师应激活学生的思维,引导学生借助图形语言分析与解决问题,帮助学生树立学习数学的信心,让学生真正爱上数学这门课程。
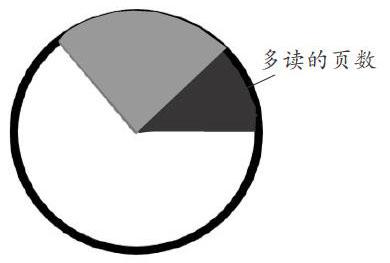
例如,有这样一道数学题:“小红读一本书,第一天读的页数与未读的页数的比是1∶3。第二天读了120页,这时已读的页数与未读的页数的比是2∶3。这本书有多少页呢?”读题思考后,学生想到了兩种转换成图形语言的方法。生1的思路是这样的(如下图):“先画一个圆表示整本书的页数,由于题中告知‘第一天读的页数与未读的页数的比是1∶3,也就是说第一天读了整本书的1/4,所以将圆的1/4涂色;题中又告知‘第二天读了120页,这时已读的页数与未读的页数的比是2∶3,那么此时已读了整本书的2/5,于是把圆中的2/5标注出来。由于2/5-1/4=3/20对应的就是多读的120页,所以可以算出书的总页数为120÷3/20=800(页)。”
生2的思路是这样的(如下图):“已知‘第一天读的页数与未读的页数的比是1∶3,所以我画出一条线段表示已读的页数,又画出第二条线段表示未读的页数,第二条线段的长度是第一条线段长度的3倍;题中说‘第二天读了120页,这时已读的页数和未读的页数的比是2∶3,那么就标记上‘120页,此时便能够找到题中的数量关系了,最后列方程求解。设第一天读的页数是x,那么(x+120)÷(3x-120)=2/3,解得已读的页数为200页,所以整本书总的页数为800页。”
从中可以看出,画的图形不同,解答的方法也不同:生1注意到已读页数和整本书页数之间的比例,而生2注意到已读页数和未读页数之间的比例。因此,教师引导学生用图形语言分析问题时,应给予学生独立思考的空间,让学生展示交流自己的解题思路,这时可能会涌现出新的解题方法。如果新的解题方法可行并且较为实用的话,教师也可以鼓励其他学生使用这种方法,因为数学教学最重要的目标是促进学生个性化、多样化的发展。
总之,在不同的情况下使用图形语言,可以获得不同的效果。数学课堂中,教师应让学生明白图形语言的特点和优势,注重培养学生的数学思维,引导学生学会把握时机、合理选择解题策略,使学生在数学学习上得到更好的发展。
[ 参 考 文 献 ]
[1] 徐燕.数学语言的理解与转译教学[J].小学数学教育,2017(10).
[2] 何英飞.巧用图形语言 扩展数学思维[J].课程教育研究,2017(21).
(责编 杜 华)
