椭球粒子声辐射力计算及分析
2020-09-24王明升欧阳杰崔自宪
王明升 欧阳杰 刘 浩 崔自宪
(1 杭州应用声学研究所 杭州 310012)
(2 中国船舶工业系统工程研究院 北京 100094)
0 引言
当声波在传播过程中入射到目标物上,目标物会产生反射、折射、透射等各种物理现象,这代表着声波与目标物进行能量和动量的交换,因此在实际表现中,粒子将表现为受到力的作用以至于粒子的运动状态将发生变化。一般情况下,粒子受到的力正比于声压的平方。在线性声学范围内,当一列声波入射到材料表面,表面受到的平均(时间平均)压力为零(由于正负抵消),而如果考虑声的非线性,材料表面受到一个不为零的平均压力(非线性声压的“直流”部分),成为声辐射压力[1]。因此通过研究目标粒子的声辐射力(Acoustic radiation force,ARF)特征,可以实现对粒子的运动状态控制,这在目前的生物工程领域和医学领域具有极高的应用价值和广阔的发展前景。
声辐射力的概念最早起源于光学,并且光波粒子操控在当今社会的粒子操控和捕获方面已经得到了广泛的应用。Ashkin[2]首先提出了光镊子的概念,通过利用激光的辐射压力,可以对微小的原子和分子进行捕捉和操控。由于声波和光波的物理特性十分接近,国内外学者将粒子操控研究从光波逐渐转为声波。声辐射力的理论研究于20世纪30年代就已经开展,King[3]首先提出了声辐射力的概念,并且完备、系统地介绍了声辐射力的推导过程和计算公式,这为未来其他学者对声辐射力的特性进一步讨论研究奠定了坚实的理论基础。稍后,Hasegawa 等[4]推导并计算出水下弹性球的声辐射力的特征曲线,以及黏弹性球的声辐射力的物理特征[5]。起初,Marston[6]将Bessel波束引入到声学领域,发现了Bessel波束作用于水下目标物的独特特性,因此也逐渐研究Bessel波束对粒子的轴向声辐射力的作用。液体球在较大波锥角的零阶Bessel波束作用下容易产生负方向的声辐射力,Marston将此归因于粒子的背向散射受到极大的抑制。对于负声辐射力的产生,Zhang 等[7]从数值角度进一步分析负声辐射力的产生机理,当ω>cosβ时将会有负声辐射力产生。惠铭心等[8]采用分波序列(Partial wave series,PWS)的方法推导了多个稀疏分布的粒子声辐射力,认为只需要分别计算各个双粒子系统的声辐射力就可以通过叠加得到声场中任意粒子的声辐射力。但是,目前对声辐射力的研究主要集中于球形粒子,对椭球粒子声辐射力研究缺少,尤其是液体椭球粒子声辐射力的研究。
本文根据声散射理论,采用分波序列方法进一步推导了椭球粒子在任意波束照射下声辐射力函数的解析表达式,拓展了分波序列方法的应用范围,研究了不同介质的椭球粒子在不同入射波束作用下声辐射力的分布特点,为利用粒子的外形和介质进行声学操控提供了理论依据。
1 理论推导
如图1所示,零阶Bessel波束在理想流体介质中照射椭球粒子。在理想流体介质中的入射声场可表示为
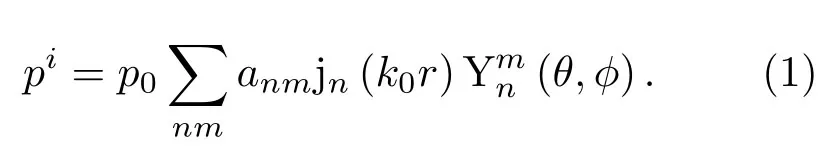
当波束照射到水下目标物后,流体介质中将被激发出散射声场,散射声压可表示为
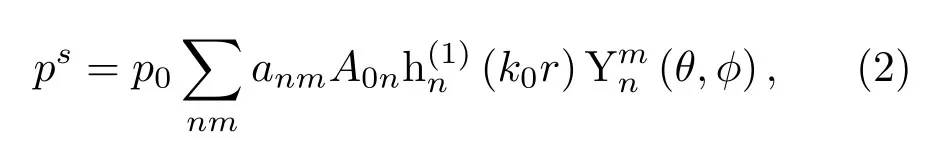
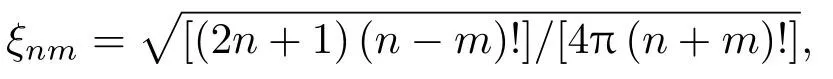
由于本文讨论的是椭球粒子在Bessel波束照射下,其声辐射力的特征,在理想流体介质中,Bessel波束的入射分波系数可表示为[9]
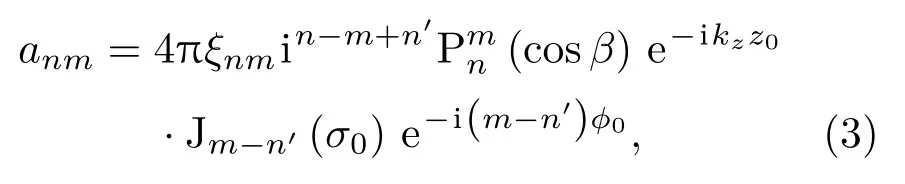
其中,β表示入射Bessel波束的波锥角,Jn′(·)表示n′阶柱Bessel函数,kr=k0sinβ和kz=k0cosβ分别表示径向和轴向方向的入射波波数,入射Bessel波束的坐标位置为(x0,y0,z0),σ0=krR0,本文中将主要讨论椭球粒子在Bessel波束轴向入射情况下声辐射力特征,因此Bessel波束位置为(0,0,0)。
本文将讨论刚性椭球粒子和液体椭球粒子的声辐射力特征,由于液体椭球粒子与周围流体介质阻抗差异很大,液体椭球粒子即可认为是刚性椭球粒子。基于液体椭球粒子能包括刚性椭球粒子的原因,所以下面将介绍液体椭球粒子的推导过程。
对于液体椭球粒子内,其入射声场表达式为

其中,B0n表示椭球液体介质内入射波的无量纲分波系数,k1表示椭球液体介质内入射波波数。
图1已经给出了椭球粒子的物理模型,其外形的表达式为
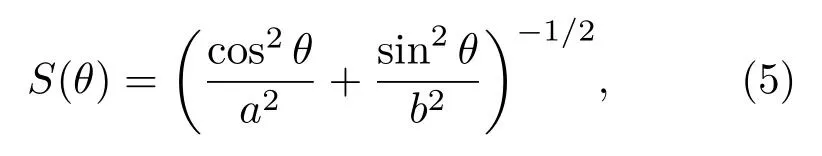
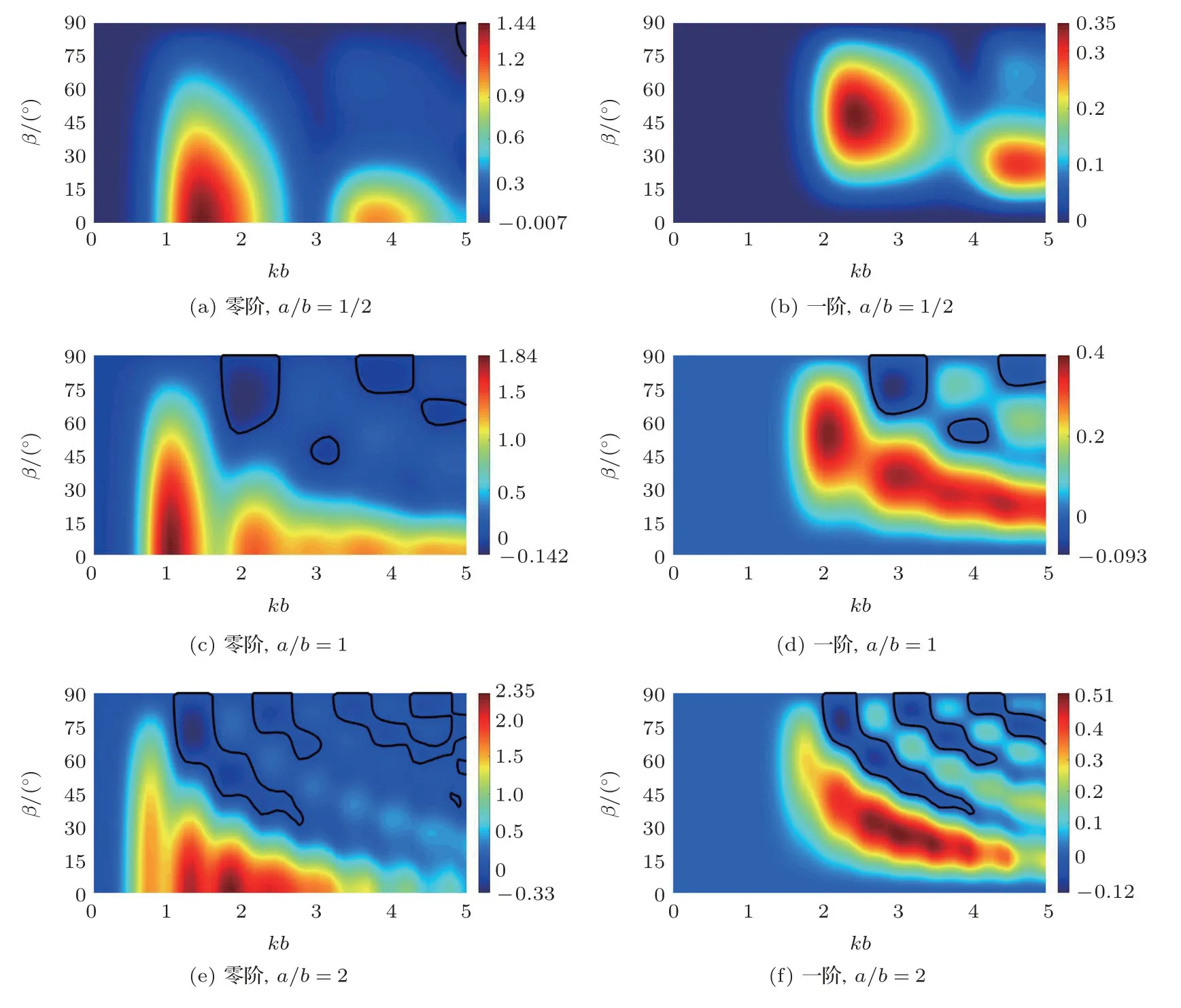
其中,a为椭球体的极半径,b为椭球体的赤道半径。从式(5)中可发现,该椭球体的外形表达式S(θ)只与散射角θ有关。当a >b时,该椭球是细长椭球;当a 对于液体椭球粒子和周围理想流体介质,其表面的边界条件是声速连续边界条件和声压连续边界条件,即 图1 零阶Bessel波束入射椭球粒子Fig.1 The spheroid illuminated by the zeroth order Bessel beam 将式(1)、式(2)和式(4)代入式(6)和式(7),可得到声场的表达式为 其中,Γnm(θ,ϕ)、Λnm(θ,ϕ)、Xnm(θ,ϕ)、Enm(θ,ϕ)、Φnm(θ,ϕ)和Hnm(θ,ϕ)的关系分别为 将式(12)代入式(8)和式(9),可得 其中, 根据以上推导的公式,可求得液体椭球粒子在Bessel波束照射下周围流体介质散射波的无量纲分波系数A0n。但是,与液体椭球粒子的边界条件不同,刚性椭球粒子的边界条件是Neumann 边界条件[10]。 声辐射力为一个周期内粒子的平均辐射应力张量对粒子表面的积分,根据文献[11]可知,椭球粒子的轴向声辐射力函数为 其中:Sc代表椭球粒子截面部分的面积,对于标准球形粒子,Sc=πa2;对于细长椭球粒子和扁平椭球粒子,Sc=πb2。snm=anmA0n是散射波的散射系数, Yz表示声辐射力函数,即代表声辐射力在单位声能量密度和单位截面面积下的声辐射力的幅值。由于本文中只讨论Bessel波束轴向入射的情况,因此可知Yx=0和Yy=0。 上文中已经推导了液体和刚性椭球粒子的声辐射力公式,下面将检验以上推导的公式正确性。对于空气中的水滴,由于其两种介质的阻抗差异很大,因此此时可认为水滴是刚性介质。以空气中的椭球水滴粒子为例,空气的密度为ρ0=0.00129 kg/m3,声速为c0=340 m/s,水的密度为ρ1=1000 kg/m3,声速为c1=1480 m/s。另外,无论是刚性椭球粒子和液体椭球粒子,其远场散射形态函数可表示为 其中,r0=max(a,b)。 为了验证椭球粒子的声辐射力函数的正确性,图2给出了空气中水滴椭球粒子在零阶Bessel波束和一阶Bessel波束入射下轴向声辐射力函数,其结果与文献[12]和文献[13]的结果完全一致,说明了以上推导公式的正确性。对于粒子负声辐射力的产生原因,可通过图3对比可知。图3给出了细长椭球粒子在一阶Bessel波束(β=75◦)入射下,入射频率分别为kb=1.6和kb=2的散射形态函数,从图中观察可知当粒子的背向散射受到极大的抑制时,即粒子的前向散射轴向投影的分力大于粒子背向散射轴向投影的分力,根据牛顿第三定律,粒子将会产生背向的运动的合力,因此粒子将产生负声辐射力的效果。 根据轴向声辐射力Fz的推导公式[7], 其中,〈cosθ〉表示对整个散射角度取平均。对于无能量吸收的粒子,当〈cosθ〉>cosβ时将会有负声辐射力产生,并且〈cosθ〉与粒子的外形、介质等存在很大的关系。因此在下文讨论中,刚性椭球粒子和液体椭球粒子在零阶Bessel波束和一阶Bessel波束照射下,其负声辐射产生的初始角度存在明显的区别,这也说明了粒子操控技术的难易程度。 图2 零阶和一阶Bessel波束轴向入射时刚性椭球轴向声辐射力Fig.2 The axial acoustic radiation force of a rigid spheroid illuminated by the zeroth and first order Bessel beams 图3 细长椭球在一阶Bessel波束入射下的二维散射指向性图Fig.3 The 2D polar plots for a prolate spheroid illuminated by the first order Bessel beam 上文介绍了椭球粒子在Bessel波束轴向入射下,其轴向声辐射力函数的计算公式。根据该计算公式,只需要计算出任意目标物在外界波束的照射下的声散射系数,并且根据该入射波束的波型系数即可准确地计算出该目标物粒子的声辐射力。图4和图5分别给出了刚性介质和液体介质的椭球粒子声辐射力函数计算结果,给出了扁平椭球粒子(a/b=1/2)、标准球粒子(a/b=1)和细长椭球粒子(a/b=2)分别在零阶Bessel波束和一阶Bessel波束轴向入射的情况,其中计算的入射波频率步长δkb=0.1,计算的入射波的波锥角步长是δβ=1◦。为了更好地分辨负声辐射力的分布区域,本文以Yz=−1×10−6为分界过渡线,如图4和图5黑线所示。 从图4观察可知,在零阶Bessel波束和一阶Bessel波束照射下,无论是扁平椭球粒子,或是细长椭球粒子,亦或是标准球粒子,该类粒子都将不会产生负声辐射力的情况,并且随着a/b的增加,轴向声辐射力函数Yz的最大值将逐渐减少。这是因为,根据声辐射力的计算公式可知,其声辐射力函数与对应粒子的外界波束照射下的声散射系数有很大的关系,刚性椭球粒子的散射形态函数与粒子的本身外形尺寸(粒子自身的曲率)存在紧密的关系,在粒子由扁平椭球粒子向细长椭球粒子的变化过程中,粒子的曲率不断降低,因此对应的声散射系数也将不断减小,由此可间接推断出粒子的声辐射力函数也将不断减小。 在一阶Bessel波束的照射下,相对于零阶Bessel波束照射的情况,椭球粒子将产生负声辐射力,负声辐射力与粒子的入射波有很大的关系,因为在前面已经介绍,一阶Bessel波束的中部声压为零,这更加有助于抑制目标物粒子的背向散射,有利于负声辐射力的产生。 扁平椭球粒子产生负轴向声辐射力的大致初始位置是kb=1.8,β=62◦,标准球粒子的大致初始位置是kb=1.7,β=64◦,细长椭球粒子的大致初始位置是kb=1.6,β=68◦。除此之外,从图4观察可知,产生负轴向声辐射力的面积:扁平椭球粒子>标准球粒子>细长椭球粒子,因此可知随着a/b的增加,负轴向声辐射力的面积将逐渐减少。因此可以得到,无论是从产生入射波波锥角的最小值的角度,还是产生负声辐射力的面积对应的频率范围和波锥角的范围的角度,刚性扁平椭球粒子更加有助于产生反向声辐射力。 图5给出了正己烷椭球粒子分别在零阶Bessel波束和一阶Bessel波束轴向入射下的轴向声辐射力函数,其中计算的入射波频率步长δkb=0.1,计算的入射波的波锥角步长是δβ=1◦。对于正己烷,其密度为ρ0=656 kg/m3,声速为c0=1065 m/s。 图4 刚性椭球粒子的轴向声辐射力Fig.4 The axial acoustic radiation force of a rigid spheroid 从图5观察可知,在零阶Bessel波束和一阶Bessel波束的照射下,随着a/b的增加,轴向声辐射力函数Yz的最大值将逐渐增加。这一现象明显不同于刚性椭球粒子,这是因为刚性椭球粒子在外界声波的照射下,只存在镜反射波和Franz波,这两种波只与粒子本身外形尺寸有关。然而,液体椭球粒子相对于刚性粒子还存在反射和折射现象,因此其声辐射力的幅值也将不止受到粒子本身尺寸的影响。 在零阶Bessel波束的照射下,扁平椭球粒子在计算频率范围内产生负向声辐射力的初始位置大概是在kb=5,β=75◦处,标准球粒子的初始位置大概是在kb=3.2,β=41◦处,细长椭球粒子的初始位置大概是kb=2.8,β=31◦。另外,明显观察可知,产生负轴向声辐射力的区域面积:扁平椭球粒子<标准球粒子<细长椭球粒子。因此可以判断,在零阶Bessel波束照射下,细长椭球粒子相对于扁平椭球粒子和标准球粒子更有助于负向声辐射力的产生,并且有利于产生较大的负向声辐射力。 在一阶Bessel波束轴向入射下,扁平椭球粒子在计算频率范围内产生负向声辐射力的初始位置大概是在kb=1.1,β=64◦处,标准球粒子的初始位置大概是在kb=4.1,β=51◦处,细长椭球粒子的初始位置大概是kb=4,β=36◦。另外,明显观察可知,产生负轴向声辐射力的面积:扁平椭球粒子<标准球粒子<细长椭球粒子。因此可以得到,细长椭球粒子能够在较小的波锥角作用下产生负向声辐射力,并且产生负向声辐射力的区域面积比较大。 同时,相对于同一尺寸的正己烷液体椭球粒子,零阶Bessel波束相比于一阶Bessel波束能够在较小的波锥角产生负向声辐射力,并且零阶Bessel波束产生负向声辐射力的区域面积较大。另外,零阶Bessel波束下产生负向声辐射力的幅值更大。因此,对于正己烷液体椭球粒子,零阶Bessel波束应当优先应用在声波操控技术中。 图5 液体椭球粒子的轴向声辐射力Fig.5 The axial acoustic radiation force of a liquid spheroid 光波粒子操控技术的实现和广泛应用,已经充分证明了粒子操控技术的前景和未来,但是由于高强度光波的损伤和光镊子仪器价格昂贵的特点大大限制了粒子操控技术的推广。与之相对应的声波粒子操控技术能够大大弥补光波粒子操控技术的缺点,也必将会拥有更加广泛的应用前景。本文以刚性椭球粒子和液体椭球粒子为对象,研究了椭球粒子在不同的Bessel波束照射下声辐射力的特征。结果表明,对于刚性椭球粒子,扁平椭球粒子相对于细长椭球粒子更有助于激发负声辐射力;对于液体椭球粒子,细长椭球粒子相对于扁平椭球粒子更加容易产生负声辐射力;对于不同介质的椭球粒子,不同的入射波束激发的负声辐射力的效果也存在明显的差异。根据实际应用需要可采用不同介质的粒子和不同种类的Bessel波束。同时需要注意,液体椭球粒子并不一定能完美的保持固定的尺寸,因此可将液体椭球粒子的外表面添加一层极薄的外壳[14],同样也可以达到预想的效果。


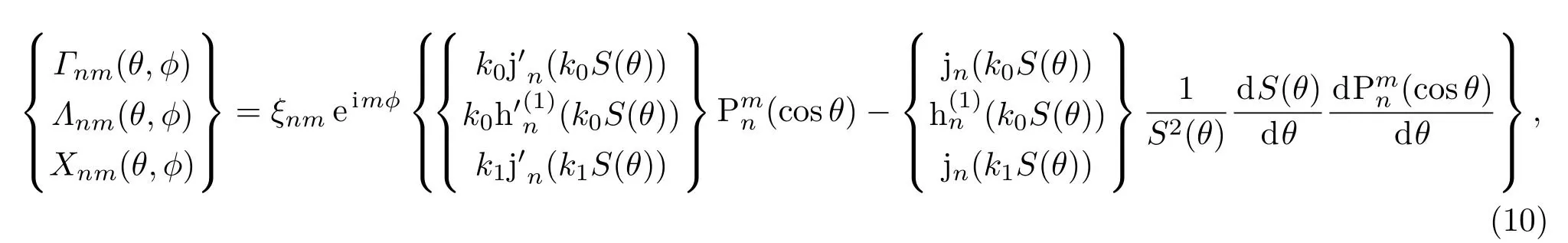
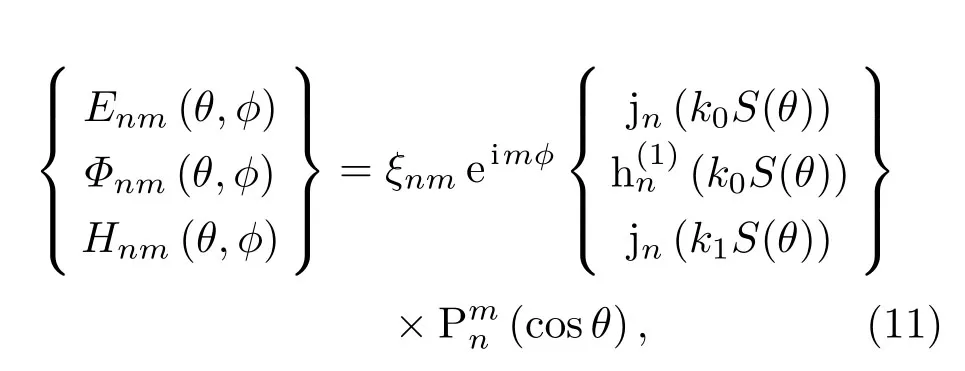





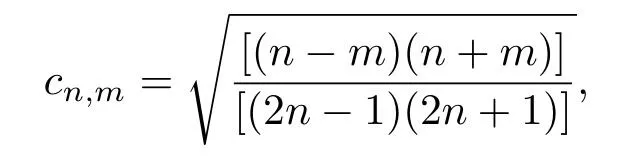
2 理论检验及分析




3 计算结果
3.1 刚性椭球粒子的轴向声辐射力
3.2 液体椭球粒子的轴向声辐射力

4 结论
