一种基于序贯估计的直达声区水面舰船被动测距方法∗

张雪冬 牛海强 吴立新

(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

直达声区水面声源的被动测距一直是研究热点问题，在实际应用中具有重要意义[1−4]。传统的匹配场测距方法通过拷贝场和测量场之间的匹配对距离进行估计，但该方法依赖于对海洋环境参数、尤其是海底参数的准确估计。近年来，基于射线的盲解卷积方法(Ray-based blind deconvolution,RBD)[5−6]被广泛应用。它利用常规宽带波束成形，通过将垂直阵(Vertical line array,VLA)的导向向量指向特定的射线路径(例如直达波)来估计随机声源的相位，进而得到信道响应(Channel impulse response,CIR)。当声源为可控通信声源或船舶噪声时，RBD方法可以只利用接收阵型和阵列位置处的声速剖面(Sound speed profile,SSP)来估计CIR。已有的研究已经证明了利用RBD方法估计CIR的可靠性[7−12]。目前RBD方法被成功应用于声源定位[7−9]、接收阵阵型估计[10−11]和海底参数反演[12−13]中。在利用RBD方法进行被动测距方面，已有的研究主要是通过基于匹配场[7]、基于声线多途时延差[8]和阵列不变量[9]等方法，对RBD估计到的CIR(简称为RBD-CIR)进行处理。但海底参数未知时，匹配场方法和基于声线多途时延差的方法不再适用；在复杂波导中，如声速剖面存在跃层或海底为多层分布时，对阵列不变量的估计也变得复杂。本文利用RBD-CIR的直达波相对参考阵元的到达时间差和声速剖面信息，基于序贯方法，对声源-接收距离进行估计，避免了对海底参数和阵列不变量的估计，并利用2016年美国圣巴巴拉海峡实验数据验证了该方法的有效性。由于受实验环境海深的限制，直达声区仅在<3.5 km的范围内，但此方法仍适用于深海环境的直达声区，测距范围可达几十千米[14−15]。

序贯方法利用状态-空间方程来估计和更新系统的状态值，利用前一状态的估计值和更新值来对下一个状态进行预测，其估计值和更新值由关联了声学测量量与待同化量的声传播模型来得到[16]。常用的序贯方法有卡尔曼滤波[16−17]、集合卡尔曼滤波(Ensemble Kalman filter,EnKF)[18−19]和粒子滤波[17,20]等。这几种方法均在海洋目标跟踪定位方面进行了应用并取得了很好的效果。本文选择了EnKF作为序贯估计滤波器来对声源-接收距离进行估计。EnKF 基于贝叶斯原理[21]，利用集合成员分布来模拟待估计参数，并假设过程中的先验概率分布、似然函数和后验概率分布均服从高斯分布，在非线性系统中有较好的表现。

本文主要分为以下几个部分：首先介绍基于射线的盲解卷积方法和基于状态-空间模型的EnKF方法；第二部分对2016年美国圣巴巴拉海峡实验数据进行处理，并将序贯估计结果与测量值和几何方法的结果进行了比较，并对结果进行了分析；第三部分比较了本文方法和传统匹配场方法的测距结果；最后对本文的工作进行了总结。

1 理论

1.1 RBD方法[5−6]

假设位于海洋信道中点源发射的时域信号为s(t)，其频域表达式为S(ω)=|S(ω)|eiΦs(ω)。则第j(j=1,2,···,N，N为阵元个数)个VLA阵元所接收到的信号可表示为

其中，zs为声源深度，zj为第j个VLA阵元深度，G(zj,zs,ω)是声源和第j个VLA阵元之间的格林函数。对于适用于射线方法的高频信号，各个射线路径的到达角θ可以通过N个阵元的接收信号做常规波束形成得到

其中，到达第j个VLA阵元的第k条射线与到达参考阵元的时延差τj,k可以通过常规波束形成得到，T(θk)与频率几乎无关，主要由声源和VLA之间的射线传播时间决定[22]。RBD方法利用接收信号波束形成B(ω;θk;N)后的相位

来对接收信号的相位进行旋转，从而抵消未知的声源相位谱Φs(ω)，因此有

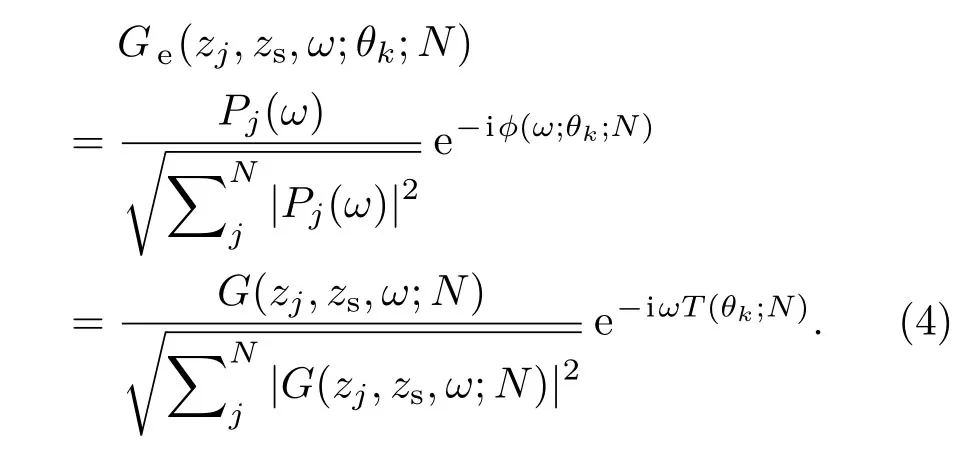
在大多数浅海信道中，信道响应(公式(4))中的分母在频率上足够恒定，所以可以通过平方根项的归一化消除声源信号幅度对估计结果的影响。最后，将RBD-CIR的直达波的相对到达时间差作为测量值，利用EnKF，可对声源-接收距离进行估计。

1.2 EnKF[21]

序贯估计提供了一个状态-空间模型，当出现新的观测值时可对状态值进行预测和更新，它模拟了状态向量与观测向量之间的关系，该模型由状态方程(5a)和测量方程(5b)构成：

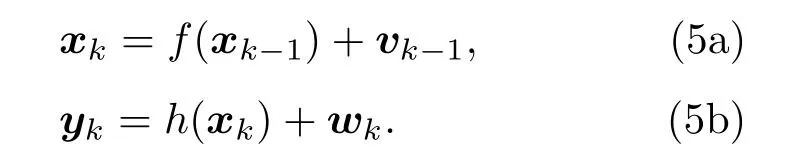
在本文中，状态向量xk为声源深度和声源-接收距离在第k个时间步长时的值。状态方程预测算子f(·)模拟了状态向量随时间步长的变化过程，由于本文不考虑声源的运动模型，所以该算子取为单位矩阵I。状态噪声vk表示了状态方程预测结果和真实结果的误差，通常情况下，认为其服从高斯分布。本文中观测向量yk为直达波在不同接收深度上的相对到达时间差(以中间阵元为参考阵元)，该时间差从RBD-CIR中提取得到。测量算子h(·)代表状态向量xk与观测向量yk之间的关系，在本文中利用射线数值模型Bellhop[23]来得到。测量噪声wk描述了测量值yk与状态方程预测值h(xk)之间的误差。

EnKF 本质上利用采样集合的概率密度分布来描述状态向量xk和测量向量yk，将集合的均值作为估计结果。假设状态向量的初始集合为=1,2,···,M}并服从正态分布，其中i表示集合成员序号，M表示集合成员个数。当vk和wk服从均值为0，方差为Vk和Wk的高斯分布且互不相关时，公式(5a)和公式(5b)可改写为

其中，和表示由状态方程得到的预测状态向量及其协方差矩阵，表示由测量方程更新后得到的状态向量，H是h(·)的线性化算子，K表示Kalman增益，上标T表示矩阵转置。

由于EnKF 用集合中成员的概率分布来表达概率密度函数，则预测状态向量集合在时间步长k的采样均值和协方差矩阵可表示为

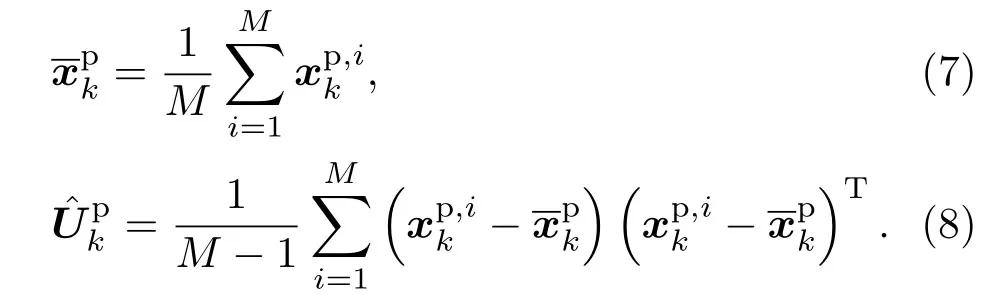
可以看出，当M趋于无穷时，由于收敛于真实的状态向量值，因此趋于真实的误差协方差矩阵。而且状态-空间模型中包含算子H的项都可由以下公式代替

由此可看出，每个由状态方程产生的状态向量成员可以被更新为

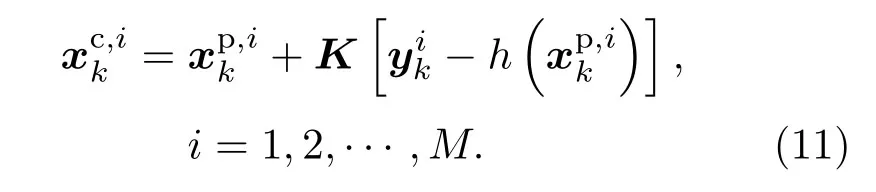
则更新后的状态向量集合会作为初值来递归地产生下一步预测状态向量集合的初值最终的估计结果为状态向量在收敛阶段的后验概率密度(Probably density function,PDF)的平均值。由于EnKF 无需得到状态预测算子f(·)和测量算子h(·)的线性化表达式，在非线性系统中具有很大的优势。

2 实验数据处理结果

为了验证上述方法的有效性，本文基于序贯估计利用RBD-CIR提取的直达波相对到达时间差来估计声源-接收距离，并对实验数据结果进行了分析。实验数据来自于2016年9月美国圣巴巴拉海峡实验(SBCEx-16)，实验区域为以圣巴巴拉海峡为中心、由34.3◦N、120.2◦W和34.2◦N、120.0◦W圈出的方形区域，如图1(a)所示。该区域位于圣罗莎岛北部、加利福尼亚海岸线17 km以外，南北长约11 km、东西长约18 km。实验区域的海深从西北部(500 m)向东南部逐渐增加(590 m)，而本文所研究的区域位于东南部分，如图1(b)所示。图1(b)中虚线为航道边界，航道宽1 n mile，航道间的间隔也为1 n mile。4个32元的VLA 均匀锚系在航道中心线处的海底。本文仅对其中一个VLA(图1(b)红点)的接收信号进行了分析。该VLA锚系在深580 m的海底上方约5.8 m处，由两个子阵构成，上方的子阵由16个间隔1 m的阵元构成，其中第一个阵元在实验期间没有收集数据；下方的子阵由16个间隔3.75 m的阵元构成；两个子阵之间间隔5.6 m，总有效阵长为75.85 m。接收信号采集系统的采样频率为25 kHz。实验中温盐深仪(Conductivity,temperature,depth,CTD)测量到的16个剖面的平均声速剖面见图1(d)。可以看出，声速在水面附近为1510 m/s，在海深50 m附近迅速降为1491 m/s，并逐渐过渡到海底580 m处的1485 m/s，因此声速剖面在50 m以上存在跃层。

图1(b)中的蓝色圆点表示商船Anna Maersk在9月16日12:14:30–12:19:30期间每间隔10 s的航迹，由自动测量系统(Automatic identification system,AIS)测得，图中蓝色箭头表示船行进方向。在此期间，Anna Maersk 距离VLA最远的位置(点P)有3440 m，而最近有1634 m。受航道条件的限制，实验过程中不存在距离VLA 小于1.6 km的航船；受该区域海深的限制，当声源-接收距离大于3.5 km时，航船超出了直达声区的范围。所以仅对有限距离范围内的航船噪声进行处理。图1(c)为图1(b)中绿色圆点所示航迹的海底回声定位图像。可以看出，该环境下海底呈现出多层分布，且海深随距离的变化而变化。

以声源-接收距离r=3440 m为例(即图1(b)中的点P)，图2介绍了利用RBD方法估计CIR的详细步骤。图2(a)为VLA上第一个阵元(498.35 m)处接收到的5 s 长的舰船辐射噪声信号。对VLA所有阵元的接收信号做常规宽带波束形成，处理频带为150∼1000 Hz，信号时间长度为5 s，得到波束图如图2(b)所示，其中直达波和海底反射波的到达角分别为θD=−10◦和θB=12◦(以水平到达方向为0◦，垂直到达方向为90◦)。对VLA所有阵元的接收信号在直达波到达方向θD上做波束形成(公式(2))，将波束形成后的信号与接收信号做匹配滤波，然后对幅度进行归一化(公式(3)∼(4))，得到RBD-CIR如图2(c)所示。从图中可以观察到直达波和两组到达角相同的海底反射波，这也印证了海底多层分布的情况。

图1 2016年美国圣巴巴拉海峡实验Fig.1 2016 Santa Barbara Channel Experiment

图2 利用RBD方法估计信道响应的实现步骤Fig.2 The steps for estimating CIR using RBD method

对图1(b)中Anna Maersk的航迹上所有接收信号均做常规宽带波束形成，所得结果随距离的变化如图3所示，其中分别用蓝色和红色加号标出了直达波θD和海底反射波θB的到达角。从图3中可以看出清晰的直达波，并且随着距离增加而逐渐向0◦(水平方向)靠近。利用所有声源-接收距离r上的直达波到达角θD的波束形成结果估计其对应的RBD-CIR，并提取其直达波在深度zj(第j个VLA阵元)上的到达时间TD(zj)，来计算其相对于参考阵元的到达时间差δT，其中参考阵元为第16个阵元，即δT(zj)=TD(zj)−TD(z16)。所得直达波相对到达时间差结果如图4中黑色加号所示。为了便于比较，图4中对每个距离上的时间差相对于上一个距离的结果整体向右平移了5 ms，从左至右的距离逐渐增加。可以观察到，直达波的相对到达时间差δT随距离的变化而变化，所以利用该提取量对距离进行估计是可行的。

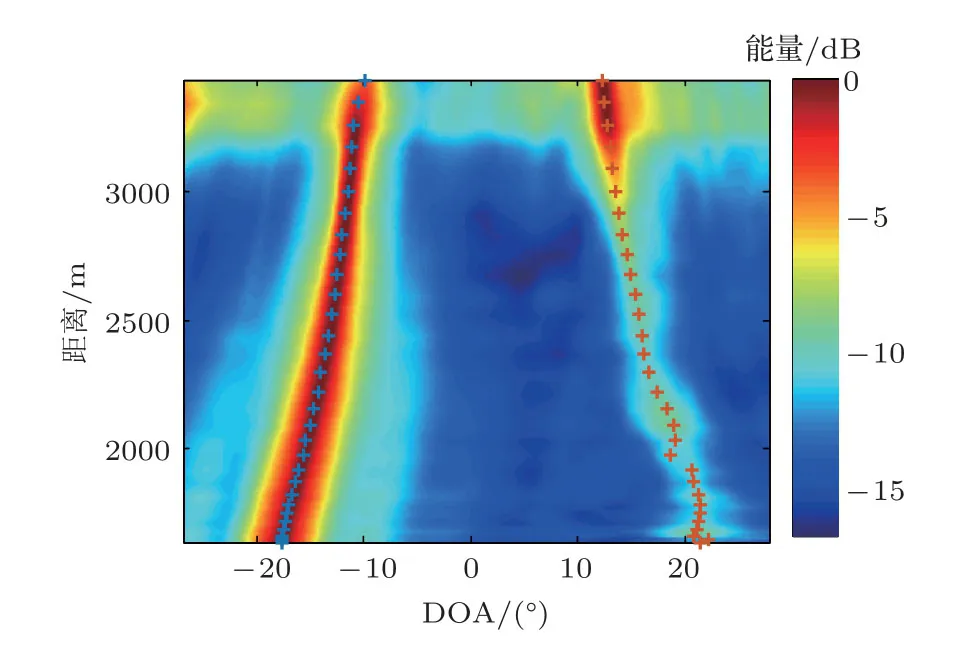
图3 接收信号常规宽带波束形成图Fig.3 Evolution of the beamformed receiving signals obtained from plane-wave beamforming

利用图4中的直达波相对到达时间差δT对声源-接收距离r进行估计。由于声源深度zs也会对δT产生影响，所以这里分析δT对zs和r的敏感性。由于已知声源为水面舰船，所以仅对zs=1∼20 m的情况进行讨论。利用Bellhop计算zs=5 m、r=3440 m(仿真图1(b)中点P的情况)时的δT，以及zs和r分别在1∼20 m和3000∼4000 m的范围内变化时的二者的差值在深度上的平均值(即公式(12))随zs和r的变化分别如图5(a)和图5(b)所示，仿真时所使用的声速剖面如图1(d)所示。

图4 不同距离上，由RBD-CIR提取的和利用EnKF 估计结果得到的直达波的相对到达时间差Fig.4 The direct ray-path arrival time differences extracted from RBD-CIRs and calculated by the EnKF estimation results,respectively,for different source-receiver distances

图5 敏感性分析Fig.5 Sensitivity analysis

可以看出，相比于声源-接收距离r，声源深度zs的变化对δT的影响较小。所以在对r进行估计时，虽然也将对zs的估计包含在内，但由于δT对zs在1∼20 m范围内的变化不敏感，所以zs的估计值并不能作为最后的估计结果，而是为了对r的估计增加一定的宽限，所以本文并未对声源深度的估计结果进行详细研究。

将图4中黑色加号所示的直达波相对到达时间差δT作为观测值，利用M=20个集合成员的EnKF 滤波器对声源深度zs和声源-接收距离r进行追踪，即xk=[zsr]T。所使用的初值、状态方程的协方差和搜索区间如表1所示，并令状态向量协方差的初值等于根据状态向量的特性，将其协方差设为由于距离r的变化比较大，所以这里针对距离设定了较大的协方差参数。测量方程噪声协方差取0.05 ms。由于zs对直达波相对到达时间差的影响不大，不妨设其初值为10 m，区间为1∼20 m。对声源-接收距离r的初值分别为1000 m、1600 m和3000 m的情况进行了讨论。通常情况下，序贯方法不需要设定搜索区间，但为了使反演结果更符合海洋环境参数的一般设定，这里对状态向量限定了上下限。但从图6中声源-接收距离的后验PDF 在不同时间步长上的结果中看出，由于PDF 并未碰到搜索区间的上下限，所以上下限的设定对反演结果的影响很小。为了使每个距离的估计结果更加稳定，在每个距离点上均进行了10个时间步长的迭代，则对31个距离点估计的总时间步长为310。因此在每个距离点上需要计算200个点的直达波相对到达时间差。在10个时间步长以后，不同初值的测距估计结果非常接近。在10个时间步长之前，当r0=1600 m时(图6(b))，由于其接近第一个测距点的测量值1640 m，其后验PDF 快速收敛到测量值附近；而当r0=1000 m和3000 m时(图6(a)和图6(c))，二者后验PDF 在10个步长后收敛到测量值附近。随后，声源-接收距离r的后验PDF在每个距离点上(10个步长范围内)均可以较快地过渡到收敛阶段，并趋于稳定。

表1 序贯估计的初值及滤波器参数Table1 Initial settings of the sequential parameter estimation

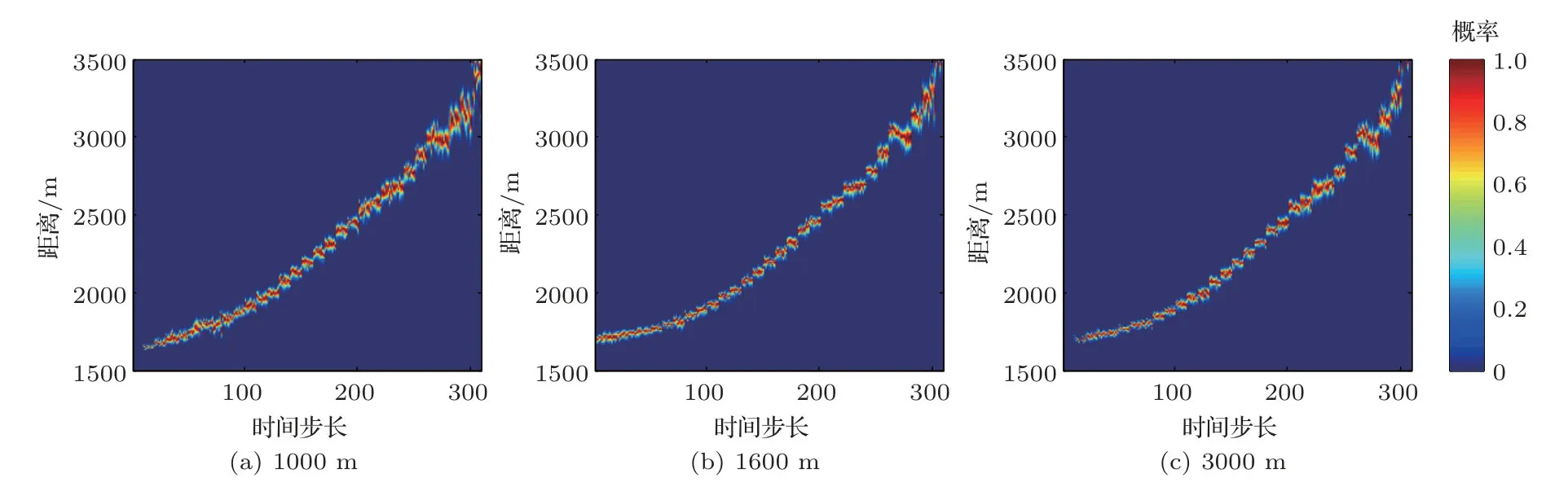
图6 声源-接收距离初值不同时，声源-接收距离的后验PDF 随时间步长的变化结果Fig.6 The estimated results of source-receiver distances as evolving marginal posterior PDFs with different initial values of the source-receiver distances

当声源-接收距离初值r0为1600 m时，将声源深度zs和距离r的后验PDF(图6(b))在每个距离点上最后一个步长的均值作为最终的估计结果，利用Bellhop[23]和图1(d)中的声速剖面模拟直达波的相对到达时间差δT，如图4中红色虚线所示。为了便于比较，采取了与RBD-CIR提取到的δT同样的操作，即对每个距离上的时间差相对于上一个距离的结果整体向右平移了5 ms。可以看出二者符合得很好。图7(a)中红色叉号虚线表示r0=1600 m时，利用EnKF所得的最终测距结果，并将其与AIS系统测量的结果(蓝色圆圈)以及几何方法的计算结果(rG，灰色实线)进行比较。几何方法是将信道视为理想波导(海水声速为常数)，并将声源深度视为0 m，通过直达波的到达角和接收阵所有阵元的深度，来估计声源-接收距离，即rG(zj)=−zj/tan(θD),(j=1,2,···,N)。由于VLA 具有一定的长度，所以使用不同的阵元深度会得到不同结果的rG。图7(b)中比较了当r0=1600 m时，EnKF测距结果(红色叉号)和几何方法结果rG(灰色实线)与AIS 测量值的误差绝对值|δr|。EnKF的测距结果的误差范围为1∼186 m，每个距离上的误差小于6%。由于无法确定接收器深度，rG的误差随着所使用的接收器深度zj的变化而变化，误差最大可达675.6 m。若使用所有深度的平均值(526.37 m)作为接收深度，即tan(θD)，此时的最大误差530.1 m，相对误差可达16%。

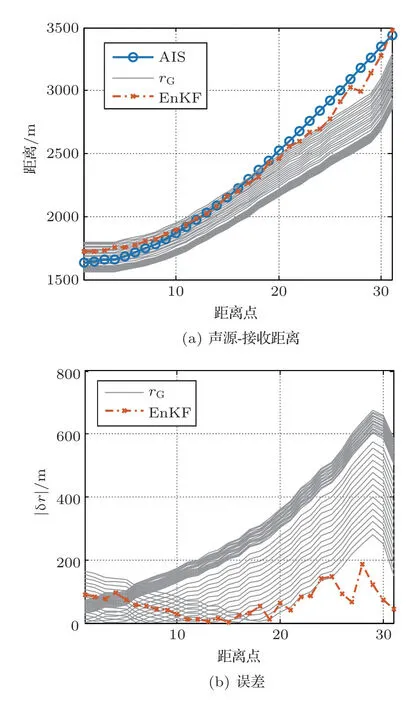
图7 不同方法估计得到的声源-接收距离及其与AIS 测量值的误差Fig.7 The source-receiver distances obtained with different methods and the source-receiver distance differences between the estimations with different methods and the AIS measurements

比较不同距离上几何方法估计的距离rG与AIS结果的误差，可以发现随着距离的增加，误差也随之增大。这是由于声速剖面存在跃层，见图1(d)。图8是当声源-接收距离r分别为1634 m(实线)和3440 m(虚线)时利用Bellhop模型仿真得到的在VLA 平均深度上(526.37 m)的直达波(D，由蓝线表示)和海面反射波(S，由红线表示)的路径图。声源深度假设为10 m，所使用的声速剖面如图1(d)所示。从图8可看出，当声源-接收距离r=1634 m时，直达波和海面反射波经过跃层的长度较短，受其影响较小，直达波仍可视为声源和接收器之间的直线，所以几何方法估计的距离较为准确；但当声源-接收距离r=3440 m时，直达波和海面反射波经过跃层的长度大大增加，根据Snell定律[22]，射线在此区域会发生较大弯曲，所以无法将直达波路径视为声源与接收器之间的直线，几何方法估计结果的误差大大增加。

图8 声源-接收距离不同时，利用Bellhop 仿真计算得到的直达波(D)和海面反射波(S)的路径图Fig.8 The direct(D)and the surface-bounced(S)ray-paths simulated by Bellhop with different source-receiver distances

3 与传统匹配场方法比较

将本文方法的结果与传统匹配场方法作比较。匹配场方法[24]利用代价函数在参数空间内进行搜索来估计声源-接收距离r和声源深度zs，这里代价函数表示为[24]

其中，F表示频点数，本文在160∼480 Hz中均匀选取了12个频点；BMF是在频率为fk时的Bartlett匹配滤波结果，并且有

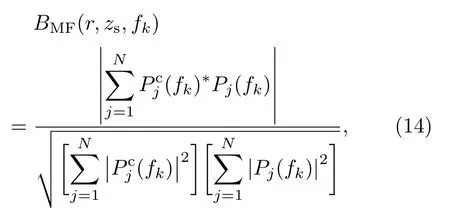
其中，为第j个阵元的接收信号在fk时的复声压，*表示复转置，为理论声压，在这里为利用Kraken声场模型[25]根据图9所示海洋环境模型所得声压。由海底回声定位仪所测图像(图1(c))以及盲解卷积所得信道响应(图2(c))可知，该区域海底情况较为复杂，且海底深度也在不断变化。但为了简化模型，这里将其假设为两层分布的水平不变模型，上层为软沉积层，下层为半无限大的硬基底。沉积层厚度为d，沉积层声速cs和基底声速cb、沉积层吸收系数αs和基底层吸收系数αb都假设为不随深度变化。而沉积层密度ρs和基底密度ρb可以根据Hamilton 经验公式(公式(15))由沉积层声速cs和基底声速cb计算得到(文献[26]中也曾做过类似处理)

图9 海洋环境模型Fig.9 The range-independent environment model

利用图9中的海洋环境模型对r和zs进行估计，并且其搜索区间分别为900∼4000 m和1∼20 m，步长分别为10 m和1 m，因此在每个距离点上需要计算311个距离、20个声源深度和12个频点处的声压。由于该区域海底参数未知，所以根据已有的经验对海底参数进行多种假设，其具体情况如表2所示。最后所估计得到的声源-接收距离r如图10(a)所示，其与AIS 测量值的误差绝对值|δr|如图10(b)所示。由图可知，在海底参数取组合1和4时，r的匹配场估计结果在所有距离点上与测量值AIS 符合得较好，此时最大相对误差分别为12%和9%，仍大于本文方法的误差6%。若改变沉积层厚度以及其他海底参数(组合2和3)，此时r的估计结果在某些距离点上(例如第29、30个距离点)最大相对误差均可达到70%；若排除这些点，r的最大相对误差分别为12%和7%，仍大于本文方法的结果。由此可看出，海底参数的选取对匹配场方法的测距结果影响很大。

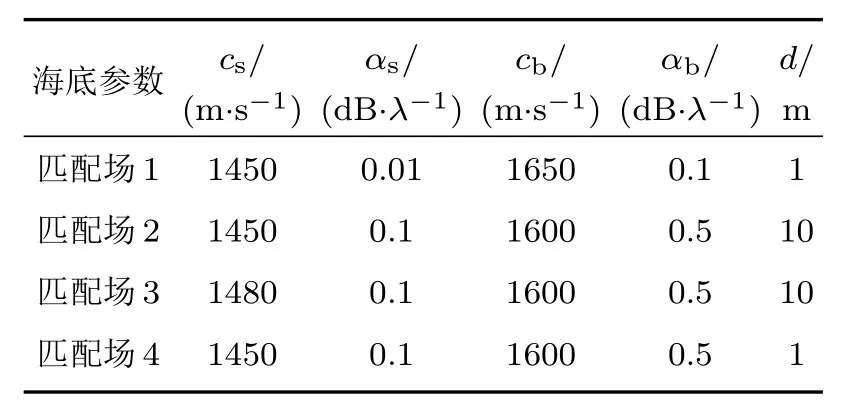
表2 匹配场方法所使用的海底参数组合Table2 Geoacoustic parameters for matched-field method

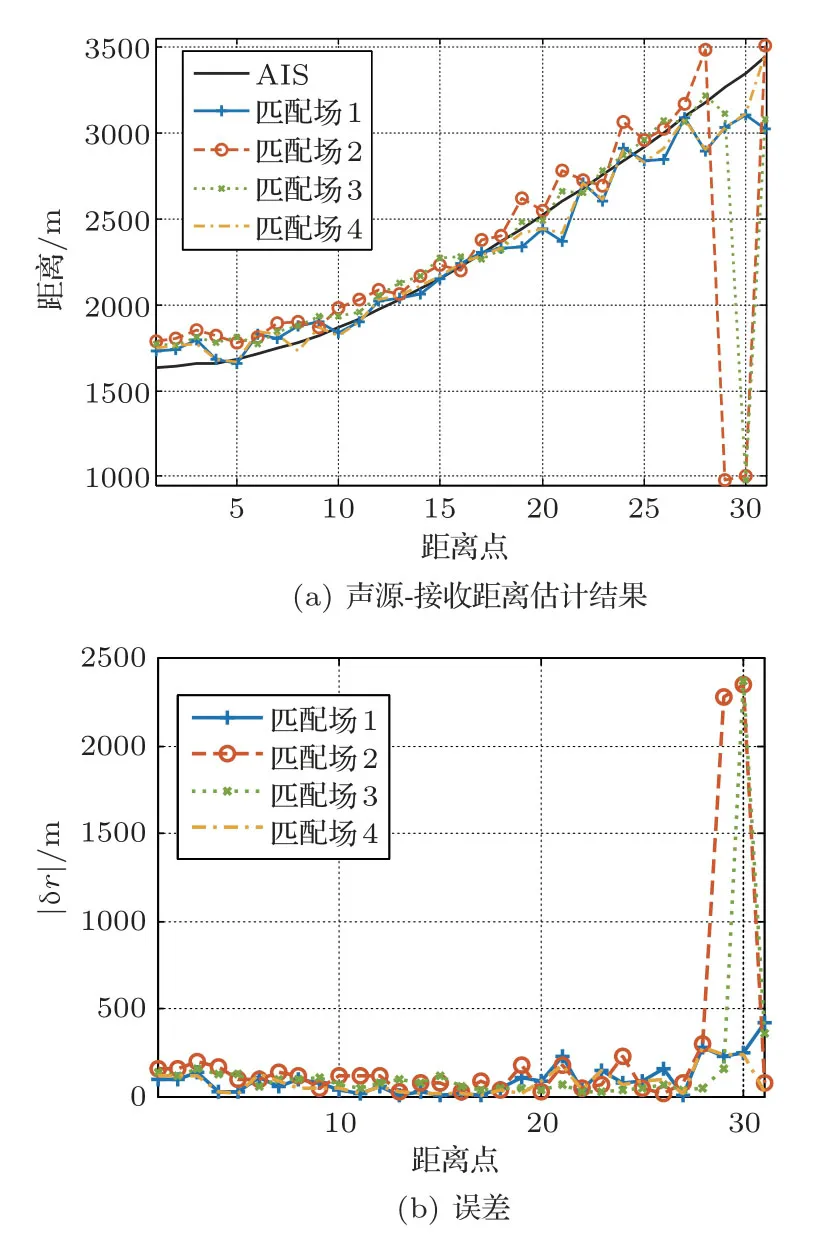
图10 不同方法得到的声源-接收距离估计结果及其与AIS 测量值的误差Fig.10 The source-receiver distances estimated by different methods and the source-receiver distance differences between the estimations and the AIS measurements

4 结论

本文对2016年美国圣巴巴拉海峡实验数据进行了处理，通过垂直阵在1.6∼3.5 km 直达声区范围内接收到的水面舰船辐射噪声数据，利用RBD方法来估计船和接收阵之间的信道响应，提取直达波在垂直阵不同阵元上的相对到达时间差，基于序贯方法对声源-接收距离进行了估计，并将距离的估计结果与测量值、几何方法和传统匹配场方法的结果进行了比较。由于不需要对海底参数和阵列不变量进行估计，该方法在声速剖面存在跃层和海底多层分布的复杂海洋环境下仍然适用，要优于传统匹配场方法。本文方法距离估计值与测量值的相对误差在6%以内，并且小于几何方法的误差。若根据已有经验对海底参数进行假设，本文方法距离估计值与测量值的相对误差仍小于传统匹配场方法。由本文方法得到的估计值所仿真的直达波相对到达时间差与测量值吻合得很好。由于受到实验条件的限制，直达声区的范围较小，下一步将对深海环境下该方法的有效性进一步进行验证。

致谢由衷感谢佐治亚理工学院Karim G.Sabra教授提供的2016年美国圣巴巴拉海峡实验数据，感谢参加海上实验的全体工作人员，他们的辛勤劳动为本文提供了宝贵的实验数据。