利用频域β-warping变换的浅海目标航向估计方法∗

董 阁 郭良浩 徐 鹏 闫 超

(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

纯方位目标运动分析方法仅利用目标方位信息估计目标的距离、速度和航向等运动状态参数信息[1−2]。但根据纯方位目标运动分析的可观测性理论[3]，若观测平台未进行有效机动，目标运动状态信息具有不完全可测性。当目标进行匀速直线运动时，对于单一静止的观测平台，仅目标航向信息是可观测的。在实际应用中，针对单一静止的观测平台，如何获取目标航向信息对目标的探测和识别具有重要的意义。

针对匀速直线运动目标，部分学者[4−6]利用目标方位与目标航向的几何关系估计目标航向。根据目标航向的数学模型，张晓勇等[4]提出了最小二乘目标航向估计方法。孙少杰等[5]采用伪线性方法对目标航向的数学模型进行处理，提出了伪线性最小二乘目标航向估计方法。陈喆等[6]首先利用线性回归理论分析了数据样本的线性相关性，而后利用最小二乘方法进行航向估计。仅利用目标方位的目标航向估计方法收敛时间较长，航向估计精度较低。

考虑到海洋信道对声传播的影响，将信号处理方法与水声传播规律相结合，可以有效地提高声呐设备的探测性能。在浅海水平不变远场条件下，如何利用低频声场的声强在距离-频率平面上形成的干涉条纹提取目标运动状态信息成为一个重要的研究方向。当目标的运动轨迹相对于与观测平台存在最近通过距离时，余赟等[7]首先对干涉条纹进行Hough 变换，估计波导不变量和目标最近通过距离与目标速度的比值，而后估计目标航向。当目标的运动轨迹相对于观测平台不存在最近通过距离时，王炳辉等[8]直接建立了目标航向、波导不变量和干涉条纹的关系模型，提出了利用Hough 变换对目标航向和波导不变量进行联合估计的方法。同样，针对无目标最近通过距离的情况，在浅海Pekeris波导条件下，余赟等[9]首先利用Radon变换提取干涉条纹，假定波导不变量值为1，采用二次测量法对目标进行估计。

相比于仅利用目标方位的航向估计的方法，利用浅海低频声场干涉条纹提取目标航向信息的方法有效地提高了目标航向的估计精度，但要求LOFAR谱中具有明显的干涉条纹，且具有较高的信噪比。同时，以上方法均假定目标是匀速直线运动的，但在实际应用中，在观测时间范围内，很难保证目标持续进行匀速直线运动。因此，在目标进行变速直线运动时，结合浅海低频声场的声场特征，如何快速有效地估计目标航向具有重要的研究价值。

近年来，大量国内外学者致力于利用warping变换从简正波互相关项中提取与目标距离相关的信息，再进行目标运动状态参数的估计。根据简正波水平波数差与波导不变量的关系，戚聿波等[10]提出了一种基于频域β-warping变换算子的被动测距方法。在之前的研究中，将当前时刻与初始时刻目标距离的比值定义为距离特征量，针对已有的利用LOFAR谱图估计距离特征量的方法[11−12]估计精度不够的问题，提出了利用频域β-warping变换的距离特征量估计方法[13]，得到了修正纯方位扩展卡尔曼滤波方法。但频域β-warping变换需要已知波导不变量的值，在实际应用中，很难获取波导不变量的真实值。郭良浩等[14−15]选取特定的频域β-warping变换算子的系数，研究表明，当波导不变量的估计值为真实值的q倍时，若q、信号带宽和频域β-warping变换算子的系数之间满足一定的关系，则简正波互相关项通过频域β-warping后的脉冲时延也为波导不变量取真实值时的q倍。

针对已有目标航向估计方法需要目标进行匀速直线运动的问题，本文将通过频域β-warping变换得到的距离特征量信息引入到纯方位目标航向估计方法中，提出了一种利用频域β-warping变换的目标航向估计方法。该方法无需目标保持匀速直线运动，首先利用频域β-warping变换估计距离特征量，而后根据目标方位和距离特征量利用渐近无偏最小二乘方法估计目标航向。考虑到波导不变量的估计误差对频域β-warping的影响，本文选用文献[14]提出的频域β-warping 算子的系数进行频域β-warping变换。数值仿真结果表明，在浅海Pekeris波导环境下，当目标进行匀速直线运动时，相比于常规纯方位目标航向估计方法，本文方法的收敛时间明显缩短，航向估计精度更高。当目标进行变速直线运动时，该方法依然具有较好的航向估计性能。另外，该方法航向估计性能与观测时间内的平均方位变化率密切相关。最后，利用一次实际海试数据验证了本文方法的有效性。

1 利用频域β-warping变换估计距离特征量

在浅海水平不变波导远场条件下，接收信号自相关函数中的简正波互相关的部分可以表示为

其中，S(f)为声源幅度，An(f)为第n阶简正波的幅度，r为接收点和声源的相对距离，γnm为仅与简正波号数有关的常数，β为波导不变量的真实值。假设接收信号的有效频带为[f1,f2]，频域βwarping 变换算子为C为常数。当β1 时，C取内的任意值均可保证频域β-warping 变换重采样后的频带包含接收信号的有效频带范围[10]。假定波导不变量的估计值为且则其中对式(1)进行频域β-warping变换可得

若所选参数满足以下条件[15]：

式(2)可近似为

根据式(4)可以看出，第n阶和第m阶简正波互相关项通过频域β-warping变换得到的脉冲时延为

k时刻的距离特征量定义为k时刻的目标距离与初始时刻的目标距离的比值，即

对初始时刻和k时刻的接收信号自相关函数分别进行频域β-warping变换，可得

将式(7)和式(8)代入式(6)可得

在实际应用中，如果可以获得粗略的水体声速剖面信息，使得波导不变量的估计值在合理的范围内，可以保证式(3)的条件成立，则第n阶和第m阶简正波互相关项通过频域β-warping后的脉冲时延为波导不变量取真实值时的q倍[15]。由式(9)可以看到，k时刻的距离特征量可以表示为k时刻和初始时刻的第n阶和第m阶简正波互相关项对应的脉冲时延的比值。因此，波导不变量的估计误差不会影响距离特征量的估计精度。

2 目标航向估计方法

2.1 渐近无偏最小二乘方法

目标与观测平台在x-y二维平面上的运动态势示意图如图1所示。假定观测平台静止且位于坐标原点，目标做直航运动，目标航向为ϕ，k时刻的目标方位和距离特征量分别为θk和Mk。根据距离特征量的定义和正弦定理可得

根据几何关系可以得到

将式(11)和式(12)代入式(10)得

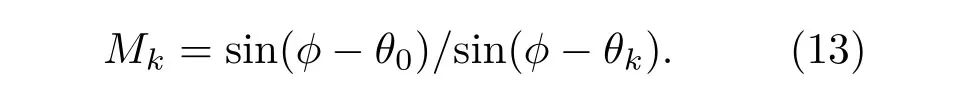
图1 目标与观测平台运动态势示意图Fig.1 The motion state of target and observer platform

假定k时刻的目标方位的真值和估计值分别为和距离特征量的真值和估计值分别为和将目标方位和距离特征量的真值代入式(13)，进一步整理得

其中，X=tanϕ。定义增广状态向量γ=[X,1]T，将目标方位和距离特征量的估计值代入式(14)可得

因为εθ,k足够小，所以cosεθ,k ≈1，sinεθ,k ≈εθ,k，则式(16)化简为

根据式(17)可以得到，均方误差为

假设观测总时长为K+1，则总的均方误差为

其中，

令

可得

其中，

为了得到γ的无偏估计，将γTW γ限定为一个常数同时使达到最小[16−17]。上述问题可以转化为如下条件极值问题：

针对此条件极值问题，可通过拉格朗日乘数法求解,可得[17]

对γ求偏导，并令偏导值为0，得到

根据式(23)可以看到，此问题为广义特征值问题，λ为相对于W的特征值，γ为属于λ的特征向量，最小特征值所对应的特征向量即为该条件极值的解，进而得到目标航向正切值的估计值为

2.2 航向判别方法

目标航向范围为[0,2π]，但反正切函数在[0,2π]内具有多值性，所以获得目标航向正切值的估计值后，需要进行航向判别。图2为目标航向判别示意图，下面以目标初始时刻位于第一象限为例，进行航向判别。

图2 目标航向判别示意图Fig.2 Target course discrimination

当目标沿图2中的虚线运动时，即目标方位不随时间变化，此时可通过判断目标与观测平台的相对距离的变化来估计目标航向。当目标径向远离观测平台时，=θ0；当目标径向接近观测平台时，=θ0+π。

除目标沿图2中的虚线运动的情形外，其余情形可通过目标方位随时间的变化判断目标航向的范围。根据初始时刻的目标方位，将目标航向范围划分为两部分。当目标由初始位置向第I 部分运动时，目标方位范围为[0,θ0)∪(θ0+π,2π]，在[0,θ0)和(θ0+π,2π]范围内，目标方位逐渐减小，航向范围为[0,θ0)∪(θ0+π,2π]。当目标由初始位置向第II部分运动时，目标方位范围为(θ0,θ0+π)，目标方位逐渐增大，航向范围为(θ0,θ0+π)。

根据以上的航向判别的划分方法，若目标初始时刻位于第二象限，当目标方位逐渐减小时，航向范围为[0,θ0)∪(θ0+π,2π]；当目标方位逐渐增大时，航向范围为(θ0,θ0+π)。若目标初始时刻位于第三或第四象限，当目标方位逐渐减小时，航向范围为(θ0−π,θ0)；当目标方位逐渐增大时，航向范围为[0,θ0−π)∪(θ0,2π]。

2.3 性能评价指标

(1)收敛时间

则Kc为航向估计的收敛时间，是用来衡量航向估计方法的解算时间。

(2)均方根误差

本文利用均方根误差(Root mean square error,RMSE)来衡量目标航向的估计精度，k时刻的航向估计的均方根误差定义为

3 仿真研究

采用Pekeris波导模型，海水深度为45 m，海水声速为1505 m/s，海水密度为1.0 g/cm3；海底声速为1596 m/s，海底密度为1.6 g/cm3，海底衰减系数为0.12 dB/λ。观测平台为位于水下20 m的64元水平均匀直线阵，阵元间距为0.5 m。水面目标为单位强度的点源，深度为3 m。信号频率为100∼500 Hz，采样频率为4000 Hz，单阵元接收信号的工作带宽内信噪比为−15 dB。观测平台静止于坐标原点，目标做匀速直线运动，速度为5 m/s，航向为180◦，初始距离为10 km，初始方位为60◦。目标进行匀速直线运动时的目标与观测平台的运动态势如图3所示。观测时间为20 min，以1.024 s作为一帧进行数据处理。

图3 目标进行匀速直线运动时的目标与观测平台的运动态势Fig.3 The motion state of target and observer platform for the target with uniform linear motion

图4 目标进行匀速直线运动时的目标航向估计结果Fig.4 Course estimation results for the target with uniform linear motion

图4(a)为最小方差无失真响应波束形成方法得到的目标方位历程。图4(b)为频域β-warping变换后的时域序列，波导不变量取为1，处理频段为200∼400 Hz。通过提取的不同时刻的脉冲序列时延，估计距离特征量，结果如图4(c)所示。本文利用文献[13]提出的距离特征量平均估计误差来衡量距离特征量的估计精度。距离特征量的平均估计误差定义为

频域β-warping变换方法得到的距离特征量平均估计误差为1.21%。本文将文献[5]中提出的纯方位最小二乘目标航向估计方法作为对比，分析本文提出的利用目标方位和距离特征量的渐进无偏最小二乘目标航向估计方法的性能。根据以上估计的目标方位和距离特征量，分别利用文献[5]和本文方法对目标航向进行估计，结果如图4(d)所示。文献[5]和本文方法的收敛时间分别为13.1 min和4.2 min，第20 min，文献[5]和本文方法的航向估计误差分别为2.57◦和2.30◦。

以上仿真为目标进行匀速直线运动的情形，下面分析本文方法在目标进行变速直线运动的条件下的性能。目标初始速度为5 m/s，初始距离为10 km，初始方位为60◦，航向为180◦。目标先进行匀速直线运动，持续时间为5 min，然后进行匀加速直线运动，加速度为0.01 m/s2，持续时间为10 min，之后继续进行匀速直线运。其余仿真条件与目标进行匀速直线运动时的仿真条件一致。目标进行变速直线运动时的目标与观测平台的运动态势如图5所示。图6为观测时间范围内的目标速度。

图5 目标进行变速直线运动时的目标与观测平台的运动态势Fig.5 The motion state of target and observer platform for the target with variable velocity linear motion

图6 目标速度Fig.6 Target velocity

图7(a)和图7(b)分别为目标方位历程图和频域β-warping变换后的时域序列，图7(c)为目标距离特征量的估计结果，距离特征量的平均估计误差为1.11%。目标航向估计结果如图7(d)所示，本文方法的收敛时间为4.2 min，第20 min，本文方法的航向估计误差为1.30◦。由于文献[5]的方法要求目标进行匀速直线运动，所以针对目标进行变速直线运动的情形，文献[5]的方法无法正确估计目标航向。而本文方法由于引入了距离特征量信息，无需目标保持匀速直线运动，在目标进行变速直线运动时，依然具有较好的航向估计性能。

下面分析两种方法在不同观测误差条件下的估计性能。目标与观测平台的运动态势与目标进行匀速直线运动时的仿真条件相同，目标方位和距离特征量的观测误差均服从零均值的高斯分布，蒙特卡洛仿真的次数为100次。在不同观测误差条件下，两种方法的性能如表1所示。根据表1可以看出，当距离特征量估计误差一定时，随着方位估计误差的增大，两种方法的收敛时间逐渐增大，航向估计精度逐渐降低，但相比于文献[5]的方法，本文方法的收敛时间更短，估计精度更高。当方位估计误差一定时，随着距离特征量估计误差的增大，本文方法的收敛时间逐渐增大，航向估计精度逐渐降低。本文方法由于引入了距离特征量信息，获得了更好的航向估计性能，但当距离特征量误差较大时，本文方法的性能下降，收敛时间大于文献[5]的方法，且估计精度更低。

图7 目标进行变速直线运动时的目标航向估计结果Fig.7 Course estimation results for the target with variable velocity linear motion

表1 在不同观测误差条件下的两种方法性能Table1 The estimation performance of the method with different observation error

下面分别研究两种方法在不同目标航向、不同初始距离和不同目标速度条件下的方法性能，其余仿真条件与目标进行匀速直线运动时的仿真条件相同。目标方位和距离特征量的观测误差均服从零均值的高斯分布，方位估计误差标准差σθ=0.5◦，距离特征量估计误差标准差σm=0.05，蒙特卡洛仿真的次数为100次。定义θr为观测时间范围内的平均方位变化率，即

其中，T为采样时间间隔。在不同目标航向条件下，两种方法的航向估计均方根误差如图8所示，可以看到，本文方法相比于文献[5]方法的收敛时间更短，航向估计均方根误差更小。在不同目标航向条件下，观测时间内的平均方位变化率如图9所示，可以看到，除目标航向为60◦和240◦两种情形外，当目标航向接近60◦或240◦时，平均方位变化率较小，对应的航向均方根误差较大。当目标平均方位变化率较大时，对应的航向均方根误差较小。当目标航向为60◦或240◦时，即目标沿图2中的虚线进行运动，则观测时间内的目标方位与不随时间变化，目标平均方位变化率为0，此时根据航向判别方法即可确定目标航向，无需利用目标方位和距离特征量进行估计，因此，在平均方位变化率为0时，依然具有较好的航向估计性能。通过以上分析可以看到，两种方法的航向估计性能与观测时间内的平均方位变化率密切相关。不同初始距离条件下，两种方法的航向估计均方根误差如图10所示，观测时间内的平均方位变化率如图11所示。平均方位变化率是随着初始距离的增大而逐渐减小，两种方法的航向估计均方根误差随着初始距离的增大而逐渐增大。不同目标速度条件下，两种方法的航向估计均方根误差如图12所示，观测时间内的平均方位变化率如图13所示。平均方位变化率是随着目标速度的增大而逐渐增大，两种方法的航向估计均方根误差随着目标速度的增大而减小。因此，根据不同初始距离条件和不同目标速度条件下的航向估计均方根误差与平均方位变化率的结果，同样可以得到，两种方法的航向估计性能与观测时间内的平均方位变化率密切相关，当平均方位变化率较大时，可以获得较好的航向估计性能。

图8 不同目标航向条件下的航向估计均方根误差Fig.8 The RMSE of course estimation with different target course

图9 不同目标航向条件下的平均方位变化率Fig.9 The average bearing rate with different target course

图10 不同初始距离条件下的航向估计均方根误差Fig.10 The RMSE of course estimation with different initial target range

图11 不同初始距离条件下的平均方位变化率Fig.11 The average bearing rate with different initial target range

图12 不同目标速度条件下的航向估计均方根误差Fig.12 The RMSE of course estimation with different target velocity

图13 不同目标速度条件下的平均方位变化率Fig.13 The average bearing rate with different target velocity

4 实验研究

下面利用一次实际海试数据对本文方法进行验证分析。2005年6月，中国科学院声学研究所声场声信息国家重点实验室在黄海海域进行了一次海底水平阵的声学实验，合作目标为一艘小型渔船。水平阵的有效阵元数为43个，阵元间距约为1.5 m。实验海区声速剖面如图14所示，海水深度为27 m。采样频率为4000 Hz，观测时间为10 min。实验过程中，目标近似做匀速直线运动，目标运动航向约为142◦，运动态势如图15所示。

目标方位历程和频域β-warping变换后的时域序列分别如图16(a)和图16(b)所示，距离特征量的估计结果如图16(c)所示，距离特征量的平均估计误差为4.37%。目标航向估计结果如图16(d)所示，通过实验数据处理结果可以看到，本文方法有效地缩短了航向估计的收敛时间，与仿真研究得到的结论一致。文献[5]和本文方法的收敛时间分别为6.5 min和3.5 min。

图14 实验海区声速剖面Fig.14 The sound speed profile of the experiment

图15 实验过程中的目标与观测平台的运动态势Fig.15 The motion state of target and observer platform for the experiment

图16 实验数据处理的目标航向估计结果Fig.16 The course estimation results for the experiment

5 结论

针对单一静止观测平台的目标航向估计问题，常规纯方位目标航向估计方法不仅需要目标保持匀速直线运动，而且航向估计的收敛时间较长，估计精度较低。针对此问题，本文提出了一种利用频域β-warping变换的浅海目标航向估计方法。该方法首先通过频域β-warping变换估计距离特征量，根据几何关系，利用目标方位和距离特征量确定目标航向，再利用渐近无偏最小二乘方法对目标航向进行估计。数值仿真和实验数据处理结果表明，在浅海水平不变波导远场条件下，对于单一静止的观测平台，该方法无需目标保持匀速直线运动，对直航运动的目标均可以进行可靠地航向估计。同时，该方法航向估计性能与观测时间内的平均方位变化率密切相关。复杂浅海环境下的方法的适用性是下一步研究的重点。

致谢感谢参加实验的全体人员，他们的辛勤工作为本文的科学研究提供了宝贵的实验数据。