高斯波对阻抗边界下离轴球形粒子的声辐射力

臧雨宸， 冀瑾皓

（1.中国科学院 声学研究所，北京 100049；2.中国科学院大学 物理科学学院，北京 100049）

与电磁场一样，声场携带有一定的动量。 当声波与物体发生相互作用时会产生反射、吸收等现象，往往会伴随着动量的转移。因此，物体受到了声场的力的作用，称为声辐射力。声辐射力的概念自提出以来，便迅速引起了声学界的重视，并在医学超声、材料科学和航天工业等领域得到了越来越广泛的应用。 1969 年，弹性粒子的声辐射力计算被Hasegawa 等人顺利完成[1]。 1990 年，J Wu 等人计算得到了聚焦波束下粒子的声辐射力[2]。 进入21 世纪以来，关于粒子所受声辐射力的研究方法又有了重大突破。 2005 年，F G Mitri 等人尝试计算得到了平面驻波声场和类驻波声场下柱形粒子的声辐射力特性[3]。 2006 年，J Lee 等人利用声线理论，研究了流体介质中任意位置的声辐射力特性，并验证了所谓“声捕获力”的可能[4]。 2009 年，F G Mitri 等人计算了贝塞尔声束对刚性球的声辐射力[5]。 2011 年，Silva 等人将其扩展到任意波束，大大拓宽了粒子所受声辐射力的应用范围[6]。2013 年，陈东梅等计算了高斯波束对水中球形粒子的声辐射力[7]，宋智广等计算了高斯波束对水中柱形粒子的声辐射力[8]。 2017 年，乔玉配等在自由空间的基础上增加了阻抗边界，得到了此时柱形粒子的声辐射力，并尝试讨论了粒子与边界距离大小等因素对声辐射力的影响[9-10]。 然而，纵观已有的研究结果，大多数结论基于粒子位于声轴的情形，这大大限制了有关理论的实际应用。 笔者基于声波的散射理论，通过有限级数法将高斯波束展开为球函数的形式，推导得到了阻抗边界下高斯波束对于离轴球形粒子的声辐射力公式，绘制刚性球和液体球的声辐射力函数曲线，并讨论了频率、粒子与边界距离、束腰半径和离轴角度与距离等各因素对声辐射力函数的影响。

1 理论

考虑半径为a 的球形粒子位于理想流体中的阻抗边界附近，粒子中心到边界的距离为d。 根据镜像原理可知，边界的存在可以等效为在其另一侧存在镜像波和镜像粒子，镜像粒子与边界的距离也为d。 一束高斯波沿z 轴正方向传播。以小球球心为原点O，高斯波束束腰中心的坐标为（0，y0，z0）。同时，以镜像小球的球心为另一坐标原点建立镜像坐标系图1 为此时的物理模型。

图1 阻抗边界下离轴球形粒子的声散射示意图

1.1 波束因子的计算

严格来讲，高斯波束的波阵面并不是一个平面，但是在束腰附近，可以近似作为平面来处理。入射高斯波束的速度势函数表示为

式中：φ0为速度势的幅值，k 为波数，w0为高斯波束的束腰半径，此处略去时间因子。 设

在yoz 平面内，φ=0，上式可以简化为

将高斯波束在球形粒子的中心处按照球函数进行级数展开

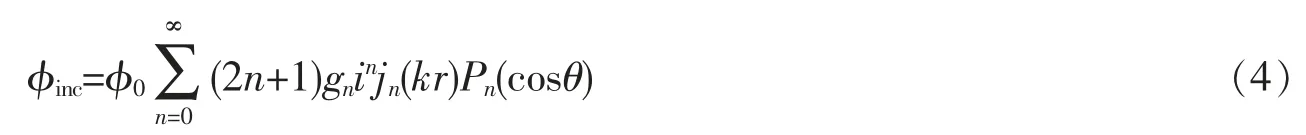
式中： jn(·)为n 阶第一类球贝塞尔函数，Pn(·)为n 阶勒让德函数，r 为球坐标系下的径向坐标，gn为入射高斯波束的波束因子。 参照在轴高斯波束中波束因子的计算方法[11]，可以得到，当n 为偶数时，波束因子为

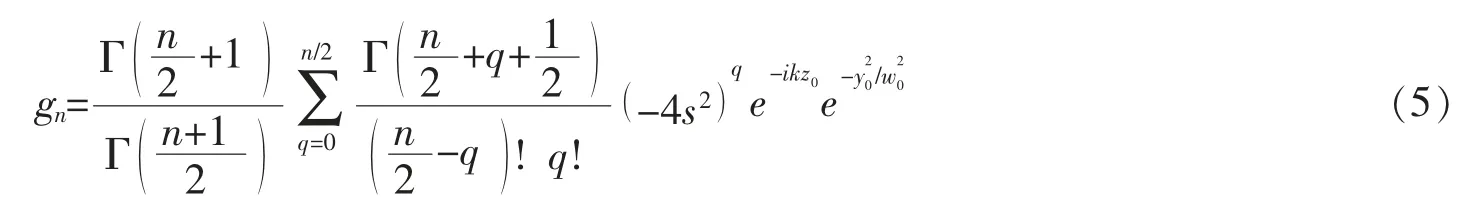
当n 为奇数时，波束因子为

式中：s=1/kw0。

1.2 散射系数的计算

得到了波束因子，可以用它来表示空间中存在的所有声场。 阻抗边界的反射波在坐标系（r，θ，φ）中可以表示为

式中：Rs为边界的声压反射系数。

球形粒子的散射波在坐标系（r，θ，φ）中可以表示为

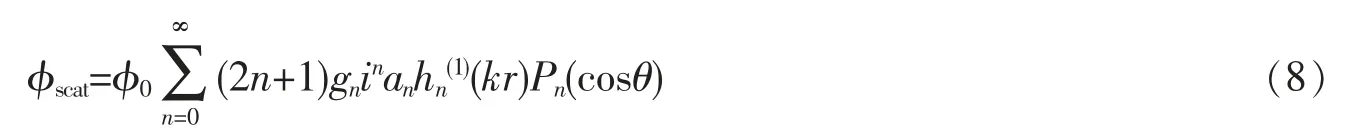
如果粒子材料的声阻抗足够大，表面可以看成刚性边界，则粒子内部不存在声波，表面径向速度为零，即

为了利用边界条件求得散射系数，首先利用球函数的加性定理将镜像粒子的散射波改写为

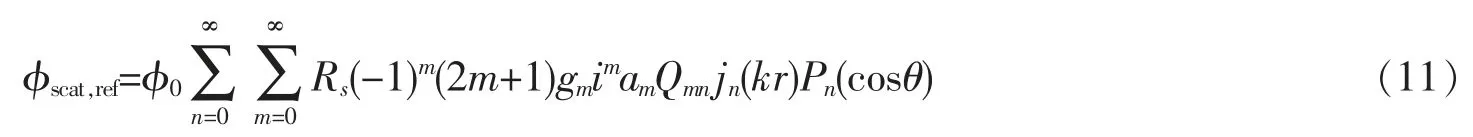
式中：Qmn的表达式可以在参考文献[12]中找到。

综合上述各式，可以得到声场中的总速度势为

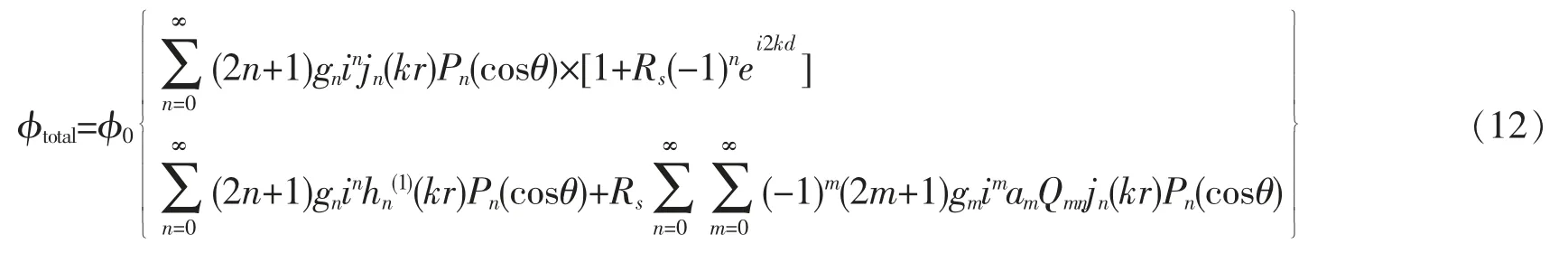
引入如下定义

则式（12）可以整理为

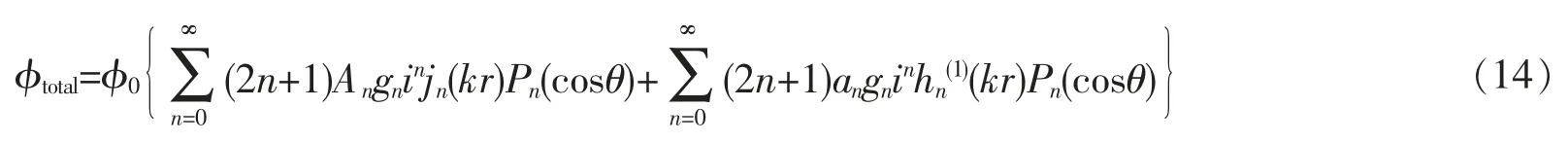
再根据速度势与质点速度的关系，得到径向速度表达式为

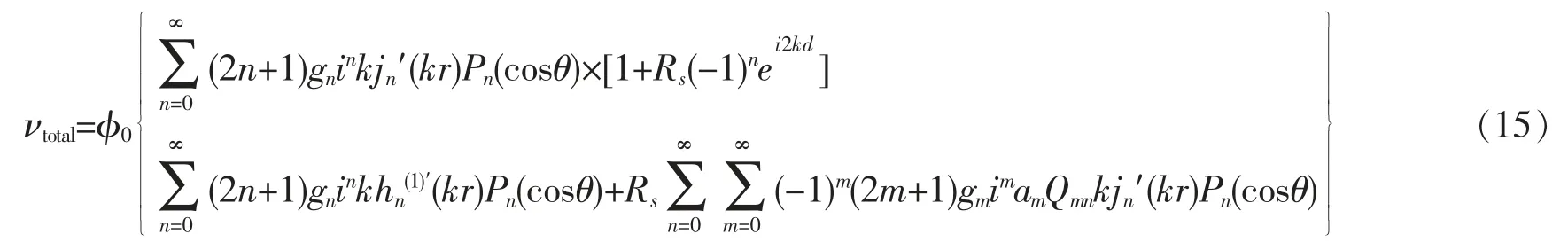
由式（15）和边界条件（10）可以得到散射系数an。

如果粒子材料的声阻抗不满足表面刚性的边界条件，则必须考虑粒子内部折射波的存在，其速度势可以写成

式中：Bn为折射波速度势的幅值，依赖于粒子表面的边界条件。 此时式（8）显然不再成立，应以表面处声压和径向速度连续取代之，即

式中：pl和νl分别表示折射波的声压和速度势。 式（17）中各量皆可以很容易地通过速度势函数求得，这里不再赘述。 根据此组边界条件，可以计算出an和Bn。

1.3 声辐射力的计算

理想流体中粒子所受的声辐射力可以表示为[1-10]

式中：vn和vt分别为法向和切向速度分量，ρ0为流体介质的密度，c0为流体介质中的声速。

根据式（18），可以得到在声波传播方向的声辐射力为

式中：ψ=Re（φtotal）。

将式（12）代入，计算可得轴向声辐射力可以表示为

式中：E 为声波的空间能量密度，S 为球形粒子的横截面积，Yp为声辐射力函数，表示单位能量密度和单位横截面积所受到的声辐射力大小，其表达式为

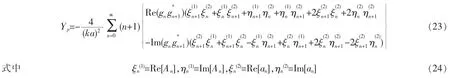
2 数值模拟

根据式（23）可以进行入射高斯波束对阻抗边界下离轴球形粒子的声辐射力的数值仿真。 假设粒子周围的流体介质是水，且将水看成理想流体。在液体球形粒子的情况下，假定粒子内部充满油酸。水和油酸的相关声学参数见表1。

表1 水和油酸的相关声学参数

2.1 不同边界反射系数下的声辐射力函数曲线

假定束腰宽度w0=3λ，粒子中心与束腰中心的距离d0=λ，d0与z 轴的夹角θ=π/6。在粒子与阻抗边界距离d0=2a 的情况下，对不同反射系数下粒子在声场中受到的声辐射力函数进行仿真，结果如图2 所示。 图2（a）和2（b）分别显示了刚性球和油酸球的声辐射力函数随ka 的变化曲线。 可以看出，不论是刚性球还是油酸球，声辐射力在ka 比较小时变化较剧烈。 值得一提的是，在某些频率处可以出现负向的声辐射力，此时粒子会被声波向声源的方向吸引。在ka 比较大时，声辐射力在一个稳定值附近出现小幅振荡，这是由于粒子的散射波和边界的反射波之间复杂的干涉现象所引起的必然结果。 随着反射系数的增大，声辐射力的峰值减小，但振荡峰值的位置并不因此而改变。对比图2（a）和2（b）可以发现，油酸球的声辐射力峰值远小于刚性球，且其峰值位置也有所不同。

图2 不同反射系数下声辐射力函数Yp 随ka 的变化

2.2 粒子与边界的距离对声辐射力的影响

假定束腰宽度、粒子中心离轴的距离和角度均保持不变，ka=0.5，对不同反射系数下刚性球和油酸球所受的声辐射力随kd 的变化进行仿真，结果分别如图3（a）（刚性球）和3（b）（油酸球）所示。可以发现，在ka 固定时，声辐射力函数随kd 的变化类似于正弦曲线，呈现出明显的周期性，并且声辐射力函数的峰值随着反射系数的增大而增大，但反射系数的改变并不影响曲线的周期。对比图3（a）和3（b），油酸球的声辐射力函数周期与峰值都小于刚性球。 这些和2.1 中得到的结论是一致的。

2.3 束腰半径对声辐射力的影响

为研究高斯波束的束腰半径对于声辐射力的影响，固定边界的声压反射系数Rs=0.5，粒子与边界的距离d=2a，粒子中心离轴的距离和角度不变，对不同束腰半径下的声辐射力进行仿真，刚性球和油酸球的结果分别如图4（a）（刚性球）和4（b）（油酸球）所示。 仿真的结果表明，束腰半径对于声辐射力的影响主要体现在ka>2 时，即中高频附近。 随着束腰半径的增加，中高频处的声辐射力函数在不断增大，并且最终趋近于平面波入射的情况。

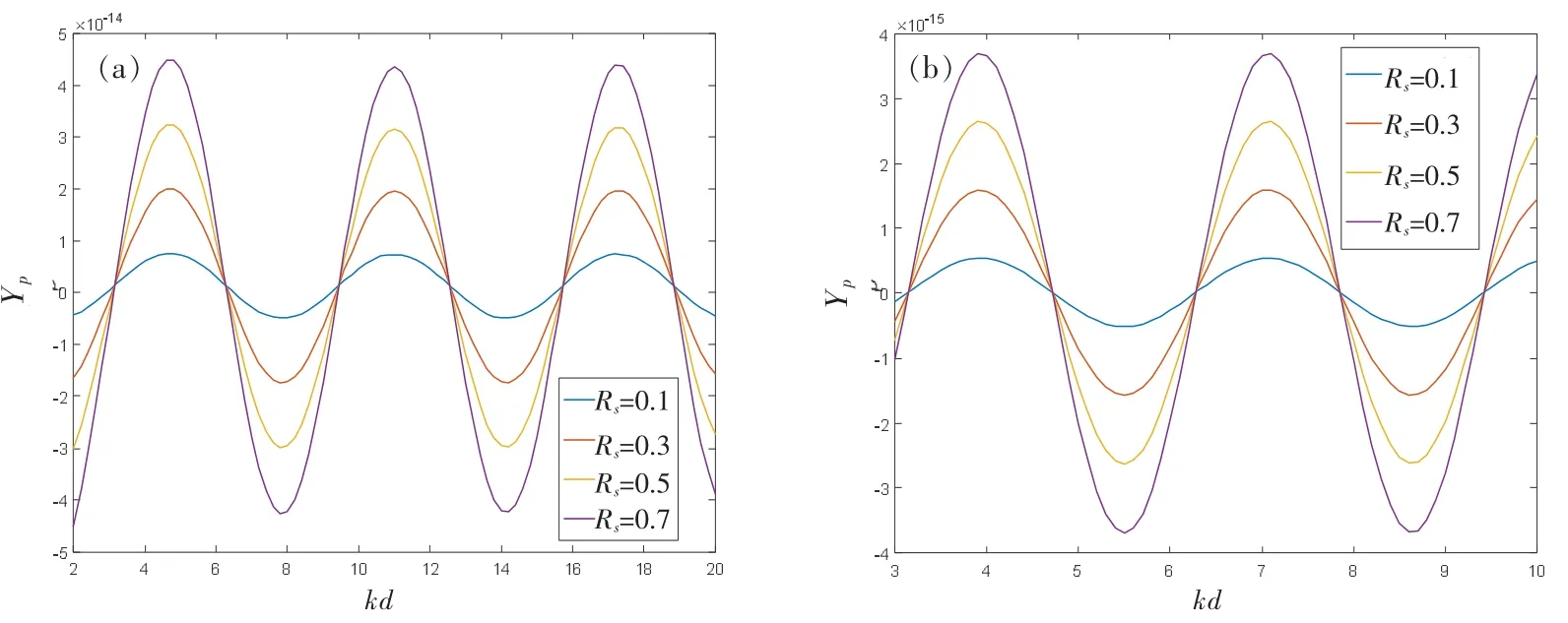
图3 不同反射系数下声辐射力函数Yp 随kd 的变化

图4 不同束腰半径下声辐射力函数Yp 随ka 的变化

2.4 离轴距离与角度对声辐射力的影响

在粒子中心偏离传播轴时，离轴的距离与角度对于声辐射力显然是有影响的。 固定ka=0.5，边界的声压反射系数Rs=0.5，粒子与边界的距离d=2a，束腰宽度w0=3λ。 为了讨论方便，采用无量纲量kd0作为横坐标。当d0与z 轴的夹角变化时，分别绘出其声辐射力函数随kd0的变化曲线，刚性球和油酸球的结果分别如图5（a）和5（b）所示。 从中可以看出，无论d0与z 轴成何种角度，声辐射力函数的幅值都随kd0的增大而减小。 另一方面，当kd0固定时，声辐射力函数随θ 的增加而减小，并且当θ 较大时，声辐射力函数将以更快的速度衰减到零。 这些结论都是与直观相符的。

图5 不同角度下声辐射力函数Yp 随kd0 的变化

3 结语

计算了阻抗边界下高斯波束对球形粒子的声辐射力。 该文从声波的散射理论出发，根据镜像原理以及高斯波束的级数展开理论，结合球函数的加性定理，推导出了阻抗边界下高斯波束对于球形粒子的声辐射力解析表达式。在此基础上，对不同参数下刚性球和油酸球的声辐射力进行了数值仿真。仿真的结果表明，声辐射力函数在中低频处变化较快，在适当的频率处存在负向声辐射力的现象。 边界声压反射系数的改变会影响声辐射力函数的峰值，但不影响取峰值时的ka 大小。当其他因素保持不变时，声辐射力函数随粒子与边界的距离呈现周期性，且反射系数的变化并不改变曲线的周期。 束腰半径是描述高斯波束的重要特征，其对声辐射力函数的影响主要体现在中高频，当束腰半径不断增大，曲线越来越趋近于平面波的情形。 最后，粒子中心偏离传播轴的距离和角度对声辐射力函数曲线有着显著影响，距离越大，角度越大，声辐射力微弱。 此外，在相同的条件下，刚性球的声辐射力远大于油酸球。 文中的结果预期可以为实际的声操控和声学镊子的制备提供理论指导。