基于变分正则化的混合泊松-高斯噪声图像去噪方法综述
2020-09-24常慧宾
常慧宾,张 婕
(天津师范大学 数学科学学院,天津300387)
在图像观测中,实际图像在其形成、传输、接收或处理过程中会受到内部因素或外部因素的干扰,进而产生噪声,此外,输导过程中产生的误差或其他人为因素也会对图像造成不同程度的噪声干扰.噪声严重影响了图像的视觉质量和效果,给图像融合、目标识别和特征提取等后续的处理与分析工作带来极大不便.去除图像的噪声,还原其原本的特征,是图像处理领域中的一个重要问题.在众多类型的噪声中,高斯噪声(Gaussian noise)由于在数学上的易处理性而被广泛关注和研究.然而,在许多实际应用中,噪声分布更加复杂,高斯噪声无法对其进行准确模拟.近年来,许多研究开始关注非高斯噪声的去除问题,大量的非高斯噪声去噪模型被提出[1-3],其中,基于变分正则化方法的图像去噪模型,因其易于与图像特征信息相结合,便于图像信息向连续函数转换,以及具有完备的数学理论等独特优势而受到广泛关注[4-6].
由于光子计数和热噪声对探测器的影响,观测到的图像往往会受到混合型的泊松-高斯噪声(mixed Poisson-Gaussian noise)的破坏,因此混合泊松-高斯噪声的去噪问题被广泛研究[7-12].处理混合泊松-高斯噪声通常使用基于最大后验估计(maximum a posteriori,MAP)的方法.如,文献[13]利用MAP方法结合混合泊松-高斯噪声的性质提出了一个精确的泊松-高斯估计模型,证明了泊松-高斯噪声的非负对数似然(negative log-likelihood)函数模型的凸性及其梯度的利普希茨连续性(Lipschitz differentiability),并提出了一个收敛的原始-对偶算法.为了选择一个较为准确的混合泊松-高斯噪声模型,文献[14]提出了一个基于全变分(TV)正则化的非光滑的PDE约束的优化策略.由于利用数学方法直接对混合泊松-高斯噪声模型进行处理比较困难,为了简化估计,很多研究通常会利用简单的变换忽略泊松噪声部分或者高斯噪声部分,之后利用处理单一类型噪声的方法对混合泊松-高斯噪声进行处理.如,文献[15]提出了一个加权l2模型,该方法利用加权的高斯噪声对泊松噪声部分进行估计.此外,文献[16]使用Shifted-Poisson的方法来估计混合泊松-高斯噪声,通过对噪声图像进行平移变换将混合泊松-高斯噪声去噪问题转化为泊松去噪问题.文献[17-18]提出一种广义的Anscombe变换来处理混合泊松-高斯噪声,针对此变换,文献[19]提出了一个无偏差的逆变换,大大改善了处理效果.文献[20]提出了一种基于均方误差(MSE)的线性扩展阈值(LET)的纯数据自适应无偏估计(Poisson-Gaussian unbiased risk estimate,PURE)模型,该模型是在非贝叶斯框架下提出的.有一些较有意思的工作是基于广义的联合MAP估计的方法,证明了去除高斯噪声的ROF模型[21]可以与针对泊松噪声导出的TV-KL模型[1]结合在一起对混合泊松-高斯噪声进行处理.如,文献[22]针对相应模型提出了一个原始-对偶迭代算法;文献[2]提出了TV-IC模型,其本质上是通过松弛2个保真项之间的关系对文献[22]的工作进行了扩展.最近,研究者将兴趣集中在设计变分正则化模型的快速算法.如,文献[23]设计了针对精确混合泊松-高斯噪声模型求解的交替方向乘子(alternating direction method of multipliers,ADMM)算法;文献[24]通过引入双线性约束对TV-IC模型进行改写,在此基础上设计了不含内迭代的快速ADMM算法.
正则项的选择对于去噪效果有非常重要的影响.1992年,Rudin等[21]提出了基于变分法的TV正则化方法,该方法在去除图像噪声的同时,可以有效地保留图像的边界或轮廓等特征[24],从而尽可能使去噪后的图像与原始图像相似,在此基础上,大量的基于TV正则项的去噪模型被提出[2,22,26].
虽然TV正则项被广泛应用于图像去噪中,但在实际应用中,TV正则项容易引起阶梯效应(staircasing effect).一种去除阶梯效应的方法是利用图像梯度的Huber范数代替原有图像梯度的欧几里得范数,由此便导出了Huber正则项[27],其应用于图像去噪的效果在文献[28]中被证明;另一种去除阶梯效应的方法是利用以黑赛矩阵为基础结合全变分方法的正则项(TVH正则项)[29-30],该方法不仅能防止阶梯效应产生,而且可以对图像强度的空间变化进行更好地估计.此外,非局部全变分(NLTV)正则项[31]也常应用于图像去噪中,该正则项与图像驱动的梯度方向有关.字典学习K-SVD[32]和基于块匹配的滤波技术BM3D[33]进一步结合了图像块的稀疏性,也取得了较大的成功.近年来,随着深度学习技术的发展,一些研究[34]基于深度学习思想的正则化提出了新的去噪方法.总之,依据图像噪声的特性来设计合适的正则项是研究图像去噪技术的重点之一.
本文主要对基于变分法的混合泊松-高斯噪声去噪模型及相应算法进行综述,介绍了几类具有代表性的基于变分正则化方法的混合泊松-高斯噪声去噪模型,并总结了求解模型的常用高效数值算法,设计实验评估了不同模型的去噪效果,最后,讨论了该研究领域存在的某些问题,并对其发展方向进行了展望.
1 混合泊松-高斯噪声去噪模型
首先,简要介绍图像去噪建模中常用的MAP方法及单一噪声处理模型;然后,重点介绍基于变分正则化的几个重要的混合泊松-高斯噪声去噪模型:(1)基于MAP估计的精确泊松-高斯噪声估计模型[13];(2)通过一些简单代数变换转化为单一类型噪声的模型,如加权l2模型[10,15,35-36]、Shifted Poisson模型[16,37]、广义的Anscombe变换模型[17,19];(3)基于泊松-高斯数据的PURE模型[20];(4)基于广义MAP估计的TV-IC模型[2,22].
1.1 MAP方法及单噪声处理模型
图像去噪一类重要的方法是基于统计理论范畴的.考虑到贝叶斯理论[38-39]的重要性,本节主要对基于贝叶斯估计的图像去噪建模方法进行简单介绍.设f为给定的被噪声污染的图像,u为原始的干净图像,则贝叶斯定理可以表述为

其中:p(f|u)为似然密度函数;p(u)为原始干净图像的先验密度函数;p(u|f)为后验密度函数.MAP估计就是在观测图像f已知的条件下求出使后验密度函数p(u|f)取最大值的原始图像u.由于p(f)已知,故对式(1)求p(u|f)的最大值即求下式的最大值,
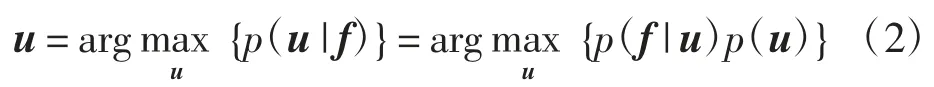
式(2)两端取负对数得
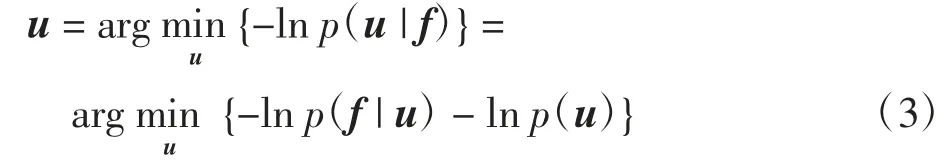
将其与相应噪声的概率密度函数及图像先验模型相结合,即可得到对应的变分图像模型.利用此方法,可推导出去除单一高斯噪声的ROF模型[21]

和去除单一泊松噪声的TV-KL模型[1]
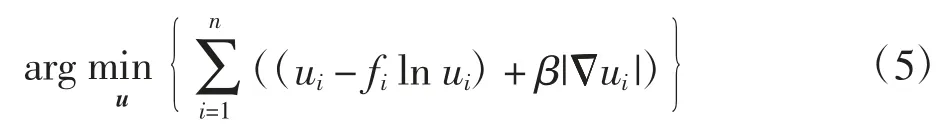
式(4)和式(5)中,‖·‖2表示L2空间范数,由Gibbs先验导出的项称为模型的TV正则项[21],另外一项是由似然密度函数导出的项,称为保真项(或数据拟合项),其与噪声的概率密度分布密切相关.
1.2 混合泊松-高斯噪声去噪模型
设u为原始干净图像,f为混合泊松-高斯噪声污染的图像,即:

其中:vi~Poisson(ui),ηi~N(0,σ2).
基于MAP估计,文献[13]给出了精确的泊松-高斯估计模型
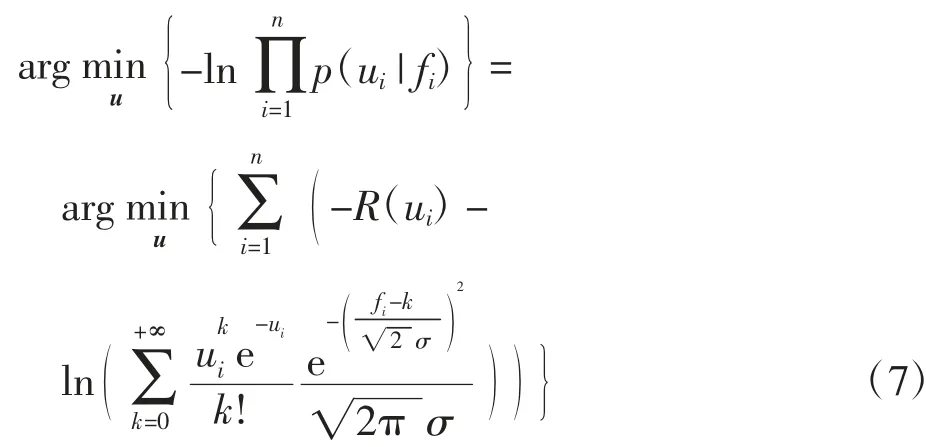
其中R(u)为正则项.该模型对于混合泊松-高斯噪声的估计十分精确,但由于该模型需求解函数项级数的极小化问题,难以得到数值上的精确解,因此有较多工作研究低复杂度求解的近似模型,特别是借助简单的代数变换将混合噪声转化为单一噪声,如加权l2模型、Shifted-Poisson模型、广义的Anscombe变换模型等.
加权l2模型最早应用于图像的泊松噪声去除,其本质思想是将噪声理解为一个外加的扰动,利用高斯分布对其进行估计,相应的模型为
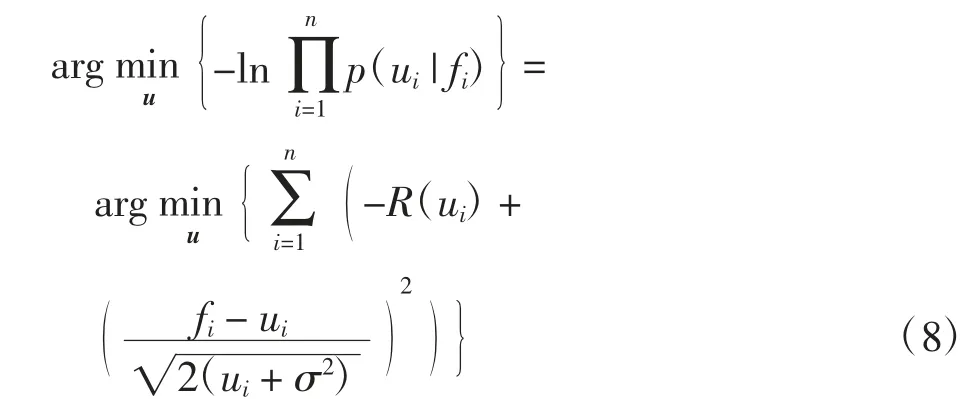
广义Anscombe变换模型[17-18]是基于对泊松分布数据“高斯化”的非线性变换[40](即Anscombe变换)的推广而得到的,具体的变换公式为
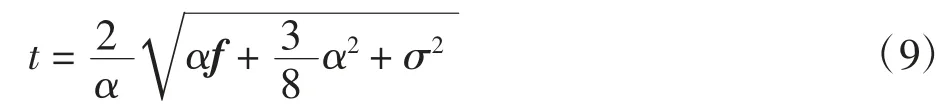
其中α为权重.此变换可将混合泊松-高斯噪声的去噪问题转化为高斯噪声去噪问题,因而一些针对高斯噪声的精确去噪模型[21,41]均可使用.进一步,为了使该模型的计算结果更精确,文献[19,42]提出了相应的准确的无偏逆变换,文献[43]提供了混合泊松-高斯噪声污染的荧光显微图像集,并利用广义的Anscombe变换法进行了去噪实验,将上述方法运用到了实际数据分析中.
与上述2种模型不同,Shifted-Poisson模型利用泊松分布估计混合泊松-高斯噪声中符合高斯分布的部分,将混合泊松-高斯噪声去噪问题转化为单纯的泊松去噪问题,相应的模型为
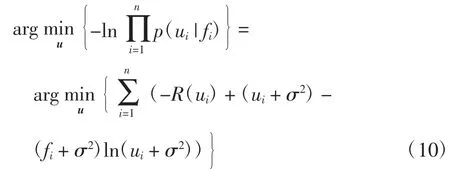
上述3种模型都是利用简单的估计,忽略混合噪声中的泊松噪声部分或高斯噪声部分,利用单一型噪声模型对混合型噪声进行估计,这使得相应的模型求解变得简单快速,但这类模型对混合噪声的估计并不精确,因而它们的去噪效果还有进一步提升的空间.

的最小值.在实践中,显然不能得到干净的原图像u,所以真实的MSE值也无法得出并最小化.然而,借助泊松分布或高斯分布的统计性质,可以导出一个MSE值的无偏差估计

文献[20]由此给出了去除混合泊松-高斯噪声的PURE模型,该模型的求解主要使用LET方法,进而得到PURE-LET求解方法[20].
基于广义的联合MAP估计,文献[2,22]结合标准Stirling估计[44-45]提出了TV-IC模型
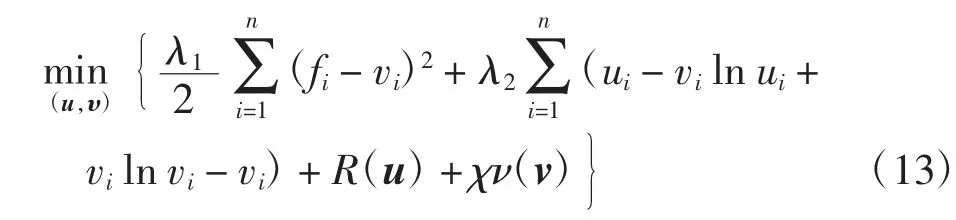
其中χν(v)为集合ν={v:vi≥0,∀i}的示性函数,即

该模型与精确估计模型类似,都是从MAP估计出发,且形式较为简单,因而TV-IC模型是目前计算代价较低,去噪效果较好的一个模型.该模型的推导过程运用了标准的Stirling估计,即利用Stirling公式的前2项来近似MAP估计中出现的lnvi!项,在vi的值较小时容易造成较大误差,因此,寻找更优的lnvi!的估计将会有效改进算法的图像重建质量.
1.3 模型小结
对前述各类基于变分法模型的保真项的具体形式进行简单总结,具体见表1,包括精确泊松-高斯估计模型(EPG)、Shifted-Poisson模型(SP)、广义的Anscombe变换模型(GAT)、PURE模型、加权l2模型(wl2)和TVIC模型.

表1 各种模型的保真项Tab.1 Fidelity terms of the models
由于篇幅有限,本文未覆盖EXP模型[10]、基于最小误差估计的MMSE模型[46]、将ROF与TV-KL相结合的模型[8].此外,随着深度学习技术的发展,一些研究者开始利用深度学习技术进行图像去噪[34,47].
2 求解混合泊松-高斯噪声模型的常用算法
本节介绍求解混合泊松-高斯噪声变分正则化模型的一阶优化算法,包括原始-对偶算法[22,48-49]、交替方向乘子(ADMM)算法[50](与之等价的有Split Bregman算法[15,48])以及半光滑牛顿(semi-smooth Newton,SSN)算法[2,14,51-52]等.
2.1 原始-对偶算法
原始-对偶算法是计算鞍点问题的一类有效算法,也被成功用于求解混合泊松-高斯噪声去噪模型,包括TV-IC模型[22]和精确的泊松-高斯估计模型[13,53]等.下面以TV-IC模型的求解[22]为例介绍该算法.
引进约束z=u对TV-IC模型进行改写,并将原始-对偶算法应用于该最优化问题的计算,
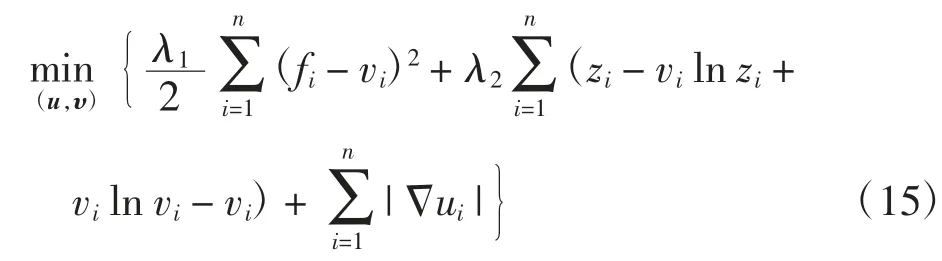
引入TV范数的预对偶形式[54],上述问题可以变成如下最大-最小(或鞍点)问题
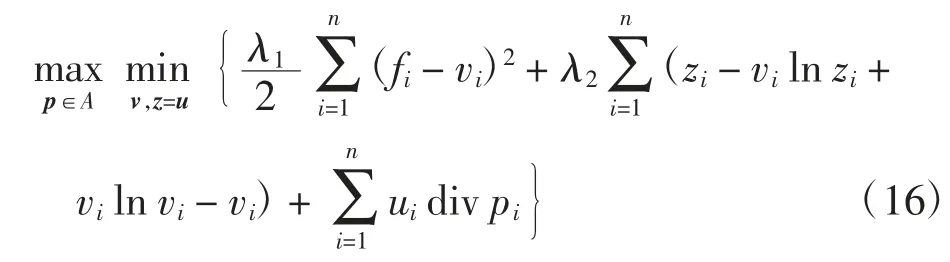
其中:div为散度,
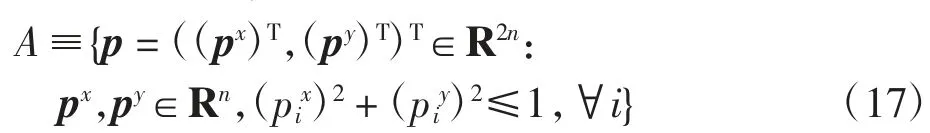
为了求解该带约束的最大-最小问题,进一步引入拉格朗日乘子y建立如下增广拉格朗日泛函优化模型,以消去对变量z、u的约束,
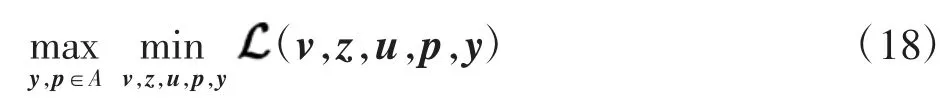
其中
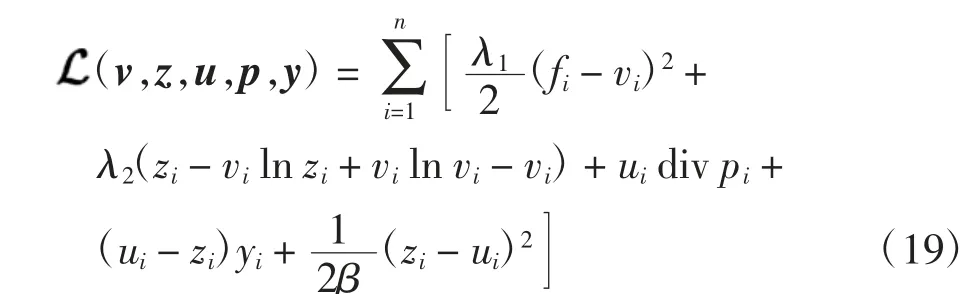
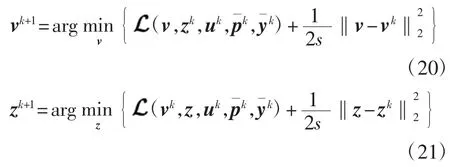
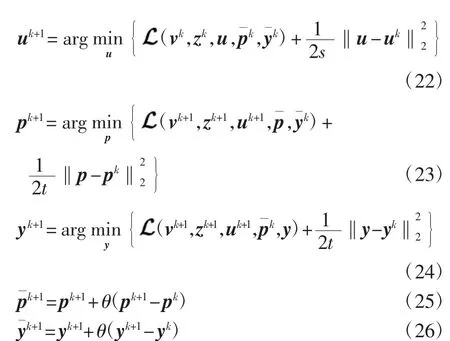
在具体进行求解时,由于该算法在求解v子问题(20)时涉及一个牛顿内迭代,故该算法比较耗时.后面会介绍一种新算法[24],该算法通过引入双线性约束来巧妙地规避此类问题.
2.2 ADMM算法
ADMM算法是图像处理的常用算法之一,它结合了对偶分解[55]和增广拉格朗日算法[56-58]的优点,是求解带约束优化问题的一种有效算法.文献[23]将ADMM算法应用于精确混合泊松-高斯噪声模型的求解.文献[37]将其应用于对惩罚加权的最小二乘模型的求解,该模型属于加权l2模型中的一种.TV-IC模型是目前对于混合泊松-高斯噪声刻画较好,较为成熟的方法,文献[24]通过引入双线性约束改写该模型,并利用ADMM算法求解新的模型,其相应算法如下.
通过引入双线性约束ui=viwi,将式(13)改写为如下等价的约束优化问题
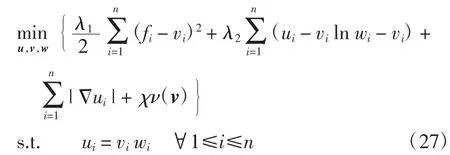
显然,此优化问题中vilnvi消失,因此,可以针对具有显式解的v子问题和w子问题设计快速算法.引入乘子Λ,上述约束优化问题的广义拉格朗日函数为
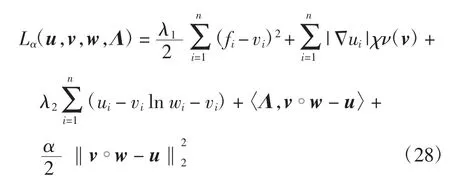
其中α>0为算法的罚参数.
已知前一次的迭代值(uk,vk,wk),ADMM算法通过求解如下3个分别关于u、v、w的子问题及乘子更新得到新的迭代值(uk+1,vk+1,wk+1):
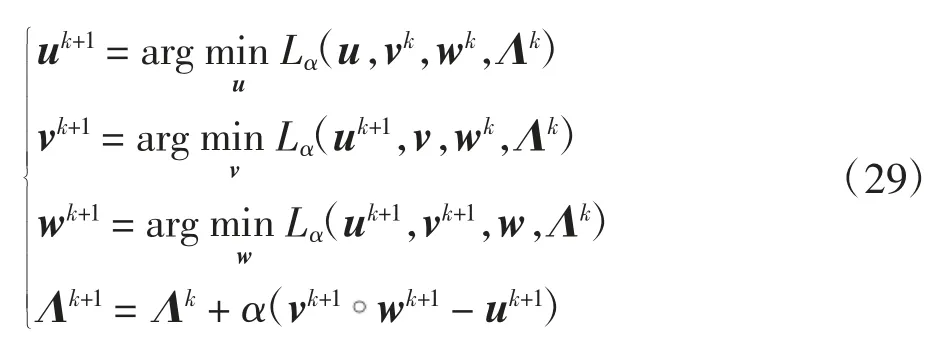
u子问题为
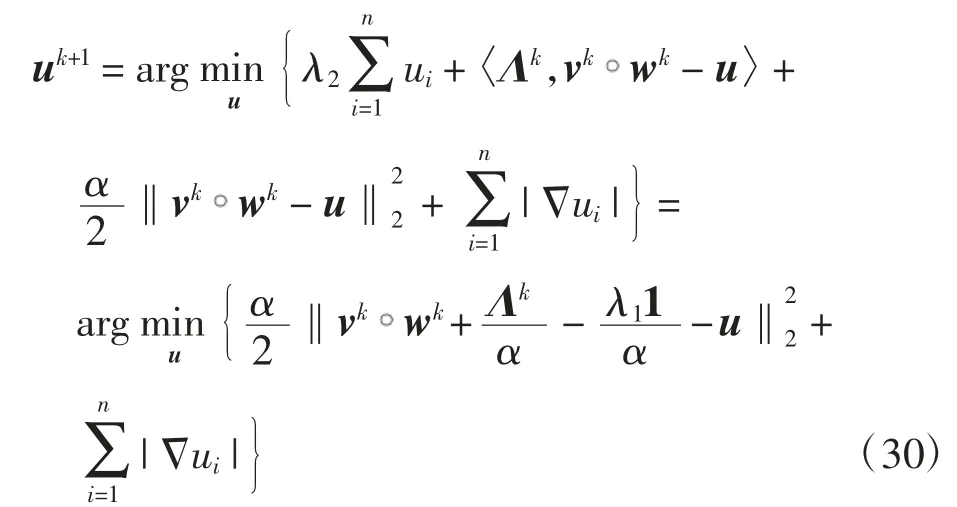
其中1∈Rn是一个所有元素均为1的向量.这是一个标准的TV-L2问题[21],可以利用针对原始-对偶形式的全变分最小化问题的梯度投影算法[54]进行求解.
v子问题为

在这个最优化问题中,可以分别对v的每一个元素进行独立求解,即可以考虑简化的优化问题
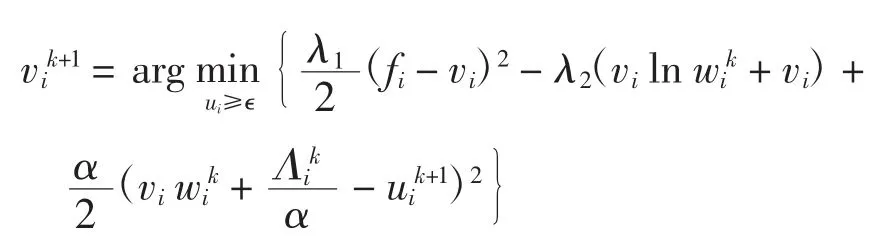
v子问题的最优解为
vk+1=max(ϵ1,k+1)
其中
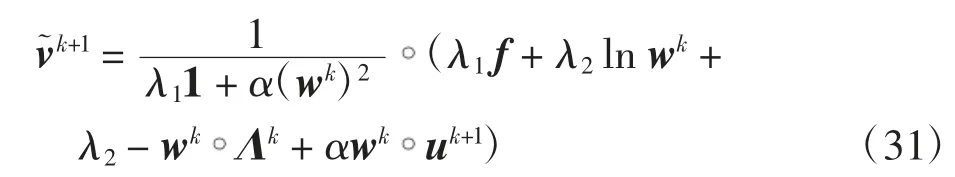
对应于无约束最优解.
w子问题为
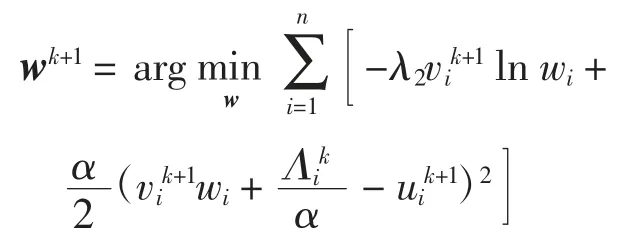
这是一个凸优化问题,其简化的优化问题为
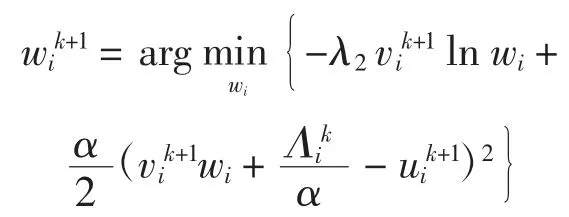
简化问题的最优条件为
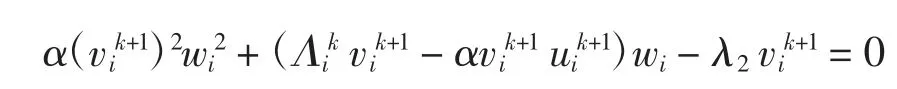
由此可得其显式解为

由此可以进一步简化v子问题的计算,将式(31)写为如下形式,
因此有
通过上述展示不难看出,基于双线性约束的ADMM算法的每个子问题都具有闭形式的解,与文献[22]中针对TV-IC模型设计的原始-对偶算法相比,该算法不包含任何内迭代,计算速度更快,更有效.此外,在解决一些凸优化问题及非凸优化问题时,ADMM算法的收敛性及收敛速度均可得到[59].另一种常用的Split Bregman算法与之等价,文献[15]利用Split Bregman算法求解了加权l2模型.
2.3 SSN算法
文献[2]提出了TV-IC模型,并运用SSN算法对其进行了求解.为方便,文献[2]用Huber正则函数[27]作为模型的正则项,并在模型中加入惩罚项来代替约束项.原模型被改写为如下形式
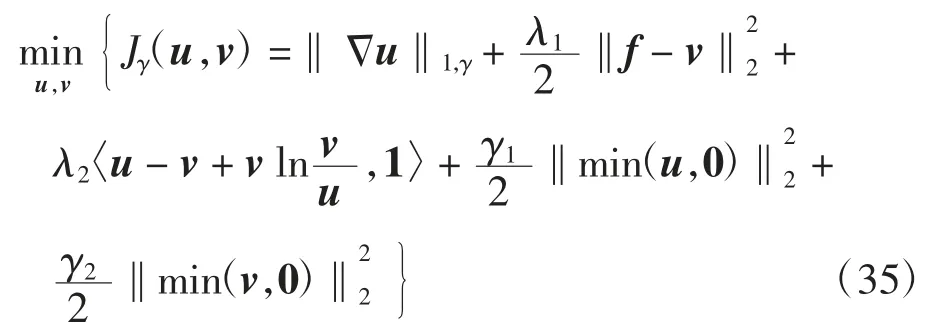
其中:‖Δu‖1,γ为Huber正则项,矩阵间的所有运算均为对应元素的点点运算.上式对应的最优性条件为
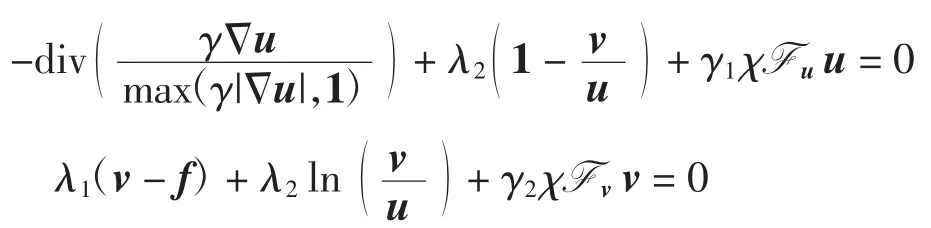
其中:χFu和χFv分别为集合Fu={u:u<0}和Fv={v:v<0}的示性函数.
2.4 算法小结
对于求解混合泊松-高斯噪声变分正则化模型,一阶优化算法的优点是每次迭代的代价较低,模型能够在很少的迭代步数内得到较好的重建图像.
SSN算法收敛速度快,较少的几步便可收敛到模型最优解(误差小于机器精度),但是其内存消耗较大,每步的计算代价较高.因而,在将来的研究中,值得探索如何设计低求解复杂度、收敛速度快的新算法.同时,在算法推导的过程中,不可避免地引入了一些人工参数,这些参数影响了实际的图像重建效果和算法的收敛速度.因而,在实现算法时不得不面临调参的问题,影响了算法的推广和应用.
在现有的一阶算法中,ADMM算法是目前图像处理中常用的算法之一.近来一些学者将ADMM算法应用于非凸优化模型的求解[60-62].文献[24]引进双线性约束对TV-IC模型进行改写,并利用ADMM算法求解改写后的模型,在保证求解效果的情况下大大提升了求解速度.然而,由于双线性约束的存在,改写后的模型是非凸的,现有的针对求解非凸问题ADMM算法的收敛性分析并不能直接应用于该问题的分析,特别是受限于现有的收敛性证明技术,无法在理论上证明相应提出的全分裂算法的收敛性.因此,针对求解非凸问题的ADMM算法的收敛性分析具有非常重要的意义.
此外,还有一些算法被应用于混合泊松-高斯噪声模型的求解,如阈值函数的线性展开方法[20]、EM(expectation-maximization)算法[7]、小波变换和余弦变换[20],以及基于热流(heat flow)的算法[63]等,这些算法不具有一般性,这里不再详述.
3 数值实验
为了对去噪效果进行更加客观地比较和描述,采用信噪比(SNR)对相关图像的噪声水平进行估计,其定义为
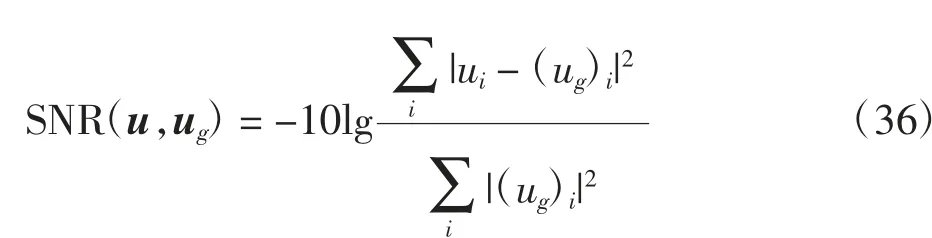
其中ug为未被噪声污染的干净的图像.
泊松噪声是依赖于图像强度的,噪声的大小取决于像素点的值,本文取一个度量因子η∈(0,+∞)来控制图像中泊松噪声的大小,η越大,泊松噪声越小,此外,采用高斯噪声分布的方差σ2控制高斯噪声的大小.实验采用的图像见图1.

图1 测试图Fig.1 Testing images
本文设计3组噪声水平(η=1、4、16,σ=0.1),其中高斯噪声水平固定,通过改变泊松噪声的水平控制混合噪声中泊松分布噪声和高斯分布噪声的相对强度.使用表1中涉及的6种模型对图1(a)进行处理,其中TV-IC模型结合了最新的ADMM算法,得到的SNR见表2,各模型的去噪效果见图2.由表2和图2可见,TV-IC模型优于其他模型,随着泊松噪声部分相对影响的减弱,Shifted-Poisson模型的效果相对减弱,广义的Anscombe变换模型和加权l2模型的效果逐渐增强,精确泊松-高斯估计模型和PURE模型的效果相对稳定.
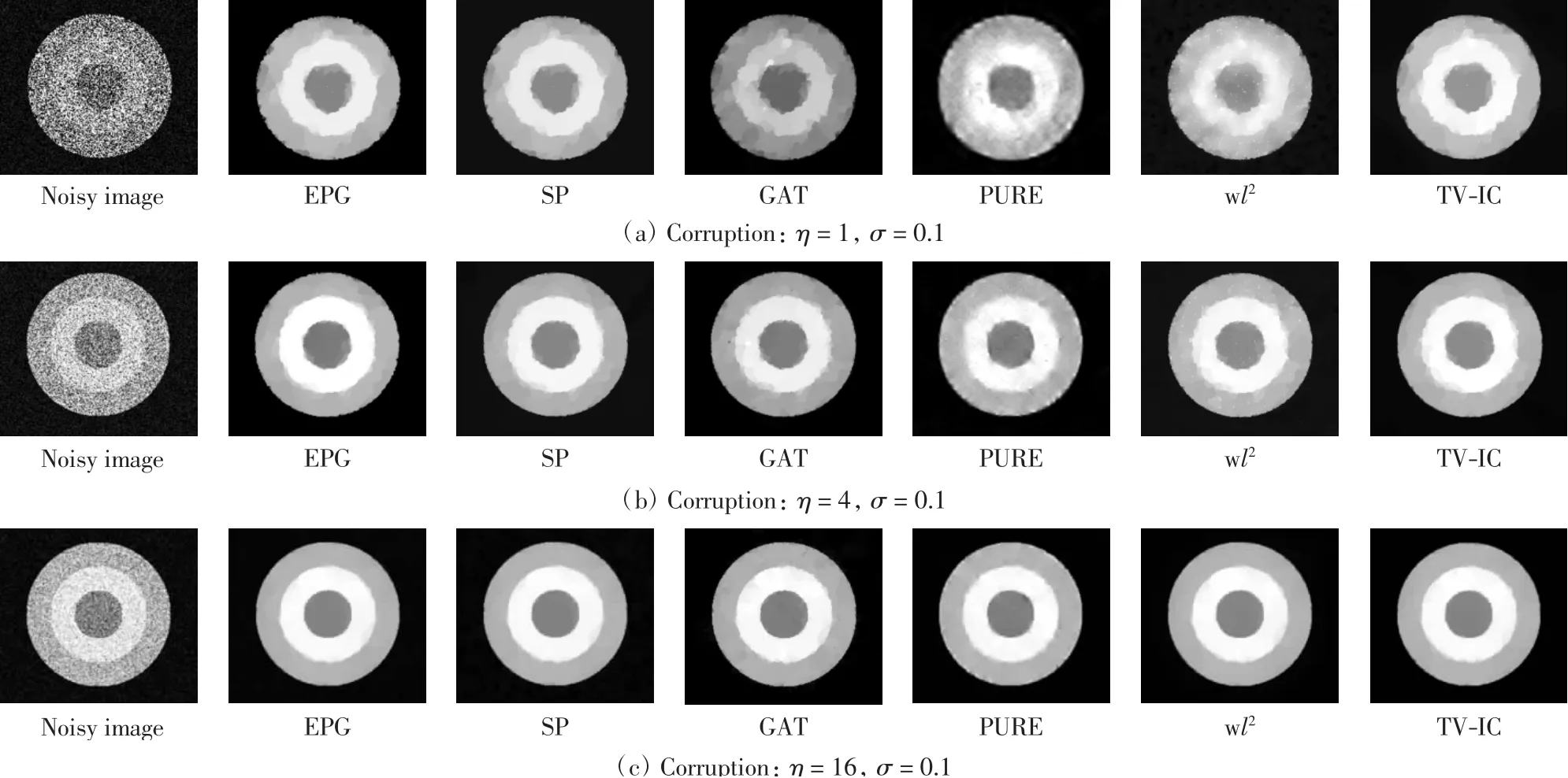
图2 各模型去噪效果Fig.2 Denoising performance for the models
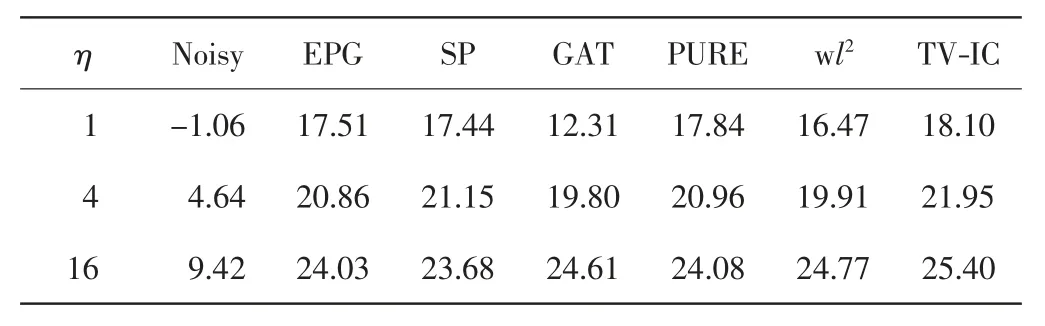
表2 各模型去噪后图像的SNRTab.2 SNR of denoised images for different models
此外,本文还探讨了不同正则项对去噪效果的影响.选择3类有代表性的正则项,包括局部低阶正则化(TV)、高阶局部正则化(HTV)和非局部块稀疏正则化(NLTV).为了体现非局部正则化的效果,选择一副包含较多纹理结构的图像(图1(b))进行实验,使用Shifted-Poisson模型,噪声水平统一设置为η=4,σ=0.1.实验结果见图3.

图3 Shifted-Poisson模型结合不同正则项的去噪效果Fig.3 Denoising performance for Shifted-Poisson model with different regularization terms
由图3可见,NLTV正则项的效果要优于HTV和TV正则项.NLTV正则项对纹理处理的效果较好,若要进一步提升图像重建效果,还可以考虑采用深度学习技术进行优化.
4 研究展望
关于混合泊松-高斯噪声去噪的变分正则化模型和算法的研究,本文认为有如下几个方面的问题值得继续探索.
(1)设计更有效的模型.虽然针对该类型噪声去噪的模型和算法比较丰富,但现有的模型都有一定的局限性.精确混合泊松-高斯估计模型虽然对噪声进行了较为精确的估计,但由于其目标函数为一个函数项级数,因此很难求出精确解;加权l2模型和Shifted-Poisson模型相较于精确混合泊松-高斯估计模型求解简单,但其只着重考虑混合噪声中的高斯分布部分或泊松分布部分,对混合噪声的估计不够精确;广义的Anscombe变换模型对逆变换的要求较高,简单的代数逆变换会造成很大的误差;基于均方误差估计的PURE模型对混合泊松-高斯噪声的概率分布性质考虑不充分,故其结果不够准确;TV-IC模型虽然充分考虑了混合噪声中的2种类型噪声的分布性质,但其应用的标准Stirling估计在vi的值较小时容易造成较大误差.综上,针对混合泊松-高斯噪声设计更加合理有效的去噪模型依旧是未来一个值得重视的研究方向.
(2)设计有收敛性保证的快速算法.得益于算子分裂算法的收敛性理论在非凸优化问题方面的进展,研究者可以刻画此类算法在该问题相关模型的收敛性,如,基于广义Anscombe变换可以设计新型的变分正则化模型,但是直接设计相应的算子分裂算法时,并不能保证每个子问题都有闭形式解.因此如何给出子问题的有效求解并保证其收敛性值得进一步探索.对于TV-IC模型,文献[24]引入了新型的约束条件,因而导出的算子分裂算法非常简单有效.然而,双线性约束的引入给分析算法(特别是全分裂格式)的收敛性带来了新的困难.因此,如何在理论上保证基于双线性约束优化的算子分裂算法的收敛性也是一个值得探索的方向.
(3)设计自动调参策略.本文回顾的模型和算法中不可避免存在多个参数,这对算法在处理实际数据中的实用性造成了影响,其中最基本的信息就是噪声分布的方差信息,因而如何自动估计实际污染图像的噪声分布信息是非常值得研究的.在此基础上,还需要进一步探索变分正则化模型的自动调参策略[52,64-66],与之相关的一个研究方向则是如何设计参数更少的快速收敛算法.
(4)研究高维以及非线性反问题成像.对于高维问题,如三维CT重建[41]、高光谱去噪[67]等,某些重要的成像问题[37,60,68],其测量数据与待重建的图像之间是非线性关系,其噪声也是直接作用于对变换域的非线性运算之后的,因而对于非线性反问题的研究也具有较高的应用价值.如何克服非线性和高维带来的困难,设计有快速收敛保证的算法是未来一个非常有意义的研究方向.
