第四希腊字母类乘积元的非平凡性

李园园，王玉玉

（天津师范大学数学科学学院，天津300387）

1 引言和主要结论

令S为奇素数p上的局部化球谱，A为模p的Steenrod代数，对球面稳定同伦群π*S新元素的发掘是同伦论的一个中心问题，Adams谱序列[1]是计算它的一个重要工具，相关学者对球面稳定同伦群中非平凡元素的发掘做了大量研究[2-7]，其中，文献[4]得到了与包含第三希腊字母类乘积元s+30密切相关的May谱E1项的一些结果，为该乘积元在Adams谱序列中的非平凡性打下基础，文献[6]考虑了涉及第三希腊字母类乘积元素γsξn的收敛性.

Adams谱序列的E2-项Adams微分为

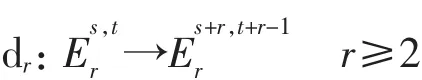
文献[10]得到了如下定理.

定理1当p≥11，0≤s＜p-4时，第四希腊字母类元素满足

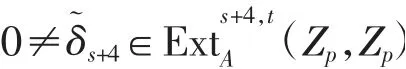
其中t=q[（s+4）p3+（s+3）p2+（s+2）p+（s+1）]+s.

本文主要结论如下.

定理2令p≥11，0≤s＜p-4，则Adams谱序列中的乘积元素满足

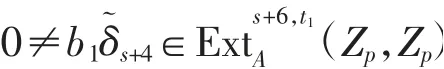
其中t1=q[（s+4）p3+（s+4）p2+（s+2）p+（s+1）]+s.

2 May谱序列

本节给出关于May谱序列E1-项的预备知识.由文献[11]的定理3.2.5知，存在May谱序列收敛到其E1-项

其中：E为外代数，P为多项式代数，

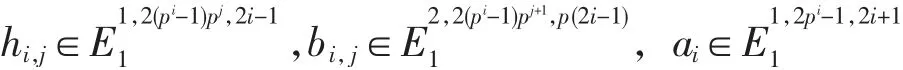
May微分为

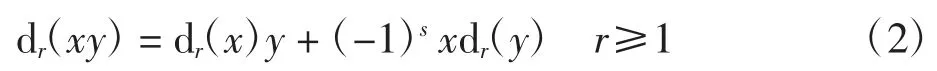
且有xy=（-1）ss′+tt′yx，x、y=hi，j、bi，j或ai.

第一May微分有公式

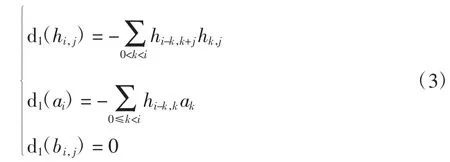
其中：i≥1，j≥0.具体发掘的元素的方法可见文献[12].

3 定理2的证明

首先给出相关引理.

引理1[13]令p≥11，0≤s＜p-4，第四希腊字母类元素可以被May谱序列中的元素a4sh4，0h3，1h2，2h1，3表示，其中t=q[（s+4）p3+（s+3）p2+（s+2）p+（s+1）]+s.

引理2令p≥11，0≤s＜p-4，则May谱序列的其中

证明在May谱序列中，考虑g=x1x2…xb y1…ym∈F1+b，t1，*，其中：xi=ai，yi=him jm.由于b=s，次数方程组为

由文献[12]可知，k的取值为（0，0，0），相应的c为（s+1，s+2，s+4，s+4），并且次数矩阵为

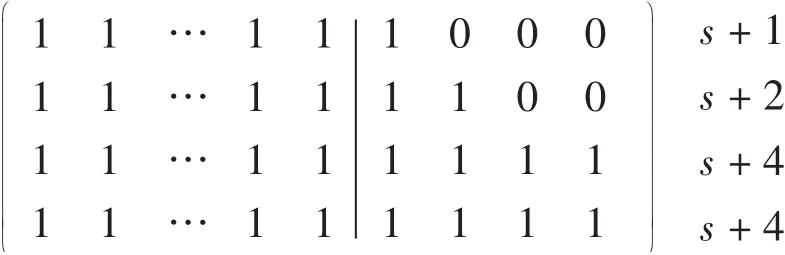
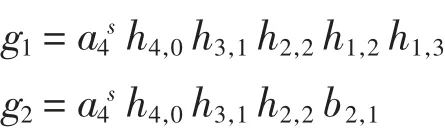
引理2得证.

引理3（1）令p≥11，0≤s＜p-4，元素可以被May谱序列中的元素

表示，其中

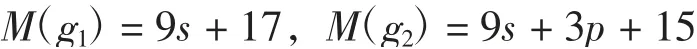
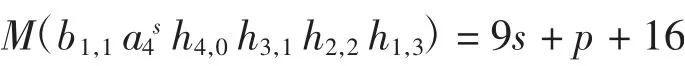
证明（1）b1，i在May谱序列里是永久循环且非平凡的，收敛到bi（i≥0）[13]，由引理1知，当0≤s＜p-4时在May谱序列里是永久循环且非平凡的，收敛到因此在谱序列里是永久循环且非平凡的，收敛到b

（2）由式（4）中第三May分次的计算可直接得出.

引理3得证.

定理2的证明由引理3的（1）知，元素可以被May谱序列中的元素表示.下面证明

由引理2有

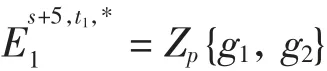
考虑生成元g1，有M（g1）=9s+17.由次数原因知g1在May谱序列里是永久循环且收敛到并有d（rg1）=0和因此

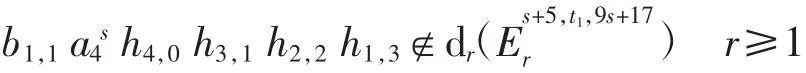
考虑生成元g2，有M（g2）=9s+3p+15，由式（1）及第三May分次知

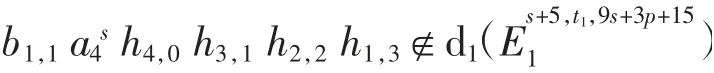
下面证明

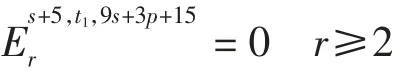
由式（2）和式（3）易得如下微分形式

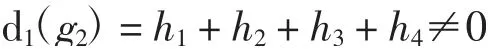
其中

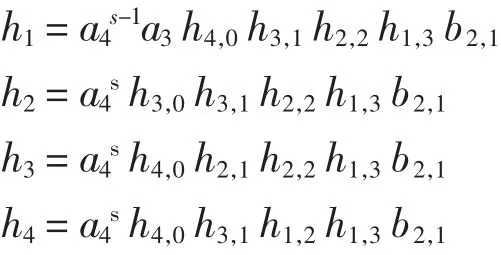
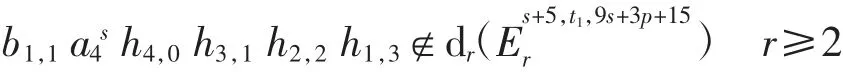
综上有

由以上讨论可得b1，1a4s h4，0h3，1h2，2h1，3在May谱序列里不是任何微分的像，故b1s+4≠0.定理2得证.

注对于第四希腊字母类乘积元素的研究仅限于非平凡性的证明，关于其是否收敛到球面稳定同伦群的非平凡性元素还有待研究.