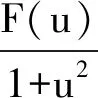关于一道不定积分考研题的解法注记

王成强

(成都师范学院 数学学院，四川 成都 611130)

引言

研究生入学考试数学科目中的试题，集甄别选拔功能、命题标准示范、教学引导等功能于一身.因此，考研中的数学问题往往是学习数学和教授数学的重要素材[1].不定积分理论是大学数学最重要部分之一[2-3]，与之相关的问题的解题思路灵活，结构多变，能很好地检测出学习者对大学数学学习情况，能很好地把握学习者开展后续学习的潜能.因此，在诸如大学数学的期末考试、考研数学考试、大学生数学竞赛等各类考试中，都会出现不定积分相关问题的身影[4-6].对典型不定积分问题开展一题多解的研究，能加深教师对该类问题的认识，从而将问题从不同视角展示给学生，进而能帮助教师改善课程教学效果[7].本文旨在对一道不定积分考研试题进行一题多解研究，该不定积分问题是2018年中国硕士研究生入学考试数学(一)与(二)的试卷中的第三题中的第1 小题(全卷第15小题)，完整内容表述如下：

文献[8]给出了问题(*)的5种解答方法，文献[9]给出了问题(*)的6种解答方法.本文拟给出问题(*)的12种解答方法，以期为大学数学课程中的不定积分理论的学习与讲授带来更多思考.本文的研究结果在很大程度上补充了文献[8] [9]研究的结果.

1 问题(*)的12种解法

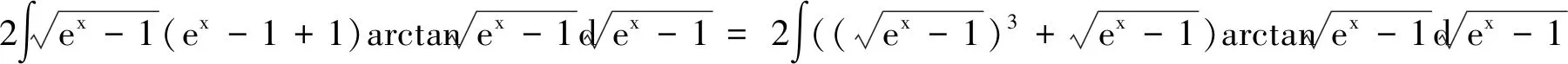
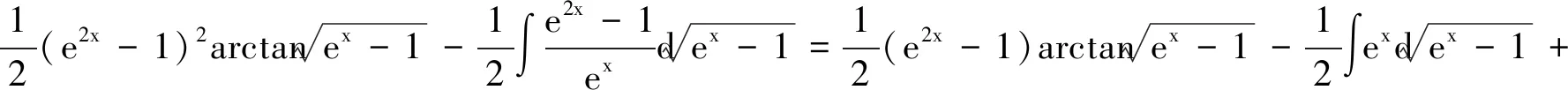
从解法1的思路可看出，问题(*)考查的是常规知识点.解法1能帮助学生加深对问题(*)本质的认识.解法1的求解思路可简要描述为微分恒等式

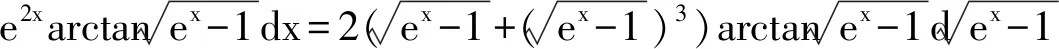
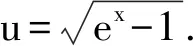
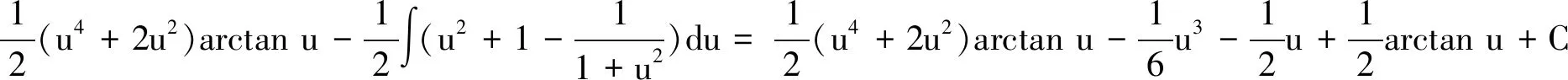
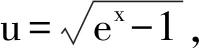
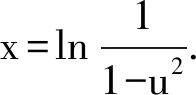
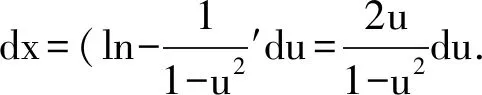
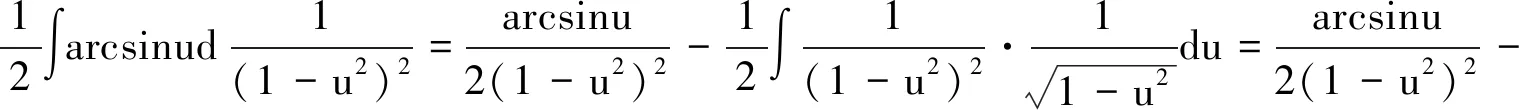
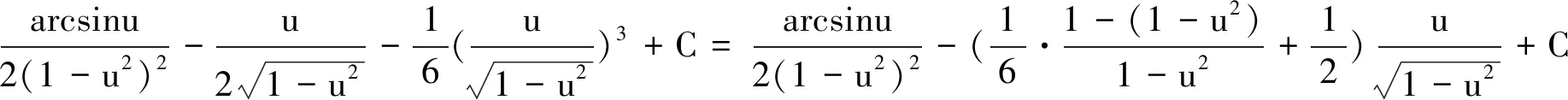
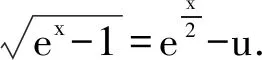
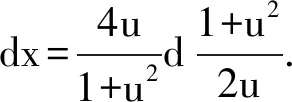
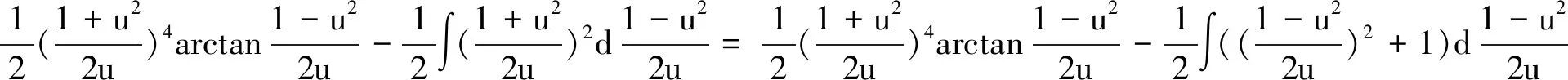
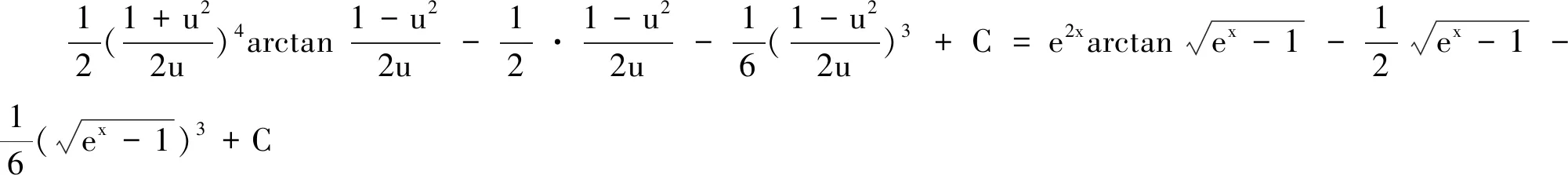
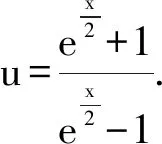
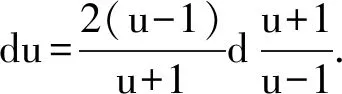
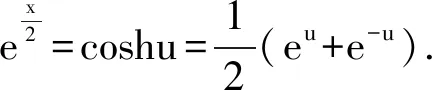
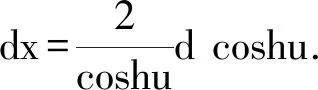
解法8 主要利用分部积分，有

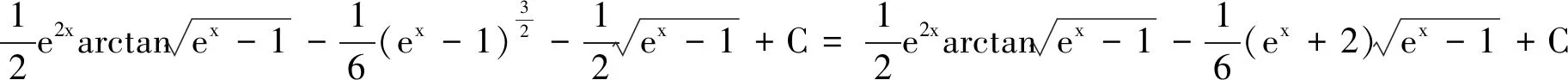
解法8的解题思路来自官方参考答案，它充分利用了指数函数的性质，因此，基于该方法的求解过程相对于其他方法的求解过程而言最为简洁.在官方参考答案(见文献[8]的解法4，文献[9]的解法1)具体步骤中分部积分法的用法如下：

在本文解法8中分部积分法的用法如下：

解法9 首先得到微分恒等式

利用分部积分法，有

于是

解法9 与解法8的求解思路相似，想法都是利用分部积分法.在解法9解答过程中，下述步骤最关键：

解法10 主要借助于分部积分法，有

于是

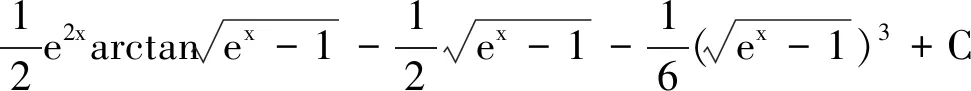
解法10 与解法8、9的求解思路相似，想法都是利用分部积分法.在解法10解答过程中，下述步骤最关键：

解法8、9及10中思路的更多应用可参见文献[4-6].

解法11 经开展微分运算可发现，有

换言之，有

于是有

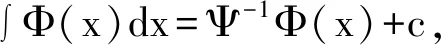
为求出待定参数c1，c2与c3，对上述等式两端同时求导，得

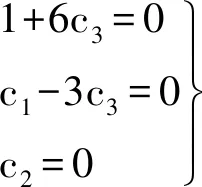
解法12借助于待定系数的想法计算不定积分，受到解法11的解答过程的启发与参考文献[8]中的解法5用到的求解思路有异曲同工之妙.除换元积分法、分部积分法之外，待定系数法在求解不定积分的有关问题中有独特的作用.

2 解法的比较分析

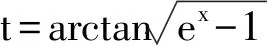
3 结语

本文对2018年中国硕士研究生入学考试试卷中的一道不定积分题分别给出基于整体代换法、换元积分法、分部积分法的12种解法，它们将问题(*)从不同侧面展示在读者面前，能加深读者对问题(*)的理解，从而引发人们对不定积分理论的学习与教学更多的思考.

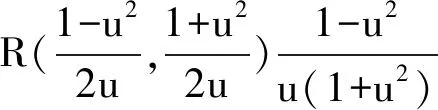
于是