由一道习题教学谈学生提出问题能力的培养

吴祖丰

上海市七宝中学 (201101)

培养学生提出问题的能力对培养学生的创新能力十分重要，也落实核心素养的有效途径，因而平时教学中对此类问题要予以重视，最好的方法就是紧密结合教材，通过对教材中问题由特殊到一般的拓展，培养学生提出问题的能力.本文通过一道教材中的题目，谈谈提出问题的常见方法，以期抛砖引玉.

在证明过程中用到三角形重心到顶点的距离等于到对边距离的两倍.如果联想到三角形是正三角形(把一般问题特殊化)，就可以提出：

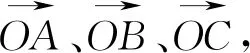
图1

在此基础上进行纵向推广到正多边形，可提出：

证明:n=3时，证略；

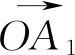
图2

把向量的起点放到坐标系原点，最容易想到三角函数，由此若把该题进行横向发散，可提出：

定义3 跳数度量：是指从源节点到目的节点所经过的节点的数目.跳数是一个重要的衡量指标，因为它的多少能够间接的反应出延迟时间的多少.

如果由三角形重心类比到空间，可提出：

问题4四面体A—BCD的各顶点与对面重心连线交于一点G，则顶点到G的距离与G到相应对面三角形重心距离之比为3∶1.

图3

同理可证顶点C与对面三角形重心连线过点G，即各顶点与对边重心交于一点G，且顶点到G的距离与G到相应对面距离之比为3∶1.

上述问题的数字特征明显，三角形的重心到顶点距离与到对边中点距离之比为2∶1，四面体的重心到顶点距离与到对面三角形重心距离之比为3∶1.维数增加1，比值增加1，这是很有意思的.

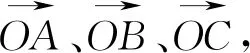
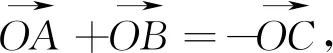
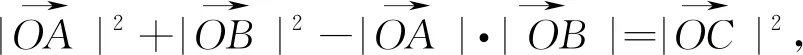
由上可见，既便一个简单问题我们提出了5个问题，甚至同学们可能会提出更多问题.当然，只是其中的一、两个，这样的训练对提升学生数学的综合素养是必要的.