基于区间Orthopair模糊Heronian测度的多属性群决策方法

陈艳如，王润玮，林志超，徐 鑫，周礼刚

(安徽大学 数学科学学院，安徽 合肥 230601)

多属性决策问题中通常会存在一定的模糊性和不确定性，使得对问题的评价或决策不够精准。为了描述事物的模糊性，在不确定环境下准确地评价问题，ZADEH[1]提出了模糊集理论。ATANASSOV[2]则提出了直觉模糊集的概念，在[0,1]区间上用隶属度和非隶属度描述事物。YAGER[3]提出了毕达哥拉斯模糊集的概念，以[0,1]区间上隶属度与非隶属度的平方之和小于1来刻画事物特征。但有时会出现平方和大于1的情况，例如0.72+0.92>1。在此基础上，YAGER[4]又提出了Orthopair模糊集的概念，以[0,1]区间上隶属度与非隶属度的q次方之和小于1来度量事物的模糊性。随后，JU等[5]提出了区间Orthopair模糊集，更加细致地度量了模糊性问题。

解决Orthopair模糊环境下的多属性群决策问题时，有时需要考虑属性之间存在的相关关系，并对已知的信息进行集成。王军等[6]利用Maclaurin对称平均算子集结模糊信息，提出了基于广义正交模糊集结算子的多属性决策方法。LIANG等[7]在贝叶斯决策的基础上，构建了Orthopair模糊决策粗糙集的基本模型，推理出了相应的三支决策方法。LIU等[8]将属性之间的相互关系与Heronian平均相结合，提出了Heronian平均算子及其加权形式。陈雯等[9]基于Theil不等系数提出梯形模糊相似测度，构建以梯形模糊相似测度最大化为目标的最优化模型获取属性的权重。关于两个Orthopair模糊向量之间的测度研究，LIU等[10]用余弦相似测度和欧式距离度量两向量间距离。

在解决区间Orthopair模糊环境中的复杂问题时，有学者针对实际问题提出了相应的相似测度和决策方法。如BELIAKOV等[11]提出的Heronian平均算子是一个经典的集成算子，但是Heronian平均算子还尚未被运用于描述区间Orthopair模糊信息的集成。刘焕章等[12]对Heronian平均算子进行了推广，提出了广义Heronian平均算子，将其与OWA算子相结合应用于银行对企业投资决策的实际问题中。刘卫锋等[13]提出了广义加权Heronian平均算子、三参量Heronian平均算子及其加权形式，并推广到语言决策中。

基于上述研究，笔者先定义了一种区间Orthopair模糊向量之间的加权余弦相似测度，并将其与广义Heronian平均加权算子相结合，提出一种新的区间Orthopair模糊Heronian测度，通过研究该测度方法的性质，最终提出一种基于区间Orthopair模糊Heronian测度的多属性群决策方法。

1 基本概念

定义1设X为一论域，称I={〈x,μI(x),vI(x)〉|0≤μI(x)+vI(x)≤1,x∈X}为X上的一个直觉模糊集。其中，映射μI:X→[0,1],x→μI(x)表示X中的元素x属于集合I的隶属度，映射vI:X→[0,1],x→vI(x)表示X中的元素x属于集合I的非隶属度。

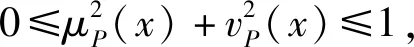
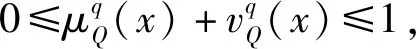
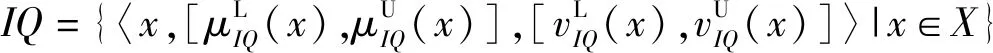
定义5设a=([μL,μU],[vL,vU])为一区间Orthopair模糊数，可定义如下得分函数S(a)和精确函数P(a)：

(1)

(2)

由上述定义可以看出，0≤S(a)≤1,0≤P(a)≤1。得分函数值或精确函数值越大，说明相对应的区间Orthopair模糊数越大。特别地，当a=([1,1],[0,0])时，S(a)=1；当a=([0,0],[1,1])时，S(a)=0。采用文献[5]给出的定理对区间Orthopair模糊数的大小进行比较。

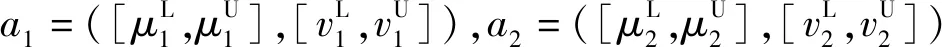
在多属性群决策问题中，属性之间有时会存在某些关系，而广义Heronian加权平均算子则是度量这些关系的一个十分有用的工具。

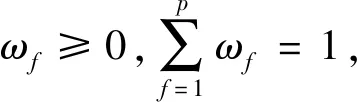
(3)

2 区间Orthopair模糊Heronian测度

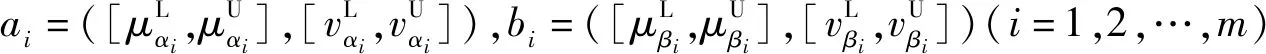
CIVqOF(α,β)=

(4)

定理2设X为一论域，α=(a1,a2,…,am),β=(b1,b2,…,bm)为两个区间Orthopair模糊向量，则α和β之间的余弦相似测度CIVqOF(α,β)满足以下性质。①有界性：0≤CIVqOF(α,β)≤1；②交换性：CIVqOF(α,β)=CIVqOF(β,α)；③自反性：CIVqOF(α,β)=1，当且仅当α=β时成立。

在对模糊数进行集结的过程中，不同的模糊数可能会对应不同的权重，因此区间Orthopair模糊环境下的加权余弦测度可定义为：

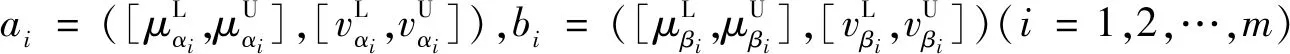
WCSIVqOF(α,β)=

(5)

定理3设X为一论域，α=(a1,a2,…,am),β=(b1,b2,…,bm)为两个区间Orthopair模糊向量，则α和β之间的加权余弦相似测度WCSIVqOF(α,β)满足以下性质。①有界性：0≤WCSIVqOF(α,β)≤1；②交换性：WCSIVqOF(α,β)=WCSIVqOF(β,α)；③自反性：WCSIVqOF(α,β)=1，当且仅当α=β时成立。

在多属性群决策问题中，通常需要考虑多个模糊向量与一个模糊向量或者多个模糊向量与多个模糊向量之间的关系。因此，可将问题转化成考量两个由模糊向量组成的模糊矩阵之间的相似测度。在集成多个模糊向量之间的相似测度时，考虑到不同的模糊向量对问题的影响程度不同，运用广义加权Heronian平均算子对相似测度进行集结。

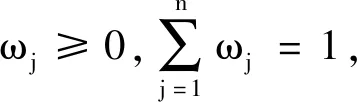
(6)

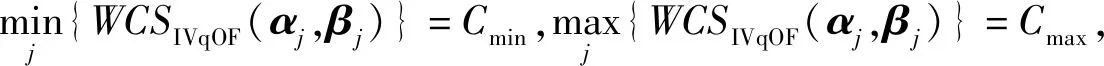
3 基于IVqOFWHCS测度的多属性群决策方法

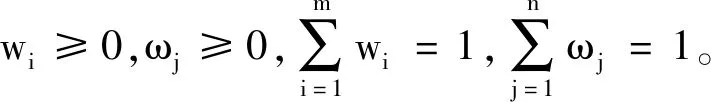
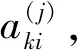
(2)因属性分为成本型和效益型两种，故需要对决策矩阵进行标准化处理，如式(7)所示。

(7)

(8)

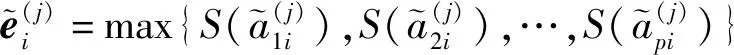
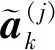
(9)

(6)利用IVqOFWHCS测度集结加权余弦相似测度，得到备选方案Fk的综合评价值rk(k=1,2,…,p)：

(10)

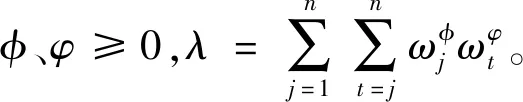
(7)对各个备选方案的综合评价值rk由大到小进行排序，得到最优方案。

4 案例分析与比较

4.1 实例分析

某公司为宣扬公司文化，决定建立一个带有其特色文化的小镇，笔者将基于IVqOFWHCS测度的多属性群决策方法，解决该公司建立特色文化基地的选址问题，以考量基于IVqOFWHCS测度的多属性群决策方法的合理性和实用性。已知4个选址的备选方案集F={F1,F2,F3,F4}，属性集U={U1,U2,U3}，即从地理位置(U1)、文化氛围(U2)、交通便利程度(U3)3个方面对选址进行考量，并假设q=3。

(1)3位决策者Dj(j=1,2,3)在每个属性下对4个选址方案进行评价，以[0,1]区间形式给出方案的满意度和不满意度，从而构成了3个评价矩阵A(1),A(2),A(3)，分别如表1～表3所示。

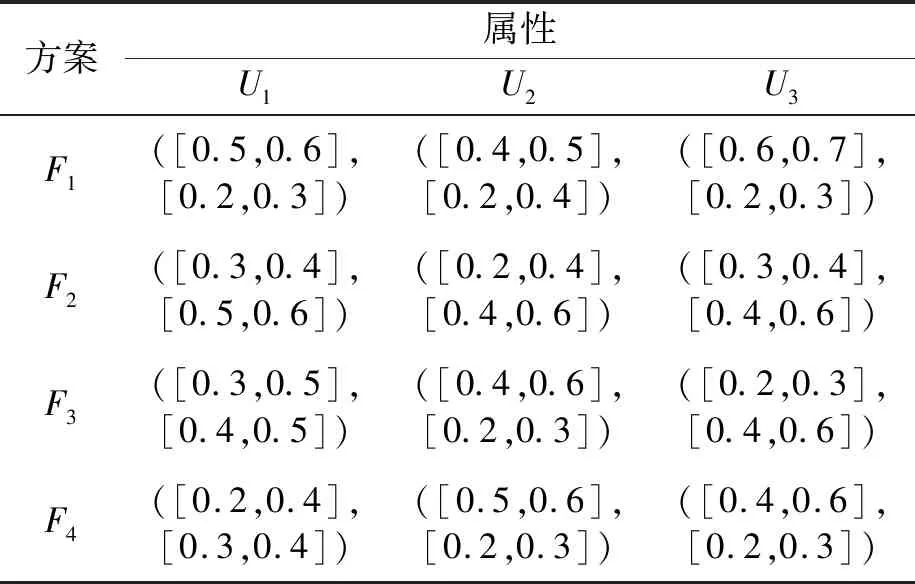
表1 决策者D1给出的评价矩阵A(1)

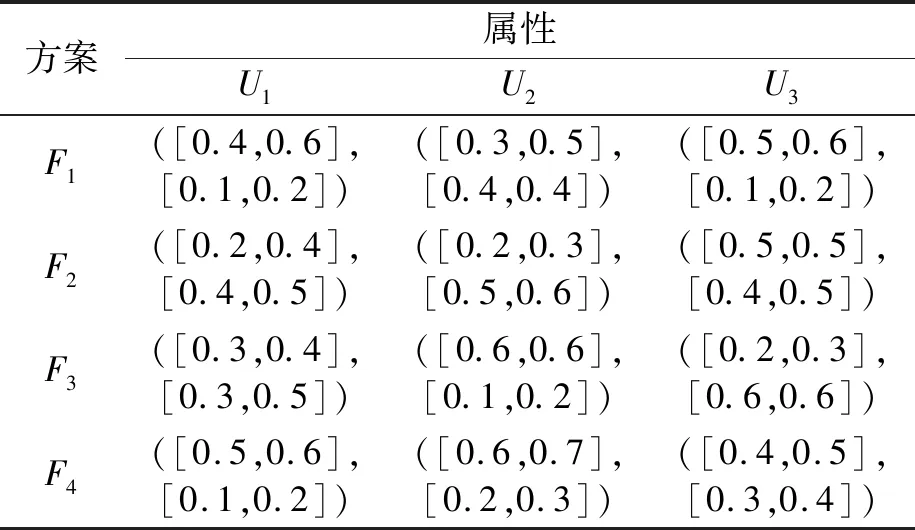
表2 决策者D2给出的评价矩阵A(2)

表3 决策者D3给出的评价矩阵A(3)

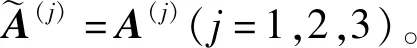
(3)利用式(8)计算评价矩阵中每个评价值的得分值，得到每个决策者评价值的得分矩阵S(1),S(2),S(3),分别如表4～表6所示。

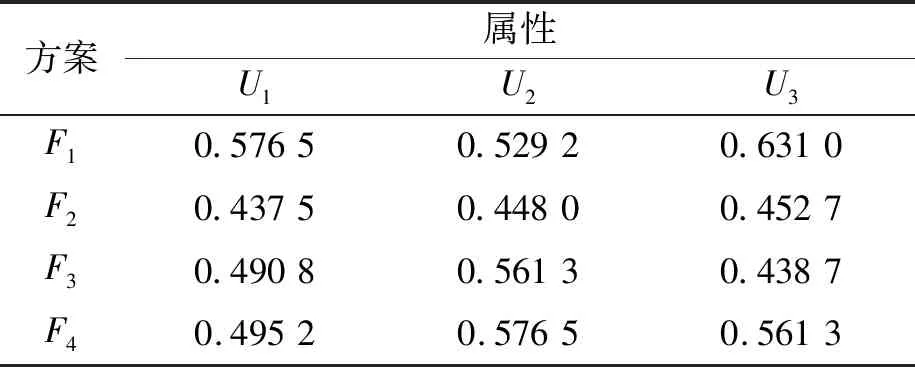
表4 决策者D1评价值的得分矩阵S(1)

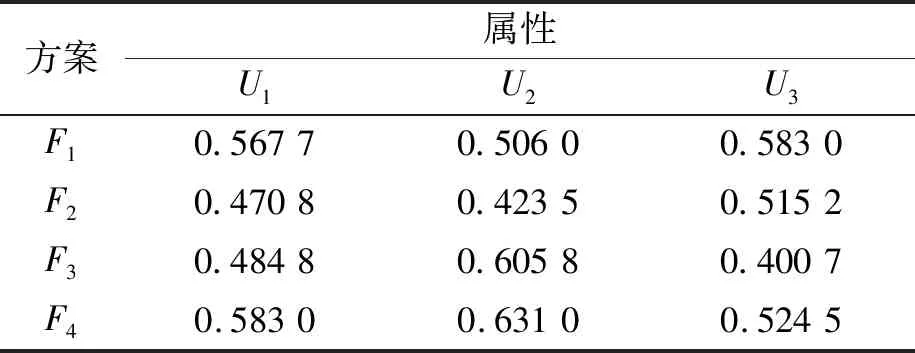
表5 决策者D2评价值得的分矩阵S(2)

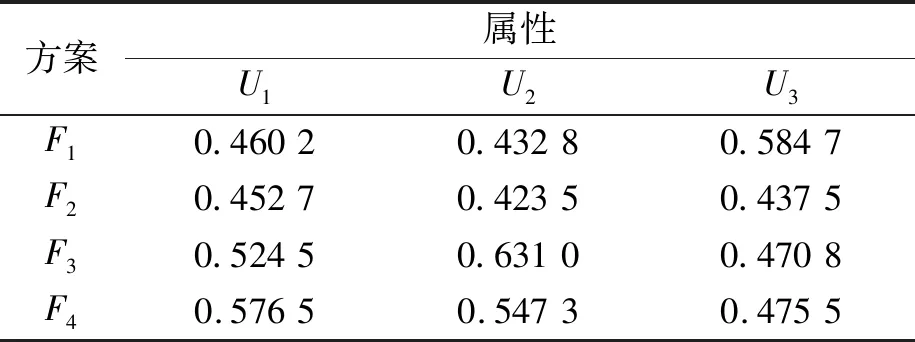
表6 决策者D3评价值的得分矩阵S(3)

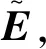
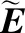
表7 决策者的理想评价矩阵

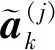
(6)设决策者的权重为ω1=0.3,ω2=0.4,ω3=0.3，利用IVqOFWHCS测度集结加权余弦相似测度。并设φ=φ=1/3，得到各备选方案Fk的综合评价值rk，即r1=0.273 1,r2=0.082 4,r3=0.207 4,r4=0.314 3。

(7)对各个备选方案的综合评价值从大到小进行排序，得到r4>r1>r3>r2，故最优方案为F4，该公司应按照方案F4为特色文化基地选址。

4.2 灵敏度分析

为了分析参数q、φ、φ对决策结果的影响，笔者进行参数的灵敏度分析。通过固定和更改参数值，考量参数值的变动对该案例中最优备选方案决策的影响。

(1)当φ、φ值不变时，考察q值变化对综合评价值的影响。令φ=φ=1/3，利用Matlab编程并绘制不同q值下方案综合评价值的变化图,如图1所示。从图1可以看出，随着q值的逐渐增大，方案的综合评价值逐渐减小并趋近一个定值，备选方案F4的综合评价值始终高于其他方案，始终为最优方案。

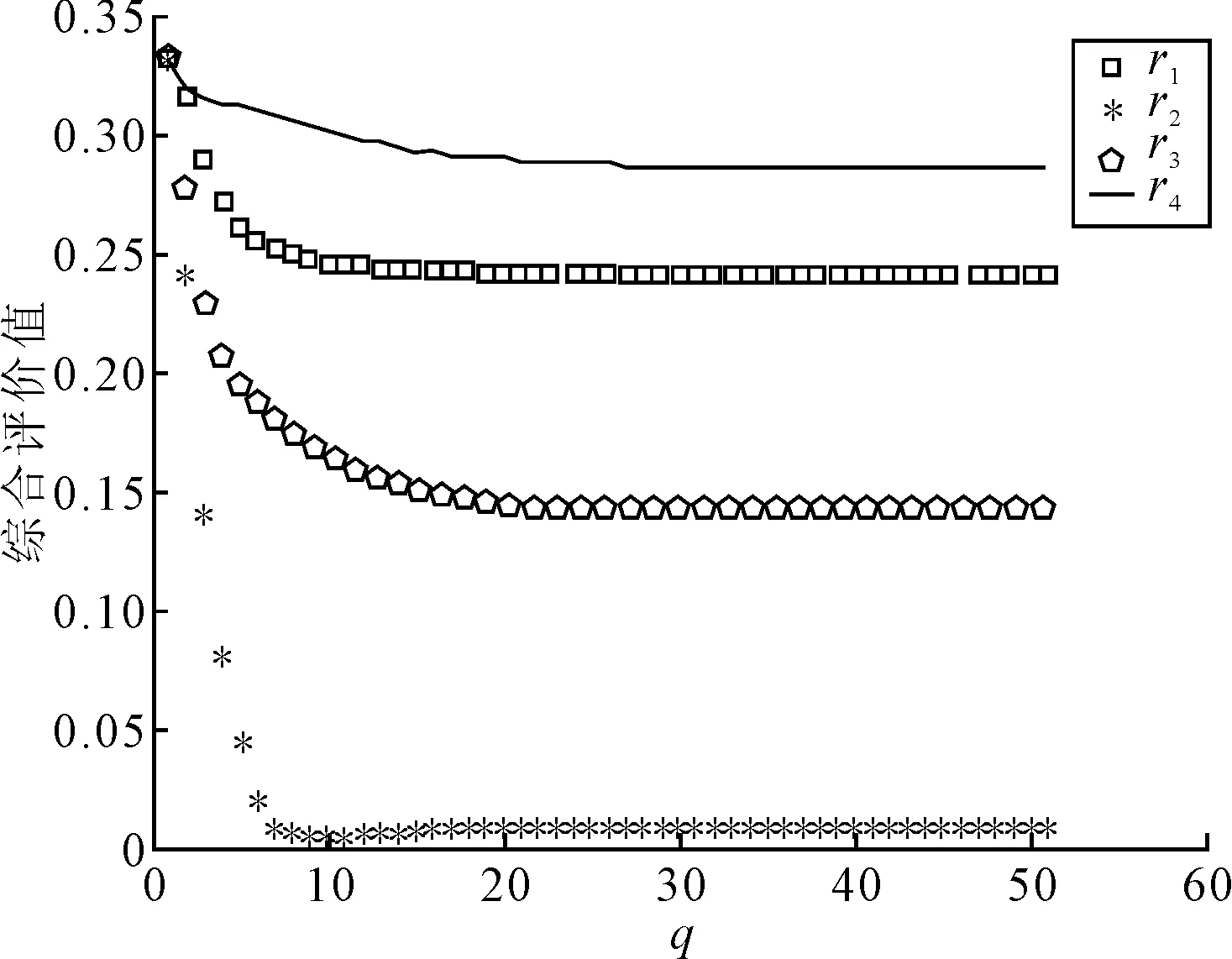
图1 不同q值下方案综合评价值的变化图

(2)当q值不变时，考察φ、φ值变化对综合评价值的影响。令q=3,利用Matlab编程并绘制不同φ、φ下各方案综合评价值的变化图，如图2所示。从图2可以看出，随着参数值φ、φ的不断变大，方案的综合评价值不断增大，但最终评价值均趋于稳定。

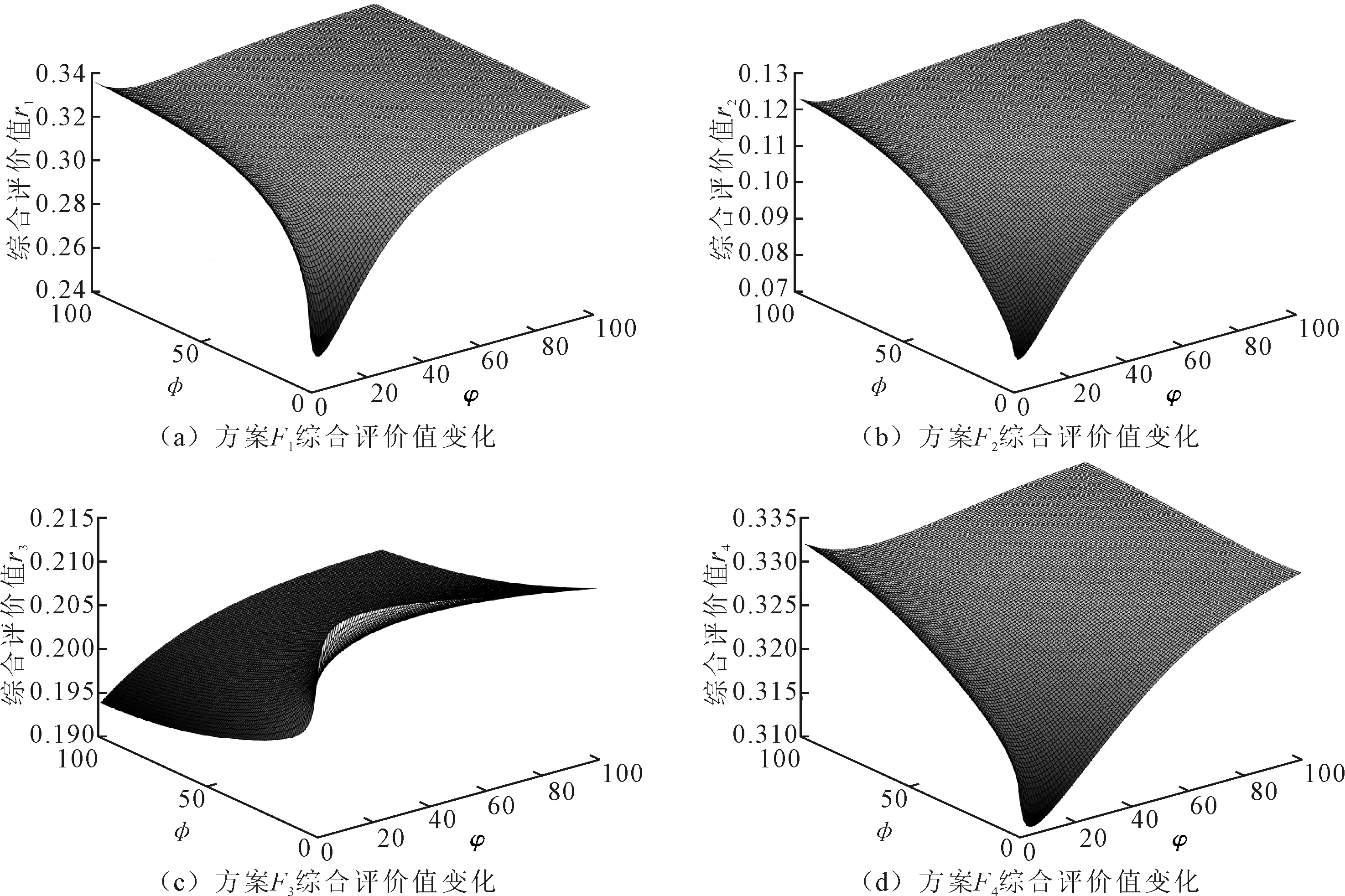
图2 不同φ、φ下各方案综合评价值的变化图

(3)当q、φ、φ值同时变动时，选取部分参数值代入Matlab程序中进行计算，得到不同q、φ、φ值下综合评价值的变化情况，如表8所示。从表8可以看出，备选方案F4的综合评价值仍然显著高于其他方案，方案的排序没有变动。

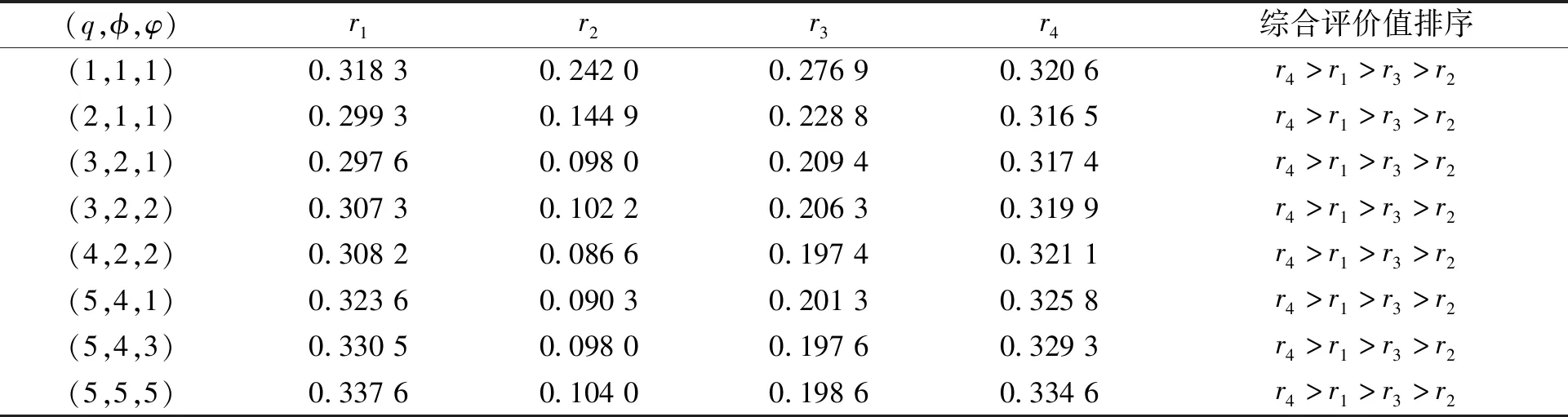
表8 不同q、φ、φ值下综合评价值的变化情况

由上述结果可知，参数φ、φ的变动会对方案的综合评价值造成影响。当φ、φ取值较大时属性之间关联性较强，此时φ、φ取值对信息集成的结果影响不大，故方案排序趋于稳定。参数q值的变动也会对结果造成影响，但随着q值的增大，方案的排序也是趋于稳定的。在解决实际问题时，决策者应适当选取参数，但不建议选用过大或过小的参数。

4.3 比较分析

(1)将文献[14]～文献[16]中的算子应用于上述案例中，计算各方案的综合评价值并进行排序，得到的结果如表9所示。通过结果的对比分析可知，IVqOFWHCS测度、IPFOWCS测度、q-RIVOFWMSM测度和q-RIVOFWHM测度选出的最优方案均为F4,而q-RIVOFWDMSM测度和q-RIVOFDHM测度选出的最优方案为F1。不同的算子采用了不同的集结方法，但计算出F1和F4两方案的综合评价值十分接近，皆可称为最优备选方案。

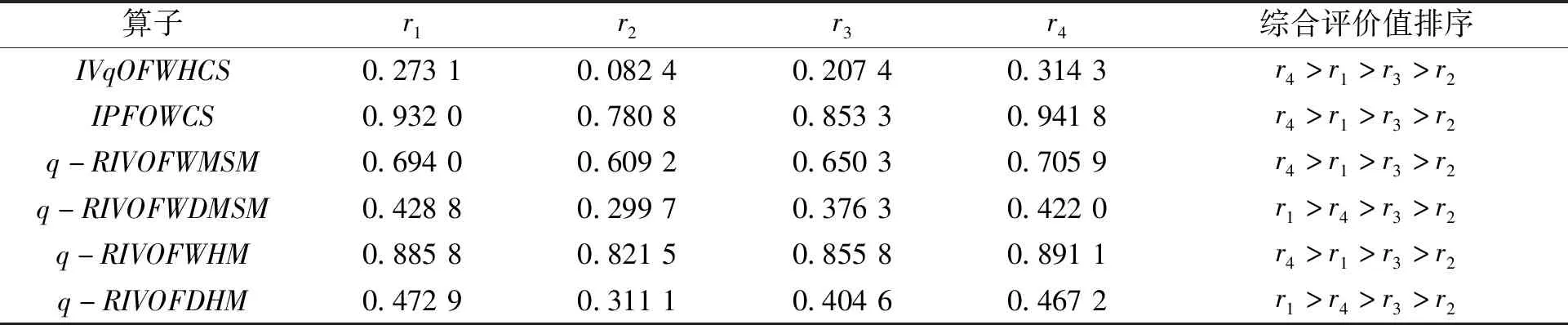
表9 不同算子下各方案的综合评价值及排序

在决策过程中通常假设属性之间是相互独立的，如文献[12]中所运用的OWA算子。但实际中属性之间可能存在关系，故由此对最优方案的决策并不准确。而笔者所提出的广义Heronian平均算子充分考虑了属性之间的相互作用，决策者可以根据偏好，主观输入参数值，得到最优方案。文献[15]和文献[16]所使用的算子均考虑了属性之间的相互作用，得出的结果与IVqOFWHCS测度计算出的结果一致，验证了笔者所提出的基于IVqOFWHCS测度的多属性群决策方法的有效性。

(2)将IVqOFWHCS测度与文献[17]中VIKOR法的结果进行比较。不同参数值时VIKOR法得到的最优方案集合有{F2,F3,F4},{F1,F3,F4},F4，而IVqOFWHCS测度下最优方案为F4，两种方法得到的结果略有不同，造成差异的原因是这两种方法对问题进行决策的侧重点不同。两者均考虑了属性之间关联程度对决策的影响，但在考虑模糊测度问题时，VIKOR法利用理想解概念对决策者的评价值进行筛选，并由此计算属性权重和方案评价值，在计算上略显繁琐。而IVqOFWHCS测度利用加权余弦相似测度来刻画两个向量之间的模糊测度，具有直观的几何意义，原始信息利用率高，减小了信息损失。利用广义Heronian平均算子对模糊测度进行集结，参数取值灵活使得能够较全面地考虑实际问题，这也是笔者所提出方法的先进之处。

5 结论

在区间Orthopair模糊环境下，研究了一种基于区间Orthopair模糊Heronian测度的多属性群决策方法。该方法利用加权余弦相似测度刻画模糊向量间测度，减少了信息损失，并基于广义Heronian平均算子对相似测度进行集结，考虑了属性间关联程度对于决策的影响。通过实证分析和不同测度方法的对比分析，验证了该方法的有效性和先进性。