考虑人员流动的邮轮空间传染病模型研究

房志明，徐韵如，黄芳旧，黄中意，李晓恋，庄 磊，陈国庆，宋卫国

(1.上海理工大学 管理学院，上海 200093；2.上海海事大学 海洋科学与工程学院，上海 201306；3.中国船级社上海规范研究所，上海 200135；4.中国科学技术大学 火灾科学国家重点实验室，安徽 合肥 230026)

截止到2020年7月24日，全球新型冠状病毒肺炎确诊病例超1 500万人，造成超过63万人员死亡。而且，目前国外的疫情控制仍不乐观，感染人数与伤亡人数仍保持上升趋势。在疫情的发生发展过程中，某些大型邮轮上的疫情发展与应急处置一直备受瞩目，例如“钻石公主”号邮轮最终确诊712例(总人数为3 711人，感染比例为0.191 9)；“至尊公主”号邮轮确诊至少103例；“红宝石公主”号邮轮确诊超600例。

对于重大传染病疫情，一方面，邮轮本身是一种交通工具，会加快病毒在地域之间的传播；另一方面，邮轮上的人员长时间处于相对封闭的环境中，增加了相互传播感染的风险。因此，科学、有效的邮轮传染病防控措施成为迫切的现实需求，这就需要了解邮轮内病毒传播机理，分析邮轮内病毒传播过程。

从系统科学的角度来看，传染病是在人群中发生的一个复杂的扩散过程，针对这一过程建立模型，有助于理解传染病的流行机理，认识内在规律[1]。目前传染病传播模型主要包括3种，分别为单一群体模型(将人群看作一个整体)、复合群体模型(考虑人群在空间的异质性，将人群划分为多个子群体)和微观个体模型(制定个体的属性和行为规则，形成网络上的传播动力学过程)[2-3]。

单一群体模型将人群看作一个整体，用偏微分方程描述健康人群、感染人群、恢复人群、死亡人群之间的转换关系。如KERMACK等[4]在1927年提出的SIR模型是一种经典的单一群体模型，该模型将人群划分为易感者、感染者、移除者和健康者，并引入平均接触人数，指出平均接触人数是影响传染病传播的关键因素；蔡全才等[5]在SIR模型的基础上建立了SEIRP模型，引入并分析了接种和隔离的影响；HOPPENSTEADT[6]提出考虑年龄结构的传染病模型，刻画了年龄异质性对传染病的影响。

复合群体模型将人群按照定义明确的社会单元划分成不同的子群体，借助图论的相关理论研究不同地区之间由于人员移动导致的传染病现象。如CROSS等[7]建立了11×11的方格模型，每个方格内的子群内部采用SIRS模型，子群中的个体可以移动到相邻子群；COLLIZZA等[8]用SIR模型描述子群内部的流动，用网络描述子群之间的链接方式，得到流行病传染的门槛条件；WATTS等[9]将人群看作多层级结构，建立复合群体模型，讨论层级对传染病流行的影响；倪顺江[10]提出交替社会网络模型，并指出传染病在家庭网络中的传播速度明显低于公共网络。

微观个体模型则通过制定个体的属性和行为规则，利用个体之间形成的接触网络模拟传染病的发展过程。KLECZKOWSKI等[11]将元胞自动机应用于传染病流行过程的模拟中，并讨论了人员流动和及时就医对疫情传播的影响；EUBANK等[12]开发了EpiSimS，基于调查数据建立了大城市的人际接触模型，并研究了天花在城市的传播与控制；MILNE等[13]根据澳大利亚一个城镇的人口、家庭特征和场所设置信息建立了虚拟网络模型，描述人员的接触、感染过程，并研究了防控措施对流感的干预效果；徐展凯等[14]以社会接触网络为载体，以个体为单位建立基于个体的传染病传播模型，并基于该模型讨论了个体行为变化在传染病传播过程中发挥的作用。陈长坤等[15]基于元胞自动机方法，根据区域特性将区域划分为静态区域和动态区域，同时考虑了区域内传染病传播和区域间人口迁移的过程，建立了具有移动性和人口迁移功能的SIR传染病跨区域传播模型，分析了动态区域位置与面积对传染病跨区域传播的影响规律。

针对传染病传播过程，目前已在宏观(单一群体模型)、微观(微观个体模型)和介观(复合群体模型)层面上建立起较为完备的模型体系，但针对某些重点区域内部，特别是具有相对封闭特性的邮轮内传染病传播模型与防控措施的研究还较为稀缺。因此，笔者建立了一种耦合人员流动与病毒近距离接触传播的传染病传播模型，分析邮轮上人员活动引起的病毒近距离接触传播过程，以探索邮轮的重大传染病疫情防控措施。

1 模型

1.1 邮轮人员流动模型

邮轮人员流动模型的主要规则如下：

(1)根据邮轮平面图定义邮轮上全体乘客和船员的活动模式，包括去餐厅(一日三餐)，去休闲区(酒吧、甲板等，随机发生)，返回房间(白天随机发生，夜晚回房休息)等。

(2)在规定的活动模式下给每个模拟人员随机赋予“时间-活动”序列，如给一个模拟人员X赋予如下“时间-活动”序列：“7:06-去餐厅”，“9:23-去休闲区”，…，“21:34-返回房间”。

(3)对于每个模拟人员，当到达了“时间-活动”序列中的某个时间时，相应的活动模式就被执行。例如对于模拟人员X，当时间到达7:06时，便开始运动。

(4)模拟人员的运动规则与人员疏散模型中的规则一致[16]，只是疏散模型中人员的目的地是安全出口，而邮轮人员流动模型中人员的目的地是餐厅、休闲区、房间等。

1.2 基于人员流动模拟的病毒传播模型

基于邮轮人员流动模型，引入病毒近距离传播规则，建立基于人员流动模拟的病毒传播模型。其中，病毒近距离传播规则如下：

(1)定义d表示病毒的有效传播距离，Rper表示人员感染病毒的概率。

(2)在人员流动过程中，随着相互之间的密切接触，人员感染病毒的概率由式(1)确定。

(1)

对于新型冠状病毒，根据目前公开的新闻报道和统计数据，式(1)中参数的设定为：①β=0.02，d=1 m；②在一定范围内，接触时间Δt越长，病毒传染性越大，定义f(Δt)=min(Δt/tcon,1)，其中tcon表示确定形成一次病毒传播的接触时间，文中取tcon=4 min；③新型冠状病毒在潜伏期内也具有传染性，假设潜伏期内该病毒的传染性逐渐增强，定义f(nday)=min(nday/Iper,1)，其中Iper表示病毒潜伏期天数，文中取Iper=7。

(3)模型中可设置一个或多个初始病毒携带者，初始病毒携带者Rper=1。

(4)定义Nperson、Pprotect分别表示邮轮上总模拟人数和采取防护措施的人员比例，则邮轮上有Nperson·Pprotect个人员采用防护措施。假设人员采用防护措施的保护效果等同于N90口罩，那么若采用了防护措施，则式(1)中Sper=0.9，否则Sper=0。

(5)定义Ntravel代表邮轮的航行天数，即模型模拟的邮轮上人员活动与病毒传播天数。当模拟计算完成时，则最终整体病毒感染率Rcrowd为：

(2)

2 模拟与分析

2.1 模拟对象

建模实例原型为网络上一个公开的邮轮平面图(维诗达邮轮公司的总统六号邮轮)，如图1所示(图片来源为http://www.vst88.com/Youlun/ChuanZhiCJ.aspx?id=97cd8b90-77fd-4deb-bda8-bb1a681ddeae)。该邮轮共有5层公共甲板，157间客房，3间餐厅，7个休闲区域(阅览室、酒吧、阳光甲板、吸烟区等)。

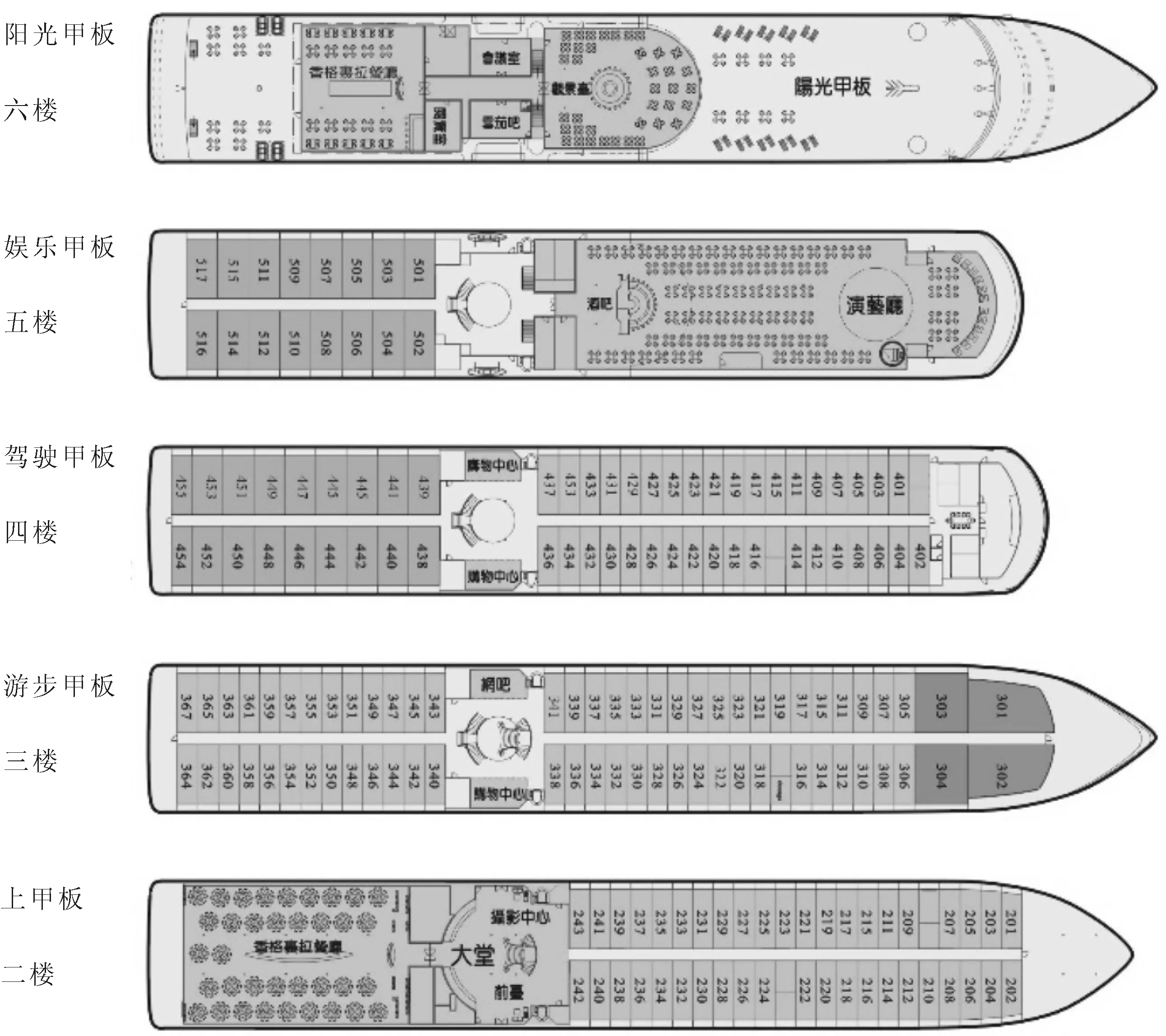
图1 邮轮平面布置图

建立邮轮的人员流动与病毒传播模型，如图2所示。假设每个房间有2名人员，则游轮上总模拟人数Nperon=354。

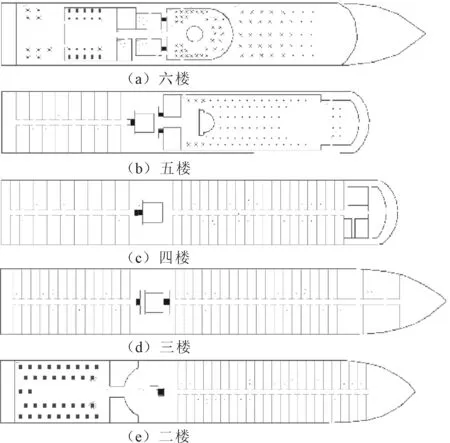
图2 邮轮的人员流动与病毒传播模型

2.2 基础场景

模拟邮轮航行期间，邮轮上人员正常活动下的病毒传播过程。为了与“钻石公主”号邮轮进行对比，模型中的航程设置与“钻石公主”号一致。首先，需要回顾新型冠状病毒肺炎疫情发展与“钻石公主”号的关键时间点：1月20日，“钻石公主”号邮轮从日本横滨出发；1月23日，武汉开始封城；1月25日，“钻石公主”号邮轮上一名80岁的乘客在香港下船，随后出现发烧症状；2月1日，香港下船的乘客被确认感染新型冠状病毒；2月3日，“钻石公主”号邮轮返回横滨港。

参考“钻石公主”号邮轮的实际行程，定义模拟基础场景：邮轮上存在一名初始病毒携带者，邮轮行程期内病毒在人群中传播发展。基础场景的关键参数为：①“钻石公主”号邮轮行程大约为14天，模型中设置Ntravel=14。②调整邮轮上采取防护措施的人员比例Pprotect，计算人群中采用防护措施的人员数量不同时病毒感染情况。③每个Pprotect值对应的场景计算5次，求平均值，得到基础场景下不同防护比例Pprotect时病毒感染率情况，如图3所示。

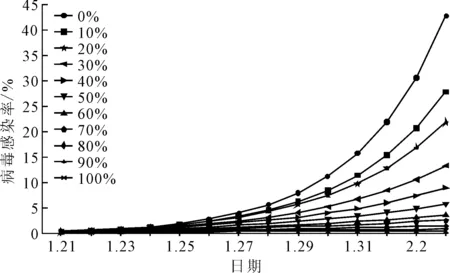
图3 基础场景下不同防护比例Pprotect时病毒感染率

从图3可以看出，在没有个体防护情况下，整体的病毒感染率Rcrowd将达到42.9%。随着采取防护措施的人员比例Pprotect的增加，Rcrowd显著下降，当有一半人采取防护措施时，Rcrowd可降低到5.8%；如果做到完全防护(Pprotect=100%)，Rcrowd可以降低到0.5%。

2.3 防护场景

在“钻石公主”号航行期间，乘客和船员并没有采取较好的防护措施。如果人群处于完全无防护状态下，模拟预测病毒感染率会达到42.9%，远远超出了“钻石公主”号实际感染率。原因有两点：一是“钻石公主”号初始病毒携带者中途下船；二是根据一些报道，有些乘客在登船之初准备了口罩，而且在1月23日武汉封城消息到达后，部分乘客开始逐渐加强自身防护。因此，笔者设计了防护场景，用以模拟疫情警示信息到达后，人们主动或者在管控措施下提升自身防护水平的情况。

与基础场景相比，防护场景的不同之处在于：①Pprotect初值为0；②从1月24日开始，Pprotect提高并保持在一个较高的值，分别为10%，20%，…，100%，作为对比，设置了Pprotect始终为0的场景，如表1所示；③初始病毒携带者及其房间同住人员于1月25日下船(1月26日，这两名人员的Pper重新设置为0)；④每个防护场景均计算5次，求平均值。

表1 防护场景参数设置

防护场景下的病毒感染率变化曲线如图4所示，每种防护场景下的病毒感染率及换算(按总人数为3 711人换算)“钻石公主”号病毒感染人数如表2所示。结合图3和图4，对比基础场景和防护场景下Pprotect= 0时的曲线，可知初始病毒携带者中途下船使病毒感染人数大幅下降，因此需要在模拟分析时考虑初始病毒携带者中途下船的影响。综合“钻石公主”号上人员状况的有关报道，防护场景1比较符合“钻石公主”号病毒发展与人群防护状态的实际情况，即在接收到足够疫情信息尤其是武汉封城信息后，邮轮上很少一部分人(10%左右)会自主加强个人防护，包括佩戴口罩，避免近距离接触等。场景1的最终病毒感染率为0.182 6±0.021 7，换算成“钻石公主”号的病毒感染人数为677.77±80.68，与实际情况(感染率为0.191 9，712人)一致。一方面，证明了笔者所构建的模型可用以模拟邮轮内人员活动与病毒传播的耦合过程；另一方面，笔者是对航程期间病毒传播过程的预测，预测结果与最终确诊病例一致，说明“钻石公主”号邮轮实际的病毒传播大都发生在航程期间，而在隔离期间并没有造成大规模的感染。

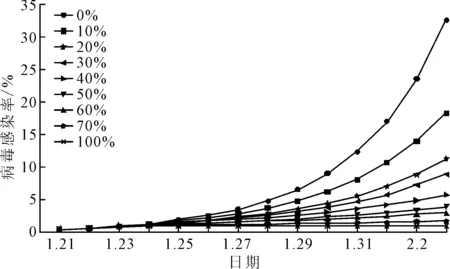
图4 防护场景下的病毒感染率

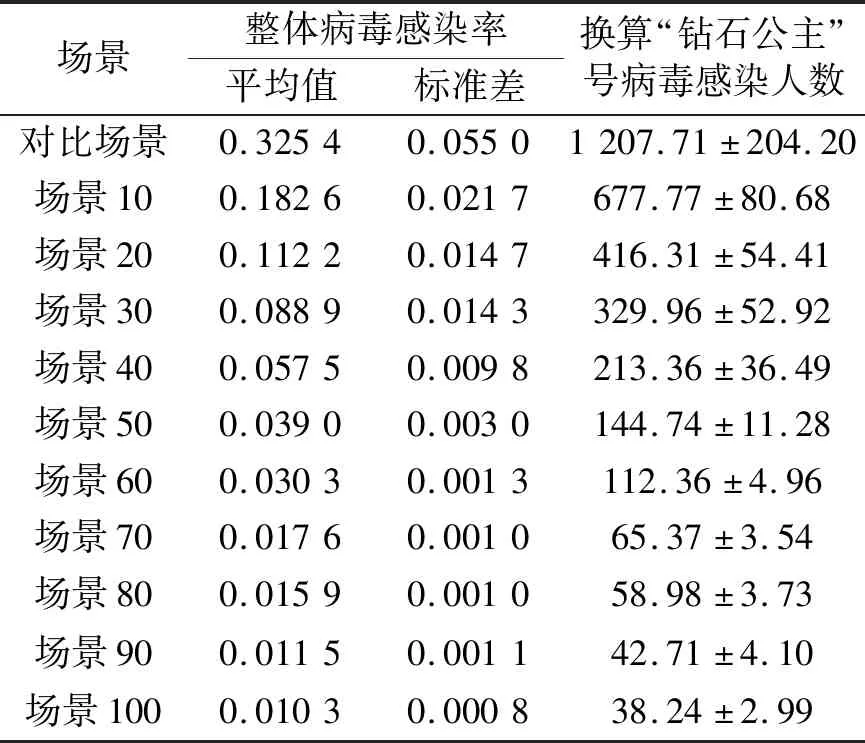
表2 防护场景的模拟结果

从表2还可以看出，当邮轮管理方收到疫情警示信号(如武汉开始封城)后，如果能够及时采取提醒或强制性措施，让邮轮上的人群加强个人防护，就能显著降低病毒感染率。如果人员防护比例增加到50%，就能将感染人数降低到144.74±11.28；如果能实现完全防护，就能将感染人数降低到38.24±2.99。同时，通过对比模拟结果与实际情况，也证明了“钻石公主”号管理方未采取合理的防控措施。

3 结论

(1)通过建立耦合人员流动与病毒近距离接触传播的传染病传播模型，模拟分析了不同场景下，邮轮在航行过程中由人员日常活动中密切接触造成的病毒传播情况。

(2)建立了基础场景模拟邮轮中采取防护措施的人员数量不同时病毒的传播情况，结果表明在邮轮这种有限密集人群空间内，如果没有采取个体防护措施，在14 d的行程时间内，邮轮人群病毒感染率将会超过40%。

(3)建立了防护场景模拟在疫情信息驱动下，人们主动或者在管控措施下提升自身防护水平的情况。并设计了一种与“钻石公主”号邮轮实际情况比较相符的场景，该场景模拟“钻石公主”号的最终确诊病例数为677.77±80.68，与实际最终确诊人数一致，说明所构建的模型可用于模拟邮轮内人员活动与病毒传播耦合过程，且邮轮隔离期间并没有造成大规模的感染。

(4)防护场景模拟结果表明，如果在疫情警示阶段，管理者能够立即采取有效的提醒与管控措施，即使仅采用“让人们加强个人防护水平”这一措施，即可有效降低邮轮的感染人数。而实际确诊数据则表明“钻石公主”号邮轮管理者并没有采取适当的管控措施。