禁忌搜索算法下求解TTRP的邻域算子研究

2020-09-23边星驰

武汉理工大学学报（信息与管理工程版） 2020年4期

边星驰

(武汉理工大学物流工程学院，湖北武汉 430063)

甩挂运输是指使用卡车牵引挂车完成货物运输，并在指定地点进行挂车的卸挂、拖带等操作的一种货物运输方式。在甩挂运输方式下，卡车可与挂车分离，这样的协同方式使货物的装卸和运输过程并行，简化了货物的装卸作业环节，缩短了卡车和司机的等待时间，提高了车辆和司机的利用率[1]。在欧美等发达国家，甩挂运输发展较为成熟，其在社会总运输量中的占比达70%～80%[2]。受限于各种因素的影响，我国的甩挂运输起步较晚，但近年来以较快的速度发展。2010年10月，国家发改委和交通运输部制订了《甩挂运输试点工作实施方案》。在“十二五”期间交通运输部在全国组织实施209个甩挂运输试点项目，累计拉动社会投资约278.6亿元，为全社会节省燃油约21万t，节约物流成本近300亿元。2016年交通运输部制订了《综合运输服务“十三五”发展规划》，提出要推动甩挂运输方式在我国的全面发展。因此，研究甩挂运输对推动物流运输走向集约化发展，提高运输系统运行质量和社会资源利用率等都具有重要的现实意义。

甩挂运输路径规划问题(truck and trailer routing problem，TTRP)是传统车辆路径问题(VRP)的衍生问题，与VRP相比，TTRP中车辆和客户均为异质，使网络中的路径类型更为复杂，研究难度增加。TTRP的求解方法主要包括精确式算法和元启发式算法两类。

在甩挂运输路径规划问题研究方面，BELENGUER等[3]提出利用整数规划模型来解决单卡车的TTRP，并设计了几种不同的卡车和挂车的分离方式，最后使用分支定价算法对该问题进行了求解。DREXL[4]提出了一种分支定价算法并用于求解GTTRP(generalized truck and trailer routing problem)，该算法基于动态规划的标号算法实现。ROTHENBCHER等[5]针对带时间窗的TTRP提出一种分支-价格-切割，并且使用该算法解决了两个实际场景下的甩挂运输路径规划问题。

受限于求解规模和灵活度，在求解TTRP时，精确式算法的使用和相关研究不及启发式算法广泛深入。在启发式算法中，学者大多采用元启发式算法，该算法可行解的质量比一般启发式算法更优，具体包括禁忌搜索算法、模拟退火算法和变邻域搜索算法等。

CHAO[6]最早提出标准TTRP的概念，构造了21个通用的TTRP测试算例，并设计了基于禁忌搜索的算法框架。SCHEUERER[7]利用禁忌搜索算法求解标准TTRP，并在路径构建阶段设计了T-Sweep和T-Cluster算法，提升了构建阶段的求解质量。LIN等[8]首次采用了基于模拟退火的算法来求解TTRP，在文献[6]构造的21个测试数据集中更新了11个当前最好解。王超等[9]设计了一种基于迭代变邻域的下降算法(iterated variable neighborhood descent，IVND)来求解TTRP，在保证求解质量的同时，大幅缩减了算法的求解时间。郝友文等[10]对遗传算子在VRP中的应用做了相关综述，并按照选择算子、交叉算子、变异算子3种算子类型展开描述。

综上可知，现有针对TTRP的研究主要集中在算法的求解质量和运行性能上，缺乏关于邻域算子与求解结果的关系分析。为了探究邻域算子与实验结果的影响机制，笔者针对邻域算子与元启发式算法求解结果的影响关系，设计了基于禁忌搜索的两阶段算法来求解TTRP，最终通过对比实验来探究邻域算子与求解质量的关系。

1 问题描述

标准TTRP模型的描述如下：有多辆卡车和多辆挂车，从中心仓库出发，对需求和位置都已知的客户进行服务。卡车数和挂车数已知，挂车可以和任意卡车组合，组合后的车辆称为完备车辆。由于道路宽度、法律法规等客观条件的限制，客户分为TCs客户(truck customers)和VCs客户(vehicle customers)两类，前者只能单独由卡车进行服务，后者既可单独由卡车进行服务，也可由完整甩挂车进行服务。网络模型可表示为G=(V,A)，其中V={0,1,2,…，n}为客户点集合。由于存在两类车辆和两类客户，故TTRP可以抽象出3种类型的路径，3种路径的示意如图1所示。其中，纯卡车路径(PTR)可以服务TCs和VCs；完备车辆路径(PVR)没有子回路；带子路的完备车辆路径(CVR)，由一个甩挂运输车路径作为主路径和若干纯卡车路径的子路径组成。

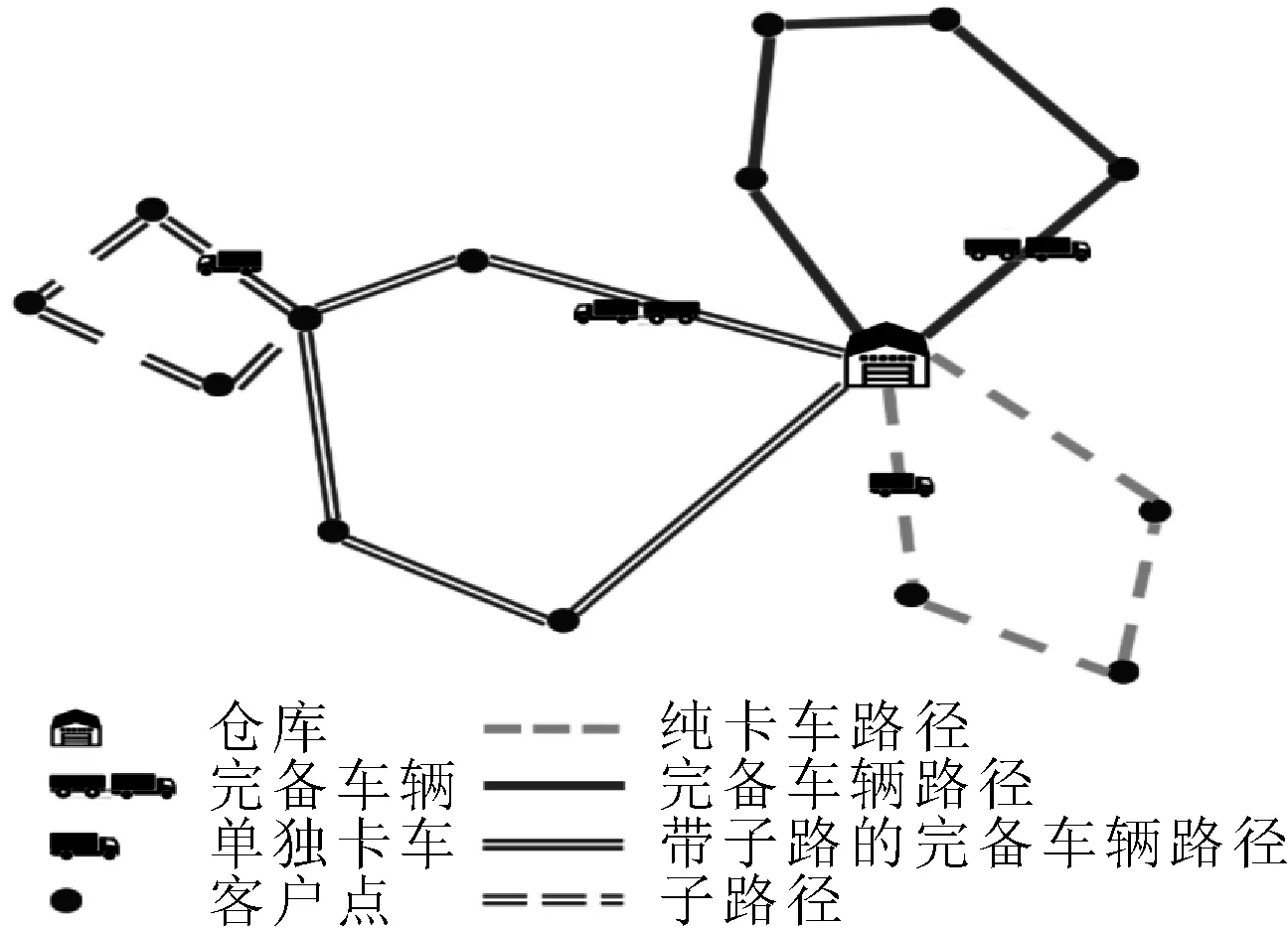
图1 TTRP的3种路径示意图

2 算法设计

2.1 算法框架

笔者采用两阶段算法，即在第一阶段使用CPLEX和下降改进算法得出问题的初始解，然后使用禁忌搜索算法改进初始解。为了扩大邻域搜索范围，在下降改进阶段和禁忌搜索阶段使用3种不同的邻域算子。CPLEX通过求解松弛的指派问题将每个客户分配到某一类路径上，禁忌搜索算法同时设置了基于历史移动的禁忌规则和基于目标函数的禁忌规则，以避免搜索陷入局部最优，跳出当前邻域，实现搜索空间的分散化。

在算法的开始阶段先进行数据(数据来源于文献[6])的读取，数据读取结束后进行松弛指派问题的求解，求解完成后每位客户都会被分配至一条路径上，依此进行路径的构建。此时构建完成的路径可能存在超载的情况，需要将路径进行初步优化，使不可行解转化为可行解。该阶段使用下降改进优化算法，当新的解具有更短的路径长度时，接受该解为当前最好解，直到不再出现新的更好解时，下降改进阶段结束，将输出解作为禁忌搜索阶段的输入。禁忌搜索又进一步分为集中搜索阶段和分化搜索阶段，以避免搜索陷入局部最优，当搜索满足最终停止条件时结束整个算法。

2.2 生成初始路径

初始路径的生成通过构造一个松弛指派问题来实现，模型的建立参照文献[6]。松弛指派问题经过CPLEX求解，路径中的每一个客户都完成了3种路径中某一种具体路径的分配，然后按照路径类型分别进行路径的构建：①对于PTR和PVR，直接使用最小花费插入算法进行路径构造。②由于CVR包含主路径和子回路，因此分两部分进行构造，主路径上的VCs利用TSP(旅行商问题)的最小花费插入算法生成路径。③对于子回路的生成，若已经有子回路，则将TCs插入到已有的子回路中。若还不存在子回路，则将TCs连接到主路的VCs上，生成一条新的子回路。

2.3 下降改进

下降改进是一种局部搜索算法，从初始值开始沿一定方向搜索领域内的解，直到到达该方向的最优解。若存在更好解，则会继续迭代；否则终止程序。下降改进算法和禁忌搜索算法的区别在于后者可以跳出局部最优解，而前者不能。

邻域解N(s)是指当前解s的所有可能邻解，通过对当前解s应用算子得到。实验中引入单点移动算子、双点交换算子和子路重构算子3类算子，并在下降改进结束后使用2-OPT进行路径内优化。

2.3.1 单点移动算子

单点移动算子是指在一个路径中选择一个客户点，移动到另一条路径中。在下降改进阶段，移动的条件是该次移动减少了超载量或没有增加路径长度，或者在没有增加超载量的前提下缩短了路径长度。有以下两类移动需要被排除：①将TCs移动到带子路的完备车辆路径的主路径上或者完备车辆路径上；②被移动的VCs是一个根节点即子路径的根节点，作为挂车卸挂点的客户点。

2.3.2 双点交换算子

双点交换算子是指选择两条路径，并在每个路径中选择一个客户点交换到另一条路径中。移动的条件是交换后的两条路径的超载量都没有增加，同时交换后的路径中有一条超载量减少或者交换的代价为负值(也就是交换后的目标值小于交换前的目标值)。此处排除的移动同上述单点移动算子。

2.3.3 子路重构算子

上述两个算子都没有进行子路径根节点的移动，而子路重构算子则是尝试改变一条子路径的根节点，以期缩短子路径的长度。具体过程为：保持子路径中客户点不变，改变子路径根节点的位置，即选择主路径中不同于最开始根节点的其他客户点作为新的根节点，如果新的子路径较之前的子路径长度有所缩减，则接受此次变换。子路重构的过程如图2所示，其中子路径的根节点由a变为c。

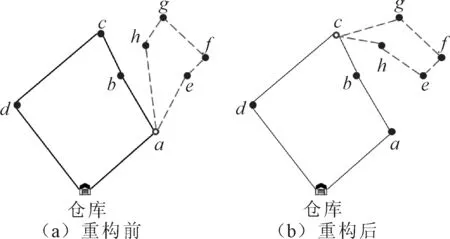
图2 子路重构示意图

2.4 禁忌搜索

2.4.1 集中搜索阶段

集中搜索阶段的主要目的是在当前搜索域进行更优解的搜索，此阶段设置松弛系数δ的初始值为0.01，递增步长λ为0.01，上限为0.10。下降改进阶段得到的初始解，是集中搜索阶段的输入。如果有新的更好解出现，则对新的路径实施下降改进优化，然后判断优化后的解是否达到程序结束条件，如果集中搜索阶段、分散搜索阶段和集中搜索后的下降改进总运行次数超过30次，并且有10次没有新的更好解产生，那么输出最终解。

2.4.2 分散搜索阶段

分散搜索阶段的主要目的是使搜索跳出当前的搜索域，以尝试找到当前搜索域之外的更好解，避免搜索过程陷入局部最优解的状态。此阶段设置松弛系数δ的初始值为0.10，递增步长λ为0.05。若出现新的可接受解，则结束该阶段的搜索。

2.4.3 禁忌规则

禁忌规则包括基于目标值(objective-based tabu restriction，OTB)和基于访问历史(frequency-based tabu restriction，FTB)两种。

OTB限定了禁忌搜索过程中解的值不一定要优于当前最好解，而是可以稍微大于当前最好解。这里设置的松弛系数在集中搜索阶段和分散搜索阶段分别以不同的初始值与步长递增。计算方式为：当前解的目标值-当前最好解的目标值<松弛系数×当前最好解的目标值。松弛系数递增的条件是当前搜索域中不存在新的可接受解出现。

FTB是指如果当前进行的移动，在禁忌表记录的长度内，就不再进行移动。禁忌表的长度随机设定，为6～10之间的某个整数，禁忌表内记录的内容包括当前移动的客户点i、目标移动路径的根节点k和目标路径的索引x，因为搜索过程中一旦发生移动，路径都会变化，所以需要用根节点k和索引x来共同确定当前移动的目标路径。

2.4.4 邻域算子

禁忌搜索部分的邻域算子和下降改进阶段的邻域算子类似，但也有差异，禁忌搜索部分采用单点移动算子和双点交换算子。

单点移动算子的移动条件较下降改进阶段有所变化，执行移动的判断条件为：①插入新客户点的路径超载量未增加；②原路径的超载量有所减少；③此次移动不触发OTB禁忌；④此次移动不触发FTB禁忌；⑤此次移动触发了FTB禁忌，移动后解为新的最好解，当候选移动满足条件①②④或①②⑤或①③④或①③⑤时，则执行该次移动为保证解的有效性，移动后的路径超载量不能大于0。双点交换算子和单点移动算子思路相同，需同时考虑两条参与交换的路径。

3 算例分析

3.1 测试环境及数据

计算机型号：华硕X550VC，CPU四核2.6 GHz，8 GB内存；操作系统：Windows10；Python版本：3.6.9；Cplex版本：12.80；代码运行环境：WSL(windows subsystem for linux)中的Ubuntu16.04。

为了研究算子不同的使用方式对结果的影响机制，使用3组测试数据，每组数据又包含2个算例。数据I：50个客户，1个中心仓库，5辆卡车，3辆挂车，卡车和挂车的运载量均为100。其中算例1中VCs和TCs的数量分别为38和12。算例2中VCs和TCs的数量分别为13和37。数据II：100个客户，1个中心仓库，8辆卡车，卡车运载量为150，4辆挂车，挂车运载量为100。其中算例3中VCs和TCs的数量分别为75和25，算例4中VCs和TCs的数量分别为25和75。数据III：199个客户，1个中心仓库，17辆卡车，卡车运载量为150，9辆挂车，挂车运载量为100。其中算例5中VCs和TCs的数量分别为150和49，算例6中VCs和TCs的数量分别为50和149。选择3组数据的依据是算例的规模，根据客户数可划分为小规模、中等规模和大规模3类。算例数据的概况如表1所示。

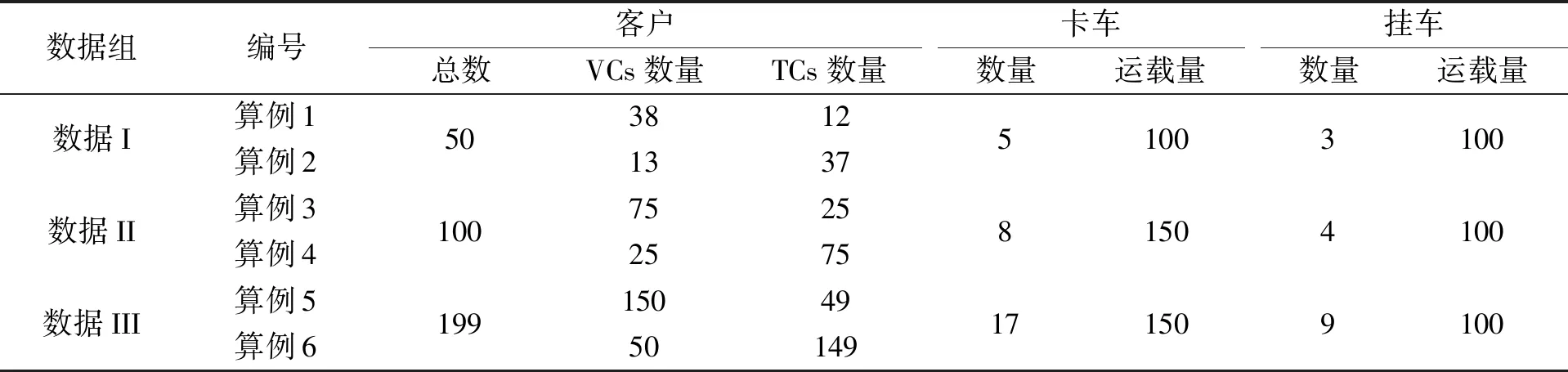
表1 算例数据概况

3.2 实验组别设置

组别A：下降改进阶段邻域算子设置相同，顺序执行。禁忌搜索阶段：①组A1x只使用单点移动算子；②组D0x使用单点移动算子和双点交换算子。

组别B：禁忌搜索阶段邻域算子设置相同，使用两类算子，顺序执行。下降改进阶段：①组B1x只使用单点移动算子；②组B2x使用单点移动算子和双点交换算子；③组D0x使用单点移动算子、双点交换算子和子路重构算子。

组别C：邻域算子的数目相同，下降改进阶段使用三类算子，禁忌搜索阶段使用两类算子。各组执行顺序：①组C1x下降改进阶段算子顺序执行，禁忌搜索阶段算子逆序执行；②组C2x下降改进阶段算子逆序执行，禁忌搜索阶段算子顺序执行；③组C3x下降改进阶段算子逆序执行，禁忌搜索阶段算子逆序执行；④组D0x下降改进阶段算子顺序执行，禁忌搜索阶段算子顺序执行。其中，x为算例编号，即1～6；组别D为其余3个组的对照组；下降改进阶段算子顺序执行为单点移动算子→双点交换算子→子路重构算子，反之为逆序执行；禁忌搜索阶段顺序执行为单点移动算子→双点交换算子，反之为逆序执行。数据I、数据II、数据III的实验结果分别如表2～表4所示。

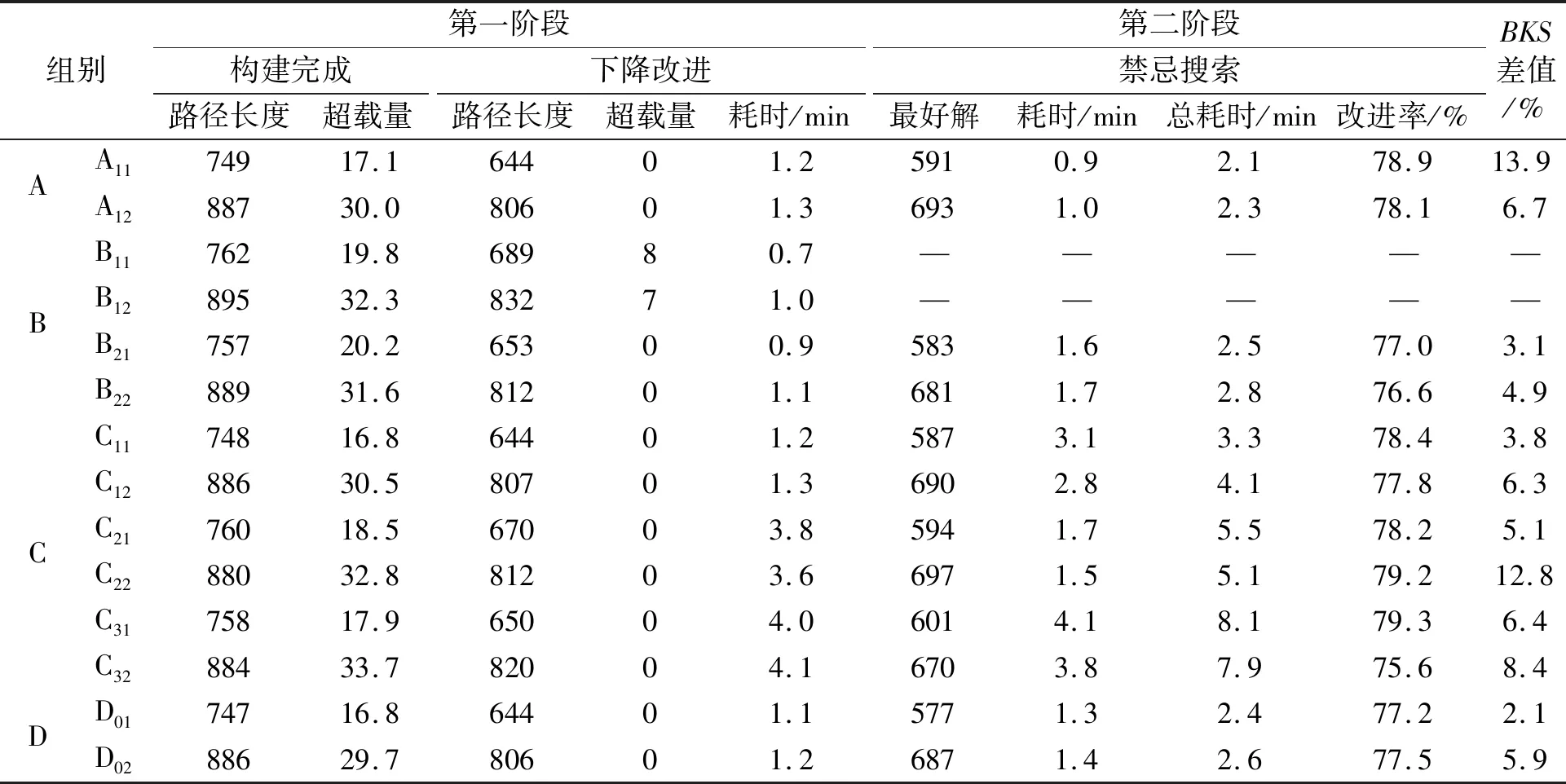
表2 数据I的实验结果

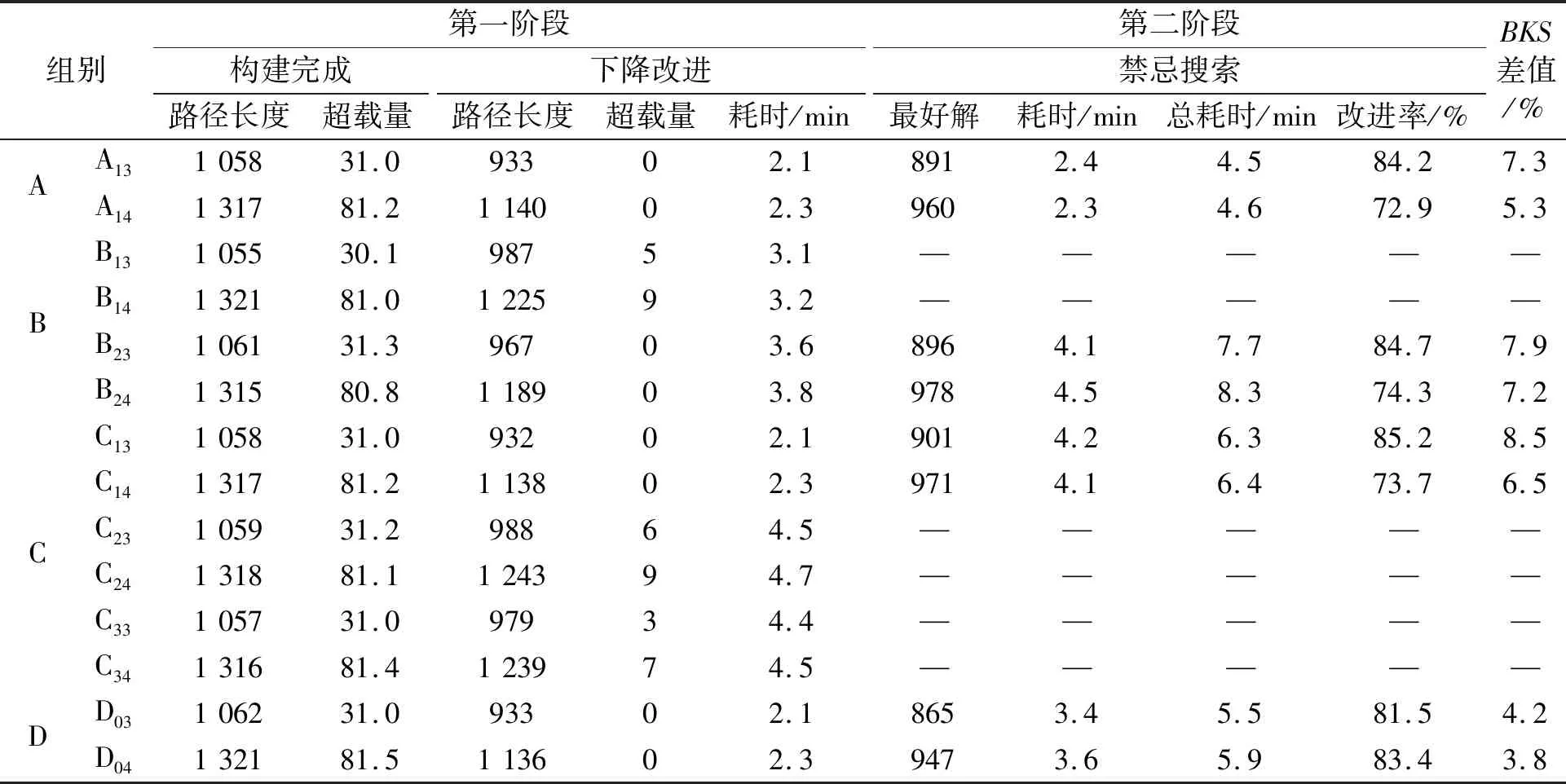
表3 数据II的实验结果

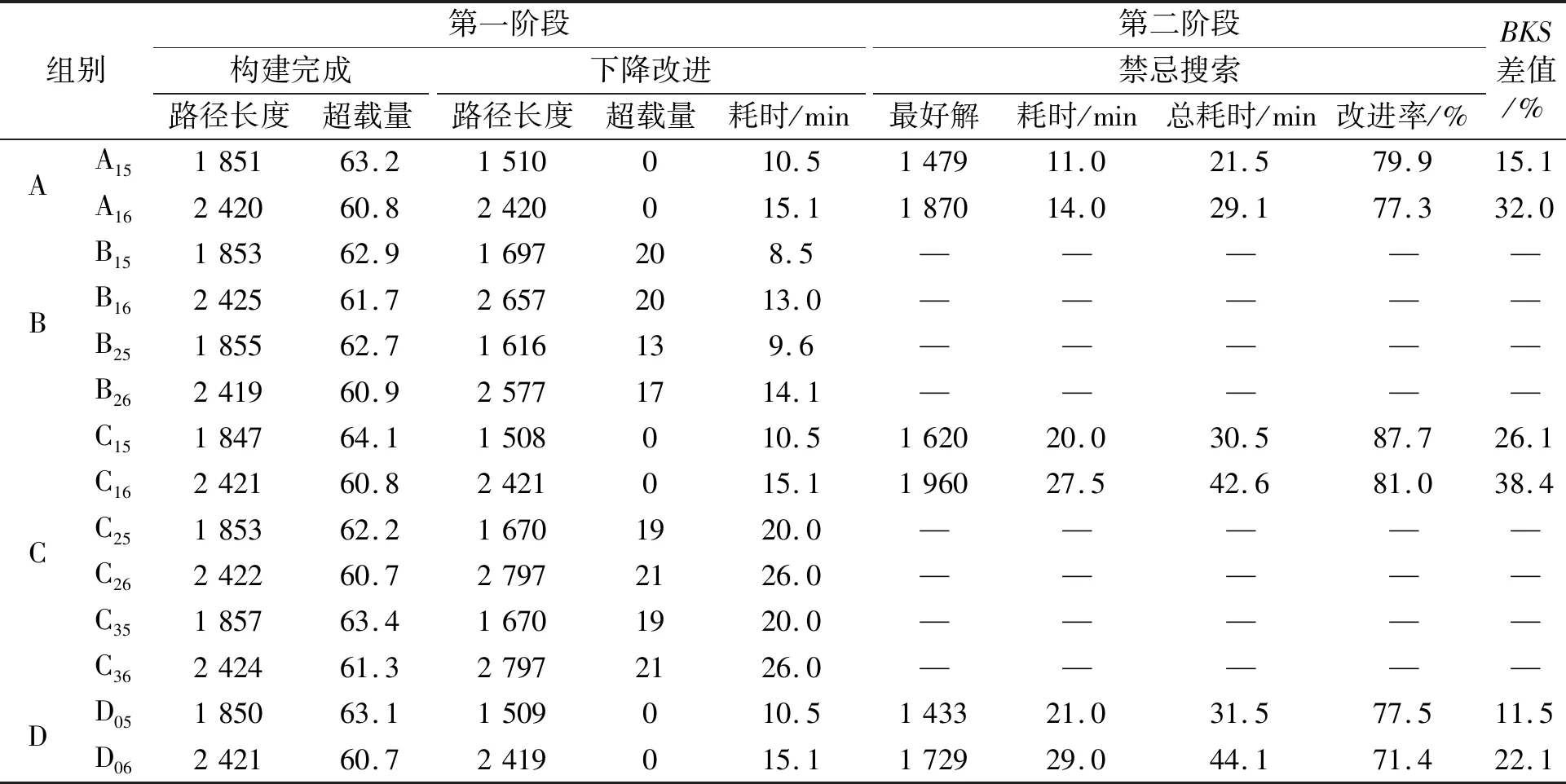
表4 数据III的实验结果

3.3 结果分析

由表2～表4可知，此次最好实验结果的平均BKS差值为10.5%，小规模与中等规模算例最好解的平均BKS差值为4.0%。虽与历史最好解有差距，但整体的求解质量是可靠的。

在路径构建阶段，相同算例数据构建后的路径长度仍存在差异，这是由于路径生成算法的随机性造成的，随机性的设置是为了增强算法搜索的多样性。在禁忌搜索阶段，6个算子A1x的最好解相比于D0x，平均有3.02%的差距，但在求解时间上少了21.7%。数据II和数据III中，B1x无法达成此阶段的优化目标，无法使超载量降为0。数据III中，B2x也无法将超载量降为0。数据I中，C1x组与A1x组的最好解差距不大。数据II中，C1x组与D0x组的最好解差距约为4%，求解时长也增加了3倍。数据I中，C2x组和C3x组下降改进阶段的求解时长和路径长度都差于D0x组，在最好解上也差于D0x组。数据II和数据III中，C2x组和C3x组都不能达到下降改进的优化目标。

从以上结果可以看出，在下降改进阶段，算子的数目不宜过少，算子过少无法达到下降改进阶段不超载的目标。在数据I和数据II的实验中，下降改进阶段和禁忌搜索阶段使用充足的算子，会得到更好的结果，但同时需要更长的求解时间。其中，下降改进阶段若只使用两类算子，虽然也能够完成最终的搜索，但是降低了求解质量并增加了禁忌搜索阶段的求解时间。

根据不同算例在不同组别中下降改进阶段结束后的路径长度绘制折线图，如图3所示。根据不同算例在不同组别中，实验最好解的路径长度绘制折线图，如图4所示。其中，数字1～6为各个算例的编号。

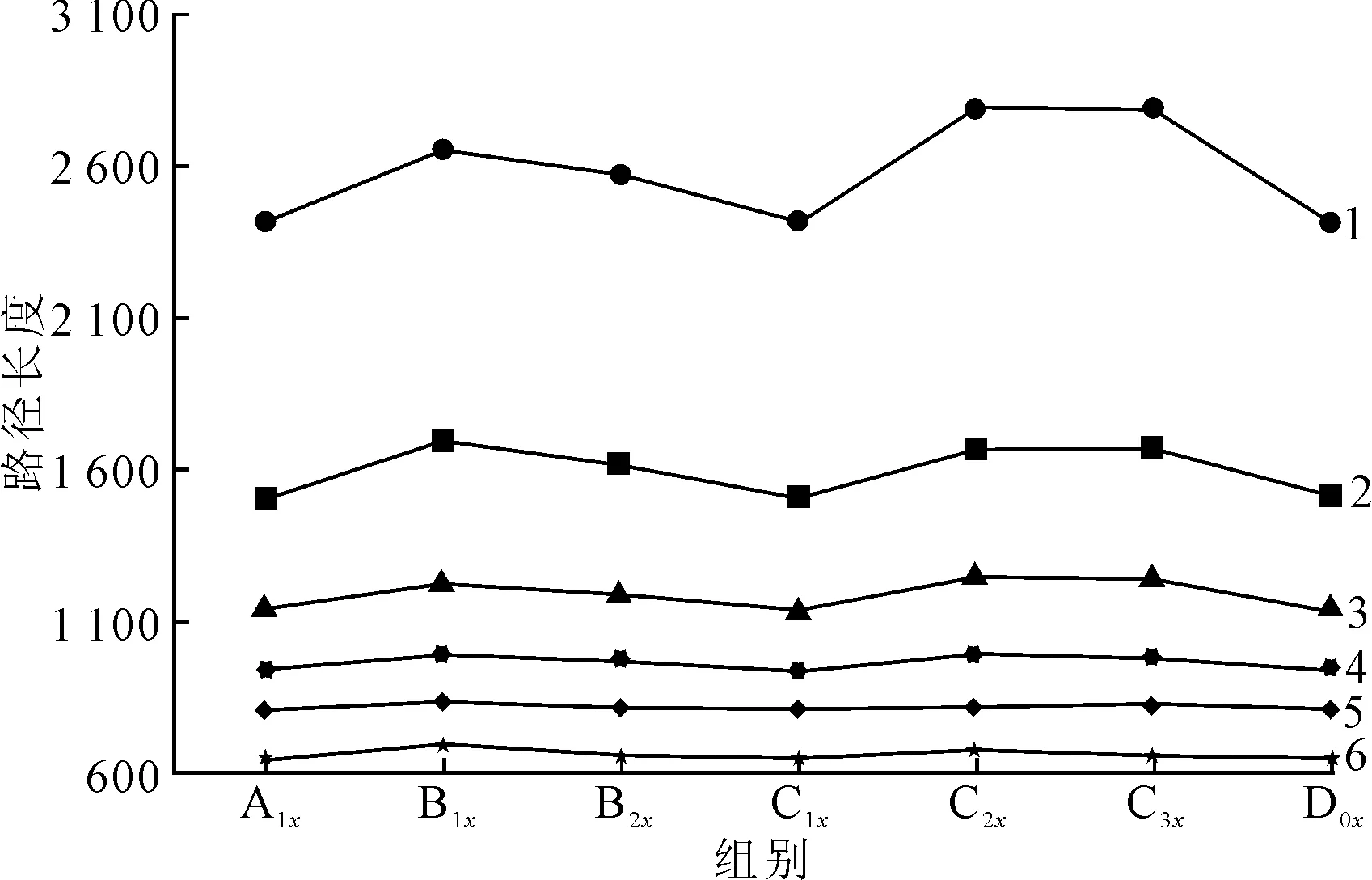
图3 下降改进阶段路径长度

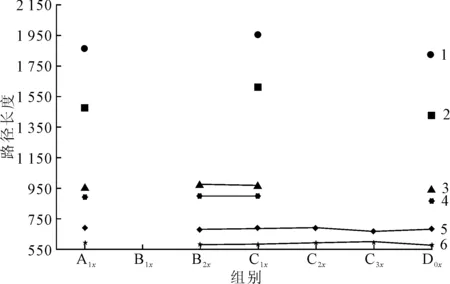
图4 实验最好解的路径长度

在实验中，算子的使用数量与实验结果质量呈现正相关性，在不严格限制求解时间的情况下，应尽量同时使用3类算子。同时，求解质量与算子顺序相关度较大，结果表明解的质量受顺序方式影响不大，受逆序方式影响较大，尤其在数据规模较大时(如数据II和数据III的C2、C3组)，求解质量会受到极大影响，为保证求解质量，建议使用顺序方式执行算子。