渐添条件驱动学程,学程变构走得更远
2020-09-21陈燕
陈燕
【摘 要】 复习课的重点是引导学生复习所学知识内容、梳理知识架构、感悟思想方法,综合了知识原理、方法技巧、创新思维等要素。本文以《轴对称》章末复习教学为例,以教学条件的分层设置为导向,探讨学程的合理变构在初中数学复习课中的应用。
【关键词】 初中数学;章节复习;类比学习
复习课是对所学内容的再加工、深化过程,需要引导学生在概念、定理、公式、法则的基础上将所学的知识点串联起来,形成完整的知识架构,对尚未掌握的知识进行加工与提炼。这就要求教师在复习教学中帮助学生真正做到理解数学,完成学程的合理变构,创设层次化的教学情境,通过条件的变化来深化学生的思维,逐步凸显思想方法,注重学生对于知识的自主生成,促进学生的全面发展。
一、强化基础训练
几何部分的基础内容是指组成几何图形最简单的图形要素以及能够阐述应用条件与方法的内容,往往涉及线段、角等要素的组合。充分挖掘基本图形的性质既能够帮助学生打牢基础,也是实行分层教学的重要内容组成,有利于不同能力水平的学生共同进步,构建完备的知识网络。
【案例1】画出Rt△ABC,并在其右侧添加一条直线,绘制出Rt△ABC关于该直线的对称图形。
【教学解析】在该层次的教学中,以巩固基础为主,帮助学生进一步理解轴对称、轴对称图形的基本性质。在采用几何定理方法绘制Rt△ABC关于某一直线的轴对称图形的基础上,可以组织学生借助平面直角坐标系来进行轴对称变换,确定轴对称变换过程中几何原理与坐标关系之间的对应性,进而加深学生对轴对称、轴对称图形的基本概念及相关性质的理解。
二、落实综合应用
在巩固、完善基础概念教学后,需要进行进一步的提升,设计高一层次的综合应用教学,提升学生对于轴对称相关概念、性质的应用能力,这是对前期相关理论学习的必要补充,也是进行后续延伸教学与创新训练的基础。
【案例2】已知:Rt△ABC,∠ACB=90°,AC=BC。
(1)在△ABC内部添一条与AB平行的直线,分别与AC、BC相交于点D与点E,试确定所得的新三角形CDE的形状;
(2)将△CDE绕点C逆时针旋转α°(0<α<90),则AD=BE是否仍然成立?若成立,请证明,若不成立,请说明理由;
(3)若M、N分别是线段AD、BE的中点,连接CM、CN、MN,判断△CMN的形状,并给出证明。
【教学解析】对于这种探究类、动态性的几何问题,学生具备一定的探索积极性,有助于他们积极投入到复习课程中来。在综合应用训练中,三个题目具备一定的递进关系,通过逐渐添加条件并加大难度来推动应用教学的深入开展,也符合学生的认知习惯,即由易到难,由浅入深。第一个问题较为基础,学生很容易就能给出结论;第二个问题训练了学生的画图能力,而0<α<90这一个角度范围其实是降低了难度,在完成解答的基础上要积极引导学生深入思考,采用类比的方法解决当90<α<180时,图形该如何画及结论该如何证明的问题;第三个问题较为复杂,能让学生直观感受到复杂的问题可以拆分成一系列基本的图形,在解决大题时养成认真读题及审题的良好习惯,尝试将其拆分成自己熟悉或掌握方法的基本问题。通过层次化教学方式,学生自然能够理解,如果α的范围未给出,就需要通过分类讨论的方法来进行求解。
三、科学拓展提升
复习课是培养学生创新思维能力的重要途径,《轴对称》复习教学中,不仅要综合应用轴对称图形知识,还需要创新使用轴对称的性质解决问题,将相关的研究方法迁移到对新图形的研究中,引导学生感受数学知识与方法的整体性。
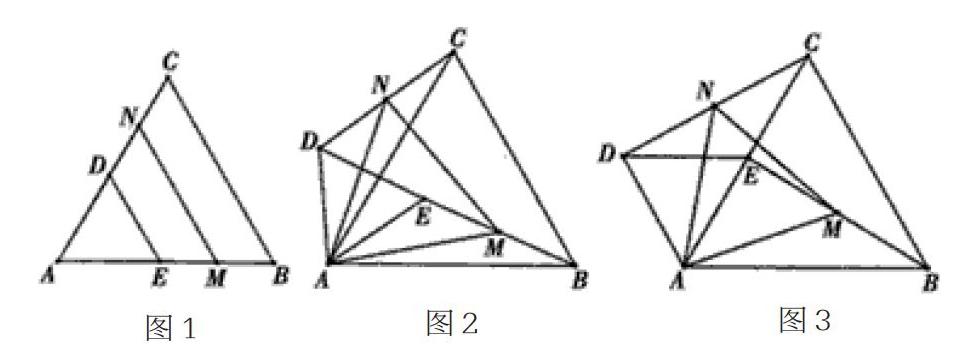
【案例3】已知△ABC和△ADE為等边三角形,M、N分别EB、CD的中点,如图1所示。易知CD=BE,△AMN是等边三角形。
(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立,请证明,若不成立,请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是,请给出证明;若不是,请说明理由。
【教学解析】学生通过类比方法解决此题,能够直观感受到解题方法的相通性,明白在解决难题时的一般策略就是分解图形,将复杂图形简单化,同时又在解题过程中感受等边三角形的性质及判定方法。
从提高复习教学的整体性和提高学生系统思维能力的角度来看,采用逐层深入、学程变构的思路能够起到更好的效果,引导学生逐渐加深理解,对相关的概念与方法进行迁移,进而获得新的知识,实现高质量的学习成果“再生长”。
【参考文献】
[1]黄淑莲.在“学为中心”课堂教学模式下如何上好复习课[J].基础教育论坛,2018(17):12-13.
[2]陆志强.学程变构,指向学生的自主发展——“平方根”教学实践及反思[J].中国数学教育(初中版),2018(7):76-80.
