基于高阶同步压缩变换的行星齿轮箱声音信号共振频带特征提取

张郑武，冯志鹏，陈小旺

北京科技大学机械工程学院，北京 100083

行星齿轮箱故障诊断具有重要意义[1−4]. 目前，行星齿轮箱的故障诊断研究主要基于振动信号的测试分析，对声音信号鲜有涉及. 声音信号蕴含着机械设备自身的结构和运行状态等重要的信息. 行星齿轮箱运行过程中产生机械振动，并引发空气振动向四周传播，从而产生声音信号. 其中，齿轮啮合产生的冲击和振动是行星齿轮箱的主要声源. 相对于振动信号，声音信号可通过非接触的方式采集，具有安装简便、操作简单等优点[5]，尤其当处在高温、高腐蚀环境下振动传感器无法使用时，仍能从声音信号中获得可靠的机械设备重要信息. Lin[6]对机械系统声音信号进行小波降噪，并成功提取了车辆发电机的故障特征；Rezaei等[7]利用多个声音传感器对不同转速和负载下的滚动轴承声音信号进行了实验分析；Metwalley等[8]将齿轮箱正常与故障状态下的声音信号时域、频域特征进行比较，判断了齿轮故障的严重程度. Bayda和Ball[9]将声音信号与振动信号进行比较分析，发现声音信号在早期故障的诊断方面具有优势.

然而，目前针对行星齿轮箱的声音信号特征提取理论方法还十分有限. 行星齿轮箱具有特殊的齿轮结构和运动形式，齿轮啮合点与故障接触位置具有周期性变化的特征，因此振动信号存在复杂的幅值−频率调制特性[10−11]. 进一步考虑声音传播过程的影响，实际测得的声音信号结构更加复杂，其频率结构及故障特征分布规律尚未明晰.

传统的齿轮箱故障特征建模与提取大都以齿轮啮合频率或其倍频作为载波频率，集中在啮合频带进行故障提取. 然而行星齿轮箱常在时变转速条件下运行，其啮合频率及调制边带随转速变化，容易与共振带交叉，增加故障特征的提取难度. 齿轮故障引起的冲击会激发行星齿轮箱共振，并对共振频率产生幅值调制和频率调制作用[12−13].同时，作为载波频率的共振频率不随转速变化，在共振频带进行故障特征提取，能够有效避免频率交叉现象，为时变工况下的齿轮故障诊断提供新的思路. 因此，本文首先建立行星齿轮箱声音信号的调幅−调频模型，并推导其故障特征分布规律.

另外，行星齿轮箱非平稳声音信号的故障特征提取仍是目前研究难题和热点之一. 传统的时频分析方法包括线性时频分析方法，如短时Fourier变换和连续小波变换；以及双线性时频分布，如Wigner−Ville分布、Cohen类分布等[14]均可用于分析时变信号. 但短时Fourier变换和连续小波变换受Heisenberg不确定性原则的限制，无法同时获得良好的时间分辨率和频率分辨率[15−16]，Wigner−Ville分布虽然改善了时频分布的分辨率，但存在着交叉项干扰而不适于多分量信号分析[17]. Auger和Flandrin[18]提出了时频重分配的方法，有效提高了时频可读性，但存在计算量较大问题；Daubechies等[19]提出了同步压缩变换方法，进一步提高了时频分析的可读性并保留了可逆特性，但难以抑制时间方向上的模糊现象[20−23]；Pham和Meignen[24]以及Oberlin等[25]在同步压缩变换的基础上进一步提出了高阶同步压缩变换方法，相比传统同步压缩变换而言具有更精确的瞬时频率估计模型，适合于分析快速变化的频率成分.

本文建立了行星齿轮箱近场声源声音信号在共振频带内的齿轮故障调幅−调频模型，推导时变工况下的声音信号的时变频率结构；并利用高阶同步压缩变换分析方法对声音信号进行故障特征提取.

1 声音信号共振频带调制模型

根据声源与传感器距离的不同，声场模型可分为近场模型和远场模型. 本文重点研究行星齿轮箱声音信号的近场模型. 根据声学理论，声压方程可表示为：

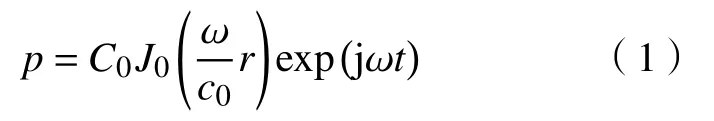
式中，p为声压，r为声源辐射半径，ω 为声源角频率，c0为声速，C0为常数，t为声音传播时间，j为虚数单位，J0(·)为第0阶贝塞尔函数，可表示为：

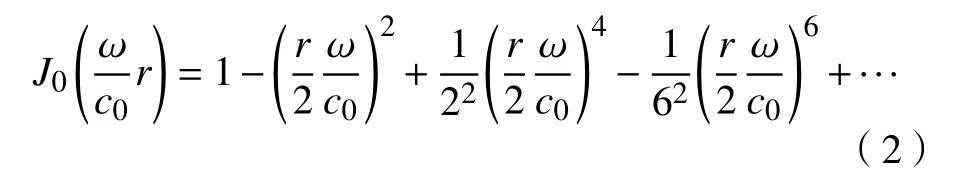
式（1）描述了声音传播过程中，声压与传播距离及声源频率的关系，声音信号中声源频率成分保持不变，但幅值在传播过程中逐渐衰减，衰减形式如式（2）所示. 幅值衰减因子C0J0(ωr/c0)可用来描述声音信号的幅值衰减. 当行星齿轮箱齿轮出现故障时，故障齿轮在运行过程中与其他齿轮啮合产生冲击，激发齿轮箱共振. 在系统阻尼作用下，共振迅速衰减，又在后续冲击激励下重复出现，对共振频率产生幅值调制和频率调制作用. 这种重复出现的共振产生声音辐射，因此声音信号在共振频带包含齿轮故障特征信息. 通常，近场声源的声音信号采集时，声音传感器的位置相对于声源距离较近且固定不变，加之共振频率仅受系统动力学参数决定. 因此，声音信号的幅值衰减因子C0J0(ωr/c0)可近似为常数. 结合行星齿轮箱振动信号的调制形式[12]，由振动产生的对外辐射的声音信号可表示为：

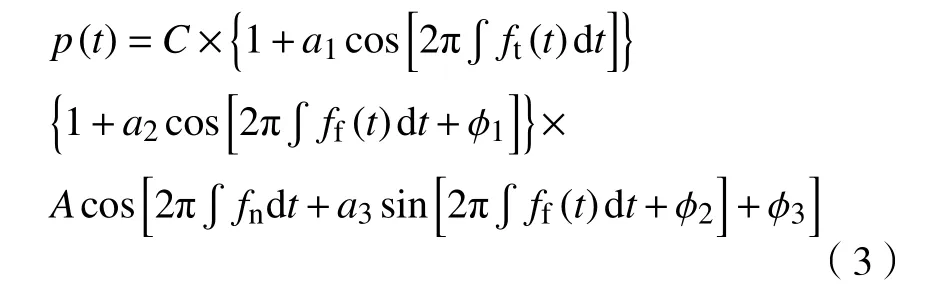
其中，C为幅值因子，A代表共振信号强度，a1、a2为幅值调制系数，a3为频率调制系数，ϕ1、ϕ2和ϕ3为对应的初始相位. 对（3）进行Fourier变换展开，得到声音信号内含有的特征频率结构为：

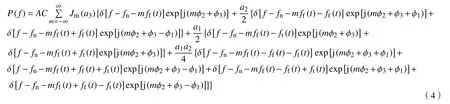
式中，m代表Bessel函数展开的阶数，fn为共振频率，ft(t)为太阳轮旋转频率或行星架旋转频率（太阳轮或行星轮出现故障时由于传递路径的时变现象产生的调制频率，因齿圈固定，当齿圈故障时此项可略去），ff(t)为故障特征频率，Jm(·)为第一类Bessel函数，δ (·)为Dirac函数.

根据（4）可总结出时变转速工况下行星齿轮箱齿轮故障时声音信号的时变故障频率特征：在太阳轮故障条件下，声音信号的共振频带内存在分布于共振频率fn两侧的、间隔为太阳轮故障特征频率ff(t)和太阳轮旋转频率ft(t)的组合的一系列时变边带成分，即fn±mff(t)±nft(t)（其中m,n=0,1,2···代表公式4中的阶数，下同）；在行星轮故障条件下，声音信号共振频带内存在与共振频率fn间隔为行星轮故障特征频率ff(t)和行星架旋转频率ft(t)的组合的时变边带，即fn±mff(t)±nft(t)；在齿圈故障条件下，声音信号的共振频带内存在与共振频率fn间隔为齿圈故障特征频率ff(t)的时变边带fn±mff(t). 其中，故障特征频率对称分布在共振频率fn两侧，可根据声音信号的时变边带对称中心定位共振频率，并可通过识别时变边带信息，有效检测及定位齿轮故障.

2 高阶同步压缩变换

短时Fourier变换（STFT）是最为常用的时频分析方法之一，其本质是加窗的Fourier变换. 对于一个有限能量信号x(t)，其STFT的表达式为：

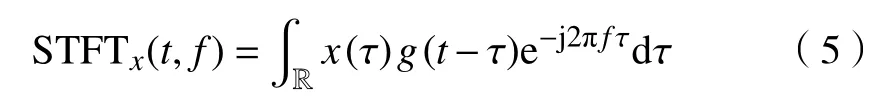
其中，τ为时间单位，g(t−τ)为窗函数. 由于窗函数尺寸固定，其时频分辨能力固定，在Heisenberg不确定性的制约下，难以同时得到复杂多变的瞬时频率细节的最佳表达.

基于短时Fourier变换的同步压缩变换方法（FSST）的关键思想是通过对瞬时频率进行精确估计，从而在频率方向上对时频能量进行重分配，FSST方法中，瞬时频率可根据短时Fourier变换的时频分布 S TFTx(t,f)计算为：

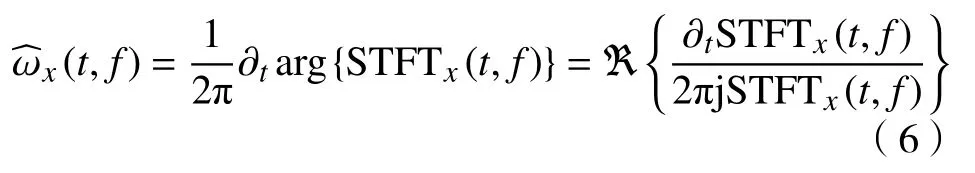
其中，ℜ {·}表示实数部分，基于此得到STFT频率重分配后的FSST结果为：

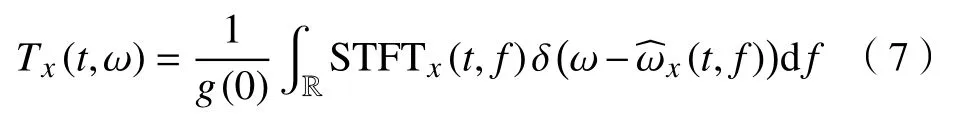
其中，g(0)为窗函数，由（7）可知，通过将频率方向上能量模糊压缩到瞬时频率脊线附近，可有效提高时频聚集性，有利于准确识别变化的瞬时频率特征.

然而，虽然FSST提高了时频分布的频域聚集性，但由于仅在频率方向上进行重分配，时域的能量溢出现象未得到有效解决，依然存在时频模糊问题. 为了克服这个不足，基于更精确的瞬时频率估计的二阶同步压缩变换（FSST2）被提出[25]. FSST2首先定义一个二阶局部调制系数：

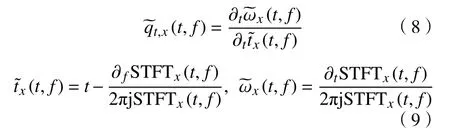
该调制系数为FSST瞬时频率估计（6）对时间t的一阶导数. 则二阶瞬时频率估计可表达为：

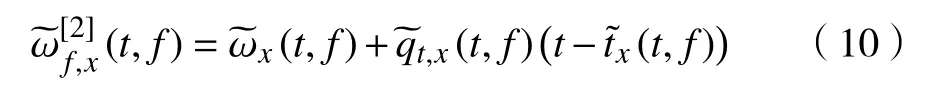
因而，信号x(t)的二阶同步压缩变换如下：

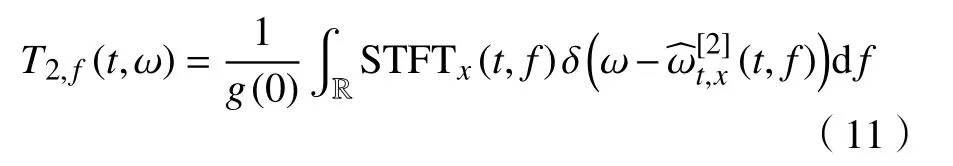
FSST2被证明能够提高具有高斯幅值调制信号的时频分布的效果. Pham和Meignen[24]针对其他更为复杂的快速变化频率信号，进一步提出了具有更为通用形式的高阶同步压缩变换方法（FSSTN）. FSSTN基于信号的幅值与相位的泰勒展开定义了新的瞬时频率估计：

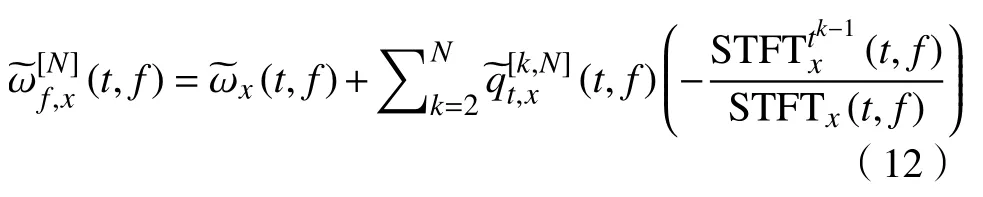
类似于FSST2，FSSTN的表达式为：

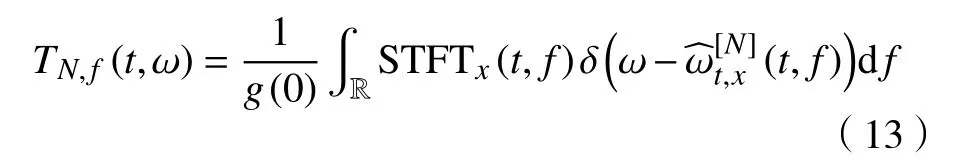
利用FSSTN方法，可以获得更加精确的瞬时频率估计，从而有效抑制时频模糊现象，使时频分布的可读性进一步提高. 根据实际应用需求，本文采用四阶同步压缩变换（FSST4），即取N=4.

3 仿真信号分析

在本节中，通过对时变转速工况下行星齿轮箱声音信号进行仿真分析，验证前文总结的时变故障特征规律形式，并验证FSST4方法提取共振频带内故障特征的有效性. 以太阳轮故障为例，由式（3）可得声音信号模型如下：

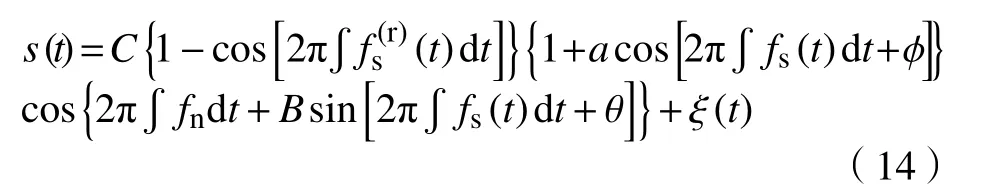
式中，fn为 行星齿轮箱共振频率，为太阳轮旋转频率，fs(t)为太阳轮故障特征频率. 取初始相位ϕ=θ=0，共振频率fn=2000 Hz，幅值调制系数a=1.2，频率调制系数B=0.1，幅值衰减因子C=0.98，加入信噪比为0 dB的Gauss白噪声 ξ (t). 令太阳轮旋转频率太阳轮故障特征频率为信号的采样频率为6000 Hz，时间长度为3 s.

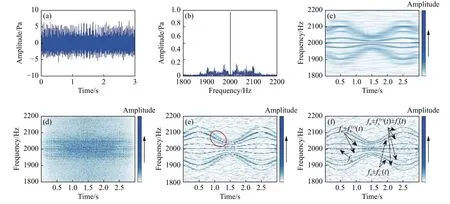
图1 仿真信号. （a）波形；（b）Fourier频谱；（c）STFT 时频分布；（d）Wigner−Ville 分布；（e）FSST；（f）FSST4Fig.1 Simulation signal:(a) waveform; (b) Fourier spectrum; (c) time-frequency representation(TFR) by STFT; (d) Wigner-Ville distribution; (e) timefrequency representation by FSST; (f) time-frequency representation by FSST4

仿真信号的分析结果如图1所示. 图1（a）和（b）分别为信号的时域波形和Fourier频谱分析结果. 图 1（c）、（d）、（e）和（f）为时频分布结果，右侧颜色条表征信号的幅值大小，颜色越深幅值越大（下同）. 由图 1（c）可见，STFT 虽然正确地显示出信号的瞬时频率变化趋势，但由于边带成分密集，且时频分辨率不足，时变故障特征提取困难；图1（d）Wigner−Ville时频分布虽然具有高时频分辨率特点，但存在严重交叉项干扰，无法准确辨识故障特征频率；图1（e）FSST时频分布尽管得到了较为清晰的瞬时频率变化趋势，但瞬时频率变化较快时，仍存在时间方向的模糊现象，如图1（e）中红色标记区域，因此难以精准识别密集分布的时变边带；图1（f）的FSST4时频分析方法相较于FSST采用了更为精确的瞬时频率估计公式，能够更有效地捕捉快速变化的频率信息，显著提高了时频分辨率.

4 实验信号分析

4.1 实验说明

本节进一步通过实验信号分析验证声音信号共振频带的时变故障特征，以及FSST4时频分析方法在实际行星齿轮箱故障诊断中的效果. 该实验在加拿大Ottawa大学机械工程系实验室完成.行星齿轮箱实验装置如图2，实验台由电动机、两级行星齿轮箱、定轴齿轮箱、转速计、加速度传感器、声压传感器和磁粉制动器构成. 各级齿轮箱齿轮齿数见表1. 根据各齿轮箱的齿数参数以及输入转频fd(t)，可计算得各齿轮故障特征频率，见表1.其中分别为一级行星齿轮箱的太阳轮旋转频率、太阳轮故障特征频率、行星轮故障特征频率和齿圈故障特征频率.

实验包含健康和故障状态下两组. 在健康状态下，各齿轮理论上均无故障；在故障状态下，人为在第一级行星齿轮箱的太阳轮上加工轮齿磨损，如图2所示. 两组实验的运行工况相同，电动机转频在30 Hz上下正弦波动，其中最大转频为40 Hz，最小转频 20 Hz，电机转频表达式近似为fd(t)=30+10sin(0.06πt). 声压传感器的采样频率为 20 kHz，采样时间为 25 s.

4.2 实验信号分析

4.2.1 正常状态信号分析

正常状态下，传统的STFT时频分析方法和FSST4时频分析方法被用于该声音信号分析，所得到的时频分布如图 3（a）和图 3（b）. 由图可知，FSST4时频分析方法获得了更好的时频分析效果，可读性更高. 根据行星齿轮箱共振频率不随转速变化的性质，以及在共振频率两侧呈现对称分布的调制频率边带特点，识别出共振频率为5003 Hz. 进一步验证共振频带内的时变频率边带，可得调制频率为电机转频，即存在时变频率成分如fn±fd(t)、fn±3fd(t)和fn±5fd(t). 由于制造及安装误差，齿轮旋转频率对振动及声音信号的调制作用难以避免，由于未检测到明显的故障频率调制边带，表明齿轮未出现故障，与实际情况相符.

图2 实验装置. 1—电动机；2—定轴齿轮箱；3,5—行星齿轮箱；4—声压传感器；6—磁粉制动器；7—太阳轮故障Fig.2 Test rig:1—motor; 2—fixed-shaft gearbox; 3, 5—planetary gearbox; 4—microphone; 6—magnetic powder brake; 7—sun gear fault

表1 齿轮箱主要参数Table 1 Main parameters of gearboxes

4.2.2 太阳轮故障信号分析

引入太阳轮故障后，在相同工况下采集的声音信号，利用STFT和FSST4时频分析方法分别对太阳轮故障状态信号进行分析，结果如图4（a）和（b）所示. 同样，FSST4获得更好的时频分析结果，依据共振频率的时不变特性及共振边带对称分布特点，可识别出共振频率为5003 Hz，与正常状态下的共振频率一致. 利用FSST4方法的高时频分辨率优势，可识别出一系列共振调制边带. 相较于图3（b）中健康状态下的信号时频分布结果，故障状态下还存在额外的系列边带，包括太阳轮故障频率fs(t)在电机转频的调制边带fn±fd(t)、fn±3fd(t)成 分 两 侧 的 额 外 边 带fn+fd(t)±fs(t)，fn−fd(t)±fs(t)，以及fn+3fd(t)±fs(t)，fn−3fd(t)±fs(t).通过与健康状态的分析结果对比，这些故障相关的时变边带表明行星齿轮箱的太阳轮出现了故障，与实际情况完全吻合.

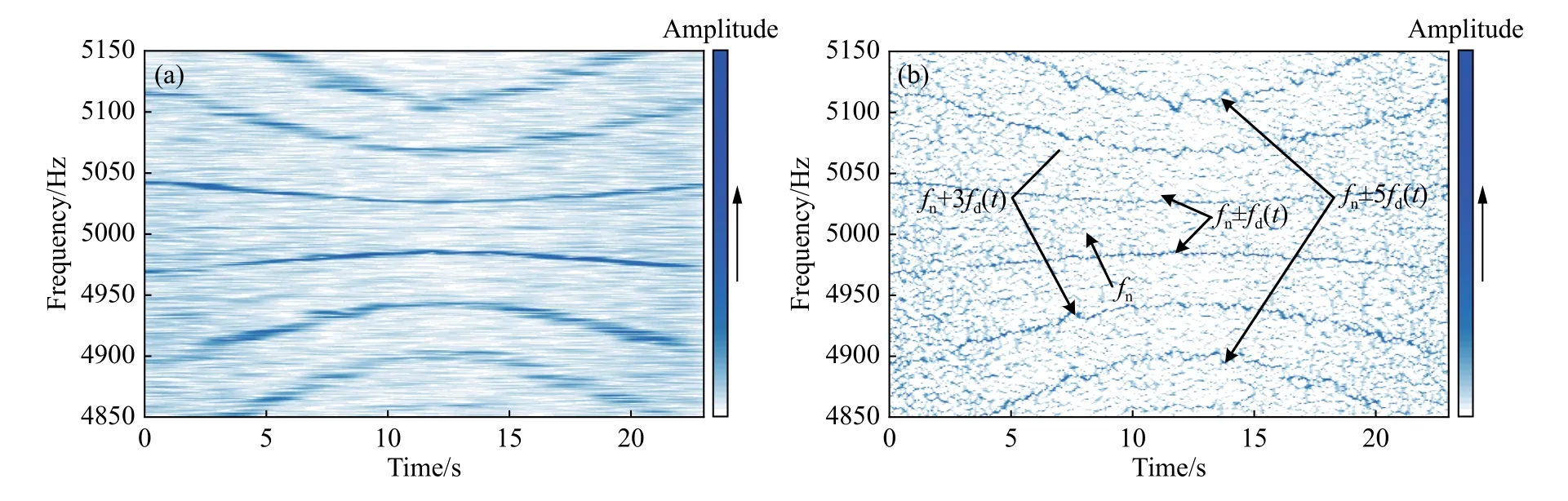
图3 正常状态声音信号分析. （a）STFT 时频分布；（b）FSST4 时频分布Fig.3 Acoustic signal analysis under normal conditions:(a) TFR by STFT; (d) TFR by FSST4

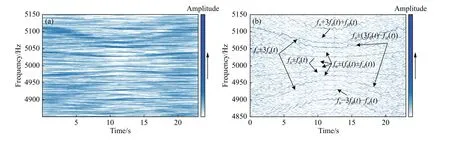
图4 太阳轮故障状态声音信号分析；（a）STFT 时频分布；（b）FSST4 时频分布Fig.4 Acoustic signal analysis under sun gear fault conditions:(a) TFR by STFT; (b) TFR by FSST4

5 结论

声音信号中蕴含着机械装备运行过程中的健康状态信息. 本文首先建立了行星齿轮箱近场声源声音信号共振频带调制模型，并推导了非平稳工况下齿轮故障特征时变边带在共振频率两侧的分布规律. 进一步利用共振频率不随转速变化的特性，在行星齿轮箱声音信号中准确识别了共振频率. 最后，在行星齿轮箱声音信号共振频带故障特征分布规律的指导下，应用高阶同步压缩变换方法，克服了传统时频分析方法时频分辨率低及干扰项严重的不足，实现了密集时变边带的准确识别，准确提取了时变的行星齿轮箱太阳轮故障特征. 通过数值仿真和实验信号分析，验证了声音信号共振频带调制模型和故障特征规律的准确性，以及共振频率识别方法和高阶同步压缩变换提取时变故障特征的有效性，成功诊断了行星齿轮箱的齿轮故障.