电动分离统一理论

陈 义

(淮阴工学院, 江苏 淮阴 223001; 中国科学院化学研究所, 中国科学院活体分析化学重点实验室, 北京 100190;中国科学院大学, 北京 100049; 北京分子科学国家实验室, 北京 100190)

从理论上统一毛细管电泳(CE)、传统电泳(EP)、离子淌度谱(IMS)、质谱(MS)等方法,有助于系统化它们并向更高层次发展。不过这些方法各有历史,各显其专,各有门户,统一不易。比如电泳,其历史并非始于1807年Reuss的黏土电动实验[1], Gautherot在1801年就已观察到了水滴会在两通电金属板间移动[2],而Bose则早在1740年就用电场来诱导喷雾了[3-6]。这比1850年Runge用莎草纸(色谱)来鉴别掺假色素[7]还早110年。电泳初名ionophoresis、cataphoresis等,1909年Michaelis称其为electrophoresis[8],这与Tswett在1906年命名色谱[9,10]相差无几。从1930年后Tiselius的移界电泳开始,到1940～1970年的纸和凝胶电泳建立,再到20世纪80年代的CE爆发,电泳经历了从低效到高效、从宏量到微/痕量、从纯电泳到色谱等多机制交融[11]的发展过程,已成为蛋白质、核酸等分离分析的一个金标准,卓然独立。又如MS,从1899年Thomson发现氖同位素算起[12],已发展120年,创建了诸多精美的电磁调控模式,用以囚禁离子或令其作复杂曲线飞行,在质量测量中一家独大。就算IMS,虽本名气相电泳[13,14]或等离子体色谱(plasma chromatography)[15,16],历史不长,却因美军在越南为探测丛林里人类气息[17]而得发展,现多涉安全,隐然自立。

统一虽难,但所想并非无据,亦有历史。它缘起于1984年作者初做CE不久,后因涉猎MS而有所行动,遂发现它们果能溯源至同一方程。

1 电动分离基本方程

分离源于运动之速度υ不同。带电量q的粒子,会在电场E中受力FE=qE因而获速,并因各种阻力∑Fi而减速。已知E是电势φ沿l方向的导数,即E=dφ/dl,且电场中离子的运动须遵守牛顿力学第二定律F=ma。由F=FE-∑Fi与a=dυ/dt,得:

(1)

式中m是带电粒子质量,t是时间,μ=υ/E称作淌度。方程(1)即为统一电动方程,是关于速度或淌度的一阶微分方程。若设阻力均与速度成正比,即∑Fi=∑fiυ=∑fiμE,由初始条件μ|t=0=0可得方程的解:

(2)

式中fi是阻力系数。显然,阻力压制了离子的加速过程,设到时刻τ后指数项趋于零,运动变成恒速稳态,则按e-x≈1-x=0有:

(3)

加速时间τ与粒子质量成正比,而与阻力系数成反比。可由此推论:1)由加速时间可测定离子质量,但尚未见多少研究报道,或能成质谱测量新模式;2)电场中离子的迁移状态与介质密不可分,真空、气相、液相各有不同。下面分别讨论之。

2 真空电迁移

2.1 飞行时间质谱

真空无阻力,若离子沿l方向飞行,令q=ze、υ=L/t,在(0～υ,φA～φB)区间积分可得方程(1a)的解为:

(4)

式中L为飞行距离,z为价态,e为电子电量,φAB为电压。如两离子的z相等,则时间分辨率为:

(5)

显然,时间分辨率随电压非线性降低而随飞行距离线性增加,但受空间限制,飞行管不能过长,一般数米,故质量分辨率m/Δm仅达万级,还需要超高速检测。比如在100 V/cm下m/z=1 000的离子飞行2 m需时仅32 μs,必须有ns级检测响应并配MHz级多路采样接口。

2.2 磁质谱与双聚焦质谱

电场加速后,离子可从β角度注入磁场B,让磁力FM=qυBsinβ改变其飞行方向。若β=0,离子会继续直线飞行;而β=90°时sin90°=1,FM最大并向心,以抵抗飞行离心力(mυ2/R,R为半径)。两力平衡时:

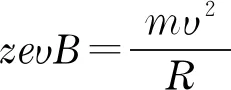
(6)

若m/z相同,υ越大则R也越大,即磁场能色散速度。合并式(6)、(4)得:

(7)

即欲定R测不同m/z离子,则需调节B或φAB。因m/z受控于多个参数,磁质谱分辨率多在万级,但双聚焦能提高分辨率到10万以上。双聚焦利用了磁、电的速度色散作用。将式(6)的磁力用侧向电场力zeE┴替换,有:

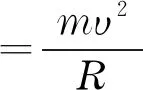
(8)

由R∝υ2可知,电场对速度的色散能力强于磁场。联用公式(8)和(6),让离子顺序穿过扇形电场和磁场,作两次弧形飞行,可聚焦离子,提高质量分辨率。原因是m/z相同的离子,速度大则弧长,速度小则弧短,最终会同时到达检测器。

2.3 回旋共振质谱

把角频率ω=υ/R=f/2π代入公式(6),整理得:

(9)

即质量分辨率随B线性增加,在超导强磁场(>9 T)下可达百万级别,是高分辨质谱。因Δm∝Δf,质量分辨率也受制于频率分辨率,但由频率测质量,可用射频共振法,结合傅里叶变换,便开创了测量质量新模式。

2.4 四极杆与离子阱

若离子从其他角度进入磁场,则会作螺旋飞行。类似地,借电场亦可调变其飞行轨迹甚至囚禁离子,此即构建四极杆、离子阱、轨道阱等质谱的理念。四极杆质谱可采用以下调控场:

(10)

式中φdc、φac分别指直流、交流幅值,r0为四极杆围出的半径(见图1)。离子因此受到的侧向力为:

(11)

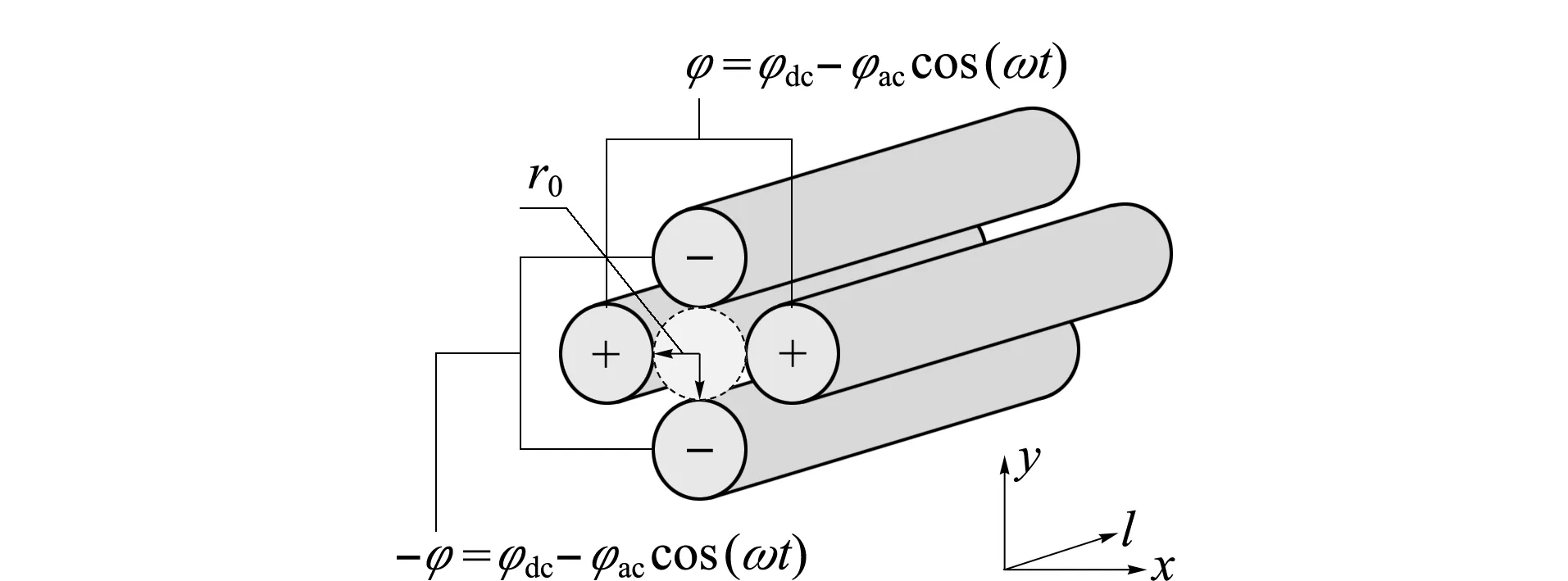
图 1 四极杆质量分析器结构、坐标与调制电场Fig. 1 Structure, coordinates, and modulated electric field of a quadrupole mass analyzer

结合式(1)得二阶偏微分运动方程:

(12)

φac=0时的解为:

(13)

即在四极杆上施加恒电压,则离子在y方向的飞行轨迹稳定,但在x方向不稳。令

(14)

得φ不恒定时的Mathieu方程:

(15)

此方程已有详解[18,19]。从已知解看,当离子在径向和纵向都稳定时,就变成了离子阱;若在l向增加一直流电场,就变成了线性离子阱。

2.5 轨道阱[20]

建立如图2所示的柱坐标系统,对纺锤形内电极和凸肚形圆筒外电极施加由四极场和圆柱形电容对数场合并成的电势,就得到了轨道阱调控场:

(16)

式中A是常数,K是电场曲率,Rm叫特征半径,r2=x2+y2。轨道阱的有用信息是l向的运动:

(17)

(18)

即轨道阱l向的f2与m反比,亦能采用频率和傅里叶变换来测量质量。注意f与能量或势阱无关,故能提高分辨率和质量测量的准确度;另外m与K成正比,即只增加K就能提高分辨率而无需强磁场,故而能维持高分辨,并有效降低操作与维护的成本。

图 2 轨道阱质谱分析器之旋转对称构型与柱坐标设置(虚线为离子轨迹)Fig. 2 Rotationally symmetric configuration of orbital trap mass spectrometer on a cylindrical coordinates, with a dotted line showing an ion trajectory

3 气相电动方程

气相中,离子在电场中飞行,会因粒子碰撞等产生阻力∑Fi=Fgr,可惜Fgr未知。为解方程(1),须先处理小离子(远小于自由程λ,如<1 kD)和大离子(≫10 kD),然后返回处理中间离子。

3.1 小离子电动方程

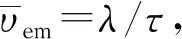
气体中会有3类碰撞:离子、气体分子的自我碰撞和离子-气体分子碰撞。样品离子一般都很稀少,自碰概率小而可略;气体分子多但其自碰却不影响离子行为;唯离子-气体分子相撞阻挡离子漂移。在数个大气压氛围中,气体分子连续碰撞两个以上离子的概率亦小而可略,仅离子-分子双碰撞不可忽略。各向同性碰撞前后动量须守恒,故:

(19)

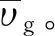
(20)

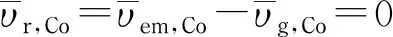
(21)

代入式(19)得:

(21a)

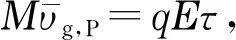
(21b)

(22)

(23)

(24)

合并式(21b)～(24),由PV=nkBT得:

(25)

3.2 大离子电动方程

若离子尺寸≫λ,便无法再自由行走。气体分子会围拢而来,攀爬在离子上,活像液体并出现黏滞阻力Fη,其值由Stokes公式Fη=fμemE确定,其中f=6πηr,f为黏滞阻力系数,η为气体黏度,r为离子切变半径。以氮气(常用)分离牛血清白蛋白为例,因r≈4.0 nm,m=66.43 kD=1.10×10-22kg(1 D=1.66×10-27kg), 200 ℃时η=2.46×10-5Pa·s,则τ≈m/(6πηr)=1.10×10-22/(6π×2.46×10-5×4.0×10-9)=5.9×10-11s=59 ps,即大离子经皮秒级加速便进入稳态:

(26)

式中d为离子自身密度。淌度与质量也是非线性关系(μ∝m-1/3),分辨率亦不高。大离子淌度也与q正比、与半径成反比,对电荷和尺寸有高分辨率。

3.3 中等离子电动方程

在大、小离子之间的离子,阻力不清,方程(1)虽适用却无法解出。有人基于大离子公式,结合试验结果,提出了多种半经验公式[21-24],其中以下公式较为简明[24]:

(27)

式中A1、A2、A3为常数。由此式可得到与大离子类似的结论。

4 液相电动方程

4.1 常规电泳方程

液相电泳阻力高于气相,溶液中除黏滞阻力Fη外,还有双电层影响,会出现反号离子的逆泳阻力Fcep和双电层变形的弛豫阻力Frl等。它们皆与υem成正比,FR=fυem=fμemE,故式(2)和(3)仍是方程(1)的解,不过r须是溶剂化半径。液相黏度比气相大10倍以上,电泳会更早进入稳态。仍以牛血清白蛋白为例,取25 ℃水,η=8.95×10-4Pa·s,有τ≈ 1.6 ps,即比气相快35倍;若取水中最小离子H+,由m=1.674×10-27kg,r=1.7×10-15m,有τ≈ 58 ps,略快于气相大离子。式(26)因此亦适合液相电泳,亦即μ∝q/r∝m-1/3,即对离子电荷、尺寸分辨率高于质量,其中尺寸分辨能力已被凝胶等筛分介质充分强化,成了蛋白质、核酸等生物大分子分析的金标准。

(28)

式中NA为阿伏伽德罗常数,代入球坐标泊松方程

(29)

由边界条件φ(r=∞)=0和公式(26),可解得离子淌度与切变面电位ζ的关系式:

(30)

式中ε为介电常数,1/κ为双电层厚度。f(κr)包含了电泳阻力和弛豫阻力,很难解析。Henry用分段处理法推得了一个复杂的Henry函数[25];而Ohshima则用试错法,借电动力学及边界条件,提出了更简明准确的公式[26]:

(31)

κr→0实为点电荷,κr→∞则为平板,但多数κr≈1～20,可用该式计算。式(30)显示μem是离子浓度、价数、介电常数、黏度的函数,这为分离提供了优化的依据,但与各参数测量并无关。为测量计,可设电泳沿方向l作一维迁移:

(32)

由此便有两套测量方案:定时分离测迁移距离LR与定长分离测出峰时间tR:

(33)

此两方案的峰位置均会受通道、电场和组分淌度(因而介质)等诸多因素影响,精密度颇难控制。

由电解质溶液之修正欧姆定律i=I/S=σE(i为电流密度,I为电流强度,σ为电导率),可将公式(32)变为

σSdt=μemIdt

(34)

在给定介质中做恒温分离,则淌度、电导率变化可忽略。在0～tR与0～LR区间积分得:

(35)

式中VR叫迁移体积,QR叫迁移电量,ρR叫迁移电密度。QR和ρR同归一系,皆能实时测量。由此式有另外两套测量方案:定VR测QR和定QR测VR。其中前一方案便于实施,给定分离腔即可,故予推荐。QR融合了电流(或V、E)随时间的变化,故能抗拒电场等参数变化;ρR还融合了通道尺寸等因素,可抗拒通道参数变化。QR、ρR测量应是新法,少见报道。

至此,我们有纯电泳的通用方程:

(36)

其中A为常数。该式前四式为测量方案,第五对应于原理,第六对应于应用。

4.2 CE方程

毛细管充入溶液,管壁两侧即形成双电层,液层一侧的反离子电泳会带动溶剂形成电渗。因毛细管很大,κr→∞即f(κr)=1,故:

(37)

式中μos为电渗率,ζCap为管壁切变面电位。电渗如泵,助推离子、分子按加和淌度μsum迁移:

μsum=μos±μem

(38)

石英、玻璃等毛细管电渗与正离子同向皆取正,负离子取负。毛细管壁如固定相,可保留组分。此色谱机制可由固定相或准固定相P强化,再次改变组分淌度:

(39)

式中n是组分的分子数,p为相数,μ可称为加权淌度。若仅取两相,则:

(40)

k即保留因子,可用离子或分子出峰时间测定。由此可知CE的通用方程是公式(39),结合式(36)、(38)和(40)可推导各种分离模式或实现各种测量。有兴趣者可参阅文献[11]。

5 结论

从牛顿力学第二定律可以推导出统一电动方程,它是关于速度或淌度的一阶非线性微分方程,其解与初始、边界条件有关,但阻力影响最大。本文从真空、气态和液态3种情况出发,分别推导了质谱、离子淌度谱、电泳和CE的运动方程。从这些方程可再推导出新的运动方程和测量模式。在推导中发现,介质中的电动加速过程很短,都在皮秒级,故气、液相中离子皆以恒速迁移。在电泳中,稳定的测量不是时间而是电量及其衍生方法。质谱中离子飞行于无阻力真空,能连续加速或加速后再自由飞行,其飞行轨迹可受磁场、交变电场调控,由此可构造飞行时间质谱、磁质谱以及四极杆、离子阱、轨道阱、旋共振质谱等。电场调制正是质谱创新发展的主流和前沿方向。由此可见,推导统一理论,不仅能条理化一些纷繁的仪器方法,还能开启发现或创新研究的新途径。