基于后悔理论的理想点决策方法及其在防洪调度中的应用
2020-09-18李英海李清清郭家力夏青青
汪 利 李英海,2 李清清 郭家力,2 夏青青
(1.三峡大学 水利与环境学院, 湖北 宜昌 443002;2.三峡大学 三峡库区生态环境教育部工程研究中心, 湖北 宜昌 443002;3.长江科学院 水资源综合利用研究所, 武汉 430010)
水库洪水调度是在保证水库水工建筑物安全的前提下,严格按照调度原则并充分考虑实际情况,对水库蓄泄进行合理安排,从而减少下游遭受洪水的危害.在实际的水库洪水调度中,决策信息的模糊性、决策者知识和经验的局限性以及决策者的心理行为等各方面的因素,都会导致决策者难以科学合理地对方案进行决策优选.那么,如何在水库洪水调度中充分考虑决策者受心理因素的影响,并做出科学合理的决策是亟待解决的问题.
近年来,大部分学者多采用模糊数学、概率统计和区间灰数3种方法对不确定性信息进行研究.而在水库洪水调度决策中运用模糊数学和概率统计方法会具有一定的盲目性,所以区间灰数就成为在描述不确定性问题时最为合适的方法[1].在水库洪水调度决策方面,常运用的方法主要包括:层次分析法、Vague集法、TOPSIS法、灰色关联度法、理想点法等[2-6].关于理想点法决策,王彦,孟令爽[7]建立评价指标体系,划分风险等级,将熵权法与理想点法相结合,对水资源承载力风险进行评价;危文广,黎良辉,赖敬飞,等[8]基于理想点法原理计算贴近度,构建水资源承载力评价模型;归力佳,顾圣平,林乐曼,等[9]利用组合赋权-理想点法对各方案进行综合评价,得出协同优化各目标的最佳蓄水方案.在上述研究中,决策者在决策过程中都是理性的,而在实际的决策中,完全理性决策的可能性很小,心理因素大多都会对决策者造成一定程度的影响,为此很多学者开始对决策者的心理行为与决策之间的关系与影响进行研究.在这一背景下,后悔理论[10-11]的提出引起广大学者的广泛关注.后悔理论是一个行为决策理论,充分考虑了决策者的心理行为.后悔理论具有计算较为简单、涉及的参数较少、决策者不需要给出参照信息的优点.因此,本文针对决策指标值为区间灰数的水库洪水调度问题,将后悔理论引入理想点决策中,通过构造正、负理想方案,决策者将各方案分别与正、负理想方案比较时会出现后悔和欣喜的心理行为,并得到后悔值和欣喜值,最后依据各方案的综合欣喜后悔值将水库洪水调度方案进行优劣排序.通过防洪调度决策实例计算与分析,验证所提方法的合理性与可行性.
1 区间灰数
1.1 区间灰数的定义
1.2 区间灰数的距离
定义1[13]设区间灰数产生的背景论域为Ω,μ)为灰数取值域的测度,则称go)=μ)/μ(Ω)为区间灰数的灰度,记为go.在缺乏区间灰数取值分布信息的情况下,若区间灰数为连续灰数,则=(a1+b1)/2为灰数的核.
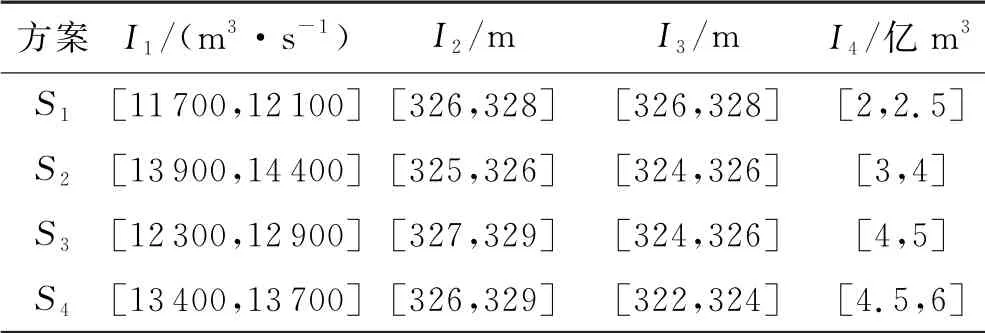
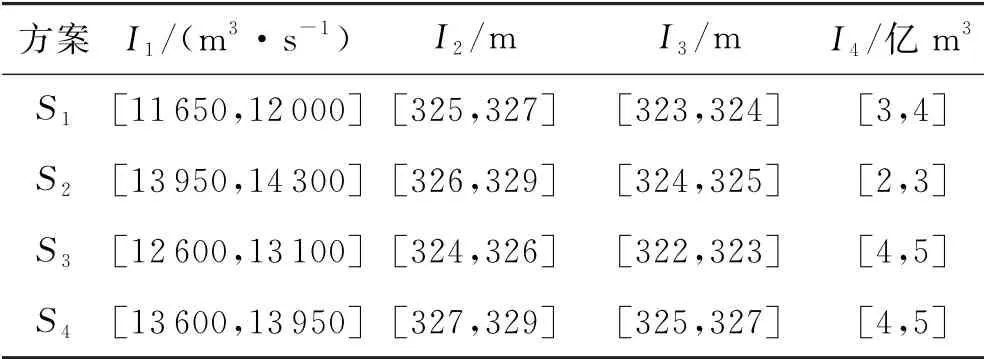
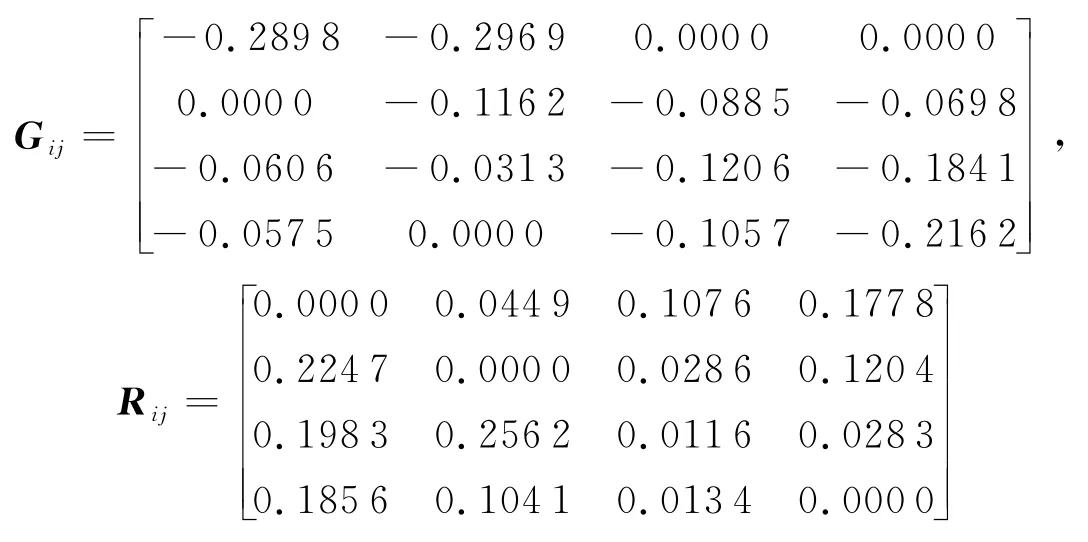
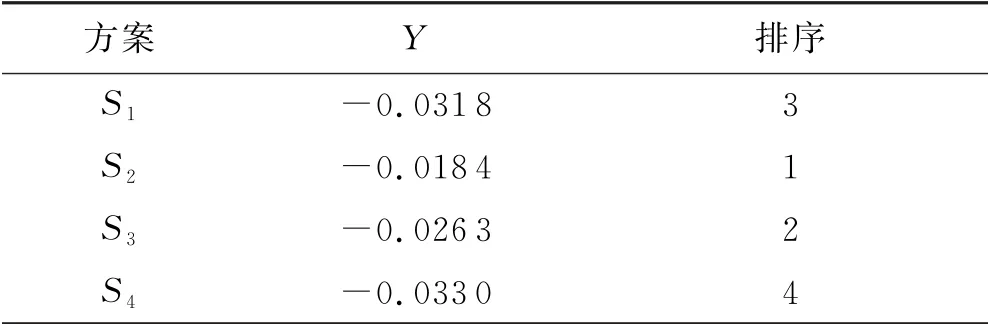
定义2[14]设有A)∈[a1,b1](a1 定义3设有A(⊗)∈[a1,b1](a1 为两区间灰数的距离. 假定调度决策有m个决策方案组成决策方案集S=(S1,S2,…,Sm),n个决策指标组成指标集I=(I1,I2,…,In).调度状态集为T=(t1,t2,…,tk),第k种状态下指标Ij发生的概率为Pk.指标权重为W=(w1,w2,…,wn).区间灰数xijk)为决策者在第k种状态的Ij指标下对方案Si的评价值,记为xijk()=]表示方案Si在Ij指标下的样本值的上限表示方案Si在Ij指标下的样本值的下限,(i=1,2,…,m;j=1,2,…,n)[16]. 方案集S对指标集I的评价值的样本区间灰数矩阵为: 由于各个决策指标之间存在性质或量级上的不同,所以需先对样本区间灰数矩阵进行标准化处理: 对于效益型指标: 后悔理论,顾名思义就是在做了错误的选择之后产生的懊悔的心理感觉.Loomes、Sugden和Bell在1982年都提出了后悔理论[10-11],这是一种在放弃独立性公理的前提下,在进行决策过程时,将后悔和欣喜这两种不同的心理行为同时考虑到该项决策中的理论.将进行决策的各方案与其心中的理想方案比较能够得到欣喜后悔值.若以正理想方案的决策指标值作为参考点,其他方案与正理想方案的决策指标值相比劣于正理想方案时,决策者由后悔理论可以判断出对于选择该方案的心理是后悔的;若以负理想方案的决策指标值作为参考点,其他方案与负理想方案的决策指标值相比优于负理想方案时,则决策者从后悔理论可以判断出对于选择该方案的心理是欣喜的.根据文献[11]可知,决策者对方案Si的决策指标值xij相对于正理想方案的后悔值函数Gij和相对于负理想方案的欣喜值函数Rij的表达式分别如下[14]: 式中:δ(0<δ<1)是决策者的后悔规避系数,δ=0时表示不后悔,δ越大,后悔规避程度就越大. 所以各决策指标总的欣喜后悔值函数为: 将基于后悔理论的理想点决策方法的决策过程进行归纳总结: 步骤1:根据已建立的决策指标体系构造评价值为区间灰数的样本矩阵,并根据公式(6)和(7)对各指标进行标准化处理; 步骤3:根据公式(5)确定两区间灰数的距离d,再根据公式(10)和(11)计算出各指标的欣喜值Rij和后悔值Gij; 步骤4:根据公式(12)、(13)以及指标权重wj求出各评价指标总的欣喜后悔值Yij和各方案的综合欣喜后悔值Y,并将其从大到小进行排序,确定最优方案. 以陕西某水库2009-10-03洪水为例进行实际决策调度[1].在洪水来水之前,水库的水位可能有以下4种状态:死水位k1、防洪限制水位k2、正常蓄水位k3和防洪高水位k4.针对洪水调度考虑了4个指标:最大下泄流量I1;水库最高洪水位I2;调洪末水库水位I3;弃水量I4.当水库水位分别位于上述4种状态时,根据以往的历史水文记录,4个指标的区间灰数决策指标值见表1~4[1]. 表1 k 1决策指标值 表2 k 2决策指标值 表3 k 3决策指标值 表4 k 4决策指标值 其中,状态概率表示上游水库洪水来水的可能性,各决策方案的不同状态发生的概率为Pk=(0.141 7,0.276 2,0.366 7,0.215 4),综合指标权重采用基于决策者决策差异度的准则权重确定方法,将专家主客观权重与指标权重相结合,综合指标权重确定为wi=(0.124 6,0.289 0,0.384 2,0.201 5)(具体方法及步骤见文献[1]). 利用本文提出的基于后悔理论的理想点决策方法,其决策过程为: 步骤1:根据公式(6)和(7)以及水库4种状态概率对表1~4进行标准化处理,得到一个无风险决策矩阵,见表5. 表5 无风险决策表 步骤3:根据公式(10)和(11)计算出各指标的欣喜值矩阵Rii和后悔值矩阵Gii.为保证对效益型指标和成本型指标的平衡处理,此时δ=0.5. 步骤4:根据公式(12)求出各评价指标总的欣喜后悔值Yij,再根据公式(13)以及指标权重wj求出各方案的综合欣喜后悔值,并将其从大到小进行排序,确定最优方案. 各方案综合欣喜后悔值见表6,这些数值表示决策者将各方案与正理想方案相比得到的后悔值和各方案与负理想方案相比得到的欣喜值之和. 表6 各方案综合欣喜后悔值 根据综合欣喜后悔值越大越优的原则,可以得到各评价方案的优劣排序为S2>S3>S1>S4,最优方案为S2,最劣方案为S4.其中最优方案S2的欣喜值为0.063 3,最劣方案S4的欣喜值为0.058 3,说明决策者将方案S4与负理想方案相比,决策者的欣喜程度低于将方案S2与负理想方案相比时;最优方案S2的后悔值为-0.081 7,最劣方案S4的后悔值为-0.091 3,说明决策者将方案S4与正理想方案相比,决策者的后悔程度高于将方案S2与正理想方案相比时.此结果与文献[1]灰色随机多准则的水库洪水调度群决策结果完全一致,说明基于后悔理论的理想点决策方法在水库洪水调度群决策中的运用是合理可行的. 本文针对决策指标值为区间灰数的水库洪水调度问题,提出了一种基于后悔理论的理想点决策方法,主要特点就是考虑了人的心理因素,将决策者的心理行为引入决策方法中.根据决策者将各方案与正、负理想方案比较时出现的心理行为得到欣喜后悔值,依据综合欣喜后悔值由大到小将各方案进行优劣排序.该方法不需要决策者给出参照信息,并且只涉及到δ一个参数,计算公式简单,易于求解.该决策方法的提出也为求解不确定性决策问题提供了新思路.
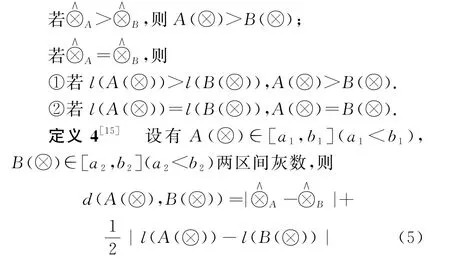
2 基于后悔理论的理想点决策方法
2.1 构造样本区间灰数矩阵及其标准化处理


2.2 正负理想方案

2.3 后悔理论


2.4 决策过程
3 实例计算与分析





4 结 论
