一种非条分法的均质土坡及均质地基土坡稳定安全系数新算法

赵四汉 单 君 胡永富 毛 斌

(浙江省交通规划设计研究院有限公司, 杭州 310000)

路堤边坡稳定性是公路建设质量控制的关键环节,目前工程设计中应用较为广泛的方法是极限平衡分析法.用该法进行稳定性分析分两步：第一步,对某一形状和位置已知的潜在滑动面,计算其稳定安全系数;第二步,对许多潜在的滑动面,确定相应最小安全系数的临界滑动面[1-2].第一步安全系数的计算通常采用条分法,需预先假定滑动面、土条划分等,且不同的土条划分方式和不同的条间力假设,其结果不唯一,加之计算公式为多项式求和以及第二步中需进行多次试算并搜索的特点,对一线工程设计人员来说,即使采用机算仍相对繁琐.

曾有学者将两步结合起来,以安全系数为目标函数,运用数学理论求其极小值,以期不需搜索直接解得临界滑动面和最小安全系数,从而提高计算效率,但均因各自的局限性无法在实际工程上应用.如Baker和Garber[3],Revilla和Castillo[4],Ramamurthy、Narayan和Bhatkar[5]采用变分法求极小值,但偏差较大并不理想,De Josselin和De Jong[6],Luceno和Castillo[7]等对变分法理论应用的正确性和分析问题的局限性也都提出了质疑,罗文强[8]和杨庚宇[9-10]均对条分法做了改进,将安全系数表达成积分的形式,分别采用变分法和多元函数的极值条件求极小值,但其仍是条分法的一种形式,且极值条件需要对至少3个自变量求偏导解超越方程组,计算复杂且往往得不出结果,蒋斌松[11]利用此法也仅给出了纯黏性土边坡(φ=0°)的结果.

本文针对均质土坡及均质地基土坡,不划分土条,不引入条间力假设,通过引入描述圆弧滑动面函数的3个自变量,以滑动体整体为研究对象并以其为积分域,由极限平衡原理建立积分形式的平衡方程,推导了稳定安全系数的理论函数表达式,并通过Mathematic编制了计算程序,提出了第一步中求解安全系数的一种新方法.基于二元函数的极值条件,通过降维度求极小值与迭代计算相结合,可直接确定临界滑动面的位置,无需进行试算和搜索,在实际工程中大大提高了计算效率且安全系数唯一.本文介绍第一步内容,通过一个经典算例对本文方法进行验证,并与条分法的计算结果进行对比,最后对本文方法和条分法进行比较探讨.

1 均质土坡

如图1所示,均质土边坡坡率为k,高度为H,土容重为γ,黏聚力为c,内摩擦角为φ,以上均为已知量.圆弧ABCD为一假定的滑动面,与地平线的交点为A、C,与坡顶的交点为D,过圆心O'作地表的垂线O'B,以交点O为原点,水平向和竖直向分别为X、Y坐标轴建立直角坐标系.圆心O'距C点和A点的水平距离均为a,坡脚F距C点的距离为l,半径O'A和半径O'C与Y轴的夹角均为α,在某一假定滑动面给定的情况下,a、α和l均为已知量.

考虑到在滑坡体范围域积分和在滑动面上线积分的方便,选取l、a和α为表示滑动面圆弧所在位置的自变量,上述3个参数可以唯一的确定一个圆.其余各参数均可由上述3个自变量表示如下：

以滑动面上部的滑坡体整体作为研究对象,其受力分析如图2所示.滑坡体受到自身重力G、下部土体对其的法向力(垂直于滑动面)和下部土体对其的抗剪力(与滑动面相切)共3个力的作用,滑坡体在这3个力的作用下应满足极限平衡条件.

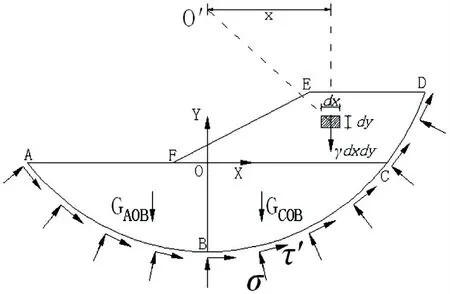
图2 均质土坡滑坡体受力分析示意图

1.1 滑动面上的平均剪应力

根据力矩平衡条件,3个力对圆心O'的力矩之和为零,即：

其中：1)法向力对圆心O'的力矩Mσ

滑动面上每点的法向力均过圆心,对圆心O'的力矩Mσ为零.

2)滑坡体自重对圆心O'的力矩MG

滑坡体自重对圆心O'的力矩MG为AOB、BOC和CDEF 3部分土体的重力对圆心O'的力矩之和.根据对称性,AOB和BOC两部分土体的重力对圆心O'的力矩大小相等、方向相反,则MG在数值上等于土体CDEF的重力对圆心O'的力矩.

在土体CDEF中取一微元体,如图2所示,该微元体重力的大小为γd x d y,方向为竖直向下,对圆心O'取矩的力臂长度为微元体的横坐标x,则在土体CDEF范围内进行二重积分可得滑坡体自重对圆心O'的力矩MG为：

3)抗剪力对圆心O'的力矩Mτ'

设滑动面上的平均剪应力为τ,其在数值上等于滑动面上实际发挥的平均抗剪应力τ'.则抗剪力对圆心O'的力矩Mτ'为：

将式(2)和式(3)代入式(1),解得滑动面上的平均剪应力τ为：

1.2 滑动面上的平均抗剪强度

根据库仑抗剪强度定律,滑动面上的平均抗剪强度τf与土的抗剪强度指标c、φ和滑动面上的平均正应力σ有关.由于滑动面上每点的正应力难以精确求解,目前的解法均需引入假设条件,条分法即是通过划分土条,并对条间力进行不同的假设,以求得各土条底部正应力的近似值,再求得各土条底部抗剪强度的近似值,最后再求出整个滑动面上平均抗剪强度的近似值.由于在严格满足极限平衡条件的情况下,安全系数对滑面底部正应力的分布并不敏感,对正应力进行合理的处理或假设,可得出合理的安全系数值[12],本文将滑动面上的平均正应力(待求解的未知量)设为σ,建立水平方向的静力平衡方程.由于滑坡体所受的3个力在X方向的分力之和为零,方程如下：

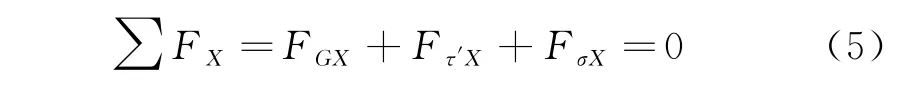
其中：1)滑坡体重力在X方向的分力FGX为零;2)抗剪力在X方向的分力为Fτ'X.

如图3所示,在滑动面上任取一角度为dη的微圆弧,微圆弧与圆心所连半径与Y轴的夹角为η,则该微圆弧上的抗剪力在X方向上的分力为τ'R·cosηdη,在整个滑动面范围内进行积分,得：

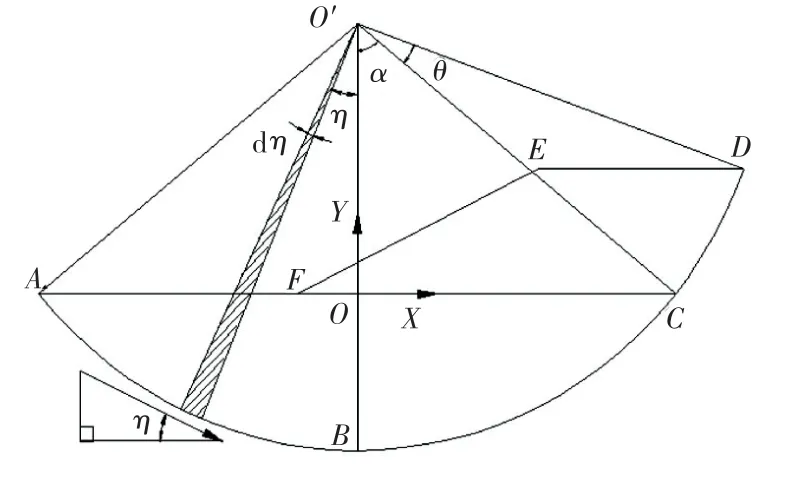
图3 抗剪力在X方向的分力示意图

3)法向力在X方向的分力FσX

如图4所示,在滑动面上任取一角度为dη的微圆弧,微圆弧与圆心所连半径与Y轴的夹角为η,则该微圆弧上的法向力在X方向上的分力为σR sinηdη,在整个滑动面范围内进行积分,考虑到圆弧和圆弧上的法向力在X方向上的分量大小相等、方向相反,得：

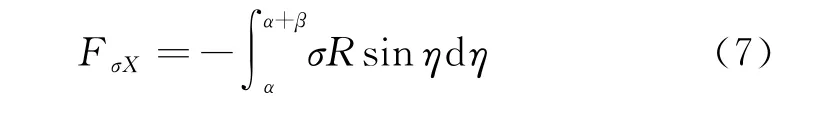
图4 法向力在X方向的分力示意图

将式(6)和式(7)代入式(5),解得滑动面上的平均正应力σ为：

将式(4)代入式(8),并根据库仑抗剪强度定律,得滑动面上的平均抗剪强度τf为：

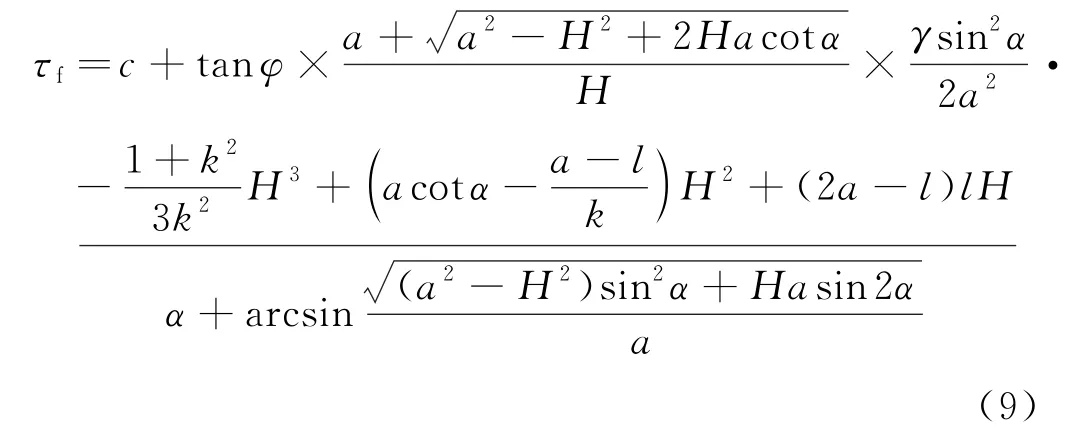
1.3 土坡的安全系数

土坡的安全系数定义为整个滑动面上的平均抗剪强度与平均剪应力之比[9-10],即：

将式(4)和式(9)代入式(10),解得土坡在该假定滑动面下的安全系数为：

2 均质地基土坡

根据库仑定律,求解滑动面上的平均抗剪强度τf需要求得滑动面上的平均正应力σ,本文即是先设定该待求解未知量,然后通过平衡方程直接求出该值.这种设法将导致在建立和求解平衡方程时,滑动面ABC上的正应力虽然已考虑在内,但实际上并未参与运算,在土坡自重的作用下,地表下ABC上的正应力应该比地表上CD上的正应力大,而且绝大多数人工边坡为均质地基土坡(如路堤、坝体等),地表上、下为两种不同的土体,其抗剪强度指标也不同,求解抗剪强度也应分开考虑.因此对于均质地基土坡,将滑动面分为ABC和CD两段,首先求出各段上的平均正应力,再求平均值得整个滑动面上的平均正应力σ及整个滑动面上的平均抗剪强度τf.

对于均质土坡,同瑞典法、Bishop法和陆军工程师团法一样,本文方法也仅采用了两个平衡方程,即：水平方向的静力平衡方程和力矩平衡方程.不同之处在于,本文方法未利用竖直方向的静力平衡方程,而瑞典法和Bishop法未利用水平方向的静力平衡方程,陆军工程师团法未利用力矩平衡方程.

对于均质地基土坡,由于两个方程仅能求解两个未知量,分两段考虑滑动面上的正应力时,还应增加竖直方向上的静力平衡方程.

基于以上分析,同样以滑动面上部的滑坡体整体作为研究对象,不同点在于设滑动面CD和ABC上的平均正应力分别为σ1和σ2,其受力分析如图5所示.滑坡体受到自身重力G、下部土体对其的抗剪力(与滑动面相切)、滑动面CD上的法向力和滑动面ABC上的法向力(垂直于滑动面)共4个力的作用,滑坡体在这4个力的作用下应满足极限平衡条件.

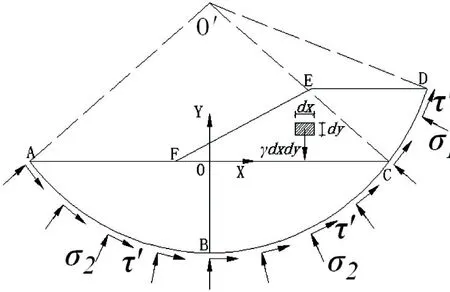
图5 均质地基土坡滑坡体受力分析示意图

2.1 滑动面上的平均剪应力

根据力矩平衡条件,4个力对圆心O'的力矩之和为零,与均质土坡类似,建立力矩平衡方程,由于σ1和σ2对圆心O'的力矩仍然均为零,故滑动面上的平均剪应力τ仍为式(4),此处不再赘述.

2.2 滑动面上的平均抗剪强度

根据水平方向的静力平衡条件,滑坡体所受的4个力在X方向的分力之和为零,考虑到重力G和滑动面ABC上的法向力在X方向的分力均为零,建立水平方向的静力平衡方程为：

根据竖直方向的静力平衡条件,滑坡体所受的4个力在Y方向的分力之和为零,建立竖直方向的静力平衡方程如下：

其中：

1)抗剪力在Y方向的分力Fτ'Y

参考图3,在滑动面上任取一角度为dη的微圆弧,在整个滑动面范围内进行积分,得：

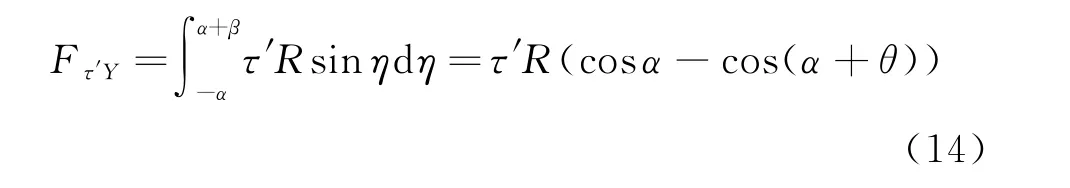
2)滑动面CD上的法向力在Y方向的分力Fσ1Y

在滑动面CD上任取一角度为dη的微圆弧(示意图略),在滑动面CD范围内进行积分,得：

在滑动面ABC上任取一角度为dη的微圆弧(示意图略),在滑动面ABC范围内进行积分,得：

4)滑坡体重力在Y方向的分力FGY

如图5所示,滑坡体的重力由ABC和CDEF两部分土体的重力组成,即：

ⓐABC部分土体的面积可由扇形O'ABC与三角形O'AC的面积之差得到如下：

ⓑ如图5所示,在土体CDEF中取微元体d x d y,在面积CDEF上范围内进行二重积分,得CDEF部分土体的面积为：

将式(18)、式(19)代入式(17),得滑坡体重力在Y方向的分力FGY为：

将式(4)、式(12)、式(14)～式(16)、式(20)代入式(13),解得滑动面ABC上的平均正应力σ2为：

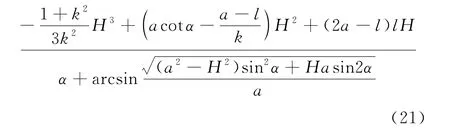
则滑动面CD和滑动面ABC上的平均抗剪强度τf1、τf2为：

2.3 土坡的安全系数

将式(4)、式(23)代入式(10),即可推导出土坡在该假定滑动面下的安全系数公式：

3 算例验证

利用Mathematic编制了上述所有变量的代码以及全过程的计算程序,限于篇幅,相关代码此处不做介绍.本节通过一个算例给出该方法的计算过程和结果,并与4种条分法的结果进行了对比.

算例选取由卢廷浩主编,河海大学出版社出版的《土力学》一书中的例题7-2,例题示意图参见此书,此处略.已知条件为：土坡高度H=15 m,坡率k=0.5,土容重γ=19.5 k N/m3,土黏聚力c=40 k Pa,内摩擦角φ=8°,假定滑动面的圆心坐标为(20,-10.08),半径为27 m,换算到图1中的直角坐标系得a=10 m,l=20 m,α=arctan(10/25.08)=0.379 4,根据上述已知条件,书中例题采用瑞典条分法计算(土条划分为10个),得出对应该假定滑动面的土坡安全系数为1.43.

该算例为均质土坡,此处首先采用均质土坡的公式(11)计算,再采用均质地基土坡公式(24)计算(视为特殊情况下均质地基土坡),简称为例1、例2.

例1的计算过程和结果见表1.计算过程中有部分中间计算参量未在表中列出,如θ=0.8088.

表1 例1的计算过程和结果

例2的计算过程和结果见表2.计算过程中有部分中间计算参量未在表中列出,如θ=0.8088,SCDEF=218.966 m2.

表2 例2的计算过程和结果

不同条分法的计算结果不同,而且即使对于同一种条分法,土条个数不同,求出的安全系数也有差别.作为对比,本文用简化Bishop法、陆军工程师团法、Spencer法和Morgenstern-Price法4种条分法分别求出算例的结果,为统一精度,土条个数均取10个(与书中瑞典法求解的土条划分个数相同),限于篇幅,具体的计算过程此处不再列出,将4种条分法的结果与例1、例2和瑞典法的结果共同列于表3.

表3 不同方法求解的算例稳定安全系数

由表3可见：本文方法计算均质土坡所得稳定安全系数略保守(例1),由于不同条分法的假设条件不同,计算的土条底部正应力也不同,其数值越小,滑动面上的平均抗剪强度也越小,得出的安全系数也就越偏于保守(越小).文献[13]也证明了在边坡均质且无指向坡外的外加水平荷载的条件下,用瑞典法、简化毕肖普法、斯宾塞法、陆军工程师团法和传递系数法计算同一个滑面为圆弧形的边坡稳定系数时,瑞典法的结果最小,表3的结果与其是一致的.本文方法在ABC上的正应力虽然在建立方程中已考虑,但实际上并未参与运算,所以求出的整个滑动面上的正应力偏小.

本文方法计算均质地基土坡精度较高(例2),各法所得安全系数很接近,进一步验证了满足平衡条件下,所得的安全系数对滑面正应力分布不甚敏感,可见本文设平均正应力和平均切应力的方法是可取的,文献[13]指出对于同一算例,满足力和力矩平衡条件的3个平衡方程求出的安全系数基本相同,偏差一般不大于5%.本文方法和严格条分法的Spencer法、Morgenstern-Price法的精度很接近,偏差在0.68%.

4 与条分法对比的几点讨论

4.1 关于假设条件的讨论

对于条分法而言,由于划分土条后未知数的个数大于二维条件下平衡方程的个数,所以必须要引入假设条件才可求解.假设条件的引入,直接目的是为了求解各个土条底部的正应力,最终目的是为了求解整个滑动面上的平均抗剪强度.

对于本文方法,为了求解整个滑动面上的平均正应力,首先设该值为一未知数(均质土坡),或将该值分为两部分,分别设各部分为一未知数(均质地基土坡),然后通过平衡方程直接求出该值.所以本文方法不需引入条间力的假设条件,相比条分法而言有其优越性.

4.2 关于求解精度的讨论

对于条分法而言,求解精度与两个方面有关：一是土条划分的数量,二是所作的假设条件.土条数量越多,假设越接近于实际,其精度越高,由于本文方法并未划分土条,故以下仅讨论假设条件引起的精度问题.由于做了假设,所以得到的各土条底部的正应力均为近似值,最终得到的整个滑动面上的平均抗剪强度和土坡的安全系数也均为近似值,只是假设条件越接近于实际情况,其精度越高而已.

对于本文提出的方法,求解精度与滑动面分段考虑正应力的段数有关,也即与设置正应力未知数的个数有关,滑动面分段越多(设置的未知数个数越多),求解精度越高.均质土坡将整个滑动面作为一段,设置了一个未知数,加上滑动面上的平均剪应力共有2个未知数,用两个平衡方程即可解出;均质地基土坡根据实际受力情况,将整个滑动面分成地表以上和地表以下两部分,设置了两个未知数,加上滑动面上的平均剪应力共3个未知数,故需增加一个竖直方向上的静力平衡方程才能求解.若为了提高精度增加分段个数,必须引入假设条件才能求解,但如此也就失去了本文方法的初衷,且由于引入了假设条件,其精度也未必提高.若想更进一步地提高精度,可在三维空间下建立严格的6个平衡方程来求解,但工程中遇到的边坡稳定性问题大多为平面应力问题(如路堤边坡等),所以三维空间下更进一步的精确求解也无必要.

4.3 关于工程应用的讨论

对于均质土坡而言,从计算精度上来说,宜将其视为特殊情况下的均质地基土坡进行计算,从工程实践来说,也可采用式(11)进行计算,简便且偏于保守.

对于均质地基土坡而言,由于采用了3个平衡方程,且根据实际情况分段求解了滑动面上的正应力,加之未引入条间力的假设条件,精度较高.

5 结 论

本文针对均质土坡及均质地基土坡,提出了一种非条分法的稳定安全系数新算法.通过引入描述圆弧滑动面的三个自变量,基于极限平衡原理,以滑动体整体为研究对象并以其为积分域,建立积分形式的平衡方程,推导出稳定安全系数的函数表达式,通过计算机编程后极大提高了计算效率,安全系数具有唯一性且具有较高的精度,可作为一种安全系数新的求解方法.

1)在严格满足极限平衡条件时,安全系数对滑面正应力分布不甚敏感,对正应力进行合理的处理或假设,以潜在滑动体为研究对象进行整体极限平衡分析,可得出合理的安全系数值.

2)算例结果表明,与传统条分法相比,采用本文方法计算的均质土坡所得稳定安全系数略显保守.

3)算例结果表明,与传统条分法相比,采用本文方法计算的均质地基土坡精度较高,与Spencer法、Morgenstern-Price法的计算偏差为0.68%.

4)在工程应用中,对于均质土坡而言,可直接采用本文方法计算,但从计算精度上来说,宜将其视为特殊情况下的均质地基土坡计算.