风载作用下高空贝雷架支撑系统的稳定性分析
2020-09-18田清伟丁胜勇郑保敬
田清伟 丁胜勇 郑保敬
(1.中国长江三峡集团有限公司, 北京 100038;2.三峡大学 水利与环境学院, 湖北 宜昌 443002)
升船机作为一种船舶过坝设备,相比船闸具有节水、过坝速度快等优点,目前在国内外已被广泛采用,如三峡升船机、向家坝升船机、尼德芬诺升船机、吕内堡升船机等[1].为适应快速提高的通航需求,目前升船机提升扬程正向着200 m以上特大型方向发展.升船机塔柱在施工过程中,其顶部横梁结构具有跨度和高度大、施工载荷大、支撑结构受力大,施工环境复杂,施工安全风险大等技术特点.其中,在横梁施工混凝土结构自身强度尚未形成时,需要其模板支撑结构承受施工时的各种载荷,包括结构自身的重力、施工载荷和风载荷等等.该模板支撑结构不同于普通的脚手架,它们搭设跨度大,搭设高度高,需承受施工载荷大,属于超高大跨承受重载的支撑体系,是升船机土建工程建设中的重点和难点工程项目之一[2-3].贝雷架支撑系统作为优选方案在三峡升船机建设中首次得到成功应用[4],研究其施工过程中贝雷架的强度、刚度和稳定性对今后类似工程的建设具有重要的指导作用.
目前,关于贝雷架结构强度和刚度的研究已非常成熟,其评估方法基本可以从各种设计手册中查到,但贝雷架结构的稳定性仍是国内外学者们关注的研究领域[5-6].在设计三峡升船机贝雷架结构时,由于受到试验条件和试验场地的限制,物模试验主要通过预压对局部贝雷架梁的安全性进行了验证[7].考虑实际工况中,贝雷架被架设在180 m左右的高空,且今后会向更高的架设高程发展,贝雷架支撑体系所受到的横向风力载荷不容忽视,显然地面试验的方式无法反映出贝雷架在高空真实的受力情况.贝雷架梁作为横梁混凝土浇筑施工模板系统的高空支撑“地基”,一旦发生失稳现象,将会对工程造成巨大经济损失,甚至造成重大人员伤亡,因此,研究风载荷作用下的高空贝雷架支撑体系的稳定性问题是必要的.
本文以三峡升船机为例,研究风载荷对塔柱顶部横梁贝雷架支撑体系稳定性的影响,并考虑结构大变形时的几何非线性,通过数值方法计算贝雷架屈曲的失稳模态和临界载荷,为贝雷架在类似高空复杂施工环境中的设计研究和实践应用提供理论参考.
1 非线性稳定性分析
1.1 非线性稳定性分析的有限元理论
考虑几何非线性时,贝雷架结构稳定分析增量形式的有限元平衡方程为[8]:
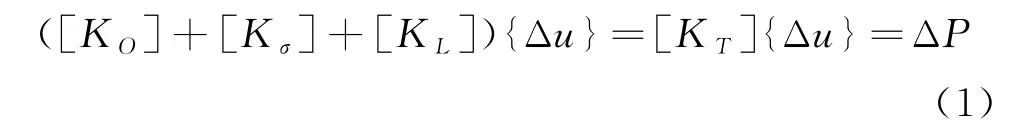
式中:[KO]=∫[BO]T[D][BO]d V,[Kσ]=∫[BL]T·{σ}d V,[KL]=∫([BO]T[D][BL]+[BL]T[D][BL]+[BL]T[D][BO])d V,{σ}=[D]({ε}-{ε0})+{σ0};[KO]为结构的线弹性刚度矩阵;[Kσ]为结构的切应力刚度矩阵;[KL]为结构的初位移矩阵;[KT]为结构的切线刚度矩阵;ΔP为载荷增量;[BO]为线性应变分析的矩阵项;[BL]为位移列阵{u}的线性函数;[D]为材料的线弹性矩阵;{ε0}、{σ0}分别为初应变、初应力列阵.
1.2 非线性稳定方程的求解方法
由于几何非线性的影响,用线性方法很难求解出(1)式中的{Δu},因此通常采用数值方法把非线性方程转化为一系列的线性方程来求解.常用的求解非线性屈曲问题的方法有直接迭代法[9]、Newton-Raphson方法[10]和弧长法[11]等.对于贝雷架支撑体系存在完全崩溃或者突然变换到另一种稳定形态的结构非线性屈曲问题,其物理意义上是属于不稳定系统,目前应用较多的是Newton-Raphson法,又称N-R法.对于非线性方程组式(1)采用N-R法时可得到如下迭代形式:

若{Δδi+1}={δi+1}-{δi}小到满足求解精度要求时停止迭代,δi+1即为近似解.
1.3 非线性稳定性分析的有限元过程
利用ANSYS有限元软件对贝雷架结构进行稳定性分析时,其非线性屈曲分析的计算流程如图1所示.

图1 ANSYS非线性屈曲分析的计算流程图
2 计算模型
2.1 工程概况
三峡升船机船厢室段为塔柱结构,在塔柱顶部高程196 m处左、右两侧由11根跨航槽横梁和2个平台连接,其结构如图2所示.上部横梁和平台在浇筑过程中首次采用了贝雷架+钢管排架支撑方案.因混凝土梁尺寸、重量不等,各贝雷架梁所需承受的载荷也不一样.对应横梁、纵梁、基础梁及观光平台不同区域,贝雷架梁形式分为单层、单层顶部加强型、双层顶部加强型、双层上下加强型4种形式,具体布置如图3所示.
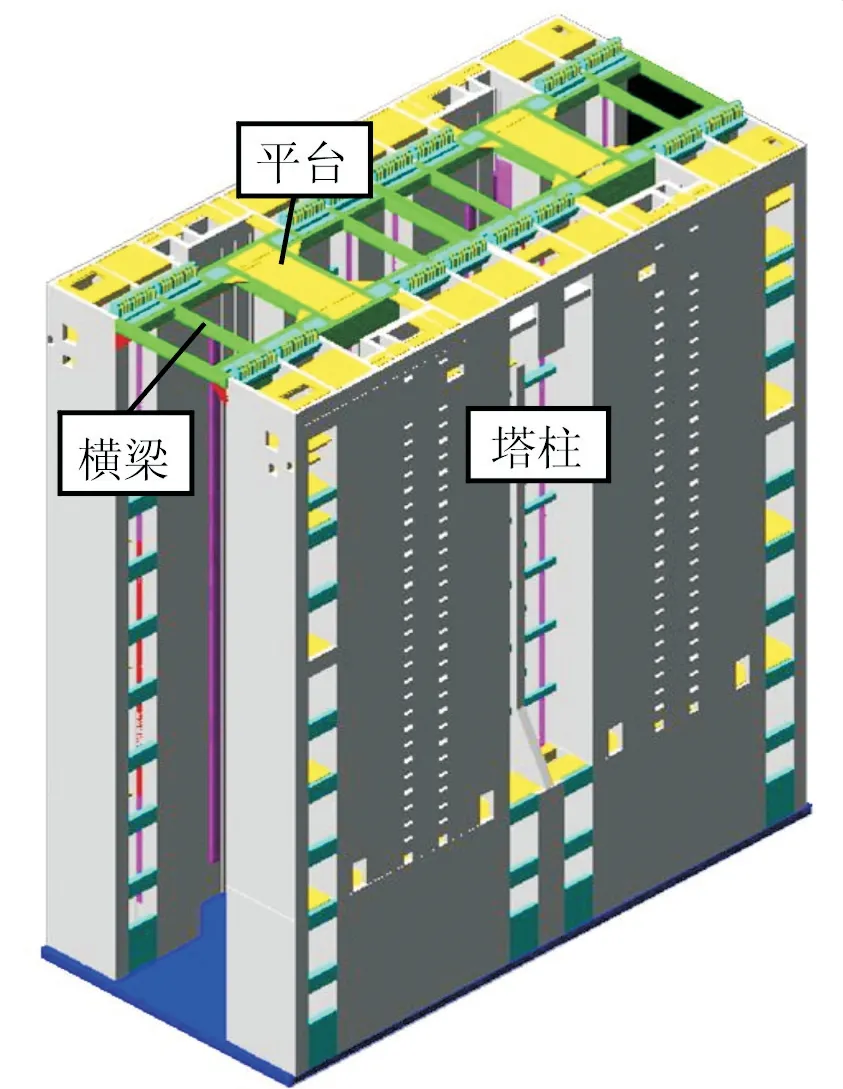
图2 三峡升船机顶部横梁梁系结构图
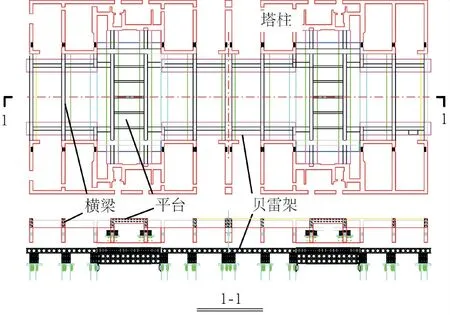
图3 贝雷架布置图
为了便于后文表述,根据贝雷架分布情况和受力特点,本文将整个贝雷架支撑体系划分为上游区域、中部区域、下游区域和2个平台共5个区域.
2.2 网格模型和边界条件
根据三峡升船机的设计图纸和施工方案,采用ANSYS有限元软件建立贝雷架支撑体系整体有限元网格模型,如图4所示.贝雷架标准片各杆件采用Beam189梁单元模拟,整个计算模型包含124 454个单元和57386个节点.利用笛卡尔坐标系建立整体分析坐标系,其中,X轴正向为下游指向上游方向;Y轴正向为坝体右岸指向左岸方向;Z轴方向为重力反方向.
整个贝雷架支撑体系分成上下两层,上层贝雷架直接架设在下层贝雷架上,而下层贝雷架梁则是依靠两端安装在钢牛腿上的钢箱梁来支撑的.因此,可仅对下层贝雷架梁进行简支约束处理,对左端支撑点施加X、Y、Z 3个方向的位移约束,对右端支撑点施加Y、Z两个方向的位移约束.
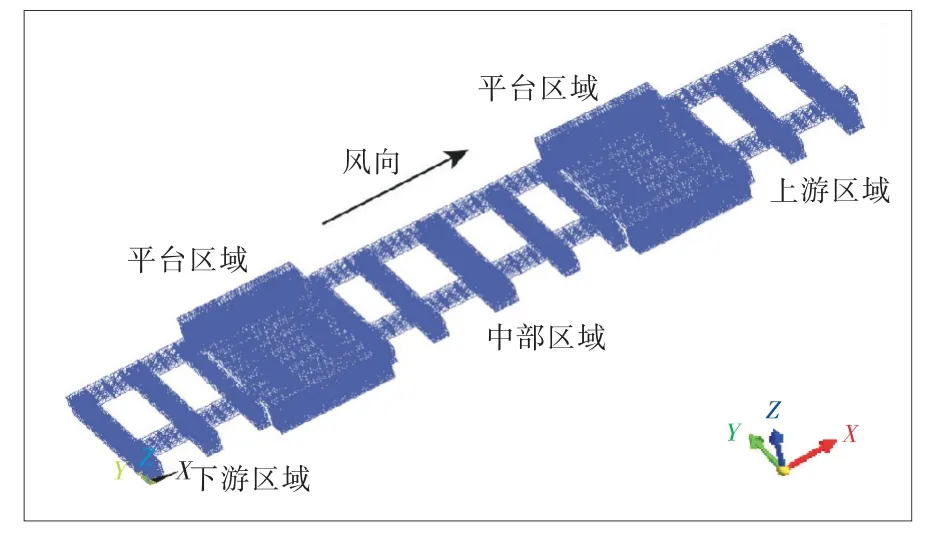
图4 贝雷架支撑体系网格模型
2.3 载荷计算
作为支撑体系,贝雷架结构除了承受自身的重力外,在施工过程中还需承担上部排架、模板系统、塔柱顶部混凝土梁板等结构的重量,以及施工人员和施工器械产生的施工载荷.同时,贝雷架架设的高度在180 m左右,风载对支撑体系的影响也应加以考虑.具体的计算载荷包含:
1)载荷1:贝雷架自身重力.
贝雷架密度取ρ=7 850 kg/m3,重力加速度g=9.8 m/s2.
2)载荷2:贝雷架施工期载荷.
由于不同区域对应的混凝土梁尺寸、重量不等,各个贝雷架梁承受的载荷也不一样.根据贝雷架结构的受力特点,可将所受施工期载荷转化为作用于贝雷架弦杆上的线载荷,具体计算情况如下:
(a)施工人员及机具载荷,取2.5 k N/m2;
(b)排架和模板系统,载荷值见表1;
(c)振捣混凝土产生的载荷,取2.0 k N/m2;
(d)浇筑混凝土梁、板载荷,取25 k N/m3.
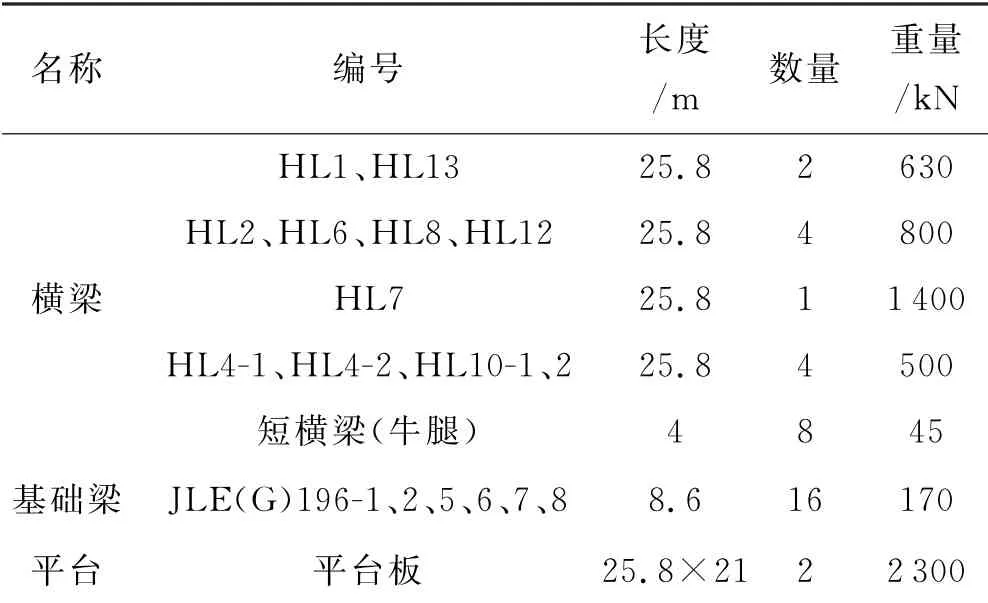
表1 排架和模板系统重量
3)载荷3:风载荷
假定风向从下游水平吹向上游,贝雷架及其上部排架、模板系统都将受到水平风压作用.这里将排架和模板系统的风载荷传递到贝雷架的作用效果简化为施加于对应贝雷架上的水平力和弯矩,如图5所示.最后,根据贝雷架结构的受力特点,将所受风载荷转化为作用于弦杆上的线载荷分配到各个贝雷架.
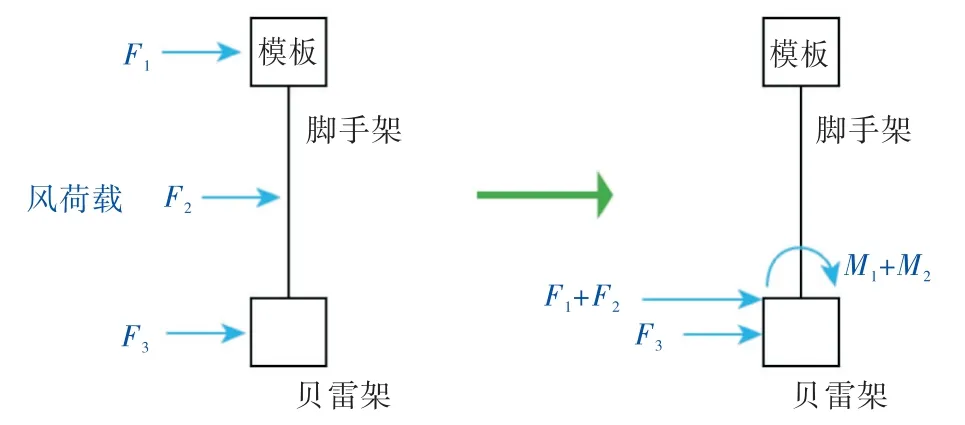
图5 风载荷等效加载示意图
根据《起重机设计手册》相关之规定[12],风载荷计算式采用:

其中:C为风力系数;Kh为风力高度变化系数;A为迎风面积;q为基础风压.风力系数C=1.3(贝雷架、排架)和1.4(模板);风力高度变化系数Kh=2.25;根据三峡大坝当地气候资料显示,平均最大风速约为七级风,则基础风压为182 Pa.
3 计算分析
3.1 特征值屈曲分析
为了方便研究贝雷架的稳定性,将贝雷架的自重和施工期载荷之和作为恒载Ph,七级风载荷作为单倍活载PH.正常求得贝雷架的屈曲临界载荷应该为Pcr=λ×(Ph+PH),其中λ为特征值屈曲稳定系数.在ANSYS中对贝雷架进行特征值屈曲分析时,对活载荷进行缩放,并不断调整活载放大系数X进行加载分析,直到计算得到的屈曲载荷系数为1且第一阶屈曲模态保持不变为止.
实际计算时,令初始活载放大系数X=1,计算得到的屈曲载荷系数λ,将λ和X的乘积作为下一次的放大系数,不断重复这个过程直到最后计算得到的屈曲载荷系数λ=1为止.此时,屈曲载荷系数与活载放大系数X的乘积基本保持不变,所加的载荷也就是贝雷架的屈曲临界载荷.
按照上述方法对贝雷架结构不断调整活载荷系数进行屈曲分析,并提取一阶屈曲模态,记录屈曲载荷系数λ与活载荷放大系数X的变化过程如图6~9所示.由于上、下游和中部区域贝雷架结构采用了近似的主次梁布置方式,从图中可以看出其屈曲载荷系数λ收敛情况基本一致.

图6 上游特征屈曲极限载荷与活载荷倍数的关系曲线
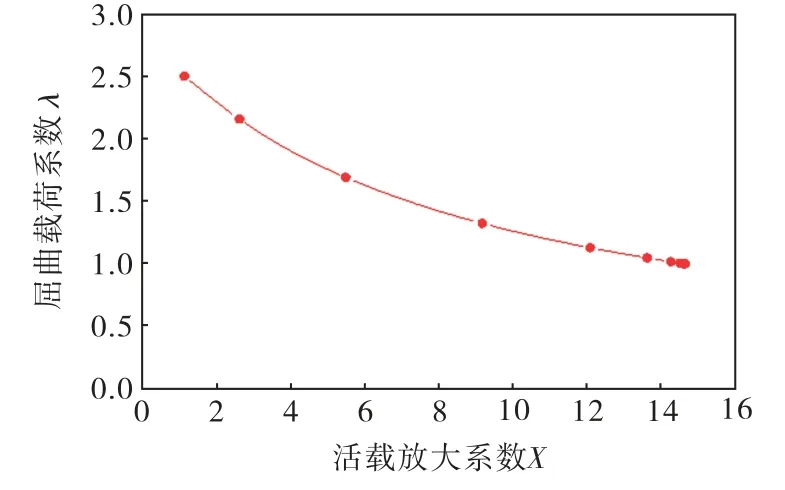
图7 下游特征屈曲极限载荷与活载荷倍数的关系曲线
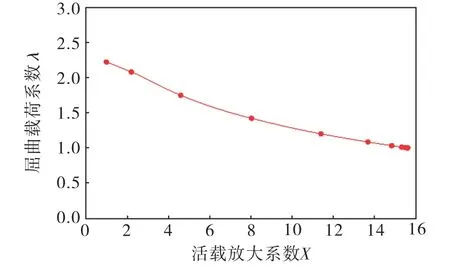
图8 中部区域特征屈曲极限载荷与活载荷倍数的关系曲线

图9 平台特征屈曲极限载荷与活载荷倍数的关系曲线
当贝雷架结构取屈曲临界载荷时,各区域对应的一阶屈曲模态如图10~13所示(局部放大区域为发生失稳部位).从图中可以看出不同区域贝雷架最易发生的都是下层贝雷架两端支座位置附近的局部杆件失稳,由于不同区域的支撑体系都是包含多根贝雷架梁的组合结构,屈曲分析中并未出现单贝雷架梁最易发生的跨中侧弯失稳.作为支撑体系中主承重梁的下层贝雷架梁,由上层贝雷架传递来的载荷存在偏心,其受力特性实质上是一个弯、剪、扭的复合受力问题,而风载荷的施加又会加大下层贝雷架梁沿横截面的扭转效果,造成支座附近背风侧的贝雷架腹杆轴力偏大,因此,从图中结果可以看出,此处的杆件更容易发生屈曲失稳.

图10 上游区域贝雷架临界载荷1阶屈曲模态

图11 下游区域贝雷架临界载荷1阶屈曲模态

图12 中部区域贝雷架临界载荷1阶屈曲模态

图13 平台区域贝雷架临界载荷1阶屈曲模态
3.2 非线性屈曲分析
在考虑初始缺陷对结构极限载荷的影响程度时,应用“一致缺陷模态法”,先对结构进行线性屈曲模态分析,以结构的一阶模态作为初始缺陷的分布模态引入结构,并通过一定的比例因子确定初始缺陷的大小.为了获得准确的结构极限载荷,可选择一阶失稳模态位移最大节点作为观测点绘制载荷-位移曲线并判断是否收敛,一般以第一个临界点处的载荷值作为结构的极限载荷.通过采用不同比例因子计算发现,初始缺陷大小的改变对最终的屈曲极限载荷影响较小,因此由贝雷片组装而成的贝雷架并不是对缺陷敏感的桁架结构.若以一阶模态变形值的1%作为初始缺陷的大小,不同区域采用对应的一阶失稳模态位移最大节点作为观测点,得到的载荷-位移曲线结果如图14~17所示.
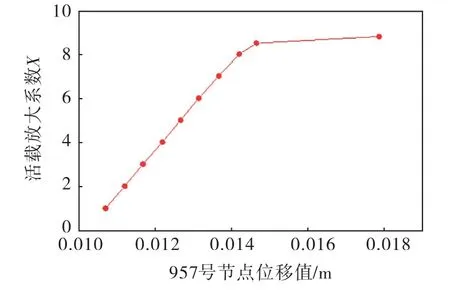
图14 上游区域贝雷架节点957号处的载荷-位移曲线

图15 下游区域贝雷架节点12346号处的载荷-位移曲线
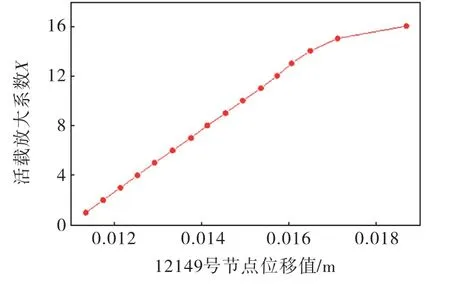
图16 中部区域贝雷架节点12149号处的载荷-位移曲线

图17 平台区域贝雷架节点60578号处的载荷-位移曲线
从图中可以看出,上游区域贝雷架在活载放大系数达到8倍左右时,节点957的位移值迅速增大而不再受到载荷的线性控制;下游区域贝雷架在活载放大系数达到14倍左右时,节点12346的位移值迅速增大而不再受到载荷的线性控制;中部区域贝雷架在活载放大系数达到14倍左右时,节点12149的位移值迅速增大而不再受到载荷的线性控制;平台区域贝雷架在活载放大系数达到28倍左右时,节点60578的位移值迅速增大而不再受到载荷的线性控制.此时的载荷都造成了贝雷架结构发生了明显的失稳,即为贝雷架各个区域的极限屈曲载荷.
为了研究几何非线性对贝雷架稳定性的影响,将贝雷架的线性屈曲极限载荷和非线性屈曲极限载荷进行比较,见表2.

表2 贝雷架不同区域屈曲极限载荷对比(活载放大系数)
从表中可知,在考虑初始缺陷和几何非线性时,贝雷架上游区域和平台区域的屈曲极限载荷减小非常明显,而下游区域和中部区域的屈曲极限载荷有所减小,但幅度不大.由此可见,相较于下游区域和平台区域,上游区域和平台区域对缺陷敏感程度更高.
4 结 论
本文采用有限元数值方法,对风载作用下三峡升船机塔柱顶部横梁施工时贝雷架支撑体系的稳定性进行了分析,通过计算贝雷架支撑体系屈曲时的失稳模态和临界载荷,总结出以下结论:
1)在风载作用下,贝雷架支撑体系的上游、下游和中部区域下层贝雷架梁牛腿支座附近的背风侧杆件更容易发生局部失稳;而在平台区域下层贝雷架梁牛腿支座附近的船厢侧腹杆更容易发生局部失稳.因此,在核算贝雷架腹杆轴力时应注意考虑下层贝雷架梁所受载荷的偏心问题.
2)考虑初始缺陷的几何非线性对贝雷架结构上游区域和平台区域稳定性的影响更为明显,而对于下游区域和中部区域,贝雷架的失稳位置都发生在靠中间的贝雷架梁,当中间的贝雷架梁发生局部失稳后,偏外侧的贝雷架梁将会承担更多的载荷,整个结构体系仍未丧失承载能力.
