多边形比例边界有限元非线性高效分析方法

李佳龙，李 钢，余丁浩

(大连理工大学海岸和近海工程国家重点实验室，辽宁，大连 116024)

比例边界有限元法(Scaled boundary finite element method，简称SBFEM)是由Wolf 和Song[1−2]提出的一种半解析的数值求解方法，最早用于解决土-结构相互作用问题中的无限域动力刚度的计算[3]。多边形比例边界有限元法[4]结合了有限单元法与边界元法的优势，具有较高的计算精度以及收敛性[5]，目前已运用到众多工程问题的数值分析中[6−9]。多边形比例边界单元由于其网格的灵活性，在模拟裂纹扩展过程、处理局部网格重剖分等方面相较于有限元单元具有更明显的优势。目前，比例边界有限元法更多关注的是线弹性问题的求解，对于非线性问题的求解则研究较少。通过对多边形比例边界单元的弹性特性进行分析，可获得与有限单元法等价的形函数以及应变-位移矩阵，且对于线弹性问题与非线性问题均适用。基于此，Ooi 等[10]开创了多边形比例边界单元的非线性分析，并将其运用于弹塑性带裂纹问题的求解，其中单元的弹塑性本构矩阵采用最小二乘法进行数值拟合，但该方法计算过程复杂且要求多边形单元尺寸足够小才能够精确表达塑性区的变化。Chen等[11]提出在每个线单元覆盖的扇形区域引入3 个数值积分点来进行多边形比例边界单元的非线性分析，具有较高的计算精度。无论是Ooi 等[10]亦或是Chen[11]等所提出的多边形比例边界有限元非线性分析过程，两者的基本思路均是：先计算多边形比例边界单元的弹塑性刚度矩阵，然后再集成整个求解区域的总体刚度矩阵。然而，同传统有限单元法一样，均是对总体刚度矩阵进行分解求解从而获得单元的位移响应，但大规模刚度矩阵的分解依旧是限制非线性问题高效求解最主要的因素，因而有必要提出一种针对多边形比例边界单元的高效求解方法。

隔离非线性有限元法(Inelasticity-separated finite element method，简称IS-FEM)是由Li 和Yu[12]基于有限单元法的基本框架提出的一种结构非线性分析新方法，采用Woodbury 公式[13]直接求解控制方程，实现了局部非线性问题的高效求解。该方法将单元应变分解为线弹性应变与非线性应变两部分，非线性应变通过在单元中设置非线性应变插值点以插值的形式来表示，从而将结构的非线性部分隔离开来。对于非局部非线性问题，采用Woodbury 近似法[14−15]对控制方程进行求解，将非线性问题的迭代求解过程转换为多次的常刚度矩阵回代以及稀疏矩阵与向量的乘积，对大规模非线性问题的求解具有明显的效率优势。目前已成功运用于钢筋混凝土框架结构[16]、二维[17]以及三维[18]等问题的非线性分析，显示出其较高的计算效率。

本文将隔离非线性有限元法的思想用于比例边界有限元非线性分析，提出一种高效的隔离非线性比例边界有限元法(Inelasticity-separated scaled boundary finite element method，简称IS-SBFEM)。主要思想是：将多边形比例边界单元所有扇形区域独立考虑，在每个扇形单元内设置若干个非线性应变插值点，从而建立相互独立的非线性应变场。每个扇形区域的径向自然坐标以及环向自然坐标分别为ξ=[0,1]、η=[−1,1]，因此本文针对多边形比例边界单元的扇形区域提出一种新的数值积分方案，即：采用4 点高斯积分方案对线性的扇形子单元进行数值积分。对于更高阶的比例边界单元，选取更多的数值积分点进行数值积分即可获得足够的精度。该数值求解方案对于线弹性问题以及非线性问题均适用，且精度保持不变。由于隔离非线性比例边界单元相较于隔离非线性有限元单元引入了更多的非线性应变插值点，即便是局部非线性问题其舒尔补矩阵维数也往往较大，因此建议直接采用Woodbury 近似法对控制方程进行求解，但该方法对较小规模的非线性问题计算效率偏低。鉴于此，对于较小规模的非线性问题，建议采用多边形比例边界有限元法直接求解；对于大规模的非线性问题，采用隔离非线性比例边界有限元法求解具有更高的计算效率。基于MATLAB 平台分别编制了比例边界有限元法以及隔离非线性比例边界有限元法两套非线性分析程序，数值算例验证了本文所提出的隔离非线性比例边界有限元法的正确性与高效性。

1 SBFEM 基本理论

1.1 多边形比例边界有限元

在求解任意的平面问题时，可采用满足比例中心要求的多边形比例边界单元进行离散。图1为一典型的多边形比例边界单元，连接比例中心O与外边界线单元端部结点可将其划分为多个扇形子单元。边界线单元可采用一维线单元进行离散，其自然坐标为−1≤η≤1，因而边界线单元上的任意一点坐标(xb(η),yb(η))可表示为：

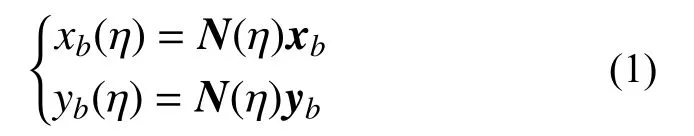
式中：xb=[x1,x2, ···,xm]T与yb=[y1,y2, ···,ym]T为该边界线单元上m个结点的坐标；N(η)为一维Gauss-Lobatto-Lagrange 形函数。

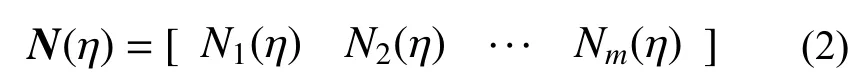
图1 多边形比例边界单元Fig. 1 Polygon scaled boundary element

在比例中心沿边界的径向方向引入自然坐标ξ，其坐标范围为0≤ξ≤1，其中：ξ=0 为比例中心位置，ξ=1 为边界位置。因而该求解域内任意点坐标(x(ξ,η),y(ξ,η))可表示为：

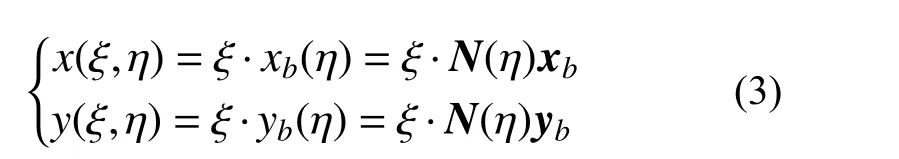
比例边界有限元法假定单元位移在环向方向为数值解，而在径向方向则为一解析解。将其在环向与径向两个方向上解耦，可表示为：

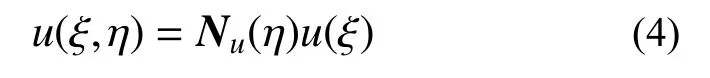
式中：Nu(η)为边界线单元的插值形函数；u(ξ)为径向方向的位移函数，u(ξ)的求解可参考比例边界有限元法相关文献[1 − 2，10 − 11]，此处不再赘述。通过对多边形比例边界单元的弹性特性进行分析，可获得每个扇形区与有限元单元等价的单元形函数Φ(ξ,η)以及应变-位移矩阵B(ξ,η)。两者仅与单元本身形状相关而与材料的性质无关，对线弹性问题以及非线性问题均适用，分别为：

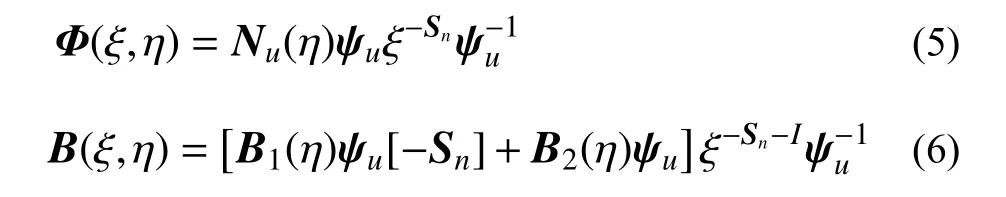
式中：ψu为位移模态对应的转换矩阵；Sn是由单元的Hamilton 矩阵的负特征值组成的对角矩阵；B1(η)与B2(η)为单元由笛卡尔坐标到局部坐标的转换矩阵。此时，单元的应变场ε(ξ,η)为：

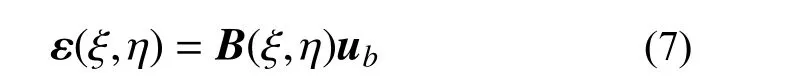
式中，ub为多边形比例边界单元的结点位移。

1.2 非线性比例边界有限元

比例边界有限元法作为一种基于位移的有限元求解方法，采用最小位能原理建立其非线性求解的控制方程。对于满足平衡条件的变形体结构有：

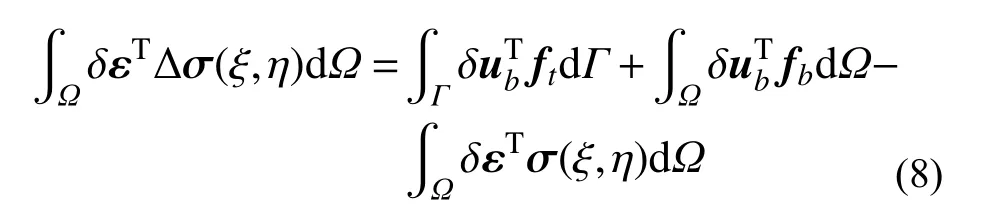
式中：ft与fb分别为单元边界载荷与体积载荷；σ(ξ,η)为单元上一个荷载步收敛后的应力；δε 为虚位移场δub对应的虚应变场，且有δε=B(ξ,η)δub。单元的应力增量Δσ(ξ,η)可通过单元的弹塑性矩阵Dep以及结点位移增量Δub表示为：

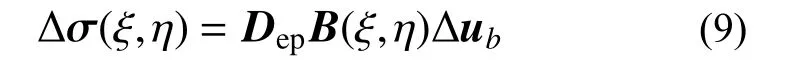
将式(5)、式(9)代入式(8)所示的虚功方程，即可得到多边形比例边界单元非线性求解的控制方程，即：

式中，kep、Δf分别为多边形比例边界单元的弹塑性刚度矩阵以及外荷载增量。

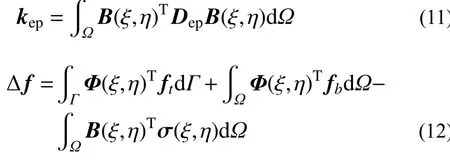
多边形比例边界单元的刚度矩阵kep与外荷载Δf的具体计算步骤为：首先，通过式(5)、式(6)获得多边形单元每一个扇形区的形函数Φ(ξ,η)以及应变-位移矩阵B(ξ,η)，然后，通过式(11)、式(12)计算该扇形区对单元刚度矩阵以及外荷载的贡献，最后，再集成该多边形单元的刚度矩阵以及外荷载向量[11]。通过对所有的多边形单元进行计算并按自由度组装获得计算域的总体刚度矩阵以及外荷载向量，即可得到整个计算域的控制方程：

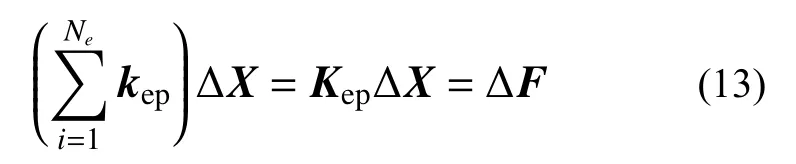
式中：Kep即为整个计算域的弹塑性刚度矩阵；ΔX与ΔF分别为总的结点位移增量与外荷载向量；Ne为整个计算域多边形单元个数。采用上述方法，可将半解析的比例边界有限元法转换成与有限单元法一样的纯数值求解方法，从而实现了多边形比例边界单元的非线性分析。

对于式(13)中的刚度矩阵Kep同样具有稀疏性，可采用LDLT分解法直接进行求解。然而，对于大规模问题的求解其计算效率偏低，因而有必要提出一种针对多边形比例边界单元的高效求解方法。

2 隔离非线性比例边界有限元法

2.1 应变分解与非线性应变插值

隔离非线性有限元法(IS-FEM)[12]作为一种高效的材料非线性分析方法，已在二维、三维等有限元问题中展现其较高的计算效率，在此将其推广至多边形比例边界单元的非线性分析，提出一种高效的隔离非线性比例边界有限元法(IS-SBFEM)。对于一个多边形比例边界单元，采用增量形式，每个扇形区域内任意点处的应变增量Δε(ξ,η)可通过该扇形区的应变矩阵B(ξ,η)以及单元边界结点位移增量Δub表示为：

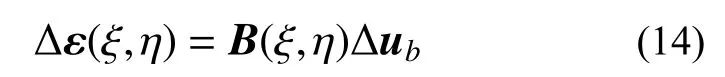
基于弹塑性力学的基本理论，单元内任意点处的应变增量Δε(ξ,η)均可分解为线弹性的应变增

2.2 控制方程

比例边界有限元法作为一种基于位移的有限元分析方法，采用虚功原理可建立隔离非线性比例边界有限元法的控制方程。

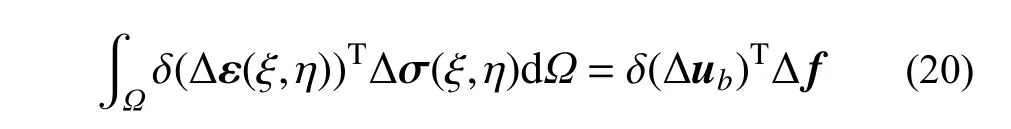
式中，δ(Δε(ξ,η))为虚结点位移δ(Δub)对应的虚应变，即：δ(Δε(ξ,η))=B(ξ,η)δ(Δub)。其中，虚应变δ(Δε(ξ,η))同样可以分解为虚线弹性应变δ(Δε′(ξ,η))以及虚非线性应变δ(Δε″(ξ,η))两部分，即δ(Δε(ξ,η)) =δ(Δε′(ξ,η)) + δ(Δε″(ξ,η))，且同样满足式(15)所示的非线性应变插值关系：δ(Δε″(ξ,η))=Csδ( ∆ε′s′)。将式(18)、式(19)两式所示的应力增量关系代入式(20)，即可得到隔离非线性比例边界单元的控制方程：

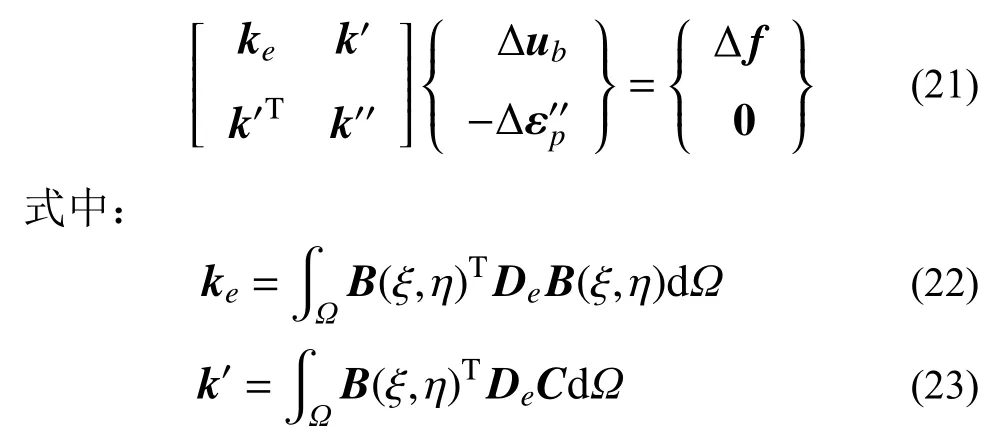
2.3 多边形单元数值积分

一个多边形单元可拆分为ns个扇形区域，因此，式(22)所示的多边形比例边界单元的刚度矩阵ke的计算过程为：先单独对每个扇形区域Ωs进行积分运算，然后再对所有的扇形区域进行集成。每个扇形子单元积分区域Ωs的自然坐标均为ξ=[0,1]与η=[−1,1]，且有dΩ=hξ|J(η)|dηdξ。因此，初始弹性刚度矩阵ke可表示为：

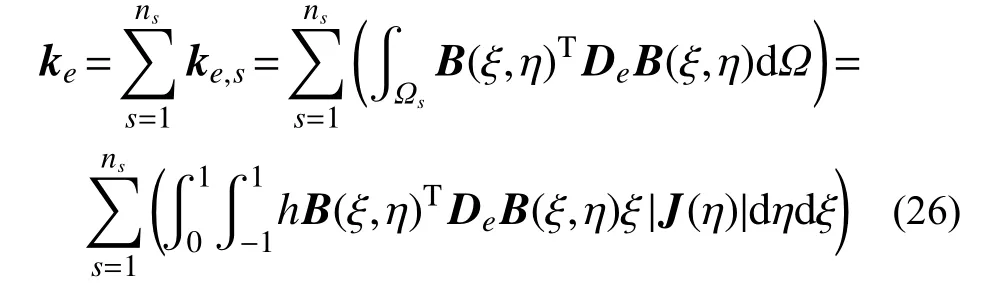
式中：ke,s为第s个扇形区域对整个多边形单元刚度的贡献；h为单元厚度；|J(η)|为边界线单元的雅克比矩阵。在扇形区域内引入g个高斯积分点，矩阵ke,s可采用高斯积分方案进行数值积分，有：

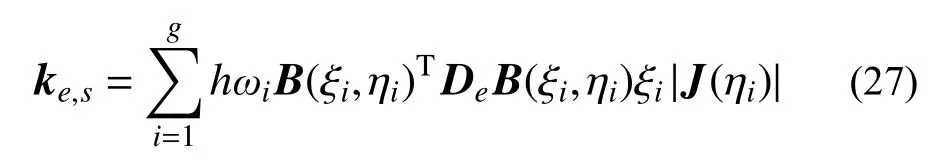
式中，ωi为积分权重。当多边形比例边界单元的阶数较低时，可采用表1 所示4 点高斯积分方案进行计算，图2 所示为多边形比例边界单元的数值积分点布置图，其中线单元上的高斯积分点仅用来计算多边形单元的形函数Φ(ξ,η)以及应变-位移矩阵B(ξ,η)。对于高阶的多边形比例边界单元，可设置更多的高斯积分点。

表1 扇形单元积分点坐标Table 1 Integral point coordinates of sector element

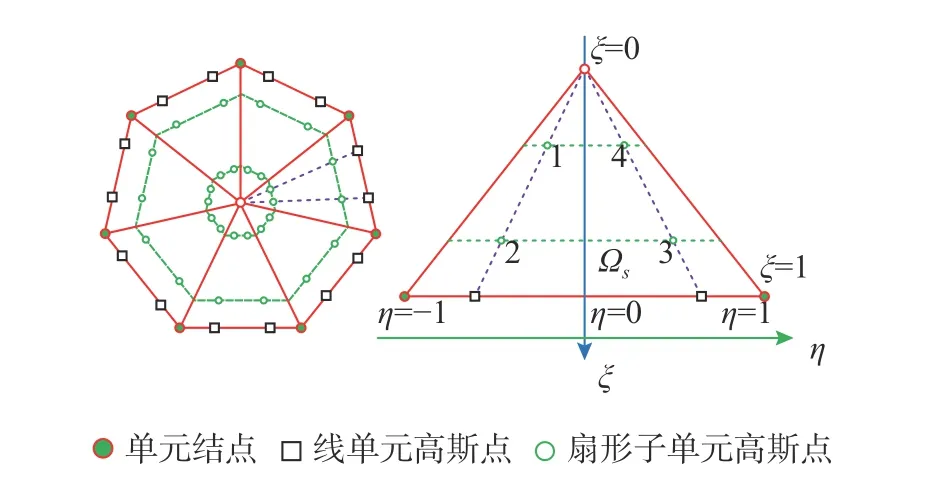
图2 多边形单元高斯点布置方案Fig. 2 Gaussian points layout scheme of polygon element

该积分方案对式(11)的计算同样适用，仅需将式(26)中的弹性矩阵De更换为弹塑性矩阵Dep，即可得到多边形比例边界单元的弹塑性刚度矩阵kep。多边形比例边界单元的弹塑性矩阵Dep的计算可直接调用有限元程序中的弹塑性矩阵计算模块，从而完成多边形比例边界单元的非线性分析。

式(23)与式(24)所示的单元矩阵k′以及k″的计算同式(22)一致，均是先通过高斯积分方案计算每个扇形区域的值，然后再进行集成。在对第s个扇形区进行数值积分时，由于假定每个扇形区域非线性应变场相互独立，则此时仅有该扇形区插值矩阵Cs存在，其余扇形区域的插值矩阵均为零矩阵。因而单元矩阵k′与k″是以扇形区为单元的分块矩阵以及分块对角矩阵。

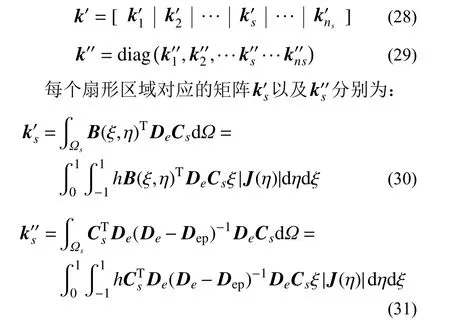
对于较低阶的比例边界单元，每个扇形区可采用图2 所示的4 个高斯积分点作为单元的非线性应变插值点。由于插值矩阵Cs为Kronecker delta 函数，因此式(30)、式(31)中的矩阵分别是以插值点为单位的分块矩阵以及分块对角矩阵。

其中，子矩阵分别为：

3 控制方程求解

对于一个ns边形的隔离非线性比例边界单元，其内部共有4ns个非线性应变插值点，因而其舒尔补矩阵KS规模较大，直接求解的计算量可能比传统的刚度矩阵直接分解求解的计算量还大。在此，可采用Woodbury 近似法[14−15](Woodbury approximation approach)对式(39)进行近似求解，整个求解过程仅为多次的常刚度矩阵回代以及稀疏矩阵与向量的乘积。该方法对于大规模非线性问题的求解具有明显优势，且规模越大其计算效率相对于直接的刚度矩阵分解求解算法效率更高。文献[17]已从理论上说明了对于平面有限元问题，当结点自由度数目超过2000 时即可体现出近似隔离非线性有限元法的高效性。

专职辅导员在专业知识和能力方面的缺乏，难以对学生做出专业的引导和相关职业的规划。培养专业辅导员既弥补了此方面的不足，又对专业课教师参与学生思政工作起到了抛砖引玉的作用。

基于本文所提出的隔离非线性比例边界有限元模型，编制了相应的计算程序，整体分析流程如图3 所示。

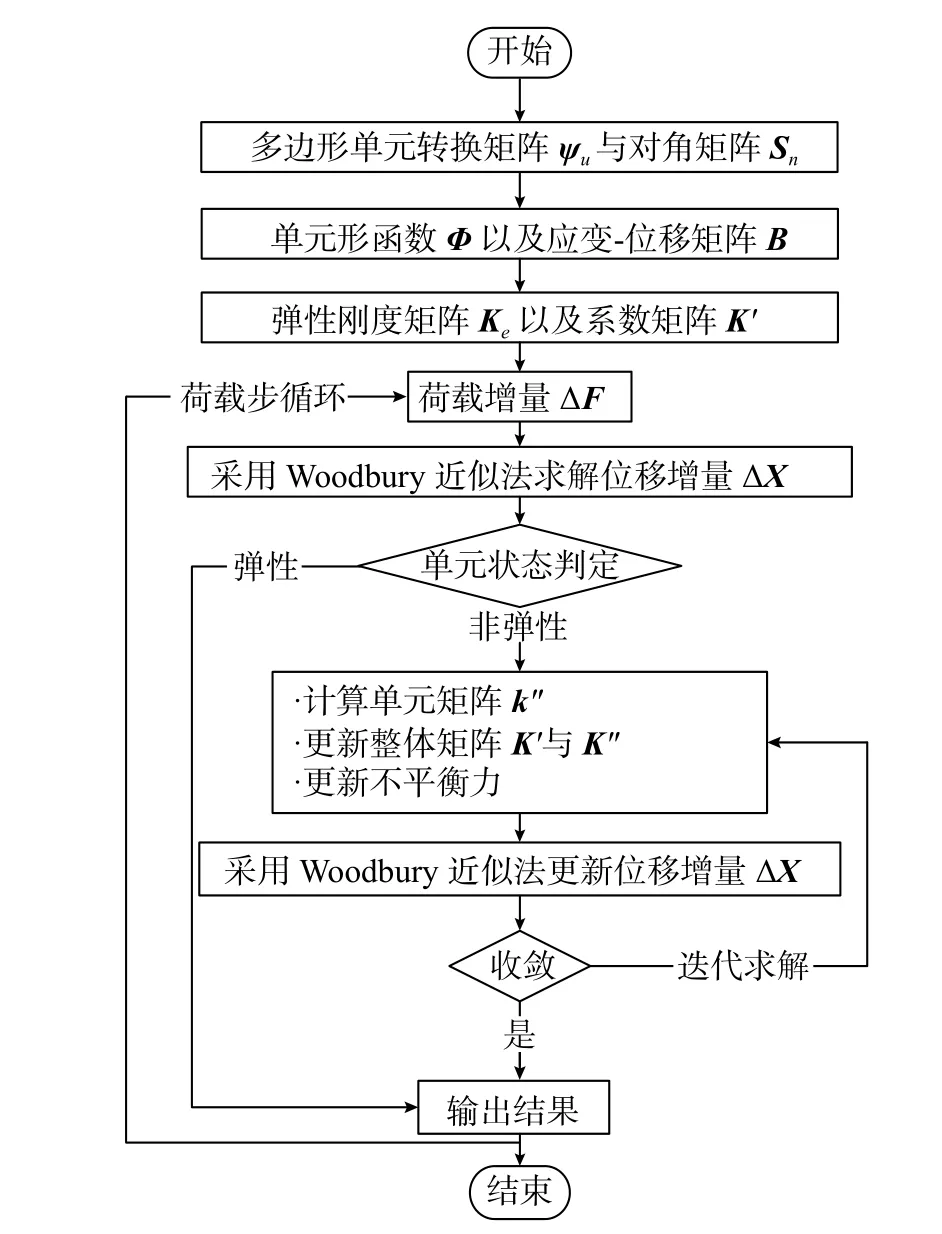
图3 隔离非线性比例边界有限元法分析流程Fig. 3 Analysis flow of IS-SBFEM

4 数值算例

4.1 悬臂梁静力分析

图4 为一悬臂梁模型，其几何尺寸如图所示，厚度为0.1 m。材料参数为：弹性模量E=2.0×105MPa，泊松比为ν=0.2。采用多边形网格以及线性四边形有限元单元进行网格剖分，其中多边形网格共计109 个单元以及264 个结点，如图5所示。有限元网格采用三种网格尺寸，分别为80 个单元与105 个结点、320 个单元与369 个结点以及1280 个单元与1377 个结点，分别如图6(a)、图6(b)以及图6(c)所示。

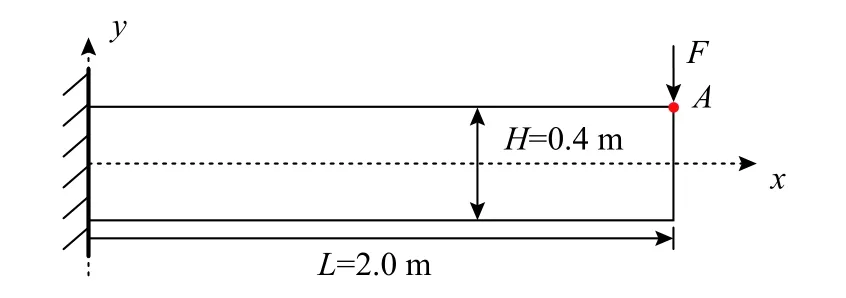
图4 悬臂梁模型Fig. 4 Cantilever beam model

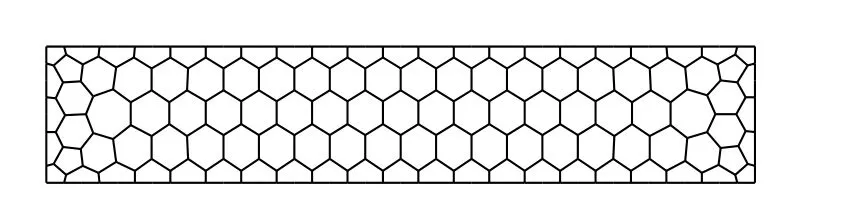
图5 多边形网格Fig. 5 Polygon mesh

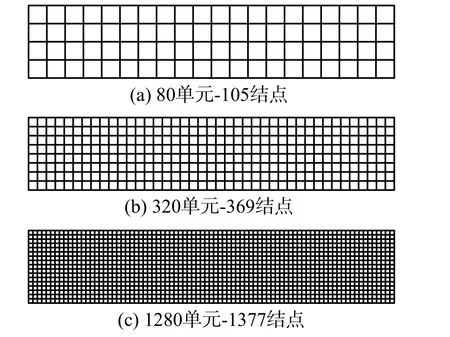
图6 有限元网格Fig. 6 Finite element mesh

4.1.1 弹性分析

在自由端结点A处施加竖向荷载F=100 kN，并假定网格最密的有限元模型c 为参考解。表2给出了结点A在不同网格模型下横向和竖向位移，可以看出采用本文提出的数值积分方案所得的计算结果与半解析的SBFEM 结果基本一致，且与有限元模型b 结果也基本一致。

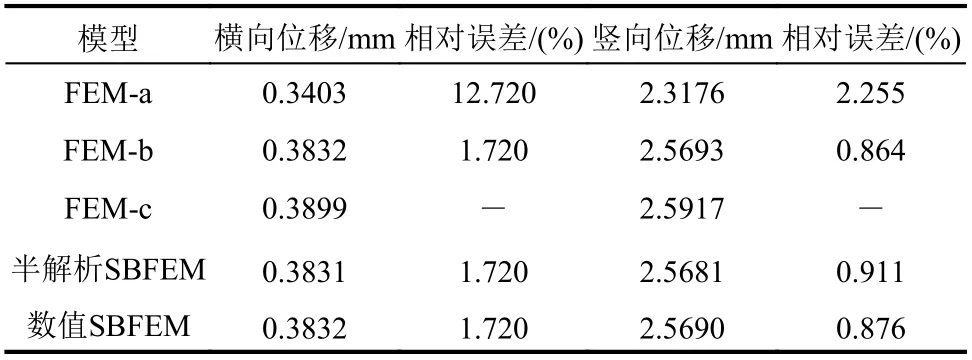
表2 A 点处的位移Table 2 Displacement of node A

4.1.2 弹塑性分析

假定该悬臂梁为双线性随动强化弹塑性模型，其初始屈服应力σy=360 MPa，切线模量Eh=0.002E。自由端结点A处施加往复竖向位移u，每个荷载步附加位移约束增量为d0=0.2 mm，共计2400 个荷载步[19]。采用SBFEM 以及IS-SBFEM两种求解方案，其中隔离非线性方案采用直接分解舒尔补矩阵的精确求解以及近似求解两种方法，共计四种求解方案。

通过弹性分析可知，有限元模型b 的刚度与多边形模型基本一致，因而选择模型b 作为对比模型来验证非线性分析的精度。图7 为两种网格模型结点A处的竖向荷载F与结点位移u的变化曲线，可以看出四种求解方案结果基本吻合，多边形单元的三种求解方案之间相对误差基本可以忽略。多边形模型与有限元模型计算结果一致，表明本文针对多边形比例边界单元所提出的数值积分方案以及IS-SBFEM 的正确性。图8 给出了IS-SBFEM 与SBFEM 两种求解方案的计算自由度曲线，比例边界有限元模型的刚度矩阵维数为510，而隔离非线性比例边界有限元模型的计算自由度随着非线性程度的增加与减少呈现高低变化。

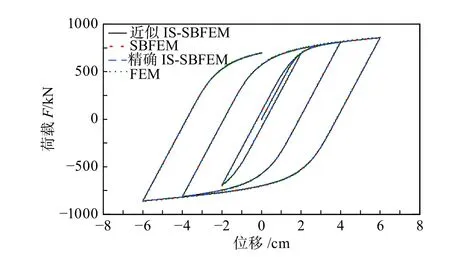
图7 竖向荷载-位移曲线Fig. 7 Curves of the vertical load vs. displacement

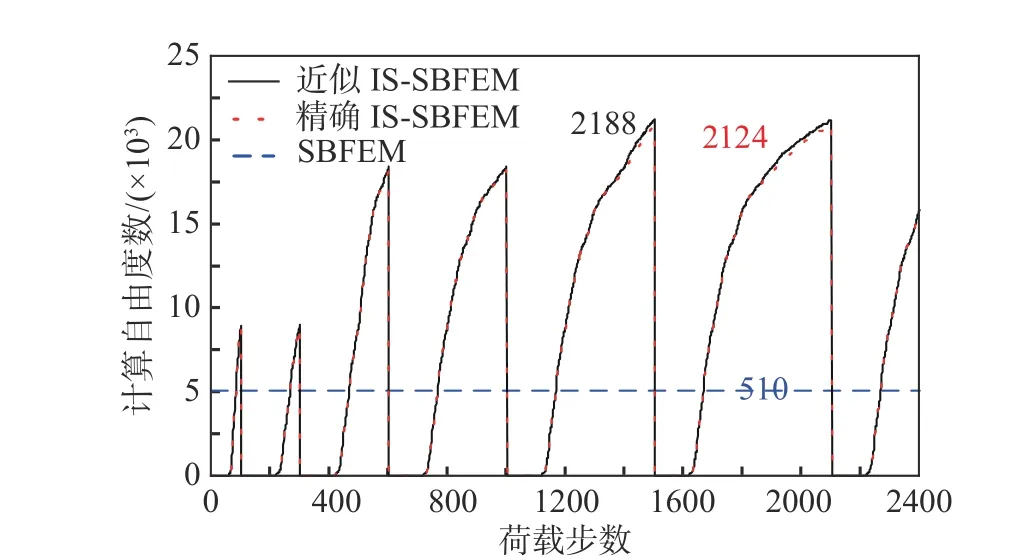
图8 计算自由度曲线Fig. 8 Calculate DOFs curves

表3 给出了多边形网格三种求解方案控制方程的具体求解时间，可以看出SBFEM 求解效率最高，近似IS-SBFEM 法次之，精确IS-SBFEM 最低。这是因为当问题规模较小时，刚度矩阵的分解与回代耗时两者差别不大，且仅需对刚度矩阵进行一次分解与回代即可得到当前迭代步的计算结果。近似的IS-SBFEM 由于要进行多次的常刚度矩阵回代以及稀疏矩阵与向量的乘积，因而其计算效率相对于直接的刚度矩阵分解法反而更低。采用精确的IS-SBFEM 进行求解时，由于舒尔补矩阵为高阶满阵且远大于刚度矩阵维数，因而其求解效率最低。

表3 控制方程计算时间Table 3 Calculate time of the governing equation

4.2 Koyna 重力坝动力非线性分析

印度Koyna 重力坝作为少数几个在强震中破坏且较有完整记录的重力坝之一，长期以来均被科研工作者奉为经典算例[20]。该坝长850 m，高103 m，符合平面应变模型几何特征，其具体几何尺寸如图9(a)所示。根据实际损伤以及相关文献可知，坝踵以及坡折面处均发生破坏，因而对这两处的网格进行局部加密，多边形有限元模型如图9(b)所示。其中坝踵以及坡折面处的网格细化图分别如图9(c)以及图9(d)所示，整个模型共计36904 个多边形单元以及18753 个结点。

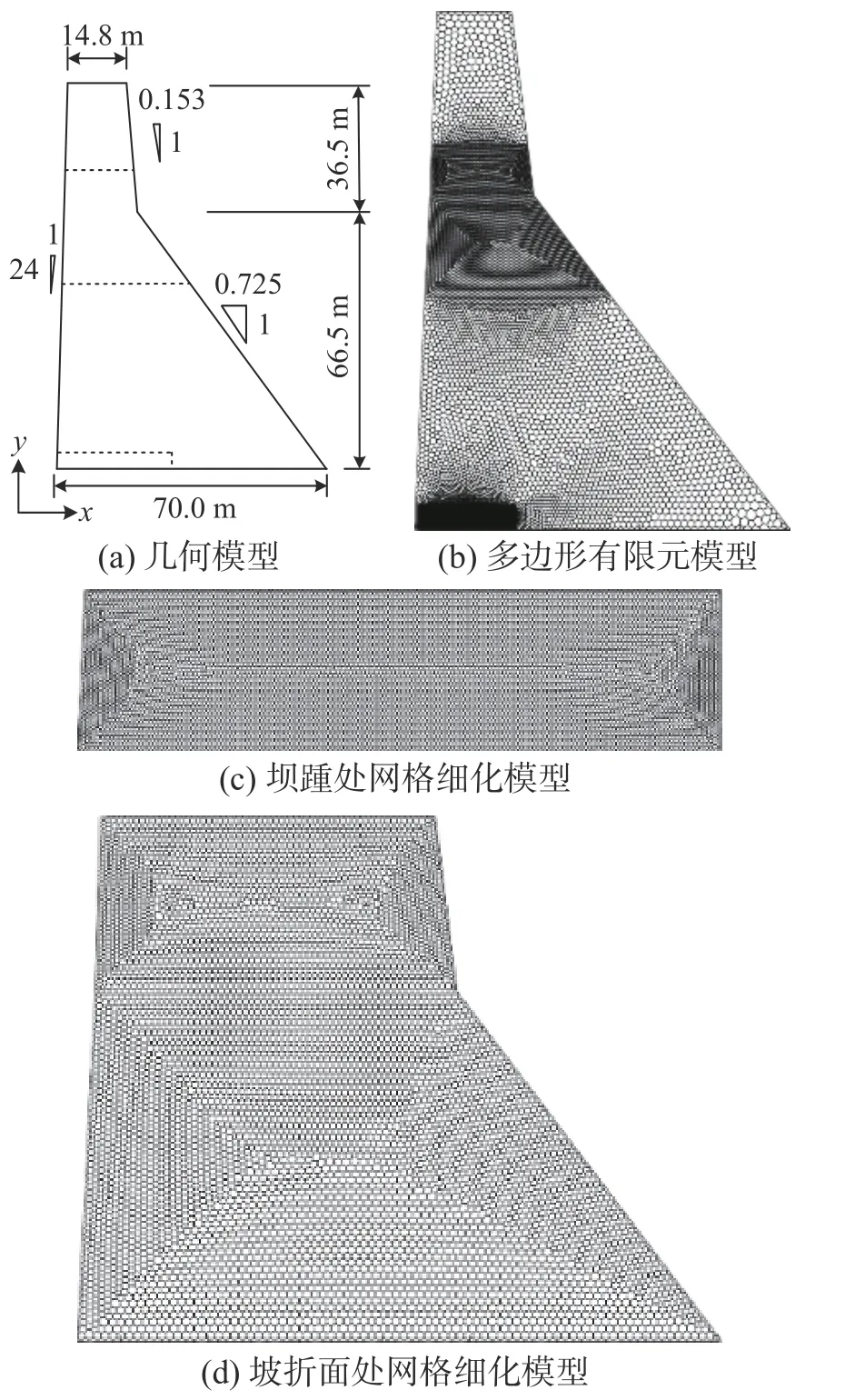
图9 几何模型与多边形网格Fig. 9 Geometry model and polygon mesh

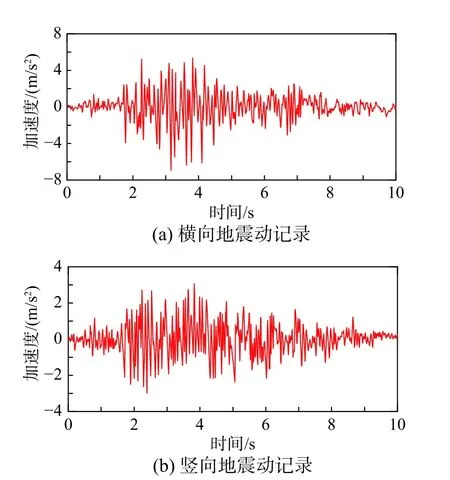
图10 Koyna 地震动记录Fig. 10 Seismic acceleration records of Koyna

图11～图16 分别为坝顶横向与竖向位移、速度以及加速度时程对比曲线。其中有限元模型采用线性四边形等参单元进行网格划分，整个计算区域共剖分103081 个结点以及102400 个单元。可以看出，FEM、SBFEM 以及IS-SBFEM 三种算法的计算结果完全吻合，再次验证了本文所提出的隔离非线性比例边界有限元法的正确性。

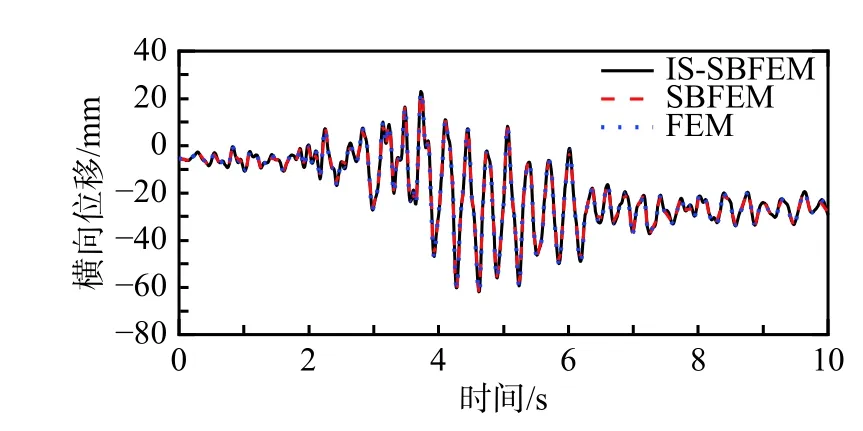
图11 坝顶横向位移反应Fig. 11 Horizontal displacement responses of dam crest

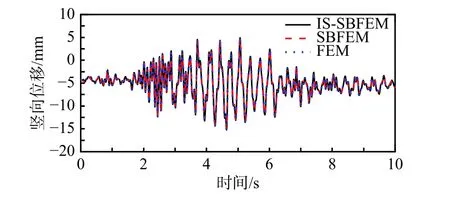
图12 坝顶竖向位移反应Fig. 12 Vertical displacement responses of dam crest

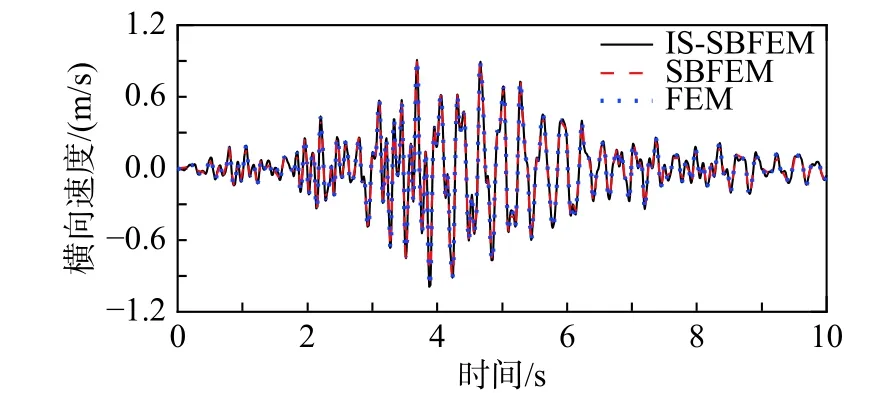
图13 坝顶横向速度反应Fig. 13 Horizontal velocity responses of dam crest

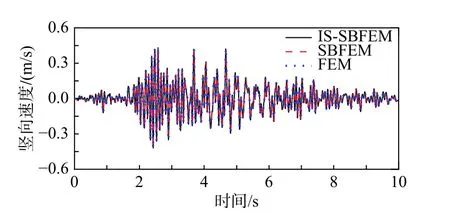
图14 坝顶竖向速度反应Fig. 14 Vertical velocity responses of dam crest

图17 给出了该重力坝模型计算自由度曲线，虽然部分荷载步的计算自由度大于刚度矩阵维数，但大多数荷载步的计算自由度却很小甚至模型仍处于弹性状态。

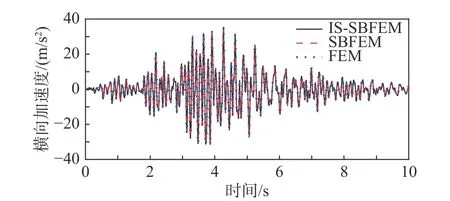
图15 坝顶横向加速度反应Fig. 15 Horizontal acceleration responses of dam crest

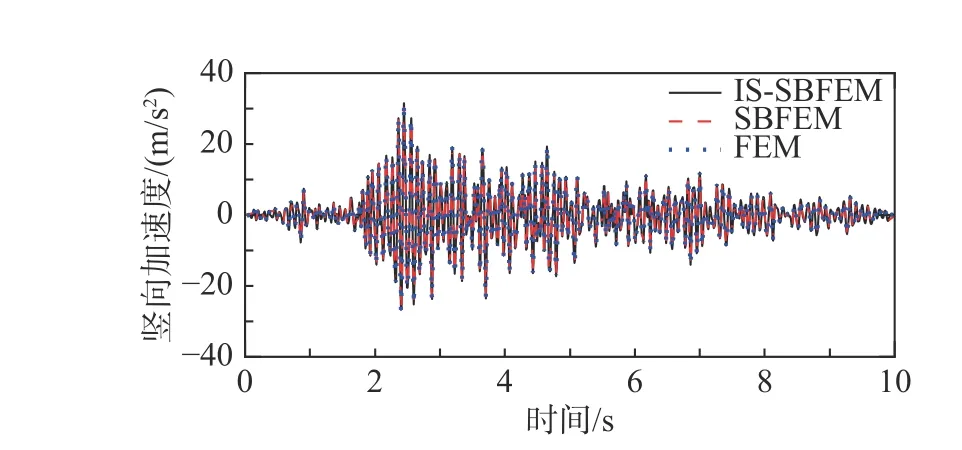
图16 坝顶横向加速度反应Fig. 16 Vertical acceleration responses of dam crest

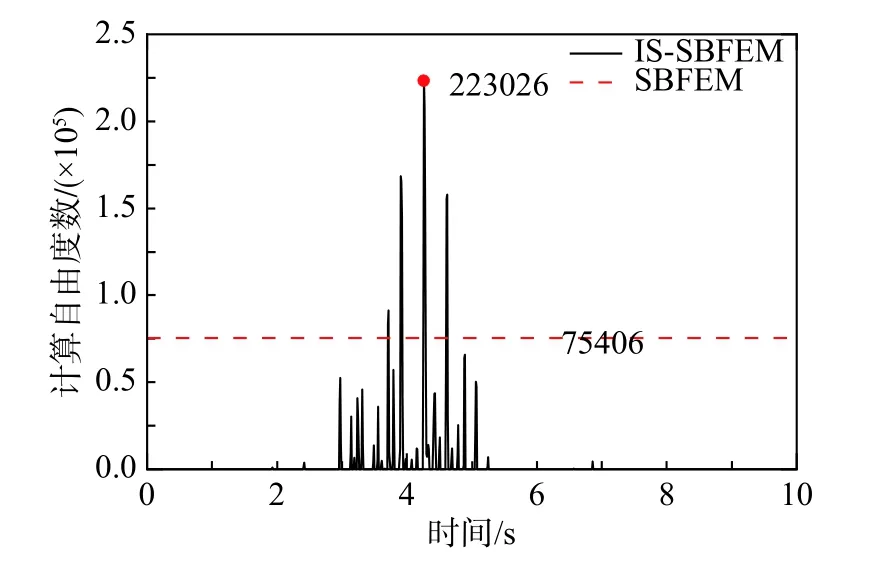
图17 计算自由度曲线Fig. 17 Calculate DOFs curves

表4 给出了两种比例边界有限元非线性分析方法控制方程的求解时间，可以看出SBFEM 的计算时间远大于近似IS-SBFEM 的计算时间，约为其7 倍。该多边形模型其刚度矩阵维数为75406，其一次分解与回代的计算时间分别约为1.8 s 与0.03 s。由于近似IS-SBFEM 的一次迭代过程仅为多次常刚度矩阵回代以及稀疏矩阵与向量的乘积，对于大规模非线性问题，采用IS-SBFEM 计算优势明显。由于存在高阶的舒尔补矩阵，精确的IS-SBFEM 不再适用。可见，对于大规模问题，IS-SBFEM 的计算效率远远大于SBFEM，此时ISSBFEM 应作为非线性分析的首选，既可在保证非线性计算精度的同时也具有极高的计算效率。

表4 控制方程计算时间Table 4 Calculate time of governing equation

5 结论

基于多边形比例边界有限元法基本理论，将隔离非线性思想用于多边形比例边界有限元非线性分析。在每个边界线单元覆盖的扇形区域内设置若干个非线性应变插值点，并以插值的形式建立其非线性应变场，从而构造了隔离非线性多边形比例边界单元。采用虚功原理建立了隔离非线性比例边界单元的控制方程，单元的弹塑性矩阵可直接调用有限元程序的本构模块获得，从而实现了多边形比例边界有限元高效非线性分析。得到如下结论：

(1)每个扇形区域其径向自然坐标以及环向自然坐标分别为ξ=[0,1]以及η=[−1,1]，可采用标准高斯积分方案进行数值积分，且对于高阶多边形比例边界单元也同样适用。

(2)多边形单元中引入较多的非线性应变插值点使得舒尔补矩阵维数较大，采用Woodbury 近似法联合算法对控制方程进行求解，可以保证隔离非线性比例边界有限元法的计算精度与高效性。

(3)对于大规模问题，建议采用隔离非线性比例边界有限元法进行分析，以便获得更高的计算效率。将该方法进行推广，对工程结构的非线性分析具有重要意义。