黏土蠕变非线性特性及其分数阶导数蠕变模型
2020-09-17任鹏,王鹏,张华,唐印
任 鹏,王 鹏,张 华,唐 印
(1. 四川省建筑科学研究院有限公司,成都 610081;2. 地质灾害防治与地质环境保护国家重点实验室(成都理工大学),成都 610059;3. 成都大学建筑与土木工程学院,成都 610106)
黏土的蠕变具有显著的非线性,尤其是在中-高应力条件下[1]。元件模型因为具有理论基础完善、形式简单、规律明确、概念清晰等优点,成为研究非线性蠕变的重要基础。目前非线性蠕变研究主要有以下几方面:1)传统元件与经验模型,孙均[1]提出采用传统元件模型描述低应力条件下的蠕变,非线性经验模型描述高应力条件下的蠕变,以此建立非线性蠕变模型;2)传统元件与新型非线性元件,李晶晶等[2]通过在Burgers 模型的基础上串联一个非线性黏塑性元件来描述加速蠕变,建立了膨胀土的非线性蠕变模型;刘开云等[3]通过构建应变触发式非线性黏滞元件来描述加速蠕变,并与Bingham 模型串联,建立了三维非线性蠕变模型;韩阳等[4]通过构建一种非线性黏滞元件,分别替换Burgers 模型中的两个黏滞元件,建立了非定常Burgers 蠕变模型;3)传统元件与损伤非线性元件,蒲成志等[5]基于损伤理论分别构建了弹性损伤元件和黏性损伤元件,并以此与其他经典元件组合建立了五元件非线性蠕变损伤模型;谢星等[6]采用Maxwell 模型和滑块元件并联描述线性蠕变,构建的损伤元件描述非线性蠕变,以此建立了统计损伤蠕变模型;4)传统元件与分数阶黏滞元件,郭佳奇等[7]通过分数阶微积分理论,构建了分数阶黏滞元件,并利用新元件代替Kelvin-Voigt 模型中的传统黏滞元件,建立了分数阶微积分Kelvin-Voigt 模型;肖世武等[8]通过采用Koeller 弹滞元件代替标准线性固体模型中的传统黏滞元件,建立了分数阶非线性流变模型;苏腾等[9]在Scott-Blair 分数阶元件和变系数分数阶元件的基础上,建立了变阶分数阶非线性黏弹塑性蠕变模型。国外对非线性蠕变也有大量的研究,Chunlin[10]通过Bingham 模型和Kelvin 模型,结合损伤理论,建立了非线性黏弹塑性损伤蠕变模型;Zhu 等[11]根据试验拟合,构建非线性化蠕变系数,并建立了非线性蠕变模型;Cao 等[12]基于损伤理论构建了一个损伤黏滞元件和损伤弹性元件,分别替换Burgers 模型中的传统黏滞元件和弹性元件,建立了非线性损伤蠕变模型;Li 等[13]基于分数阶微积分理论构建了分数阶黏滞元件,并将其替换了西元模型中的两个传统黏滞元件,同时还基于指数函数构建了非线性黏塑性元件,将其与改进西元模型串联,建立了非线性蠕变模型;Zhao 等[14]认为在蠕变过程中,弹性模量随应力或时间的变化非线性软化,而黏滞系数随应力或时间的变化非线性硬化,并基于损伤理论、硬化理论和Burgers 模型,建立了损伤硬化非线性蠕变模型。Yang 等[15]基于损伤理论和分数阶微积分理论,构建了分数阶黏滞元件,建立了五元件非线性损伤蠕变模型。非线性蠕变的研究已经硕果累累,但是也存在以下问题:经验模型理论基础不足、地域性限制大;基于新型非线性元件、损伤理论和分数阶微积分理论的蠕变模型常常因为建模元件数量较多,而引起模型参数多、形式复杂,不利于使用和推广。因此建立一个理论基础完善、形式简单、概念清晰的非线性蠕变模型是非常有必要的。
本文以成都黏土为研究背景,首先展开蠕变试验,通过分析黏土长期弹性模量和黏滞系数随应力和时间变化的规律,明确黏土蠕变的非线性规律;其次,基于分数阶微积分理论构建了分数阶导数元件,基于Harris 衰减函数分别构建了非线性软化弹性元件和非线性硬化黏滞元件,并建立了非线性分数阶导数蠕变模型;最后通过非线性蠕变模型的拟合验证分析,明确了本文蠕变模型的科学合理性。
1 蠕变试验
1.1 试验仪器
以成都黏土作为研究对象,进行三轴蠕变试验,其主要物理性质参数如表1 所示。由该黏土的液塑限及含水率计算可知,天然状态下的成都黏土处于硬塑状态,其黏聚力和内摩擦角相对较大,表明土体力学性质相对较好。但根据成都黏土地区的实际工程经验,成都黏土一般具有较强的水敏性及弱-中膨胀势,其综合力学性质复杂多变,其土体力学性质特殊性较强,具有一定的代表性。试验仪器采用CSS-2901TS 土体三轴流变试验机,如图1 所示,该试验仪器可通过应力控制的方式完成蠕变试验。

图1 CSS-2901TS 土体三轴流变试验机Fig. 1 CSS-2901TS soil triaxial rheological testing machine

表1 成都黏土的基本物理性质Table 1 Basic properties of Chengdu clay
1.2 试验方法
1)制样,试样尺寸为:高78 mm,直径39.1 mm,并采用抽真空注水的方法饱和试样。
2)装样及固结,对试样施加200 kPa 的围压,加压速率为0.1 kPa/min。当围压加压完毕后,先关闭孔隙水压力排水阀门,待孔隙水压力上升至围压的98%以后,打开孔隙水压力排水阀门,孔隙水压力逐渐降低,直至孔隙水压力消散达到95%以上,再次关闭孔隙水压力阀门,若稳定的孔隙水压力消散仍在95%以上,即认为试样固结完成。
3)蠕变加载方案,蠕变试验采用分级加载进行,加载总应力qf为333.98 kPa(qf根据《土工试验方法标准》(GB/T 50123−2019),由同等条件下的常规固结不排水三轴剪切试验确定)。每级轴向加载偏应力∆q=qf/x,x为加载级数(x=4);综上,本次蠕变试验的加载方案为:83.49 kPa→166.98 kPa→250.47 kPa→333.96 kPa。
4)蠕变试验每级荷载下的试样稳定标准为变形量小于0.01 mm/2d。
2 试验结果及分析
2.1 蠕变试验曲线
成都黏土的蠕变时程曲线如图2 所示。由图2可知,成都黏土蠕变有以下特点:前三级加载时,轴向应变随时间逐渐衰减,表现出衰减蠕变性质;第四级加载后,轴向应变先以稳定的速率变形,随后应变速率迅速增大,直至试样破坏,蠕变表现出一定的稳态蠕变和显著的加速蠕变性质。
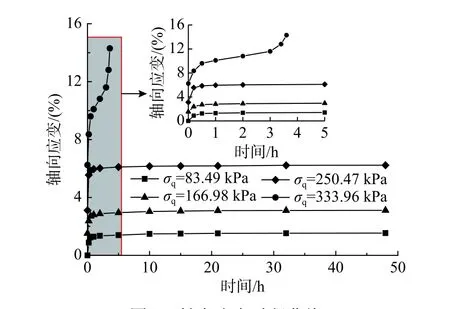
图2 轴向应变时程曲线Fig. 2 Time history curves of the axial strain
2.2 长期强度
成都黏土的等时应力-应变曲线如图3 所示。由图3 可知:应力应变等时曲线出现分离,随着时间的发展,加载瞬时的黏土应变远小于其他时刻的应变,表现出显著的蠕变变形。

图3 应力-应变等时曲线Fig. 3 Isochronous stress-strain curves
其原因可能为:黏土加载的瞬时速率远大于蠕变速率,土体力学性质表现出远大于长期弹性模量和长期强度的瞬时弹性模量和瞬时强度,因此加载瞬时的黏土变形较小;但在恒定荷载下,随着时间的增加,黏土力学性质表现出长期弹性模量和长期强度,其变形迅速增加,因此加载瞬时和加载后的应力应变曲线分离。第三级加载后,曲线出现拐点,根据沈明荣等[16]提出确定长期强度的等时曲线法,可将第三级轴向应力作为黏土的长期强度 σL;由于第四级轴向应力为常规三轴固结不排水确定的应力,其剪切应变速率远大于蠕变速率,可认为黏土是“瞬时”剪切破坏的,可将第四级轴向应力作为黏土的瞬时强度。
2.3 长期弹性模量
成都黏土弹性模量EL的时程曲线如图4 所示。由图4 可知:在前三级加载时,EL随着时间的增加先以较大的速率迅速衰减,随后逐渐收敛,保持不变;最后一级加载后,EL先以某一速率稳定衰减,随后衰减速率突增,直至土体破坏;并且EL随着应力的增加而减小;综上所述,EL是时间和应力的函数,随时间和应力的增加非线性软化。

图4 长期弹性模量时程曲线Fig. 4 Time history curves of the long-term modulus
2.4 黏滞系数
成都黏土黏滞系数 η的时程曲线如图5 所示。由图5 可知: η随着时间的增加而增加,随着加载应力的增大而减小;在最后一级加载时, η先随时间的增加而增加,但随后急剧减小,直至土样破坏。综上所述, η是时间和应力的函数,随时间的增加非线性硬化,随应力的增加非线性软化。
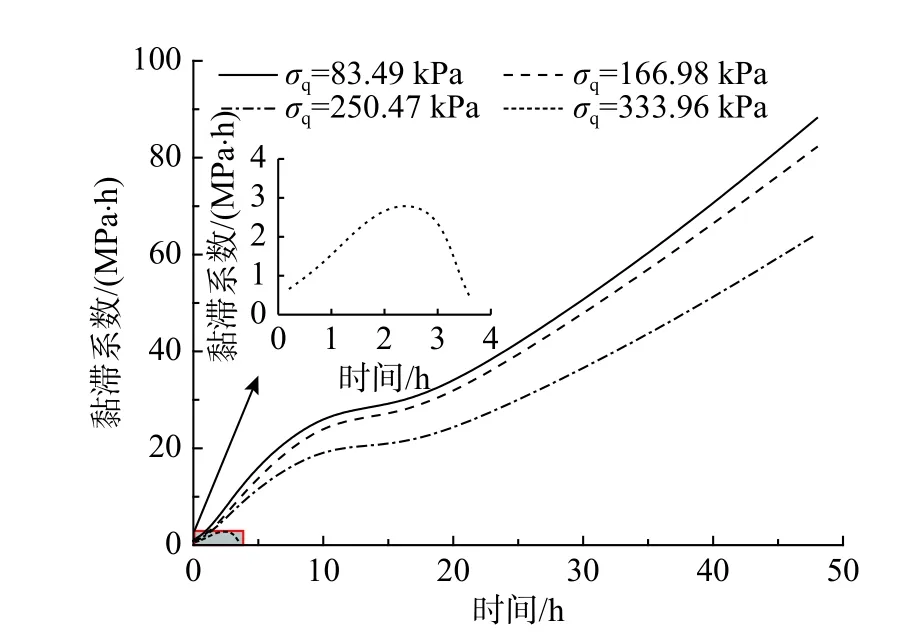
图5 黏滞系数时程曲线Fig. 5 Time history curves of the viscous coefficient
3 非线性蠕变模型
3.1 分数阶黏滞元件
元件模型虽然具有诸多优点,但其对非线性性质的描述还存在不足,而分数阶算子因为对材料的历史具有记忆性,在描述黏塑性和黏弹性时具有显著的优势,可很好地弥补元件模型的不足[17 − 18]。
分数阶微积分定义最常用的理论是Riemann-Liouville[19 − 20]理论:设函数f在(0,+∞)上连续可积,对t>0 , Re(n)≥0,分数阶积分有:
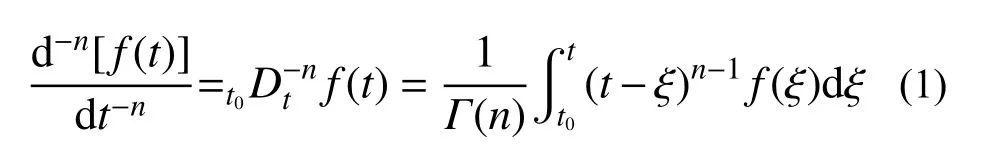
式中: Γ(n)为Gamma 函数;n为分数阶阶数。


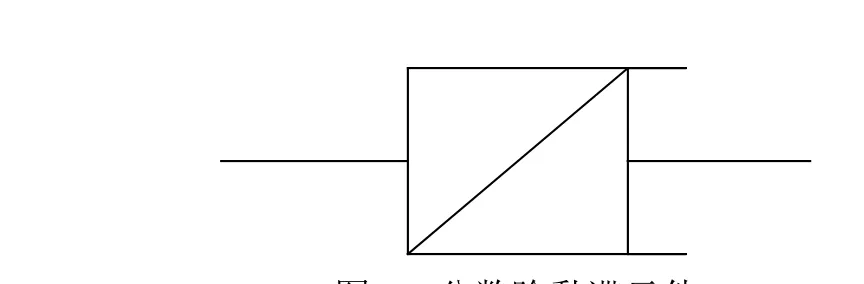
图6 分数阶黏滞元件Fig. 6 Fractional viscous element

3.2 非线性元件
由于Harris 函数是一种形式简单,曲线灵活的衰减型函数[21−22],有利于描述非线性衰减蠕变性质,因此采用该函数描述非线性衰减蠕变,其公式如下:

由式(7)建立非线性弹性元件,如图7 所示,其本构如下:
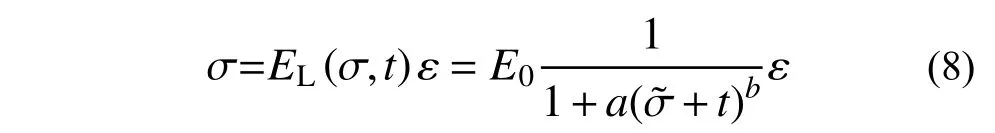

图7 非线性弹性元件Fig. 7 Nonlinear elastic element
2)非线性黏滞元件
由图5 可知:黏滞系数是应力的衰减函数,是时间的增函数。因此,提出 η的非线性公式如下:

图8 非线性黏滞元件Fig. 8 Nonlinear viscous element
3.3 非线性分数阶导数蠕变模型
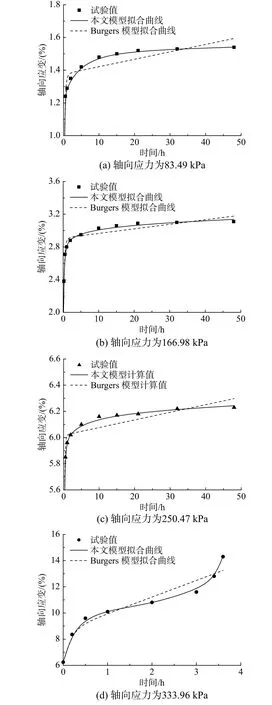
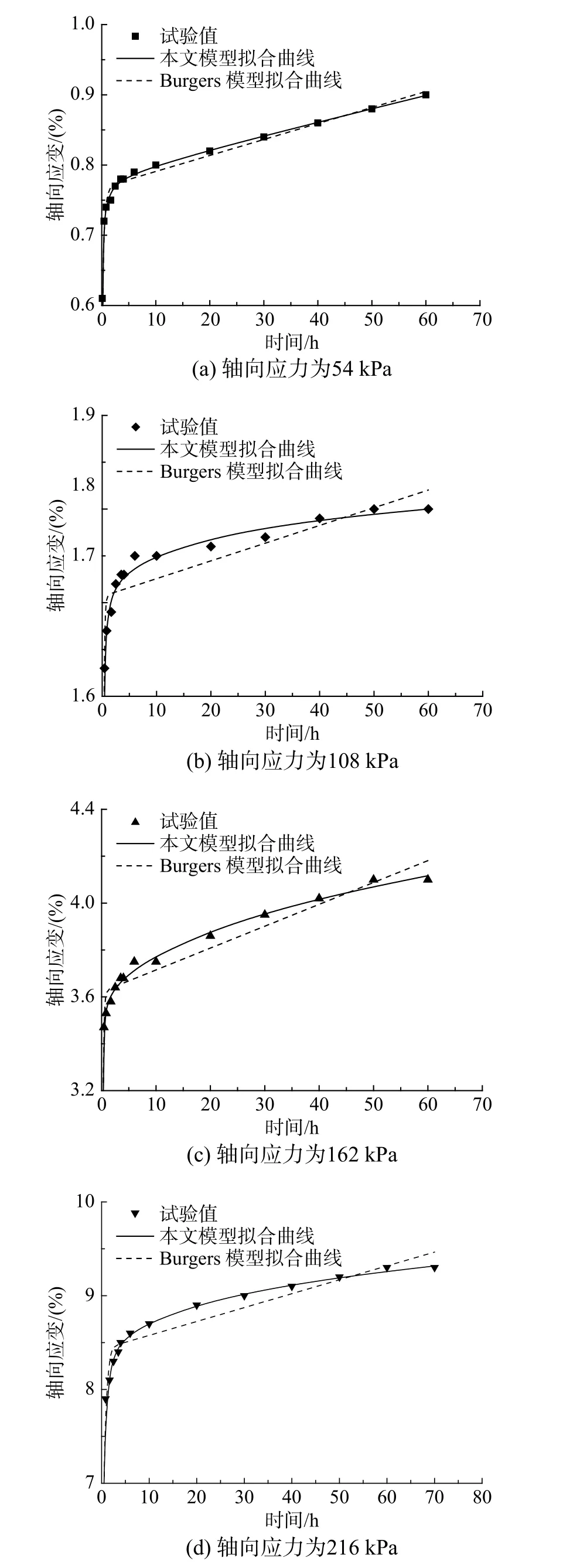
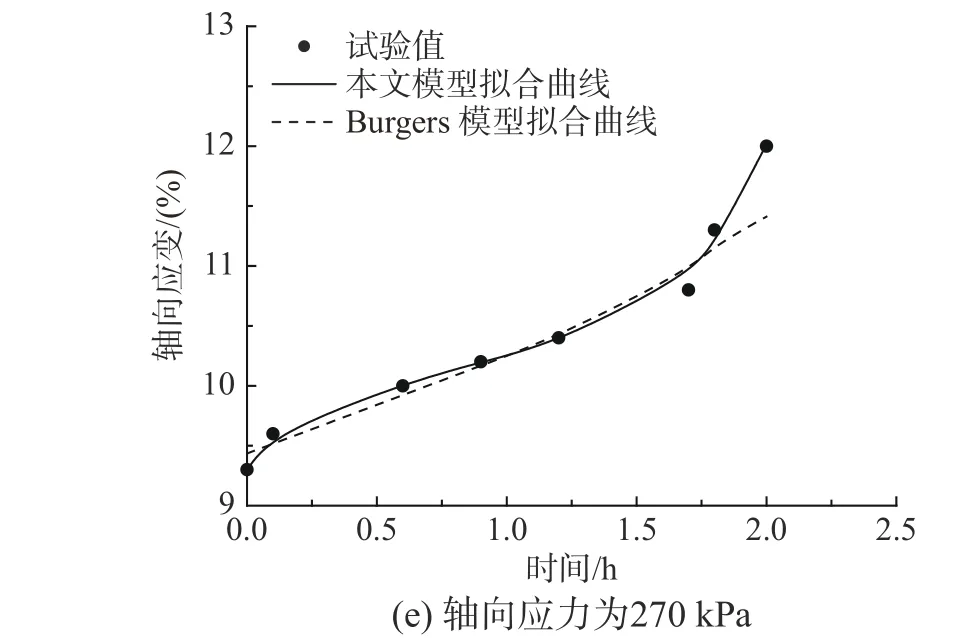
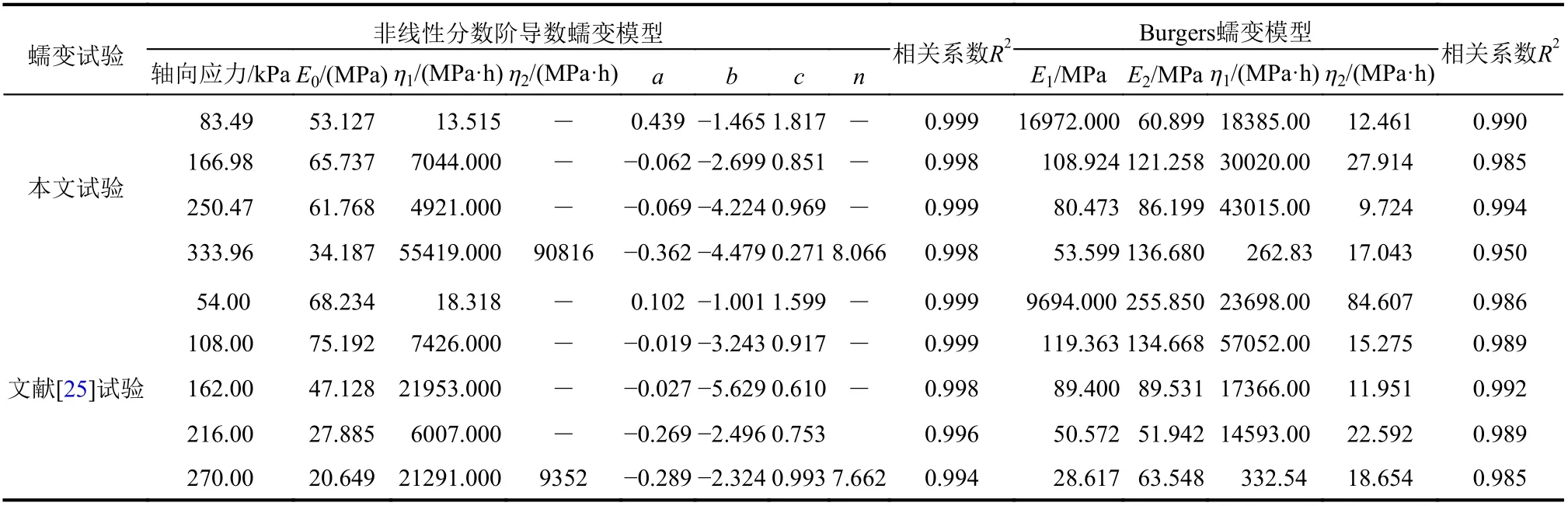
本文拟采用1 个非线性弹簧元件E、1 个非线性黏滞元件 η1、1 个分数阶黏滞元件 η2和1 个塑性元件V构建蠕变模型,如图9 所示。在图9 中,弹簧元件描述瞬时弹性变形;当 0 图9 非线性分数阶导数蠕变模型Fig. 9 Nonlinear fractional derivative creep model 当t=0 时,在模型上施加应力 σ,黏土变形有: 本文非线性分数阶导数蠕变模型与经典Burgers模型类似,后者具有能较好反映瞬时应变、初始蠕变和稳态蠕变、卸载后产生塑性变形等优点[24]。因此,分别利用本文蠕变数据和文献[25]中的蠕变数据对本文蠕变模型和经典Burgers 模型进行拟合分析。结果分别见图10、图11 及表2。 图10 本文蠕变试验拟合曲线Fig. 10 Fitting curves of creep test in this paper 由表2 可知,非线性分数阶导数蠕变模型在两个蠕变试验第一级加载时,拟合参数ab<0,c>1 表明EL(σ,t) 、 η(σ,t)均是时间和应力的增函数,可以理解为在加载较小应力时,土体力学性质整体增强;但随后ab>0 , 0 各参数的建议取值区间为:在低应力条件下,a的取值区间为(0.102, 0.439),b的取值区间为(−1.001, −1.465),c的取值区间为(1.599, 1.817);在中-高级应力条件下(第二级加载以后),a的取值区间为(−0.019, −0.362),b的取值区间为(−2.496,−5.629),c的取值区间为(0.271, 0.969);n的取值区间为(7.662, 8.066)。以上各参数取值区间仅为本文对成都黏土的建议取值区间。 由图10、图11 可知,在低应力阶段,两个蠕变模型与蠕变试验值的拟合度均较好,但随着应力和时间的发展,非线性分数阶导数模型与蠕变试验值的拟合度明显优于Burgers 模型,尤其是在加速蠕变阶段。综上所述,本文非线性蠕变模型是科学合理的,可更准确地反映黏土蠕变全过程。 图11 文献[25]蠕变试验的拟合曲线Fig. 11 Fitting curves of creep tests in Reference [25] 表2 两种蠕变模型的拟合参数Table 2 The fitting parameters of two creep models 针对黏土蠕变的非线性性质,以成都黏土为研究背景展开了蠕变试验;并根据试验结果、分数阶微积分理论及Harris 衰减函数,建立了非线性分数阶导数蠕变模型,主要结论如下: (1)根据成都黏土蠕变试验结果,发现成都黏土的变形主要包括瞬时弹性变形、衰减蠕变变形、稳态蠕变变形和加速蠕变变形;长期弹性模量随时间和应力的增加非线性软化,黏滞系数随应力的增加非线性软化,随时间的增加非线性硬化。 (2)基于分数阶微积分理论和Harris 函数,分别提出了分数阶导数黏滞元件、非线性弹性模量和非线性黏滞系数,并建立了模型简单、参数少和概念清晰的非线性分数阶导数蠕变模型。 (3)通过两组蠕变试验数据,对非线性分数阶导数蠕变模型及Burgers 蠕变模型进行拟合分析,发现前者各阶段的拟合系数均大于后者并大于0.99,各拟合参数的规律更明显,对黏土非线性蠕变规律的描述更为合理,综上所述本文建立的非线性蠕变模型是科学合理的,可更准确地反映黏土蠕变全过程。并给出了本文非线性蠕变模型各参数的建议取值区间。 应当指出,通过黏土蠕变试验,确定弹性模量和黏滞系数的非线性特性;在流变学理论和分数阶微积分理论的基础上,构建分数阶黏滞元件,非线性弹性模量和非线性黏滞系数,建立的非线性分数阶导数蠕变模型,是对黏土非线性蠕变规律研究的一种尝试和探讨,但是文中只通过两个蠕变试验对非线性分数阶蠕变模型进行辨识分析,所以蠕变模型的普适性还需要进一步验证。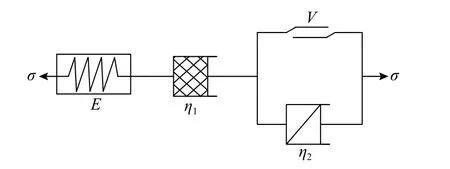

4 蠕变模型辨识及性质分析
4.1 蠕变模型辨识
5 结论
