基于积叠线的风扇叶片优化与振动特性研究
2020-09-16张效溥王仲林欧阳华
张效溥,王仲林,田 杰,2,3,陈 勇,2,3,欧阳华,2,3
(1.上海交通大学机械与动力工程学院,上海200240;2.燃气轮机与民用航空发动机教育部工程研究中心,上海200240;3.先进航空发动机协同创新中心,北京100191)
0 引言
航空发动机适航认证条例CCAR 33.83 规定:每型发动机必须进行振动测试,以确定可能受机械或空气动力导致激振的部件的振动特性在整个声明的飞行包线范围内是可接受的[1]。作为航空历史上销量最高的CFM56 系列发动机,虽然通过了适航认证且运行了上亿小时,但仍在2016 年[2]和2018 年[3]分别发生了2 次严重的发动机事故。初步报告指出事故原因是由于风扇叶片的高周疲劳导致在靠近叶片根部发生失效断裂,叶片飞出后造成非包容性损伤。可见风扇叶片的高周疲劳对发动机的安全性有很大影响。
国内外学者对航空发动机风扇叶片的振动特性和高周疲劳问题进行了大量研究。Cowles[4]总结了航空发动机高周疲劳产生的原因和研究方法;Ewins[5]归纳了旋转叶轮机械的振动来源,重点关注共振问题的避免和控制技术;Ni 等[6]通过仿真和试验方法研究了多模态激励下风扇叶片的应力特性;马艳红等[7]分析了离心力产生的弯矩和扭矩与气动力产生的弯矩复合作用对叶片静应力的影响,结果表明可以通过调节叶片积叠线的弯掠构型,使得附加弯矩与扭矩载荷相互抵消,降低叶片最大静应力;Deng 等[8]、Astrua 等[9]、张蓟欣等[10]以静应力和共振裕度为目标函数对叶片的积叠线进行优化,得到具有足够安全系数的叶片设计;Li 等[11]、Wang 等[12]、Samad 等[13-14]、Myoren 等[15]学者利用CFD 对叶片的积叠线弯掠造型进行优化,得到具有更好气动性能的叶片设计;Kou 等[16]和Simmons等[17]研究了气动载荷对叶片静频和动频的影响及共振下的应力分布,结果显示气动载荷对振动应力没有明显影响。上述基于叶片积叠线的优化研究主要考虑气动性能参数,将静应力和共振裕度作为限制条件,而对叶片振动应力及振动特性考虑较少。
本文通过航空发动机风扇叶片重心积叠线周向构型的优化设计,改善风扇的强度和振动特性。基于Kriging 代理模型和微种群遗传算法,建立了航空发动机风扇“参数化建模-有限元仿真-强度和振动特性优化”一体化平台。基于该平台对某宽弦风扇叶片进行优化设计,并对比分析原型风扇和优化后风扇的振动特性。
1 优化流程及建模
本文采用Kriging 代理模型和微种群遗传算法,通过Matlab 程序和批处理脚本,自动调用UG/NX 和ANSYS-APDL 等软件,实现了优化流程的自动化运行,建立了航空发动机风扇“参数化建模—有限元仿真—强度和振动特性优化”的一体化平台,如图1 所示。
从图中可见,首先利用均匀设计法构造设计变量矩阵,通过参数化建模、自动网格划分、有限元仿真及后处理得到完整的样本空间;其次建立代理模型,利用遗传算法搜索并预测使目标函数最小的设计变量组合;再次通过种群迭代直到目标函数达到收敛准则;最终将满足设计要求的最优解生成叶型,优化过程结束。
1.1 基于Kriging 模型的优化算法
在计算资源有限的情况下,代理模型使用少量的数据点即可对整个样本空间进行较高精度的预测[13]。本文采用Kriging 插值模型为代理模型,将微种群遗传算法作为优化算法对风扇叶形进行优化设计,大大降低了优化所需要的计算资源和时间成本。
1.1.1 Kriging 模型的构建
Kriging 模型通过将样本函数线性加权,得到响应值与设计量之间的近似插值函数,对最优设计变量进行预测,插值函数的基本形式为

式中:f(x)为未知的全局近似值;Z(x)为均方差为σ、均值为0 的高斯随机函数。
空间内不同变量之间的相关性由协方差矩阵函数表示为

式中:R 为对角线对称的相关矩阵;C 为矩阵中的相关函数;θ 为待训练参数。本文相关系数选取各向同性的高斯指数模型,取光滑因子p=2,其表达式为

根据插值函数无偏性的特点,推导出未知点处预估函数值为
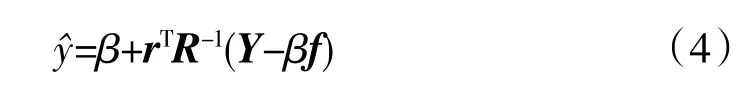
式中:r 为空间内未知点与样本点之间的相关向量,β 及β 的标准差为
1.1.2 Kriging 模型训练
Kriging 插值模型优劣的关键在于参数的选取,本文采取最大似然估计法作为训练的依据,最终将问题转化为使下式最大

由于无法直接求解θ,因此需要采用合适的优化算法。比较常见的算法为模式搜索算法,但是该算法对初始设计变量的依赖性很高[18],会影响Kriging 模型的训练结果。本文采用微种群遗传算法,相比传统的遗传算法,微种群遗传算法的种群较小,遗传操作采取锦标赛选择和均匀交叉算子,并且略去了变异操作,因此拥有更高的收敛速度和全局寻优能力[19-20]。
1.1.3 最优解的求取
本文采取EI 函数来求得最优解,其定义为
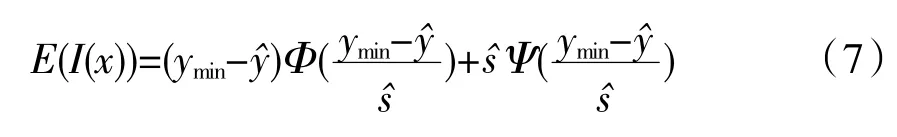
式中:Φ 和Ψ 分别为标准正态分布的分布函数和密度函数;和分别为x 处的代理模型估计值及标准差;ymin为当前样本库中的最优函数值。
EI 函数可以有效地表征目标函数的改善量,因此在约束范围内求解出使EI 函数达到最大值的x 即为预测最优解。与代理模型的训练相似,本文采用微种群遗传算法求解x,有效克服了传统惩罚函数法中收敛性较差、惩罚因子难以选取的问题[21],大幅度减小了计算量。
1.2 风扇叶片参数化建模
为了在优化过程中实现自动建模和划分网格,需要将叶片模型参数化处理。首先将叶片以流道线为界分成叶型和叶根2 部分,仅对叶型部分进行优化。为了提取原型叶片的截面和积叠线,以风扇旋转中心为轴,利用圆柱面和圆锥面分别截取叶型,得到16 组叶型截面,通过积分法求得重心积叠线的坐标。其次,选取第7、11 和15 截面的重心作为控制点[10,22],如图2所示。这样既保证叶型与伸根段的光顺连接,又避免对叶尖造型造成较大影响。优化过程中改变控制点的坐标,通过样条插值得到新的积叠线,通过曲面网格法生成新叶型。最后,将新叶型与叶根进行光滑性拼接后得到新叶片模型。在ANSYS-APDL 中通过扫掠生成结构化网格,包括18976 个单元和25602 个节点,得到网格质量良好的有限元模型,如图3 所示。在有限元计算中,对榫头上表面节点施加法向约束,对榫头前端面施加轴向约束。
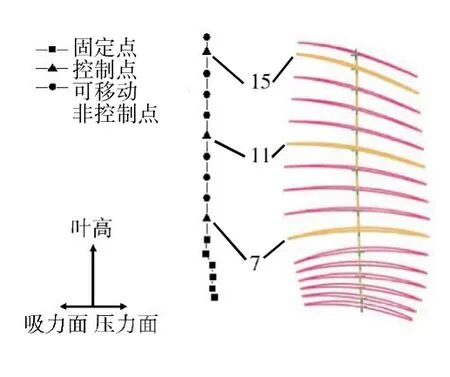
图2 叶片型线的提取和积叠线的生成

图3 叶片有限元模型及网格划分
1.3 设计参数与目标参数
1.3.1 设计参数
文献[7]中的结果表明:叶片积叠线的弯掠构型使得附加弯矩与扭矩载荷相互抵消,从而降低叶片最大静应力。虽然风扇叶片的气动载荷和静态变形存在耦合关系,但相比于叶片的掠型,弯型的小偏移量对气动参数影响较小,气动参数的微小变化也不会对叶片的振动应力产生明显影响。文献[23]对比了单独离心载荷与离心和气动载荷同时作用下风扇叶片的固有频率、共振裕度及振动应力,结果显示:气动载荷对叶片的振动应力等特性影响较小。为此本文仅对叶片的周向积叠线进行小范围优化,且不考虑气动载荷的影响。
在叶片参数化建模中截取16 个截面,如果将所有截面的周向坐标作为设计参数,很可能导致叶片表面呈现波纹状不光顺的造型。因此设计参数选取积叠线上3 个截面重心作为控制点,每个截面的周向坐标作为设计参数,通过3 次样条生成新的积叠线。为了保证与叶根的光顺连接且叶尖位置造型上与原始叶片没有太大的区别,靠近叶根的1~5 号截面重心设为固定点,16 号截面和15 号截面保持相同的位移。这样的设计参数可保证尽可能减小对气动性能的影响。
1.3.2 目标参数
大涵道比涡扇发动机风扇叶片由于尺寸较大且转速较高,在工作中会产生很大的离心应力,这对叶片的结构强度提出很高要求。现有涉及叶片重心积叠线优化的文献中均将最大静应力作为约束条件或目标参数,但由于风扇叶片在工作中受到来自发动机进口的多种激励,如流场畸变、地面吸涡等,还受到流道内涡流和湍流的激励。这些来自气动载荷的激励通常具有一定的频率特征,使风扇叶片产生剧烈的振动甚至是颤振,对风扇的安全性和可靠性有很大影响。因此,为了使优化后叶片的振动特性满足要求,除最大静应力Smax之外,还引入模态振动应变能密度指数作为优化目标。
应变能密度可表征应变状态。应变能密度准则常被用来判断弹塑性材料的失效断裂及裂纹扩展[24-26]。本文选择的是应变能密度指数κ,其定义为叶片表面最大应变能密度ρmax,SEDe与平均应变能密度的比值

式中:上标m 表示第m 阶模态。
应变能密度定义为
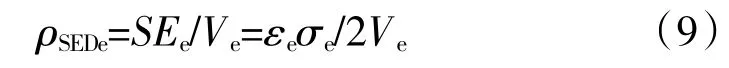
式中:εe、σe和Ve分别为单元的应变、应力和体积。
指数κmax的相对值表征了不同叶片设计的应变能密度的集中程度。叶片的κmax值越小,其应变能分布越均匀,最大应变值相对较低,叶片的疲劳寿命更长。由于优化过程中的种群最优解是通过目标参数值对比得到的,所以应变能密度指数适用于优化过程中表征叶片的振动特性。
在发动机工作中,风扇叶片的第1 阶弯曲模态会受到侧风、进气畸变、吸涡等激励,而且颤振也经常发生在第1 阶模态。第1 阶模态的振幅和能量都明显高于其他阶次,所以在工程中更关注第1 阶模态的振动。本文在优化中将第1 阶模态的应变能密度指数κ1max作为代表振动特性的目标参数。考虑到静应力和应变能密度指数的数量级和量纲不同,分别通过原始模型的参数值对目标参数进行归一化处理,再加权得到最终的目标参数f,本文选取权重系数c1=c2=1。
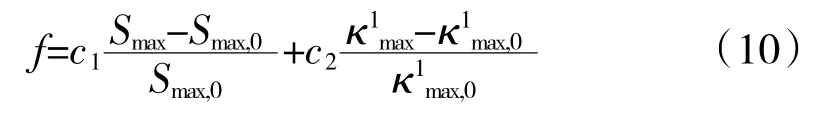
2 优化设计算例
基于上述优化流程,将某宽弦风扇叶片作为优化对象,进行周向积叠线优化,其设计及材料参数见表1。在有限元静力分析中施加转速载荷,模态分析和谐响应分析分别采用Block Lanczos 法和完全法,均考虑了离心力产生的预应力。

表1 原型叶片的材料及设计参数
7、11 和15 号截面重心的周向偏移量分别记为x1、x2和x3。文献[27]表明:叶片弯向构型会促使附面层低能流体向叶中移动,对喘振裕度、气动噪声等产生一定影响。因此,为了保证叶型的光滑性并使其气动性能影响尽可能小,设置其变化范围分别为-2~2 mm、-3.5~3.5 mm 和-5~5 mm。则该优化问题可表示为

使用代理模型优化算法,先分别以静应力(参数A)和应变能密度指数(参数B)为单目标函数进行优化,再对二者加权的复合目标函数(C)进行优化。经过50 次迭代后,优化结束。原型与C 参数优化后的叶型积叠线对比如图4 所示。从图中可见,3 个控制点都向吸力面偏移,中间的控制点偏移比两端的大,叶片整体呈“C”型。样本库内最优值随着迭代次数变化如图5 所示。
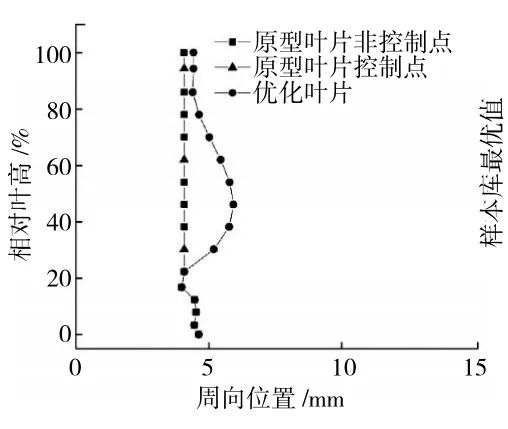
图4 优化前、后的重心积叠线

图5 样本库最优值与迭代次数的变化
优化后的设计参数见表2。从表中可见,单目标参数优化的结果在改善了目标参数的同时,导致另一参数的恶化,而双目标参数加权的优化结果使得2 个参数都得到了改善。最大静应力相比原型叶片减小了5.45%,第1 阶应变能密度指数减小了5.94%。
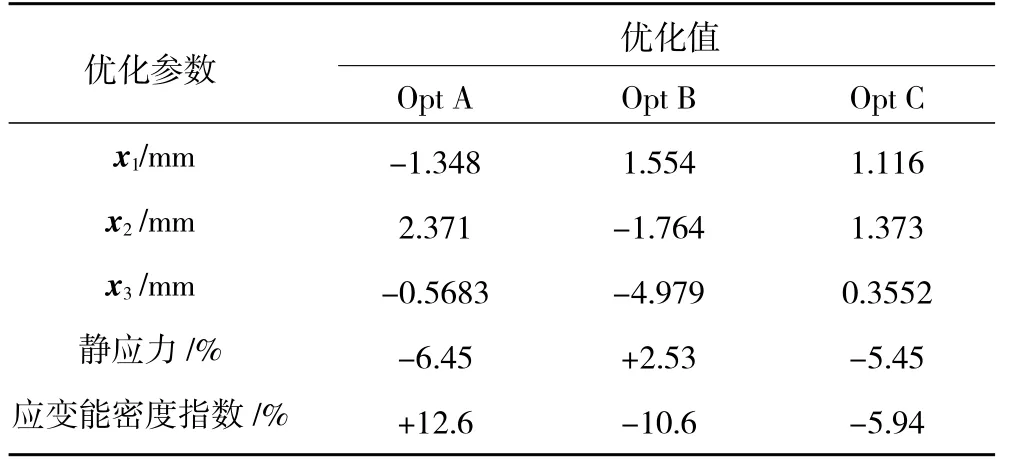
表2 优化叶片与原型叶片参数对比
优化前、后的等效静应力如图6 所示。从图中可见,原型叶片的2 个高应力区域分别位于叶根前缘和叶型中部。静应力的最大值位于吸力面的叶根前缘,叶片中部的静应力具有宽弦风扇叶片典型的“靶心”式分布。相比之下,优化叶片的最大应力也出现在叶根前缘,但是数值减小了5.45%,叶片安全系数则由1.29 提高到1.37。同时,叶片中部的高应力区向叶尖方向移动;叶根前缘处较高应力区的应力水平也得到了较明显的改善。
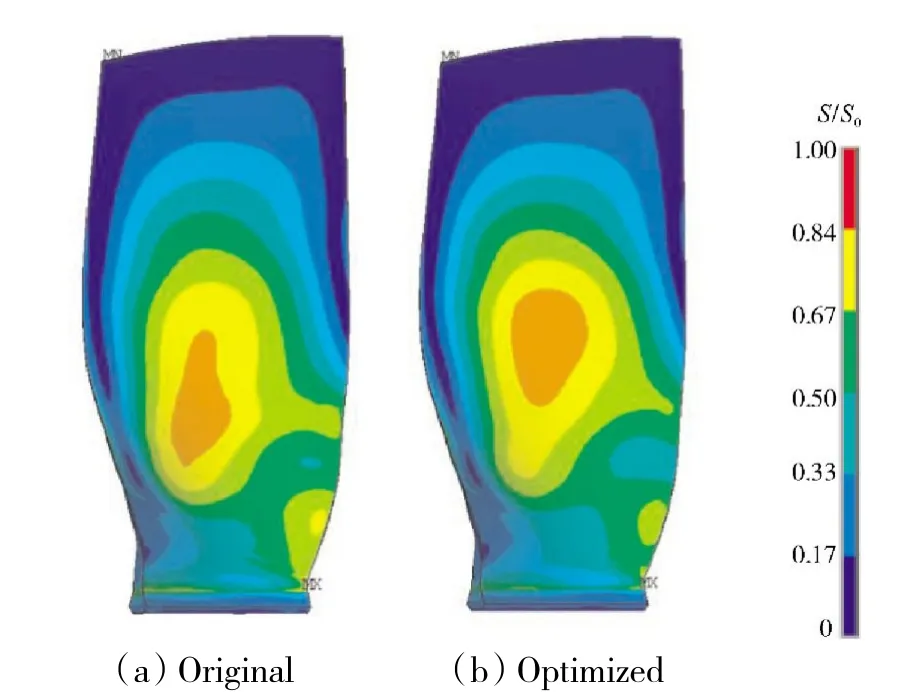
图6 优化前、后叶片Von Mises 静应力
优化前、后的第1 阶模态应变能密度分布如图7所示。从图中可见,原形在叶片中心有1 个较高幅值区域。而在优化叶型中,该区域幅值有所减小。同时,原型叶片的应变能密度集中于前缘,而优化叶片高应变能密度区域分成了2 个应变能密度相对较低的区域,最大值点位置没有明显变化,且峰值降低了5.94%。说明叶片的应变能密度分布得到了改善。
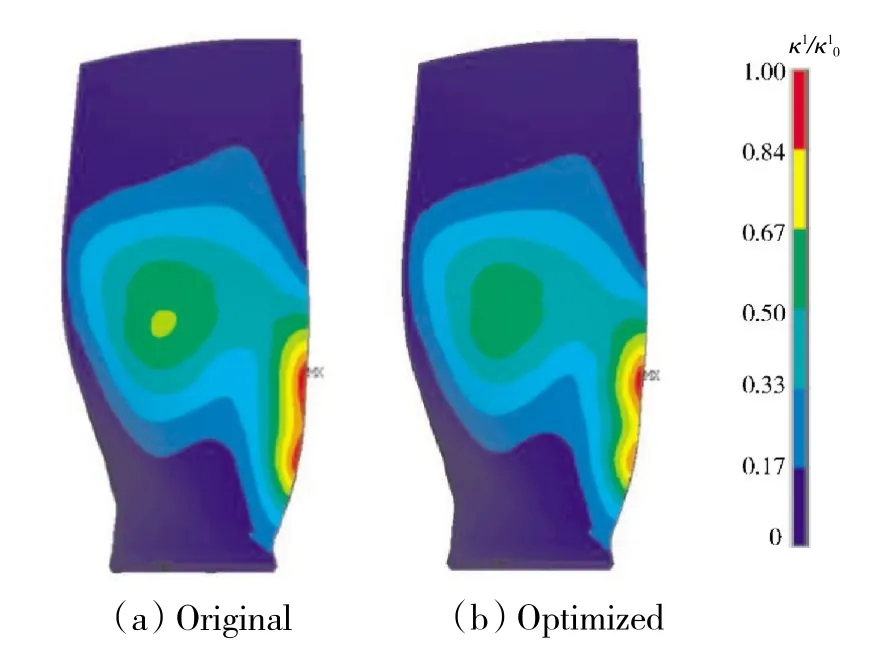
图7 优化前、后1 阶应变能密度指数
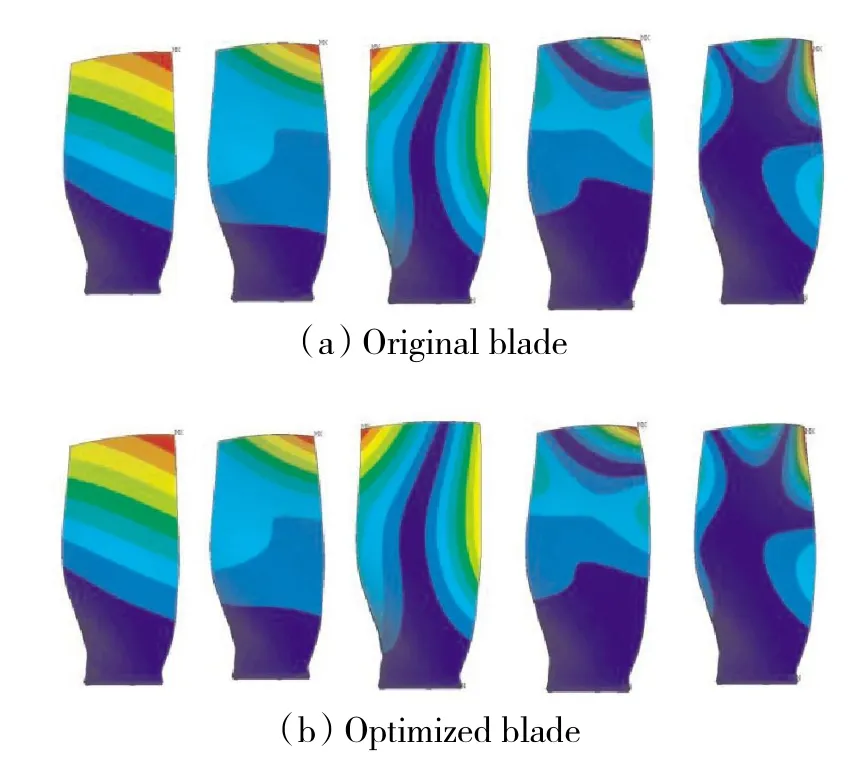
图8 优化前、后前5 阶振型
除了作为目标参数的静应力和应变能指数以外,风扇叶片的固有频率及振型、共振裕度和weaklink 也是衡量振动特性的重要指标。叶片前5 阶振型如图8所示。图中从左至右依次为第1 阶周向弯曲模态、第1 阶轴向弯曲模态、第1 阶扭转模态、第2 阶弯曲模态及第2 阶弯扭组合模态。结果显示优化前、后的前4 阶振型基本不变,第5 阶振型在后缘处有一定的差别,可见高阶复杂振型对积叠线的变化更敏感。
原形叶片和优化后叶片在不同转速下的固有频率如图9 所示。从图中可见,二者在前6 阶的固有频率基本一致。由坎贝尔图可以得到叶片在各转速下的共振裕度。对于工程上较关注的第1 阶模态,从转速为60%~105%内,优化前、后叶片的共振裕度都保持在20%以上,相互差别极小,对比见表3。因此优化设计没有对共振裕度产生明显影响。
振动应力裕度基于Goodman 曲线,在考虑静应力的基础上可评估振动应力到许用应力的裕量,是评价叶片高周疲劳特性的重要指标。Goodman 曲线如图10 所示,直线上方的区域代表高周疲劳的危险区域。考虑叶片材料属性和加工的不确定度,需要在设计中留有足够应力裕度。振动应力裕度M 定义为考虑静应力下,实际振动应力σv与许用振动应力σA的相对差值

图9 优化前、后叶片的故有频率

表3 优化前、后转速为60%~110%时第1 阶频率裕度

为了对比优化前、后的应力裕度,在谐响应分析中对叶片施加周期性全局加速度载荷,载荷频率为叶片的第1 阶固有频率,计算得到振动应力从而求得第1 阶模态的应力裕度。结果显示优化后的第1 阶振动应力裕度从66.81%提高到70.46%。
在应力裕度的基础上,对叶片高周疲劳的失效位置,即weaklink 进行评估。通过仿真计算得到每个节点的静态应力和模态应力,再通过对模态应力的等比例缩放,使得刚好有1 个节点在Goodman 曲线上。这1 点就代表了某个固有模态阶次振动下最先发生高周疲劳失效的位置,即weaklink 点。优化前、后叶片的第1 阶weaklink 结果如图11 所示。从图中可见,原型叶片有3 个节点(A、B 和C)同时接近Goodman 曲线,均位于前缘根部。优化后叶片的weaklink 点仍然为这3 个点。由于优化叶片静应力水平较低,3 个点在坐标图上明显向左偏移,且对应的第1 阶振动应力裕度均有所增大,说明叶片的高周疲劳特性得到了改善。
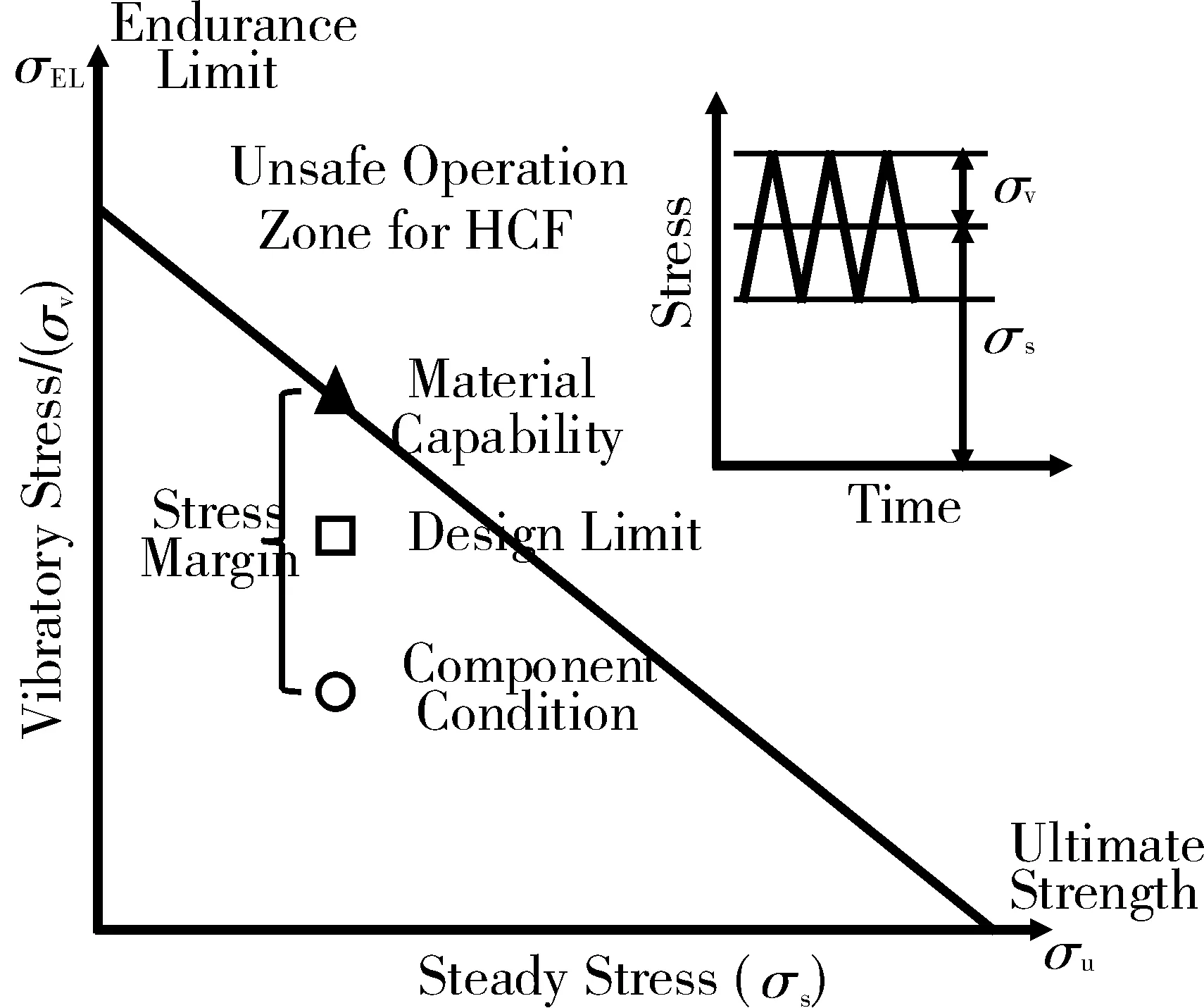
图10 修正的Goodman 曲线[4,28]
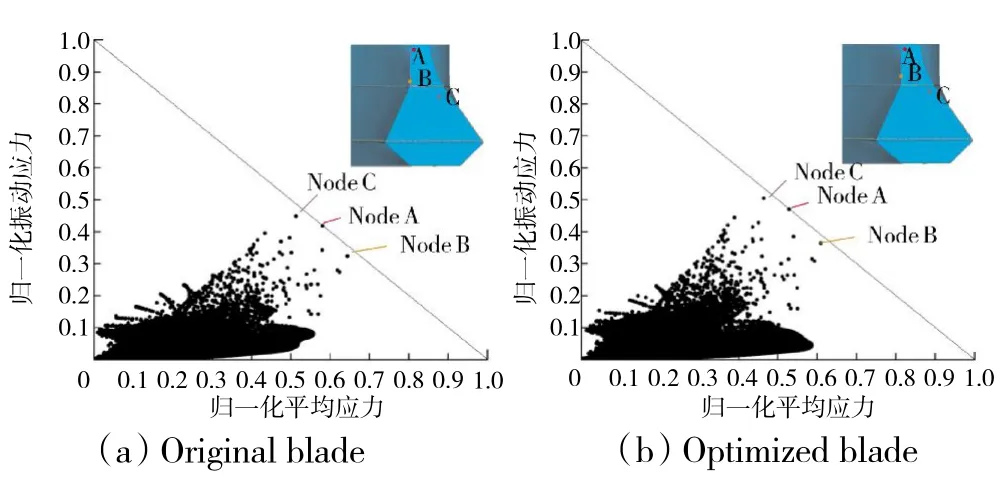
图11 优化前、后叶片的Weaklink
3 结论
本文对风扇叶片重心积叠线弯曲构型进行了参数化建模,使用Kriging 代理模型和微种群遗传算法搭建了风扇叶片强度和振动特性的一体化平台,对某宽弦风扇叶片的积叠线进行优化设计,得到了如下结论:
(1)基于重心积叠线周向构型对风扇叶片进行参数化建模和自动化网格划分。结合Kriging 代理模型和微种群遗传算法,综合考虑静应力和应变能密度指数为优化目标函数,建立了航空发动机风扇“参数化建模—有限元仿真—强度和振动特性优化”一体化平台。
(2)基于该平台对某型宽弦风扇叶片改型后的直叶片进行了优化,得到优化设计的各项目标参数均有改善。优化后的叶片静应力在叶片中心高应力区向叶尖偏移,叶根前缘的应力集中得到改善,且最大静应力比原型叶片的减小了5.45%,第1 阶应变能密度指数减小了5.94%,相比于单目标优化结果更加全面有效。
(3)对比优化前、后叶片的振动特性发现,叶片的振型、固有频率和weaklink 点没有明显变化,第1 阶振动应力裕度从66.81%提高到了70.46%。说明优化流程有效地改善了叶片的强度和高周疲劳特性,且对其他振动特性没有负面影响。
