1 种航空发动机整机质量分配方法
2020-09-16郑伟连杨纯辉刘仕运
郑伟连,杨纯辉,刘仕运
(1.中国航发沈阳发动机研究所,沈阳110015;2.空军装备部驻沈阳地区第二军事代表室,沈阳110043)
0 引言
推重比是衡量战斗机发动机技术水平和作战效能的重要指标之一。为了实现航空发动机的推重比指标,在设计过程中对整机质量有严格的要求。在发动机方案设计阶段,将发动机整机质量指标合理地分配给各设计单元是实现整机质量控制的重要手段。
相关学者对涡喷、涡扇发动机质量的估算方法开展了大量研究。王团结等[1]建立了采用粒子群优化算法的BP 神经网络发动机质量估算模型;张韬等[2]根据发动机部件法的思想,建立了基于统计的各部件气动-结构经验关系模型,发展了变循环发动机质量预估方法;潘代锋等[3]从发动机热力循环参数出发,通过流路分析确定总体轮廓尺寸,进一步获得主要零件的几何尺寸并估算发动机质量。但是,鲜有关于航空发动机整机质量分配技术方面的研究。
本文对发动机整机质量目标进行了定义,提出了1 种在方案论证阶段将发动机整机质量名义值和质量公差向各设计单元分配的方法。
1 整机质量目标定义
在发动机方案论证阶段,航空发动机的质量目标来源为:
(1)对于1 台新研制的发动机,通过整机质量估算方法得到发动机的整机质量名义值m0;
(2)承接发动机用户的质量指标要求,一般为发动机整机质量的最大值mmax。例如:某型航空发动机用户要求的发动机干质量指标为不大于1780+2%kg,即整机质量不超过1815.6 kg。
以上质量指标仅明确了发动机整机质量的名义值或质量最大值,以此作为发动机整机质量目标,不能够准确地表征和描述发动机整机质量值的随机性。同时,以上的质量指标未对发动机整机的质量公差进行定义,无法满足发动机整机质量的分配需求。
考虑到航空发动机制造过程中存在的系统误差和随机误差,假设发动机整机质量分布服从正态分布,如图1 所示。定义发动机整机质量目标为(μ,σ),其中μ 为发动机整机质量名义值,σ 为整机质量公差值。发动机整机质量公差范围为(μ-σ,μ+σ)。
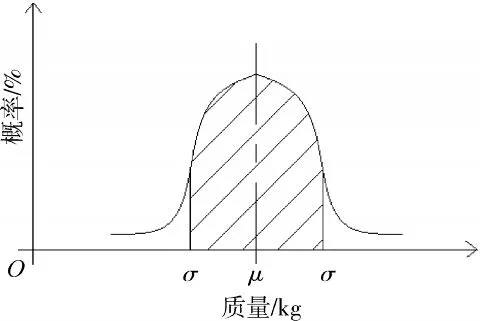
图1 发动机整机质量目标
2 整机质量分配流程
航空发动机采用单元体思想开展设计工作,单元体是航空发动机的设计、装配单元。在发动机方案设计阶段,发动机总体设计专业人员需要将整机质量的名义值和公差分配给各单元体,某型双转子涡轮风扇发动机的单元体划分为进气机匣、风扇、中介机匣、中央传动机匣及第2 和第3 号轴承、高压压气机转子、高压压气机前机匣、高压压气机后机匣、燃烧室机匣、燃烧室火焰筒、高压涡轮导向器、高压涡轮转子、高压涡轮机匣、低压涡轮、涡轮后机匣、混合器、加力扩散器、收-扩喷管、附件机匣、外涵机匣。
整机质量名义值分配和整机质量公差值分配的流程如图2 所示。
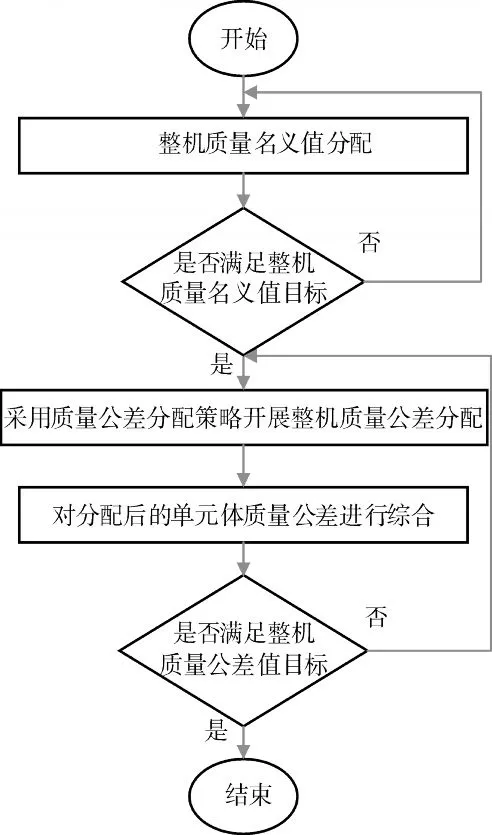
图2 发动机整机质量分配流程
从图中可见,整机质量分配后,确认整机质量名义值和公差值是否满足整机质量目标。如果满足质量目标,则结束质量分配工作;如果不满足整机质量目标,则调整单元体的质量分配结果,将整机质量重新分配,直至满足整机质量目标要求。
3 整机质量名义值分配
发动机整机质量名义值向各单元体分配的策略可表示为

式中:n为发动机单元体总数;μi为第i 个单元体的质量名义值。
对于从原型机改进研制的改型发动机,其各单元体质量名义值可以参考已有原型机对应的单元体质量。针对改型机相对于原型机中单元体结构的改进设计,在整机质量名义值分配过程中,以原型机单元体质量为基础进行修正得到改型机单元体质量名义值。
例如:某推力级别的叶型改进结构的3 级风扇单元体的质量名义值为

式中:M1为改进叶型结构的风扇单元体质量名义值;M0为某推力级别的3 级风扇的名义质量;α 为修正系数,具体值依据改进结构的具体情况确定。
对于没有原型机的全新研制的发动机,首先利用质量估算经验公式或软件对发动机各单元体的质量进行估算,然后以估算的结果为依据确定单元体质量名义值,最终实现发动机整机质量名义值的分配。
4 整机质量公差的分配
发动机整机质量公差向各单元体分配的策略可表示为

式中:σi为第i 个单元体的质量公差值。
发动机整机质量公差分配受多种因素影响。单元体加工成本、其质量在整机质量的占比、零组件特性都会影响单元体质量公差的确定。
4.1 单元体加工成本的影响
工程实践表明,零组件的质量公差和加工成本为负相关的关系,即质量公差越小,生产加工成本越高。在质量公差的分配过程中,如果某单元体的质量公差分配较大,其加工成本相应会降低;反之,如果分配的质量公差较小,则其加工成本会增加。定义单元体加工成本因素对质量公差分配的影响因子为k1。
4.2 单元体质量占比的影响
每台发动机单元体的质量在发动机整机质量中所占的比例不一样。在发动机整机质量公差分配时,需要考虑各单元体质量在整机质量的占比来确定单元体质量公差值。例如:某单元体质量占整机质量的比例较大,该单元体的质量公差分配就需要重点考虑;相反,对于发动机中质量占比较小的单元体,其质量公差分配可以相对大一些。定义单元体质量占比因素对质量公差分配的影响因子为k2。
质量占比的影响因素可表示为
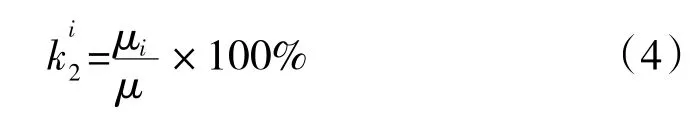
4.3 单元体零件特性因素的影响
航空发动机零件按功能分为支撑结构件、转子件、联结件等;按应用特性又分为普通件、关键件、重要件等。发动机中的某些转子件,如盘轴、叶片等,由于其结构的重要性,设计精度要求比较高,多数都采用机加、精密铸造等方式制造,因此一般要求其具有较小的质量公差值;另外,一些采用铸造方式生产的支撑结构类的零件,由于其工作环境要求不高,其设计精度要求也比较低,因此其质量公差相对较大。定义单元体零组件特性因素对质量公差分配的影响因子为k3。
单元体的零件特性因素影响因子可以采用权重系数法确定。定义单元体或组件中关键件的数量为a,其总质量为ma;重要件的数量为b,其总质量为mb;一般件的数量为c,其总质量为mc;暂不考虑螺帽、螺钉、锁片等小零件。定义关键件的权重系数为ηa,重要件的权重系数为ηb,一般件的权重系数为ηc,则组件的考虑零组件特性的综合权重系数η 为

ηa、ηb、ηc的具体数值由专家系统打分评定。考虑上述影响因素,实现质量公差分配
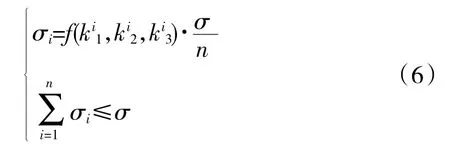
5 加工成本-单元体质量公差模型
加工成本是影响单元体质量公差的重要方面。在发动机制造过程中,零组件的质量公差与加工成本相关。采用不同的加工方法,零组件的质量公差不同,产生的加工成本也不同。总体来说,加工成本和质量公差成反比关系。
不同的零组件质量公差需要采用不同的加工工艺和制造资源来实现。制造资源主要包括制造装备、工艺装备、工艺技术和人力资源。具体影响到加工成本的因素有7 类[4-5]:设备价值、工艺方法、工序次数、工序工时、刀具和工具价值、检测工具价值、操作工人技术等级。这些因素都会对产品成本产生不同程度的影响,影响是综合、复杂且常常是模糊的,可以把各种因素按照一定的规则分为若干等级,并采用模糊数学理论对各加工因素进行处理:
首先应用二元对比排序法确定各类加工因素对成本影响的权系数,即先在二元对比中建立比较级;然后再按一定方法转化为总体的排序;最后对结果进行归一化处理,确定出各类加工因素对成本影响的权系数
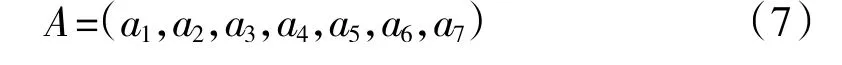
式中:a1~a7分别为7 种加工因素对成本影响的权系数。
每类加工因素按照一定的规则(如按等比、等差)分成若干等级,专业人员对各等级评判给分并采用数理统计处理的方法确定各等级对加工成本的影响系数。
零组件的几何形状、尺寸千差万别,很难用1 个数学模型精确描述所有尺寸的“加工成本-质量公差”,因此国内外还未建立成熟的发动机零组件加工成本和质量公差的数学模型。
本文采用基于模糊神经网络建立的“加工成本-质量公差”模型,为单元体质量公差的分配提供依据。把加工成本看成是质量公差值T 和加工因素成本影响系数V 的函数,并利用神经网络的高度非线性映射的特点,同时考虑到加工因素影响系数的模糊性问题,建立基于模糊神经网络[6-8]的“加工成本-质量公差”模型。该网络的输入为零组件的质量公差值T 和加工因素成本影响系数V,输出为加工成本。
模糊神经网络选用具有实数输入的模糊神经元,这种模糊神经元有N个非模糊输入,加权操作由隶属度函数代替[9]。把质量公差和加工因素成本影响系数作为模糊神经网络的输入,神经元结构如图3 所示。
加权操作由隶属度函数代替,⊗表示累积算子,则模糊神经元的数学表达式为
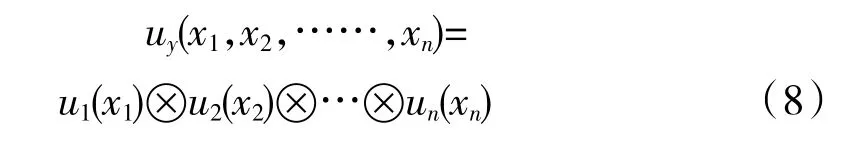
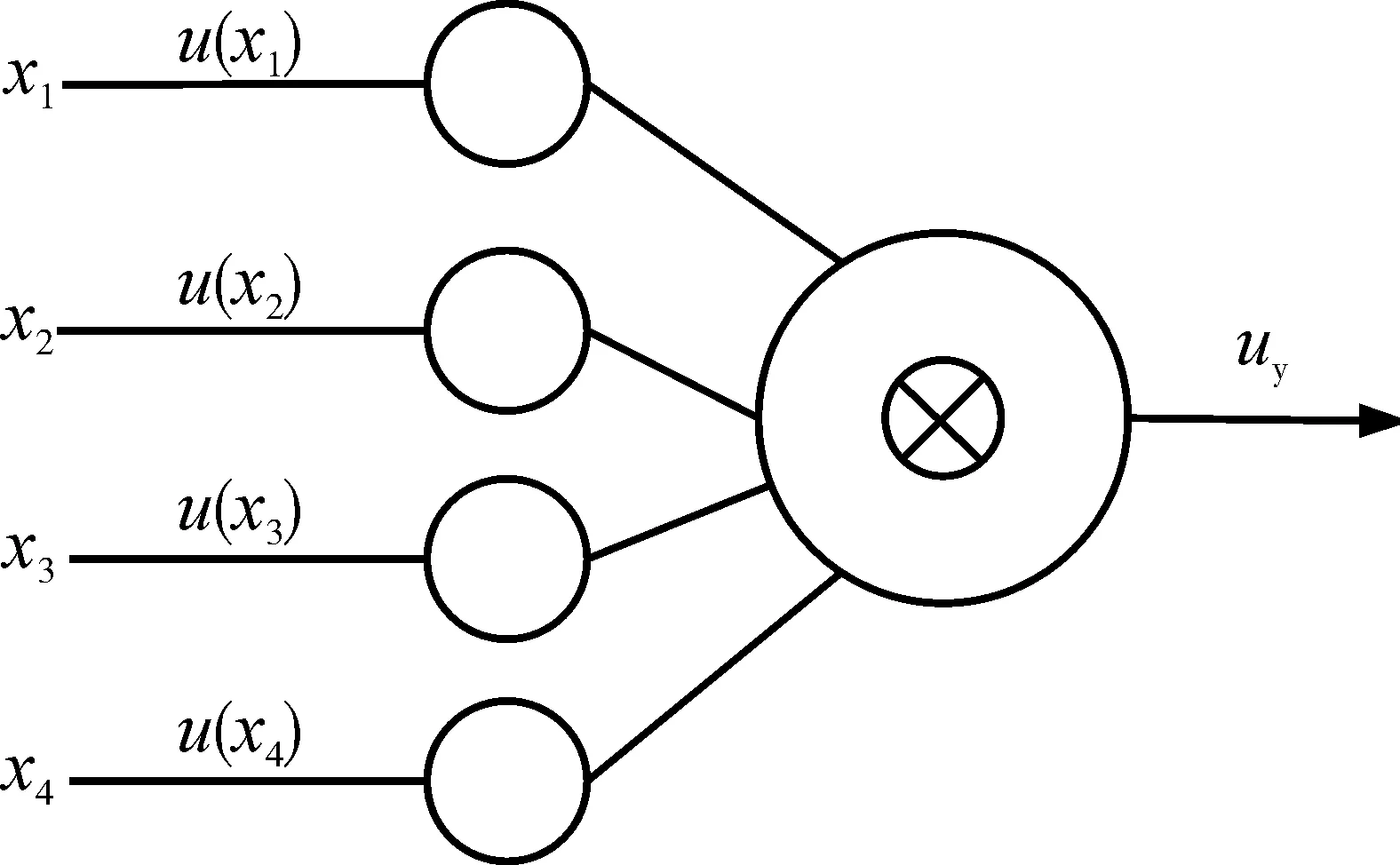
图3 神经元结构
式中:x1,x2,…,xn为单元体质量公差;u1,u2,…,un为质量公差的加工因素成本影响系数;uy为加工成本。
“加工成本-单元体质量公差”模糊神经网络模型4 层结构如图4 所示。
从图中可见,第1 层为输入层。
第2 层的作用是计算各输入分量的隶属度。采用高斯函数作为隶属度函数
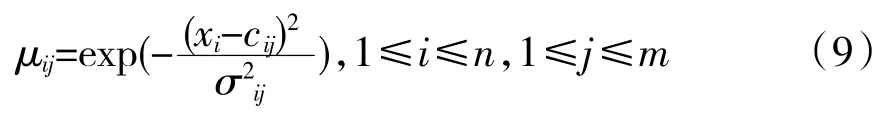
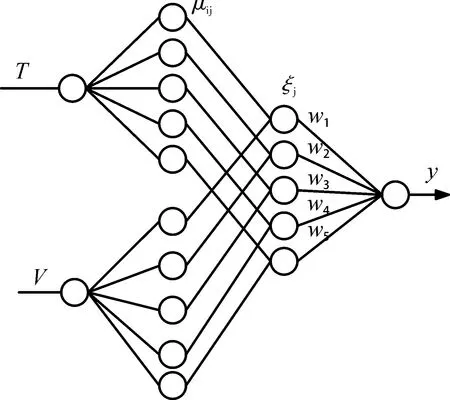
图4 “加工成本-单元体质量公差”模糊神经网络模型
式中:xi为第i 个输入;n 为输入层结点数;μij、cij、σij分别为隶属度函数、隶属度函数的中心及宽度;下标i表示第i 个输入,j 表示推理结点的序号。
第3 层为推理层,每个节点对应于1 条模糊规则
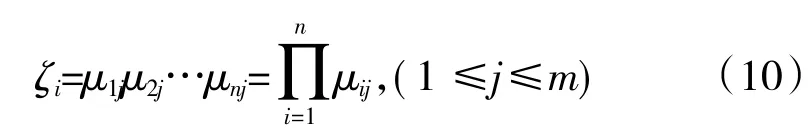
第4 层为反模糊化层。将第3 层的结果通过一定的权值组合出最后的输出结果
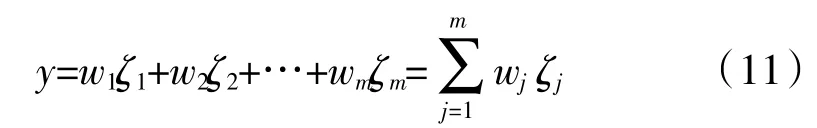
式中:wj为连接权值。
模糊神经网络的学习算法采用梯度下降法,在学习过程中对cij、σij、wj的调整量Δcij、Δσij、Δwj可表示为
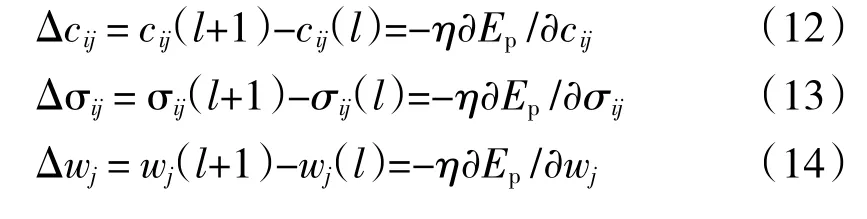
式中:η 为权值学习系数;Ep为网络目标函数;l 为迭代步数。
模糊神经网络选用的目标函数[10-11]为

式中:yd为网络期望输出;yc为网络实际输出;Ep为期望输出和实际输出的误差。
网络算法的具体计算流程如图5 所示[12]。
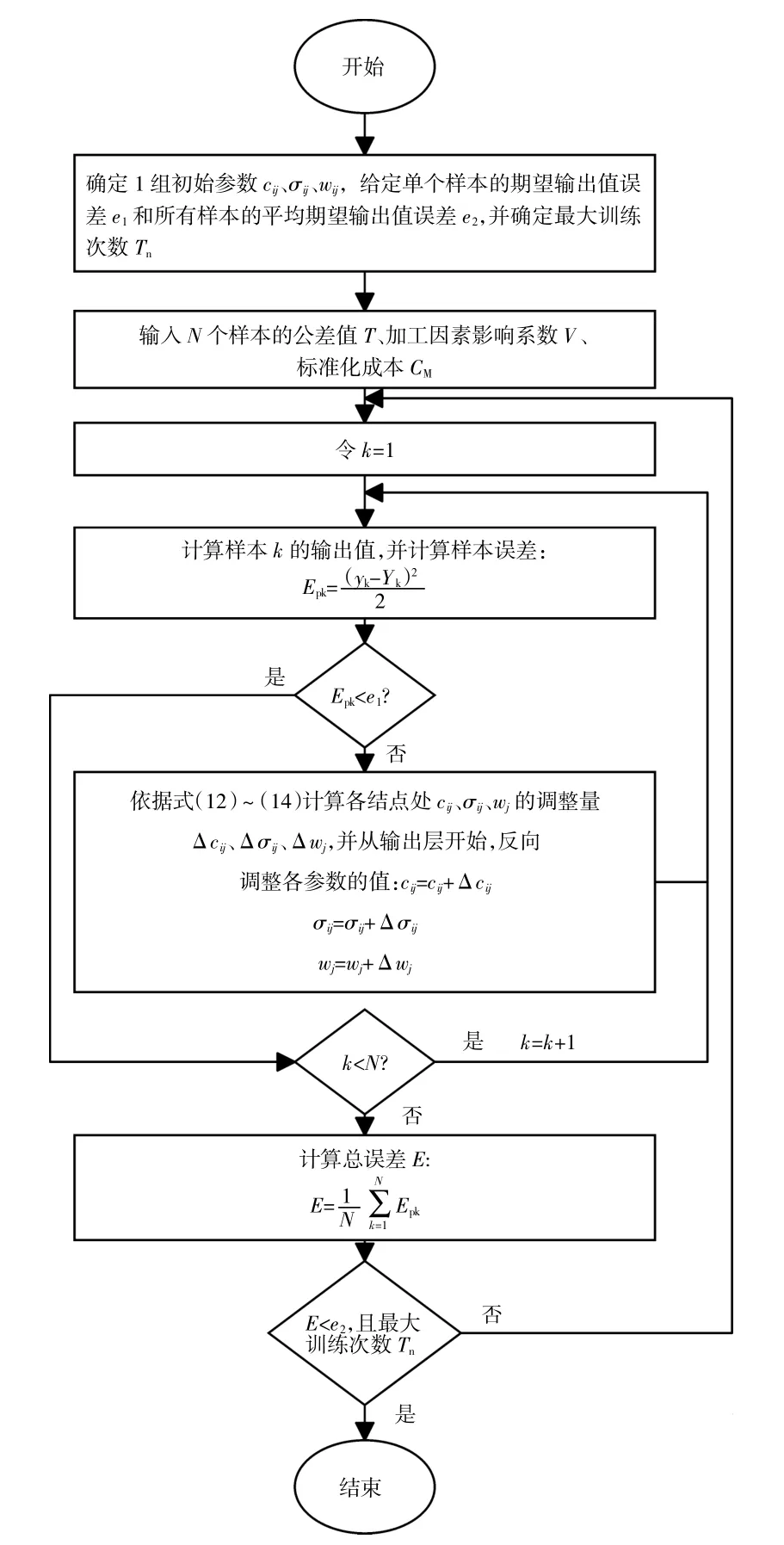
图5 模糊神经网络算法流程
6 单元体质量公差综合
根据发动机方案设计结果,对与该方案相同类型的发动机单元体的实际质量进行大量测量,形成单元体质量的数据积累。采用统计学工具,得出与设计方案相同类型发动机单元体的质量统计学分布规律。例如:假设发动机整机质量M 服从正态分布M~N (μ,σ2);假设风扇单元体质量M1服从正态分布M1~N(μ1,σ12);假设压气机单元体质量M1服从正态分布M2~N(μ2,σ22);单元体Mi大量测量后经过数据分析得出其服从某种概率分布规律。
在整机质量公差分配后,综合各单元体的质量分布规律得到整机质量,完成1 次质量公差分配的迭代。蒙特卡洛[13-15]法能够较好地利用每台发动机单元体的概率分布特性,基于统计学原理给出科学的综合结果。
蒙特卡洛算法的计算流程如图6所示。
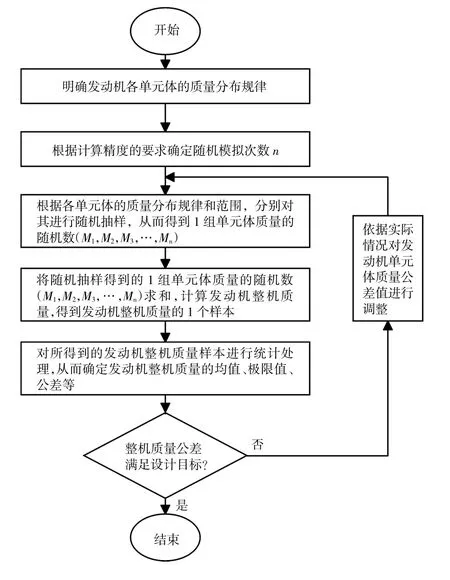
图6 蒙特卡洛算法流程
7 整机质量分配算例
以某涡扇发动机为例,分别采用现有质量分配方法和本文提出的质量分配方法开展质量分配,结果见表1。
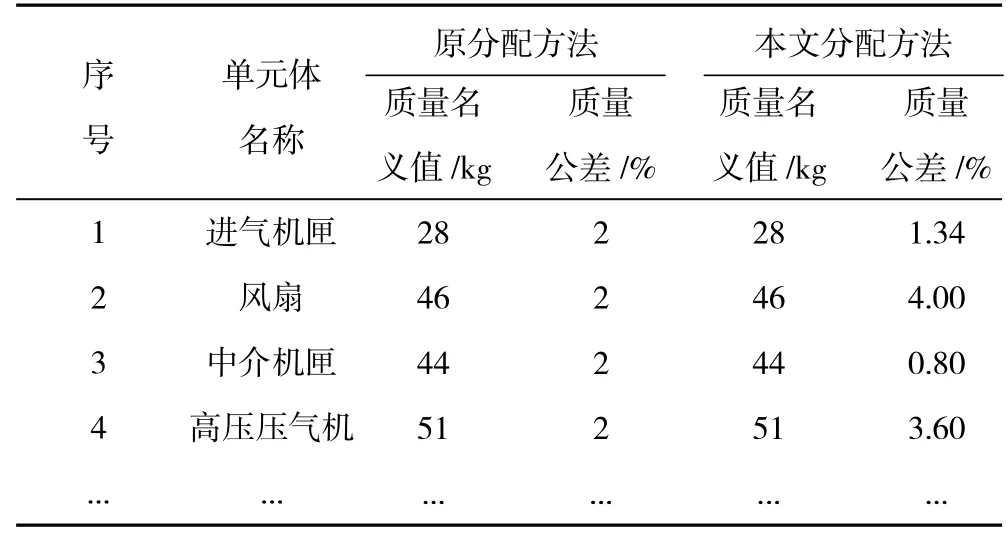
表1 质量分配结果
结果表明,本文提出的质量公差分配方法在考虑了生产成本、质量占比、零组件特性等因素后,得出了更合理的质量公差分配结果。
8 结束语
本文定义了发动机整机质量目标,提出了整机质量名义值和质量公差向单元体的分配流程和分配方法,在质量公差分配过程中重点考虑了单元体生产成本、质量占比、零组件特性3 方面因素,具有工程应用可行性和合理性。
