基于微元分析法的高压油管压力控制

刘付军，朱一波，王锦浩，杜婷伟

(1.河南工程学院 理学院，河南 郑州 451191;2.河南工程学院 电气信息工程学院，河南 郑州 451191)

高压油管被广泛应用于高压喷射的柴油机、直喷汽油机等设备，是众多燃油发动机工作的基础设施。高压共轨系统多次喷射能有效改善柴油机的排放性能和燃油经济性能， 但多次喷射时，同一喷油器相邻两次喷射的时间间隔很短，前一次喷射引起的高压油管内燃油压力波动会导致后一次喷射的油量出现偏差[1]。这种偏差将导致高压油管内的压力波动，从而对发动机的工作效率造成一定影响。

基于2019年“高教社杯”全国大学生数学建模竞赛A题,本研究针对单向阀、针阀和凸轮等因素对高压油管压力变化的影响进行了相应的探讨。在此基础上,得到了控制高压油管压力稳定所需要的最佳单向阀开启时长、最优凸轮角速度和高压油泵的控制方案。并且，根据不同情况分别建立了相应的压力稳定模型、压力渐增模型、压力守恒模型和双喷油嘴模型，然后运用微元分析法和迭代法进行求解，从而实现了高压油管压力的优化控制。

1 单向阀开启时长

1.1 压力稳定模型

单向阀的工作方式是保证介质在一定条件下只能朝一个方向流动，一旦有反向流动，介质将会被阻止。单向阀通常是自动工作的，其阀瓣打开与否由其两侧的压力差决定，阀内侧压力大于外界压力时阀瓣会自动开启，当流体反方向流动时，流体压力和阀瓣的自重作用于阀座，从而切断流动[2]。单向阀是高压燃油系统的进油控制端，所以先要对单向阀控制下的高压燃油系统进行分析。

高压燃油系统工作时，燃油经过高压油泵从A处进入高压油管，再由喷射口B喷出，工作原理如图1所示。已知喷油器每次喷油时长为2.4 ms，其喷油速率变化见图2。

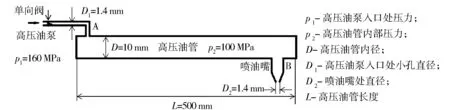
图1 高压油管工作原理Fig.1 Working principle of high-pressure oil tube

图2 喷油器喷油速率Fig.2 Fuel injection rate of injector

喷油速率函数可表述为

(1)

对式(1)进行积分可得喷油器每次工作的喷油量：

(2)

已知喷油器每秒工作10次，得到每秒的喷油量V1=440 mm3。

接下来对进油量进行计算。V2表示每秒进油量，Q表示单位时间流过小孔的燃油量，ρ表示小孔高压侧燃油密度。已知燃油的压力变化量Δp与密度变化量Δρ成正比，则某压力下燃油的密度计算公式为

(3)

式中:E=2 786.4 MPa(当压力为160 MPa时的弹性模量)；ρ0=0.850 mg/mm3(当压力为100 MPa时的燃油密度)，计算可得当压力为160 MPa时的ρ=0.868 7 mg/mm3。

当单向阀开启时，Q可表示为

(4)

式中:C=0.85(流量系数)；S=1.539 4 mm2(高压油泵A处小孔面积)。结合式(3)的结果，计算式(4)可得Q=15.378 7 mm3。

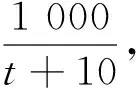
(5)

要使压力稳定，则喷油量与进油量应相等，此时建立压力稳定模型，即V1=V2。结合式(4)的结果，可得t=0.294 5 ms，即为燃油进入时每次单向阀的最佳开启时长。

1.2 压力稳定模型检验

对压力稳定模型进行检验，运用微元的思想选取一个尽可能小的周期，确保每次迭代计算得到结果的误差尽可能小。已知喷油器每秒工作10次(即每100 ms工作一次)，故选取100 ms为一个喷油周期，由单向阀开启时长t和单位时间内进油量Q可求出单向阀开启100 ms的净进油量：

(6)

在液压系统的分析和研究中通常将液压油有效体积弹性模量视为一个常量，在系统动态分析要求不高的情况下，这种简化对分析结果的影响并不显著[3]。对2019年“高教社杯”全国大学生数学建模竞赛A题所给弹性模量的数据进行3次拟合，可得

E=0.000 1p3-0.001 082p2+5.474p+1 532。

(7)

由于高压油管内部的体积不会变化，所以

(8)

结合式(8)，运用质量与密度公式求解新的压力下高压油管内部的密度：

(9)

通过拟合后的式子发现弹性模量与压力存在一定的函数关系，将式(7)、(9)代入式(3)中，可得关于仅有压力为未知量的式子为

(ρ2-ρ1)(0.000 1p3-0.001 082p2+5.474p+1 532)-ρ2(p-100)=0。

(10)

求解关于压力的三次函数，保留压力97～103 MPa作为新的压力。通过迭代上述过程的方式，依次计算在一个100 ms周期内管内压力的波动，程序流程如图3所示，压力波动曲线如图4所示。

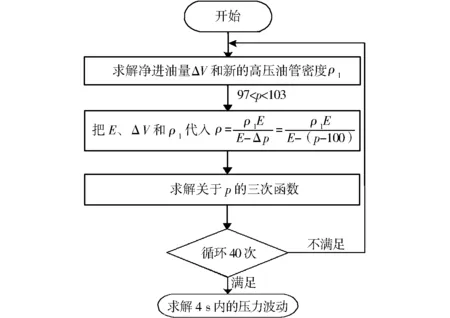
图3 程序流程 Fig.3 Program flow chart

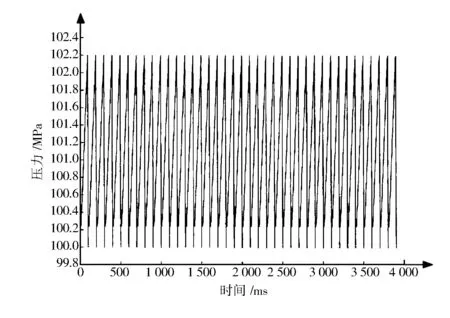
图4 压力波动曲线Fig.4 Curve of pressure fluctuation

由图4可知，当开启时长t=0.294 5 ms时，高压油管内压力在100 MPa附近波动，故建立的压力稳定模型比较合理。

1.3 压力渐增模型

当高压油管内的压力从100 MPa渐增至150 MPa时，若要进油量与喷油量相等，需要重新调整单向阀的开启时间。

在压力稳定模型的基础上，假定进油时间t1=0.294 5 ms，比较一次进油和喷油周期内高压油管的压力变化。计算一个喷油周期(100 ms)内的进油量：

(11)

当高压油管内的压力随时间变化时，对一个喷油周期前后的燃油质量进行分析，可得一个喷油周期后的燃油密度，建立压力渐增模型：

(12)

式中：ρ3表示初始压力为100 MPa时的燃油密度。

随着每次迭代，把新得到的燃油密度重新赋给ρ3以便计算下一次迭代的密度。得到一个周期后的燃油密度后，结合式(10)求解一个周期后的压力，运用迭代法，逐次增加t1的值，判断调整后在规定时间内压力能否稳定在150 MPa。 若符合，则该情况下的单向阀开启时长即为所求；若不符合，继续增加t1并迭代，直至压力稳定在150 MPa，此时t1即所求单向阀开启时长，得到的结果见表1。

表1 压力渐增模型数据结果Tab.1 Data results of pressure increasing model

表1中的计算结果表明，高压油管内的压力从100 MPa增至150 MPa，且分别经过2 s、5 s和10 s的调整过程后稳定在150 MPa，则单向阀的开启时长应分别为0.873 8 ms、0.754 0 ms和0.753 7 ms，且开启时间呈逐渐减少的趋势。

2 最优凸轮角速度

高压油泵实际组成非常复杂，由很多固件、运动件、腔室和阀体等组成，柱塞腔中的燃油在柱塞的压缩下压力升高并作用在出油阀上，出油阀腔的压力为供油管压力，当柱塞腔压力大于供油管压力时，出油阀开启，高压燃油流入供油管。因此，高压油泵柱塞腔压力及出油阀运动对系统高压管路中压力的影响较大[4]。高压油泵柱塞腔的压油过程如图5所示。

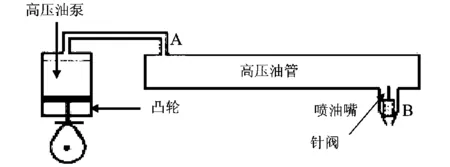
图5 高压油泵柱塞腔的压油过程Fig.5 Process of pressing oil in the plunger chamber of a high-pressure oil pump

喷油嘴的喷油量由针阀控制，针阀升程是重要的技术参数。针阀升程是否合适，会影响柴油机的性能与喷油器的使用寿命。升程太小，针阀密封锥面处的节流损失增加，压力将增大，会造成喷油器雾化不良和过载，所以针阀要有足够的升程以保证足够的流通截面和尽可能小的流动阻力，以满足柴油机的油量需要。但针阀升程也不宜过大，因为升程过大会增加喷油器弹簧的压缩量，使应力加大，易造成弹簧疲劳损坏。因此，如何在与柴油机匹配过程中确定合适的升程是非常重要的[5]。

进油时，柱塞向上运动压缩柱塞腔内的燃油，当柱塞腔内的压力大于高压油管内的压力时，柱塞腔与高压油管连接的单向阀开启，燃油进入高压油管内。喷油时，当针阀升程为0时针阀关闭，当针阀升程大于0时针阀开启，燃油向喷孔流动，通过喷孔喷出。若要保持进油量与喷油量相等，则需要分析针阀运动过程以确定凸轮的角速度。

2.1 喷油量的求解

当喷油器喷射燃油时，燃油流过的有效小孔面积与针阀运动相关且不断变化，可以通过分析针阀的运动来得到喷油量。针阀在喷油嘴中的位置如图6所示。

图6中右侧为喷油嘴和针阀的俯视图，最外侧实线表示密封座轮廓，阴影部分内侧实线表示针阀轮廓，最内侧实线表示喷孔轮廓，记阴影部分面积为S1。由图6可知，随着针阀由0逐渐上升，S1逐渐增大。当S1小于喷孔面积时，燃油流过的有效小孔面积S2=S1；当S1大于或等于喷孔面积时，燃油流过的有效小孔面积S2恒为喷孔面积。

图7为喷油嘴示意图。图7中显示了喷孔、针阀、密封座的半径和相对于密封座底部的高度。

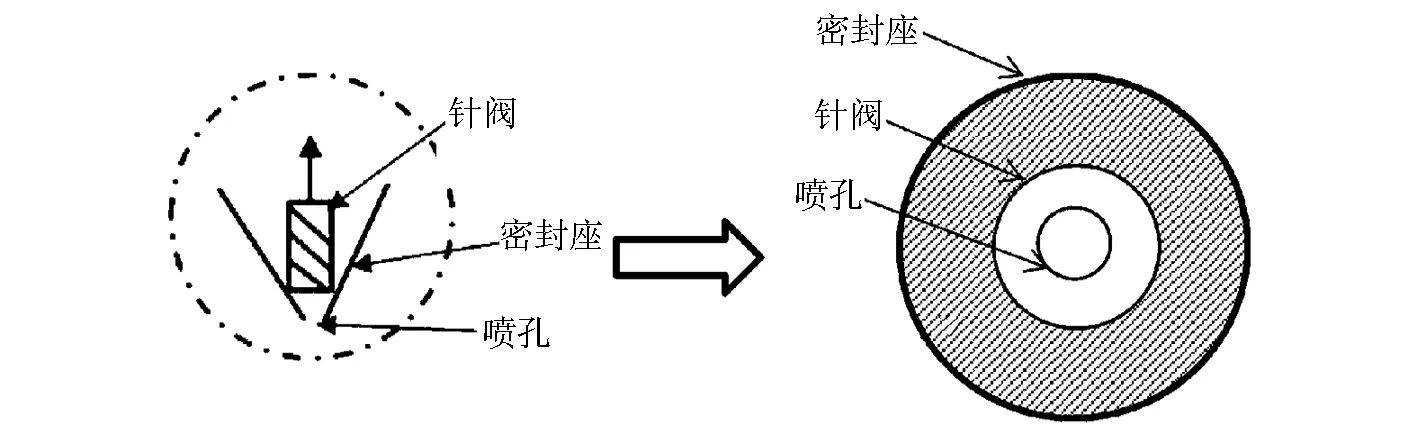
图6 喷油嘴工作原理Fig.6 Working principle of nozzle

图7 喷油嘴示意图Fig.7 Schematic diagram of nozzle parameters

(13)

又知H=h+d，由于△OBE与△CDE相似，故

(14)

已知有效小孔面积

(15)

代入式(4)，建立压力守恒模型：

(16)

结合式(10)对t进行积分，计算可得一个喷油周期的喷油量V1″=46.476 6 mm3。

2.2 进油量的求解

计算进油量时应考虑两种情况，即柱塞腔内压力达到100 MPa前和达到100 MPa后。柱塞腔内压力达到100 MPa前，由于柱塞腔内的压力小于油管内的压力，没有进油，不需要计算进油量。但在凸轮转动过程中，泵内燃油的体积改变，此时喷油嘴未喷油，质量不变，会造成泵内压力上升。当柱塞腔内压力上升至100 MPa时，柱塞腔内压力大于油管内压力，开始进油，以此为基准，计算进油量。先用微元法求取极角和凸轮的变化，以此求体积、压力和密度，再根据密度公式求出高压油管的进油量。

根据本问题中的凸轮边缘曲线，利用傅里叶函数拟合可得凸轮极径与极角的关系为

rad=4.826+2.413≠cosθ-0.000 002 676≠sinθ,

(17)

式中:rad表示极径；θ表示极角。

由于θ随时间t不断变化，故将时间划分为若干段无限小的时间段dt，则极角的微元为

dθ=ωdt。

(18)

根据所得极角代入式(17)中，与柱塞腔横截面面积相乘，即得dt时间内向油管里压缩的体积

(19)

式(19)中的柱塞腔横截面直径R1=5 mm。

对弹性模量进行如下定义[6]：

(20)

式中:V0表示压力为100 MPa时的燃油体积；dp表示压力的变化量。

由于压力变化量与密度变化量成比例，可得密度变化量，进而得到进入高压油管的油液质量。再根据密度公式，即可求得进入高压油管的油液体积。结合式(18)，给定ω初始值，进行迭代，控制喷油量V1″与进油量V2″尽可能相等，求得当柱塞腔内压力达到100 MPa时，凸轮最优角速度为0.029 7 r/ms。

3 结语

以传统的泵-管-嘴系统的高压油管为基础，运用微元思想对工作原理涉及的重要参数进行微元化处理。结合约束条件，求解出一定范围内相关参数的最优解，其结果可以运用在新一代电控燃油喷射和高压油管共轨式电控燃油喷射等系统中。