含高渗透率分布式电源的节点负荷预测方法
2020-09-15林梅芬潘文霞
林梅芬,潘文霞
(1.福建水利电力职业技术学院 电力系,福建 永安 366000;2.河海大学 能源与电气学院,江苏 南京 211100)
近年来,分布式光伏发电逐步渗透到社会各领域中[1]。配电层光伏发电的接入一方面可以减少配电网的压力,另一方面使得能源得以充分利用。如果未来光伏发电得到普及,那么我国的负荷调度将越来越需要把光伏电源这一不可忽视的因素考虑进去,同时选择精度较高的含高渗透率分布式电源的负荷预测方法,以合理安排负荷出力计划,实施常规电源和光伏发电的协调调度,提高电力生产的经济效益[2-4]。
目前,国内关于接入分布式光伏发电的高渗透率节点负荷预测文献几乎是空白。要想准确预测节点调度负荷,首先需要对光伏出力进行合理预测,尤其是高渗透率分布式光伏节点负荷的预测。短期光伏出力预测根据预测过程可分为直接法和间接法[5-6]。直接预测法是利用光伏功率历史数据及天气预报数据直接进行预测;间接预测法是先预测地表或光伏接收的太阳辐照强度,再利用神经网络或工程计算公式预测光伏功率。光伏功率预测方法大部分采用统计分析和神经网络预测方法[7-9]。文献[10]提出了一种双层神经网络单步光伏预测方法,将单层神经网络拆分成双层神经网络,基于统计分析,将天气因素整合到模型的输入端,简化了网络结构,但模型适应性不高且预测精度较低。文献[11]提出了一种基于灰色系统校正的小波神经网络光伏预测模型,考虑了相似日和相邻日之间的关系,建模过程较为复杂,个别时刻的预测误差较大。文献[12]建立了基于BP神经网络的光伏发电短出力预测模型,该模型考虑了天气类型指数,具有较高的预测精度和较强的适用性,但没有涉及具体节点,针对性不强,同时也没有对配电网的调度进行预测。本研究依据各节点的负荷特性,提出了基于小波神经网络[13]和Elman神经网络[14]相结合的方法进行含高渗透率分布式电源的节点负荷预测。
在此主要研究居民用电节点、商业用电节点和工业用电节点3类节点。查阅相关资料[15-17]并根据其负荷特点绘制各节点的典型负荷曲线。在光伏功率预测中,采用小波神经网络和Elman神经网络相结合的方法,利用历史数据及天气指数直接进行光伏功率预测,既简化了建模过程,又具有较高的预测精度。各节点所对应的光伏功率分布,按照实际节点光伏配比进行配置。最后,根据各节点的实际用电负荷及接入的分布式光伏所提供的用电负荷,得出含高渗透率分布式电源的节点预测负荷。
1 各节点典型负荷特性
分析3类节点的典型负荷曲线,依次为居民用电、商业用电、工业用电。其中,居民用电只考虑平房(农村平房及城市别墅区)这种能充分利用光伏电源的用户,商业用电负荷以商业街的商场用电为主,工业用电数据选取每天不间断工作的钢铁制造重工业的负荷数据。

图1 居民用电典型日负荷曲线Fig.1 Typical daily load curve of residents
以江苏省连云港市2015年3月份日用电负荷为例,根据其历史数据进行拟合,得到3月份居民用电典型日负荷曲线,如图1所示。
由图1可得出居民用电负荷曲线的特征,即中午和晚上为每天的用电高峰,晚上10点之后受家用洗衣机、热水器、空调等大功率电器的影响,用电量达到一天中的高峰,其余时间用电负荷相对较少。该典型日负荷曲线与居民正常上下班等活动的实际情况较为吻合。
商业用电典型日负荷曲线如图2所示。
从图2可以看出,商业用电特点为下午用电负荷持续升高,用电高峰时间一般为晚上8点,此时商场中的顾客流量达到了一天中的最大值,其负荷特性和趋势均符合商场营业规律。
工业用电除了指定节假日,几乎全年无休,全年负荷大致相同,其典型日负荷曲线如图3所示。
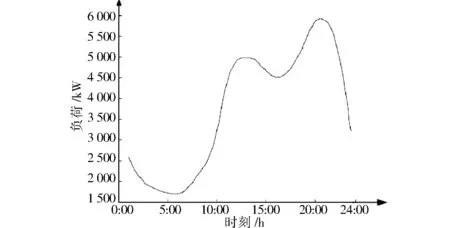
图2 商业用电典型日负荷曲线Fig.2 Typical daily load curve of business

图3 重工业用电典型日负荷曲线Fig.3 Typical daily load curve of heavy industry
由图3可以看出,重工业的用电负荷相对于其他几类而言大了许多,且因工作需要,设备大多处于常开状态,所以每天的用电负荷波动较小,相对稳定。
上述3类节点典型负荷的特性表明,各节点的典型日负荷曲线之间有着较为显著的差别,并符合实际规律,这使得对接入光伏后的节点负荷预测研究变得更有意义,并可对之后的光伏配置进行更加合理的安排。
2 基于小波神经网络和Elman神经网络的光伏预测方法建模
要想准确预测节点调度负荷,需要对光伏出力进行合理预测。光伏出力受到气象、地理等多个变量的影响,具有非线性和不确定性,很难建立非常精确的模型。因此,首先要考虑基于天气指标的小波神经网络预测方法。小波分析具有时频局部特性和聚焦特性,能够有效提取信号的局部信息,神经网络具有自学习性、自适应性和鲁棒性,小波神经网络同时具备两者特点,有很强的学习能力且精度更高[18]。而由于小波神经网络不能预测用作训练数据的前p个节点,故接下来结合Elman神经网络计算量小、速度快的优点,采用基于梯度修正的小波神经网络及Elman神经网络相结合的预测方法,选取相似天气类型的历史数据作为神经网络的训练样本,采取类似于BP神经网络的权值修正算法,旨在更准确地对第二天24 h的光伏负荷进行预测。
本研究拟预测次日各时刻的光伏出力,故先将每天分为n个时间点。小波神经网络的输入层为当前时间点的前p个时间点的负荷,输出层为当前时间点的预测光伏负荷,则小波神经网络预测的光伏负荷为预测日(n-p)个时刻的数据。Elman神经网络计算量小、预测精度较高,可用来预测前p个时刻的光伏负荷。
2.1 小波神经网络
小波神经网络是一种以BP神经网络拓扑结构为基础,把小波奇函数作为隐含层节点的传递函数,信号前向传播的同时误差反向传播的神经网络,其隐含层的输出计算公式为
(1)
本研究采用的小波基函数为Morlet母小波基函数,数学公式为
(2)
小波神经网络输出层计算公式为
(3)
式中:h(j)为第j个隐含层节点的输出;hj为小波基函数;ωij为输入层和隐含层的连接权值;bi为小波基函数的平移因子;ai为小波基函数的伸缩因子;y(k)为神经网络的第k个输出;ωjk为隐含层到输出层的权值;n为输入层节点数;l为隐含层节点数;m为输出层节点数。
小波神经网络修正过程如下:
(1)计算网络预测误差

(4)
式中:yt(k)为期望输出;y(k)为小波神经网络预测输出。
(2)根据预测误差e修正小波神经网络权值和小波基函数系数:
(5)
(6)
(7)
(8)
(9)
(10)
式中:η为学习速率。
2.2 Elman神经网络
Elman神经网络是一个具有局部记忆单元和局部反馈连接的递归神经网络。它的主要结构是前馈连接,包括输入层、隐含层(中间层)、承接层和输出层。其中,隐含层的输出被输送到承接层,承接层在接收到信号后再将上个时刻的隐含层输出和当前时刻的网络输入一起反馈到隐含层的输入端。这种自联能使网络对历史数据充分训练,而且可以逼近任意非线性映射。Elman神经网络的非线性状态空间表达式为
y(k)=g(ω3x(k)),
(11)
x(k)=f(ω1xc(k)+ω2(u(k-1))),
(12)
xc(k)=x(k-1),
(13)
式中:y为m维输出节点向量;x为n维中间层节点单元向量;u为r维输入向量;xc为n维反馈状态向量;ω3为中间层到输出层的连接权值;ω2为输入层到中间层的连接权值;ω1为承接层到中间层的连接权值;g(*)为输出神经元的传递函数,是中间层输出的线性组合;f(*)为中间层神经元的传递函数。
Elman神经网络的权值修正也与BP算法类似,其学习指标函数的表达式为
(14)
2.3 影响因子指数
光伏出力受外界环境的影响较大,故本研究通过光伏发电历史数据与这些影响因素之间的关系映射成天气类型指数,对天气类型进行划分,作为神经网络的另一个输入量。
根据文献[19]对天气的划分,可将天气从广义上分为4类:晴天(晴、晴转多云、多云转晴)、阴天(阴、雾、霾)、多云(多云、多云转阴、阴转多云)、雨天(小雨、中雨、大雨、暴雨、雷阵雨、小雪、中雪、大雪)。
对比连云港地区光伏发电功率数据及所在位置的气象数据可以发现,不同天气类型的光伏发电功率曲线差别较为明显。将该地区4类典型天气光伏发电曲线进行对比(见图4),时间间隔为15 min。
由图4可以看出,在4种不同天气下,光伏发电具有明显差别,晴天较为理想,雨天、多云、阴天受阳光的影响,曲线波动较大,尤其是雨天的有效负荷较晴天而言明显下降。因此,在光伏功率预测中,天气是不可忽视的影响因素,天气类型划分也显得尤为重要。
将4种天气类型光伏发电数据之间的倍率关系以数值显示映射为天气类型指数。4种天气类型的光伏平均发电功率关系如图5所示。

图4 4类典型天气光伏发电对比Fig.4 Comparison of photovoltaic power generation in four typical weathers
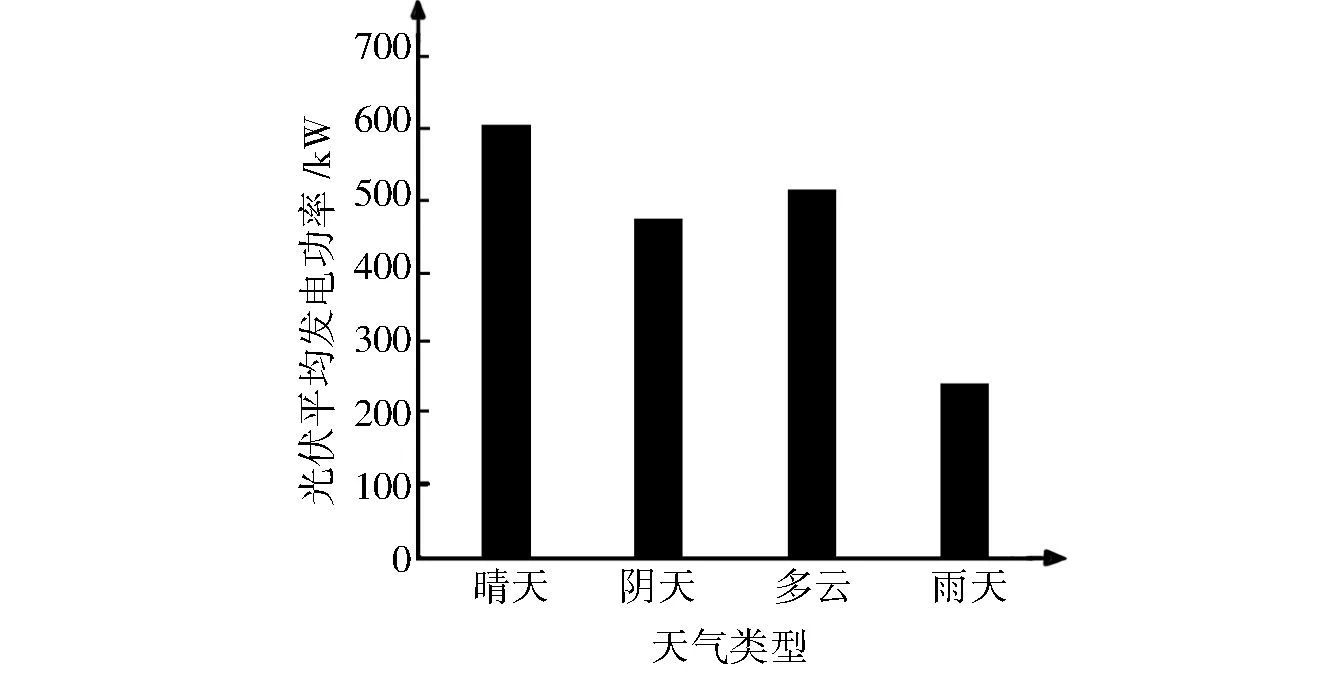
图5 4种天气类型的光伏平均发电功率关系Fig.5 The relationship of average power generation and the four types of weather
由于晴天的光伏发电量是所有天气类型中最大的,故将晴天的天气指数设为1,按照倍率关系将其映射为天气指数,作为神经网络训练的一个输入量。4种天气的天气类型指数如下:晴天为1,阴天为0.78,多云为0.85,雨天为0.40。
3 算例分析
选用江苏省连云港市2015年的光伏发电数据和该地区部分居民用电(以平房为主)、商业用电(以人流量大的商场为主)、工业用电(重工业)的实际用电数据。首先运用上述光伏预测模型对光伏出力进行预测,测试模型的可行性与预测精度,再根据各节点的实际用电负荷分别绘制各研究节点的统调负荷曲线,即介入光伏后配电网发电的预测负荷。
3.1 光伏预测结果
首先选取3月份的一个星期共7天,每隔15 min采集一次数据(光伏实际负荷),每天共96个数据,对前6天的数据进行小波神经网络训练,第7天的数据作为测试样本,从而利用训练好的神经网络对第7天的光伏负荷进行预测。本次预测采用的小波神经网络输入层为当前时间点的前4个时间点的负荷,即4个节点,输出层有1个节点,表示网络预测的负荷,这样可以预测从第5个时间点到第96个时间点的光伏负荷。
第2天的光伏负荷前4个时间点采用Elman神经网络预测。同样选取一个星期的前6天,每天前4个时间点的光伏负荷数据作为训练样本,每3天的负荷作为输入向量,第4天的负荷作为目标向量,得到3组训练样本,第7天的数据作为测试样本,验证所建网络的可行性。

图6 光伏预测曲线Fig.6 PV prediction curve
光伏预测结果如图6所示。从图6可以看出,光伏预测曲线与测试曲线基本吻合,表明预测模型具有可行性,预测精度也较高。
3.2 各节点统调负荷
光伏发电功率按平均每平方米150 W进行计算。对于居民用电和工业用电而言,主要考虑多以平方米为主的居民区和工业厂房,故光伏占面积比相对较大;对于商业用电而言,考虑到商业区多为高楼,即使未来光伏可安置于商业幕墙中,光伏所占面积比也相对较低。
综上所述,按照每节点日均用电量与光伏最大输出功率计算其光伏配比:居民节点为1.5∶1、商业节点为1∶4、工业节点为1∶2。
根据上面对光伏负荷预测(Sv)的结果与各节点实际用电负荷(Sa),可得各节点的统调负荷(Sc),计算公式为
Sc=Sa-Sf。
(15)
考虑到光伏发电在晴天的状态较为理想,本研究以晴天为例,计及光伏的居民用电负荷曲线如图7所示。从图7可以看出,当居民的光伏配比为1.5∶1时,中间有一段时间的统调负荷为负数,表明这段时间内光伏除了给居民供电,还给配电网输送电。
计及光伏的商业负荷曲线如图8所示。从图8可以看出,由于商业用电的高峰集中在傍晚至晚上,且光伏配比较为不理想,没有其他节点的光伏配比高,所以光伏发电所能抵用的用电负荷相对较少。
计及光伏的工业负荷曲线如图9所示。从图9可以看出,由于工厂可供安装光伏的面积较大,所以在一段时间内,光伏能够提供给工厂的电量很多,虽然不能像居民统调负荷中出现的光伏发电情况,但在一定程度上减轻了白天用电高峰的供电压力。
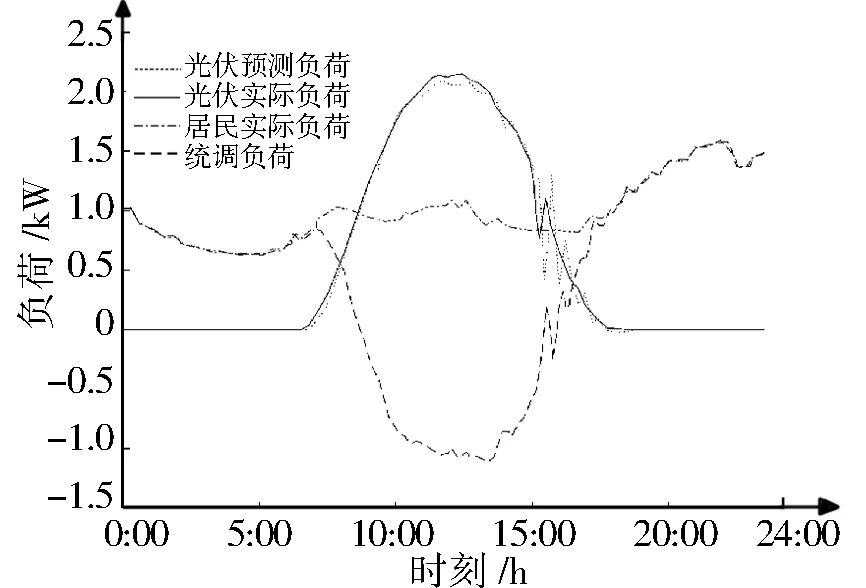
图7 居民统调负荷曲线Fig.7 Regulation load curve of residents
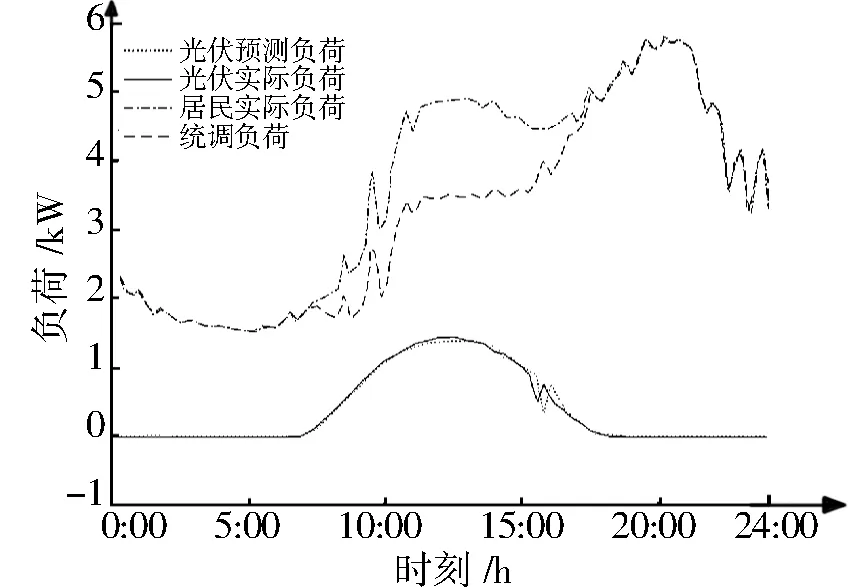
图8 商业统调负荷曲线Fig.8 Regulation load curve of business
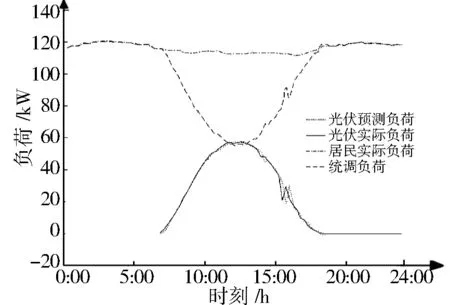
图9 工业统调负荷曲线Fig.9 Regulation load curve of industry
3.3 总统调负荷
考虑到同时率问题[20],所有节点的实际负荷都要按照一定比例汇总,系统负荷同时率计算公式如下:
(16)
式中:Pm为系统最大负荷;Pm1,Pm2,…,Pmn为系统中各个用户的最大负荷。
由文献[21]可得各节点的同时率:居民节点为0.2,商业节点为0.8,工业节点为0.94。
将所有节点的负荷汇总之后,计及光伏的总负荷曲线如图10所示。由图10可以看出,光伏的接入可在某段时间内大大减轻配电网负荷配送的压力。
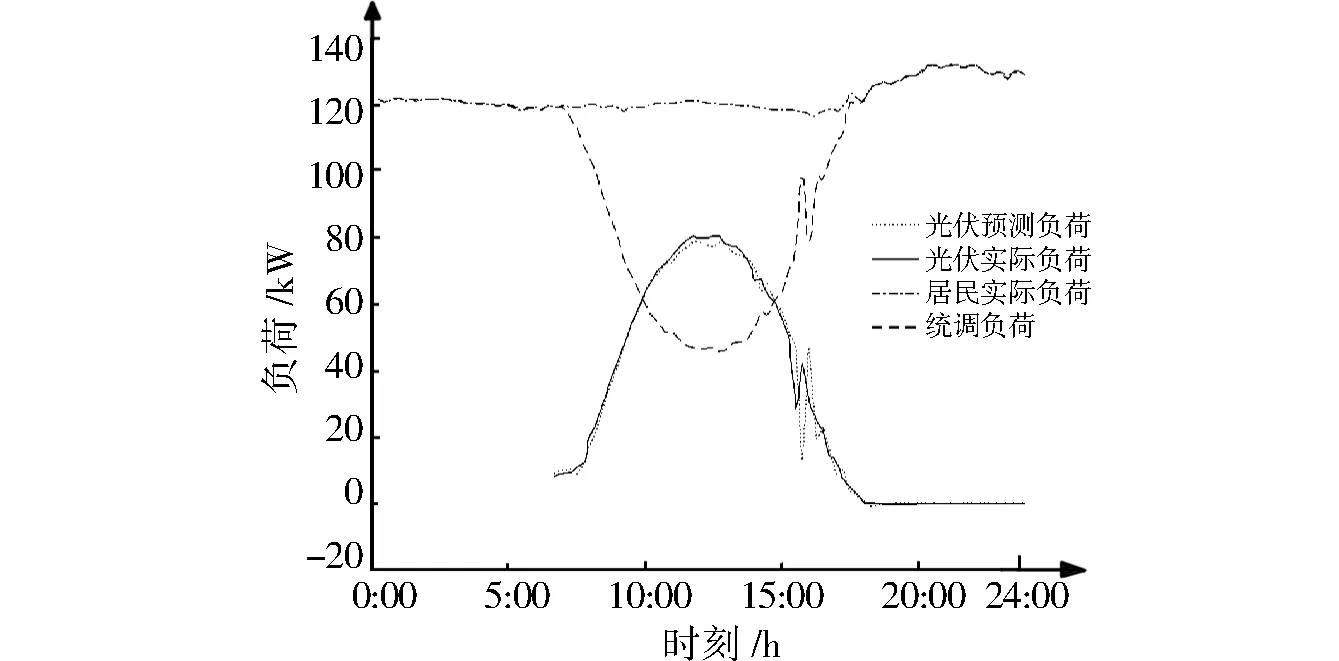
图10 总统调负荷曲线Fig.10 Regulation load curve of residents
4 结语
本研究提出了一种含高渗透率分布式电源的节点负荷预测方法,与传统负荷预测相比,在光伏负荷预测方法上进行了改进,采用计及天气指数的小波神经网络与Elman神经网络相结合的预测模型,对光伏出力进行了有效预测,预测精度较高。通过分析处理居民用电、商业用电、工业用电3个节点的实际用电负荷和分布式电源所提供的负荷,最终对各节点的统调负荷做出有效安排,未来分布式光伏得到广泛运用时,配电网能够及时对各节点负荷进行较为精准的配送。
