“工程数学”之“数值分析”课堂教学改革的实践与探讨
2020-09-15高翠侠
高翠侠
(江苏大学理学院 江苏·镇江 212013)
0 引言
随着2017 年新工科建设的提出,“工程数学”的地位进一步加深,使得对这门课的教学要求也提高了。“工程数学”是针对工科学生开设的运用数学理论处理实际工程问题的专门课程,此课程普遍由多门数学子课程组成,比如矩阵论、概率论与数理统计、数值分析、复变函数等。数值分析(Numerical Analysis)不同于其他子课程,其应用性更强,重在教授学生如何运用数值计算方法解决实际问题,强调学生的自主性、探索性、合作性和研究性。同时,不同于本科教学,研究生的数值分析教学更注重于学生能力的培养。
数值分析教学的目的在于计算理论方法的掌握和解决问题的实践能力的培养,是数学计算与工程的结合、理论性与实践性的结合,为学生各自领域的科研,甚至是以后的工作打下必要的基础。而对于“工程数学”中数值分析的教学,教学内容多、课时少、难度大是普遍存在的问题,[1,2]加之学生前期所学数学基础参差不齐,致使教学效果欠佳。因此,应该如何运用有效的课时对教学内容进行优化,使得教学效果达到最高,是每一位任课教师需要思考的问题。
1 学情分析
江苏大学(以下简称“我校”)的研究生“工程数学”课程是依托车辆工程、动力工程、材料工程、机械工程、光学工程、仪表仪器工程、建筑与土木工程等工科专业硕士研究生的学位课。学习群体涉及多个专业,同一专业也会涉及众多的研究方向,这就对课堂上应用案例的选择和讲授提出了一定的挑战。而首要的问题是对历届选课学生的专业背景、学术研究中所涉及数值计算方法等情况进行统计分析。“工程数学”在各行各业的实际应用很多,通过对近几年本人所授工科研究生学生的毕业论文进行统计,涉及2018-2019 届300 多篇论文,聚焦得到的核心词汇见表1。

表1 所研究样本中涉及数值计算知识点的统计分析
2 教学存在的一些问题与改革措施
2.1 对教师工科背景知识理解的要求
对学生学情的掌握是首要问题,而接下来的问题就是教师如何实施自己的教学。教学的进一步实施离不开教师对工科背景知识的了解,即教师自身专业素养的提高。而工科背景缺乏是数学教师普遍存在的问题之一。教师自身专业素养的提高包括:将自己的科研与工科教学相结合、更新教学素材、关注学科前沿等等。通过教学,不仅能使学生掌握基本理论,还能缩短基础知识与学科前沿的距离,调动学生的学习兴趣。
作为数学教师,不能局限于数学学科的精通,还需要对工科背景或者基础理论知识有一定的掌握和思考,把各学科之间的联系融入到你的课程中来。以如下一个具有突起的开槽里流体流动的伯努利方程[3]为例,
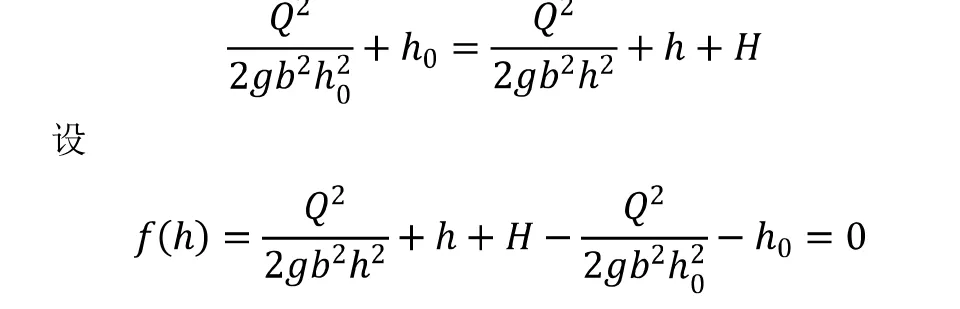
问题就转化为利用迭代法求解非线性方程 的根
。首先绘制 函数图像以确定根的大致区间,要求精度(绝对误差) ,最大迭代次数 。此时,可以分别使用二分法、牛顿法和弦截法对方程组进行求解并进行对比。以上所讲的都是数值计算的问题,而作为教师,还要明确关于伯努利方程的背景、方程中各参数的含义以及彼此之间的作用关系等等。了解“伯努利原理”是1726 年由丹尼尔伯努利提出的,是在流体力学的连续介质理论方程建立之前,水力学所采用的基本原理;了解其实质是流体的机械能守恒:动能+重力势能+压力势能=常数;了解实际应用案例有喷雾器、汽油发动机的化油器、兵乓球的旋转等等。
2.2 明确实践能力培养的教学目标
我校研究生“工程数学”课程由矩阵论、概率论与数理统计、数值分析三门子课程组成,共36 课时。数值分析占“工程数学”总课时的三分之一,共12 课时,具有典型的内容多、课时少特征。从而对数值分析教学内容的选择、教学模式、考核方式等都提出了挑战。
(1)教学内容选择。内容的选择依赖于教学的目标,“数值分析”作为理工科专门开设的一门课程,涉及内容广,通常包括函数插值与数值逼近、线性与非线性方程(组)求解的数值方法、常微分方程求解等,具有理论证明或推导繁杂、难度大、缺乏应用案例分析的特点。而“工程数学”中的数值分析不同,其致力于学生解决工程问题能力、实践能力的培养。因此,在教学内容选择时,需摆脱“重理论、轻实践”的传统教学模式,即“重原理分析、轻证明推导”“重案例式教学、轻课堂讲授”“重交互实验、轻理论灌输”。
(2)“理论讲授-案例教学-小组研讨”的教学模式。传统的教学模式主要以理论知识讲授为主,缺乏与实际问题的联系,缺乏因实际问题解决而产生的生-生、师-生之间的互动,这不利于学生分析和解决问题能力的培养,更不利于新工科人才的培养。既然“工程数学”课程以实践能力培养为教学目标,那么就在一定程度上决定了教学的方式。工程教学案例的引入,能够让学生更加清楚所学的数值计算方法在自己的领域中如何用、用在何处,真正做到从实际中来再应用到实际中去。教学实践表明:案例教学以及小组专题研讨,有利于提高研究生对本课程的学习兴趣,有利于提高研究生的工程应用能力、创新实践能力和学术研究动力。
(3)综合的评价与考核机制。数值分析内容涵盖较广、综合性较大,期末试卷上不能涵盖所有知识点。既然教学内容和方式在逐步地改变,那么课程的考核方式也应随之而变化。本课程的定位是培养新工科建设人才,而学生的成绩评价是一个重要的环节,传统的闭卷考核方式已不能完全符合新工科人才培养的需求。[4]在通过卷面考试评价学生基础理论知识学习掌握程度的基础下,还需创新考试方式,注重考核学生的实际编程能力和应用能力,比如可以将参加数学建模竞赛的成绩作为期末成绩的参考标准之一。另一方面,充分利用课堂上所采用的教学案例,教学案例的讲解一般是伴随着程序的编写,此时,可以让学生通过调节部分参数得到新的设定的结果,以培养学生的实际操作能力,这也可以作为期末成绩的考核标准之一。
3 打通不同课程之间的壁垒
数值分析部分的教学要注意与不同课程间的壁垒。首先,是与已有相关数学或非数学专业知识的衔接。作为工科课程,需要修高等数学、线性代数和数学软件等课程。为了帮助学生加深对知识点的理解和掌握,需帮助学生将重要的相关知识点进行整合,厘清彼此之间的关系,形成一个整体的知识结构框架。例如,在线性方程组求解常用的直接法和迭代法的讲解之前,先回忆以前学过的求解方程组的方法有十字相乘法、Gramer法则等,其中Gramer 法则线性代数中的一种重要的方程组求解判定法则,具有收敛、稳定、结论可靠的有点,但是其缺点是计算量大。此外,还要注重教学内容与学生正在学习的专业课程的相互呼应。
此外,要注重与理工科“数值分析”课程教学侧重点的区别。除了“工程数学”中的数值分析教学内容外,我校还开设了专门的针对理工科研究生的“数值分析”课程,并且数值分析是很多高等院校理工科专业的必修课程。[5]理工科的“数值分析”课程涉及数学分析、代数、微分方程等众多数学学科,要求学生修过数学分析、高等代数等基本学科,即具备扎实的数学理论基础。对于“工程数学”中的数值分析课程而言,同样需要学生具有以上多个数学学科基础,但是不乏有学生同时选修“工程数学”和“数值分析”两门课程,此时就要注意区分教学侧重点。比如,理工科“数值分析”课程较多地注重定理的证明、计算公式的推导,容易与应用脱节。本课程的教学则要更加注重对案例的讲解、借助信息化技术提高学生的体验感、设计交互实验增加学生的实践能力,同时,对于有些理论推导证明可以省略,留给学生课后去阅读。
最后,还要明确与矩阵论和概率统计课程之间的地位与作用。传统的“工程数学”课程体系不系统,多是分别对不同模块内容进行讲解。[2]
4“线上教学”下本课程的机遇
为了落实教育部和学校关于“停课不停教、停课不停学”的政策,高校教师纷纷将教学搬到线上进行,数学类课程也不例外。数值分析本身就是面向计算机、强调实践性的课程。在线下教学时就采用应用案例教学设计与信息技术相融合的教学方式,但是总未充分发挥学生参与实验的作用,比如教室投影设备中没有数学类软件等。“工程数学”课程所涉及的常用数学软件有MATLAB,Python,Lingo,Mathematica 等。教学软件的模拟仿真、动画展示能够让学生产生直观的体验,特别是面对复杂的定理和推导公式时。

图1 不同插值方法和拟合图形的绘制
线上教学无疑给案例教学、交互实验等课堂活动带来机遇。在疫情下,应积极构建信息化的、立体化的教学手段和教学资源,增加学生在课堂中对工程案例实现过程的体验,打破时间和空间限制。
实验1 不同插值曲线的绘制以及与曲线拟合的比较。
在讲授插值法和曲线拟合内容时,可以借助MATLAB 软件,让学生参与运行和修改程序,体验不同插值方法结果的差异性。程序1 实现了不同插值方法下插值曲线的绘制,以及同一实验数据下拟合曲线的绘制。图1 给出了实验结果。观察实验结果,学生不仅可以清楚地了解插值与拟合的区别,还能对分段线性插值、三次样条插值等不同差值方法、外插风险、误差等概念有直观和深入的理解。当然,这就要求学生在掌握算法的同时,还要熟练掌握和运用计算机编程语言。此外,基于这样一个简单的实验,可以随堂给学生布置小组任务,每一个小组要求提供出一组研究领域相关的实验数据,拟合出一条曲线,使得这个曲线与原始数据间的误差最小。
程序1 不同插值及拟合曲线的多子图绘制
clc;clear all;
x=1:1:10;y=[15 12 17.5 17 22 16 15.5 14 12 13];
subplot(1,2,1)
xx=1:.25:10;yy=interp1(x,y,xx);plot(x,y,'kd',xx,yy)
hold on;yy=interp1(x,y,xx,'nearest');plot(xx,yy)
hold on;yy=interp1(x,y,xx,'spline');plot(xx,yy)
subplot(1,2,2)
plot(x,y,'kd')
hold on;polyfit(x,y,4)
5 结束语
针对传统研究生“工程数学”中“数值分析”教学模式中存在的课时少、内容量大、缺少交互实验等弊端,本文从学生层面、教师层面进行分析,并从教学内容、教学模式、评价机制三个方面做出改革建议,打破传统的以基本理论为主而忽略学生实践能力、分析和解决实际问题能力培养的教学模式,更好地发挥出“工程数学”这门课程的重要作用。此外,在新冠疫情下,线上教学给学生带来了全新的体验。本课程应充分发挥其面向计算机这一特点,积极提升信息化、多元化、立体化的教学模式与资料,促进学生的学习动力和乐趣,有助于应用型人才、复合型人才的培养。
