基于下垂控制的微电网建模与仿真

2020-09-14聂晓华高家明

实验室研究与探索 2020年8期

聂晓华，高家明

（南昌大学信息工程学院，南昌330031）

0 引言

随着新能源技术不断发展和人们环保意识的增强，以新能源为基础的微电网得到了广泛应用和推广。逆变作为新能源连接负荷的重要纽带，也是新能源发电技术研究中的重要课题［1］。

在微电网的研究中，有关并网、逆变技术的研究一直以来都是重点、难点［2］。微电网的控制技术分为：对整体微电网控制策略研究，以及对局部微电源控制方法的研究［3］。现有各类文献中，对微电源中有关于逆变器的知识多以理论分析为主，同时受实验设备限制，初学者很难在学习的过程中将理论与实践相结合。Matlab ／ Simulink 仿真平台解决了这个问题，在Simulink平台上搭建基于下垂控制原理的微电网孤岛模式仿真实验模型［4］。以微电源的下垂控制方法为背景，通过该模型了解下垂控制方法，电压、电流双环控方法。微电网孤岛模式下运行，当负荷的扰动时，解决了系统频率和微电网电压幅值支撑问题，提高了电能质量。并且本文中给出了详细的建模与仿真步骤。用仿真结果证明理论分析的正确性，激发学习者的学习热情。

1 下垂控制原理

1.1 微电网的模型

微电网模型如图1 所示，为了简化模型，微电源等效成直流电源Udc经过逆变输出的交流电源U∠δ 并传输功率到微电网的公共交流母线上。

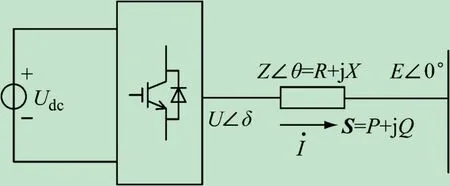
图1 微电源模型

1． 2 原理分析

图2 为微电网模型相量图，Z∠θ为微电源到公共交流母线线路上的阻抗。

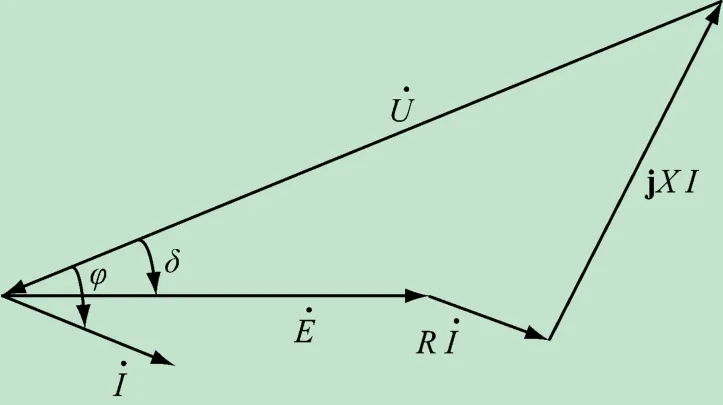
图2 微电网模型相量图

其中：R 为电阻；X 为电抗；E·为公共交流母线上的电动势相量；U·为微电源输出的电压相量；δ为E·和U·之间的夹角。那么线路上传输的复功率S可以表示为：

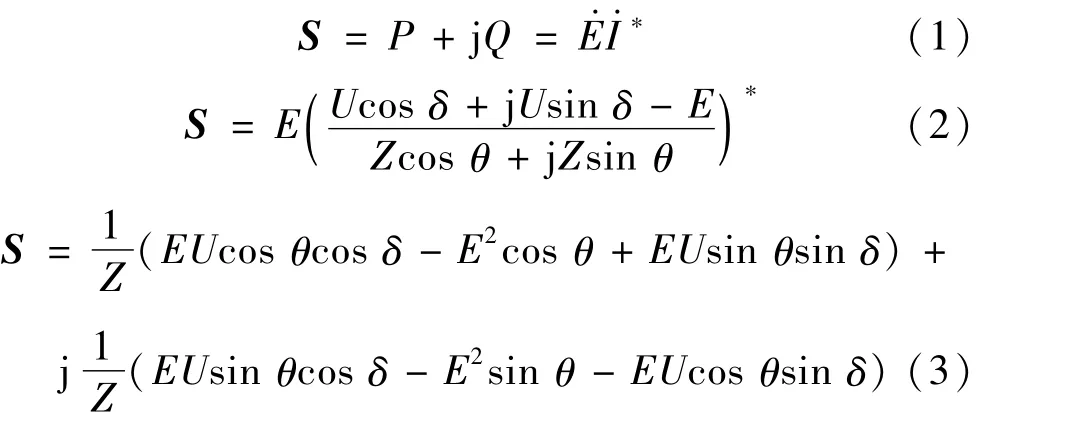
根据式（3）线路上传输的有功功率和无功功率分别为：

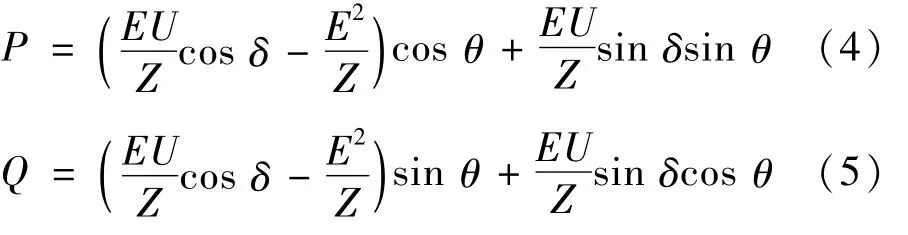
在微电网高压输电系统中，输电线路呈感性，X≥R，输电线路上电阻R相对于电抗X可以忽略不计，即

式（4）、（5）就可以分别化简为：

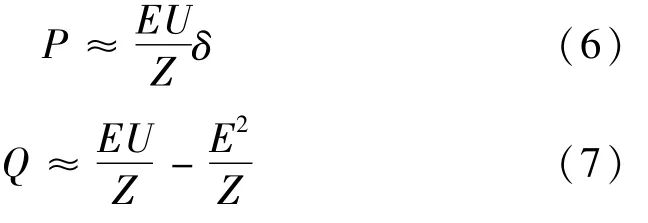
系统要求输入到微电网公共交流母线上的电压保持稳定，E·偏差很小，可以认为E 是保持不变的。在线路为感性和δ 很小的条件下，根据式（6）、（7）可知线路上微电源发出的有功功率P 和δ近似线性关系，微电源发出的无功功率Q 和电压值U 近似线性关系［5］。P主要由δ决定的，Q主要由U决定。由于

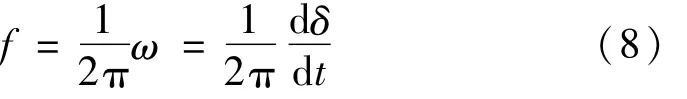
由式（8）可知，δ由系统的频率f（或角频率ω）决定。那么可以得知线路上的传输有功功率P和f的关系，P间接由f决定。

2 下垂控制设计

下垂控制原理如图3 所示，它主要由功率控制器和电压、电流双环控制器组成［6］。功率控制器主要由3 个模块组成，分别为dq 变换和功率计算模块、下垂控制模块、电压合成模块［7］。

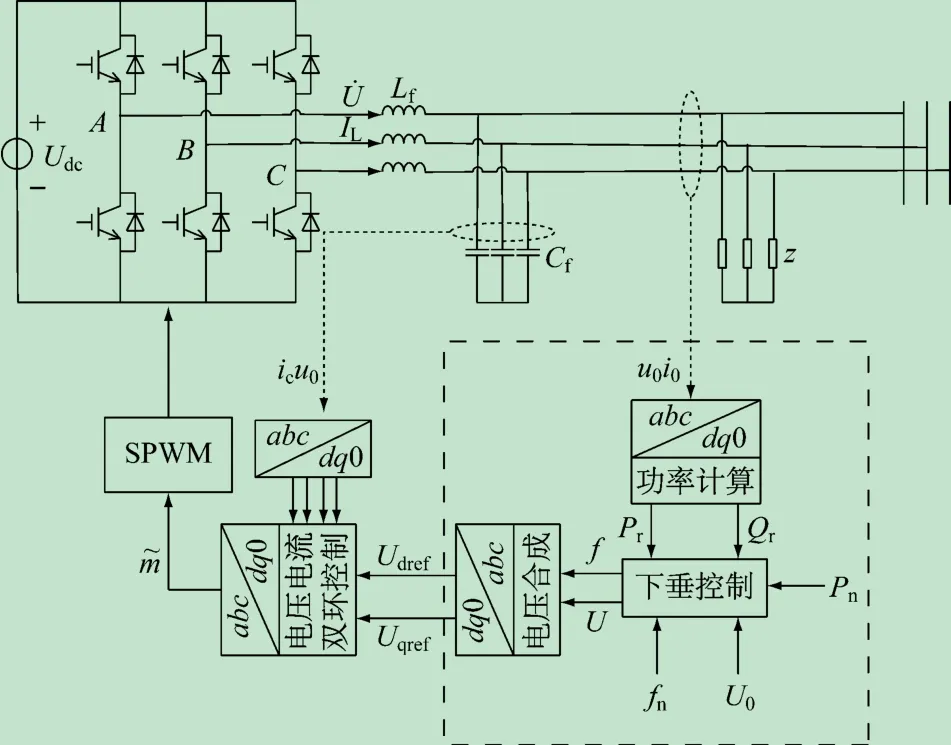
图3 下垂控制原理

功率控制器框图如图4 所示，经过LC滤波器后负载端的电流和电压经过dq变化后，其瞬时功率［8］为：

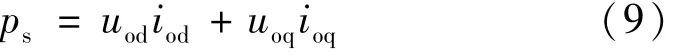
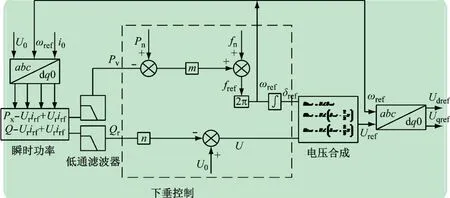
图4 功率控制器

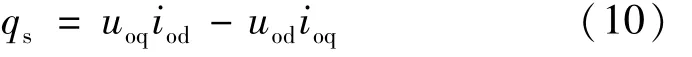
式中：ps为瞬时有功功率；qs为瞬时无功功率。瞬时功率再经过低通滤波器［9］，输出平均有功功率Ps和平均无功功率Qs。

在下垂控制器的模块中，微电源按照有功功率和无功功率给定的方式向负载传输。Pn为微电源发出的额定有功功率，fn为额定频率。U0为微电源输出无功功率为零时微电源的电压值。根据下垂控制原理得Ps- f、Qs- U关系：

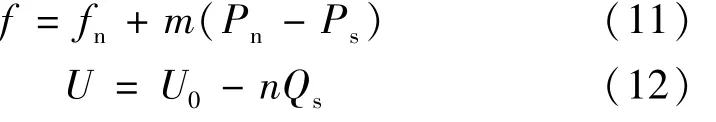
式中：Ps、Qs分别为微电源输出到负载的平均有功和无功功率；m 为Ps- f 下垂系数；n 为Qs- U 下垂系数。其中m，n表达式［10］为：

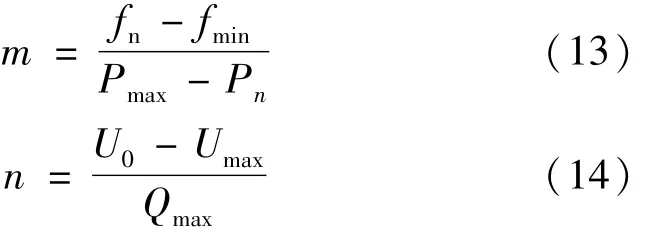
式中：fmin为微电源输出的平均有功功率最大时，系统频率根据Ps- f下垂特性下降的最小值；Pmax为微电源输出平均有功功率最大值；Umin为微电源输出最大平均无功功率最大时，微电源电压值根据下Qs- U 垂特性下降的最小值；Qmax为微电源输出的最大平均无功功率。当微电源发出的有功功率过大时，通过系统频率的增加，就会减少微电源发出的有功功率；当微电源发出的无功功率过大时，增加微电源输出的电压幅值，就会减少微电源发出的无功功率。反之亦然。通过这样合理的分配有功和无功功率，使得系统达到最小的环流点。下垂特性曲线如图5、6 所示。

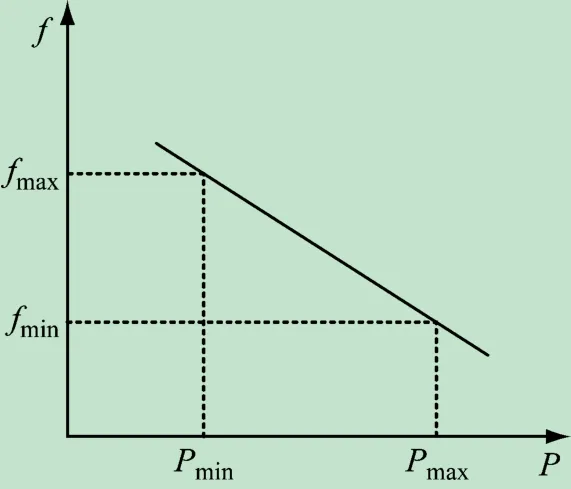
图5 Pv - f下垂曲线

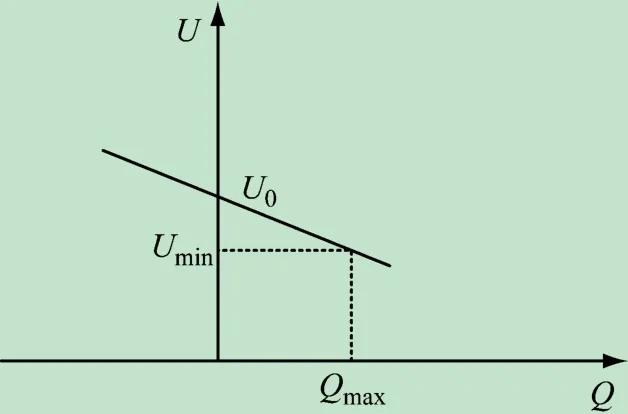
图6 Qs - U下垂曲线

微电源逆变输出和电压合成环节中的电压是随时间改变而变化的交流量，在三相静止坐标系下PI调节器无法对交流量实现零稳态误差控制，所以采用dq变换实现三相静止坐标系到两相同步旋转坐标系的变换［11］：

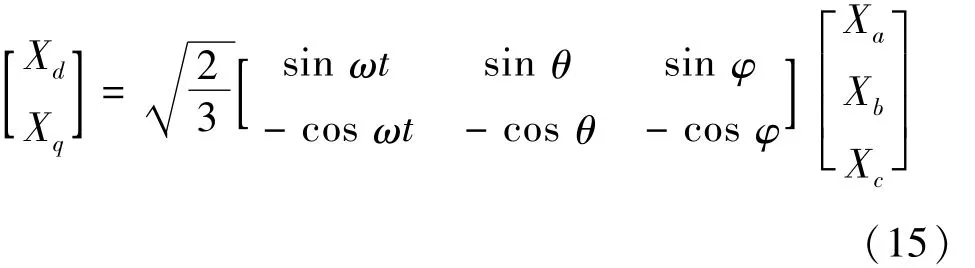
式中：θ ＝ ωt - 2π／ 3；φ ＝ ωt + 2π／ 3。

直流电源Udc经过逆变之后，采用LC 滤波［12］，电容Cf电流方程表达式为

LC滤波器中滤波电阻Rf值很小，忽略不计，则图中电感Lf电压方程表达式为

根据式（16）～（18），设计电压、电流双环控制器［14］，电容电流用于内环控制，负载电压用于外环控制，如图7 所示，该模块输出PWM控制信号。

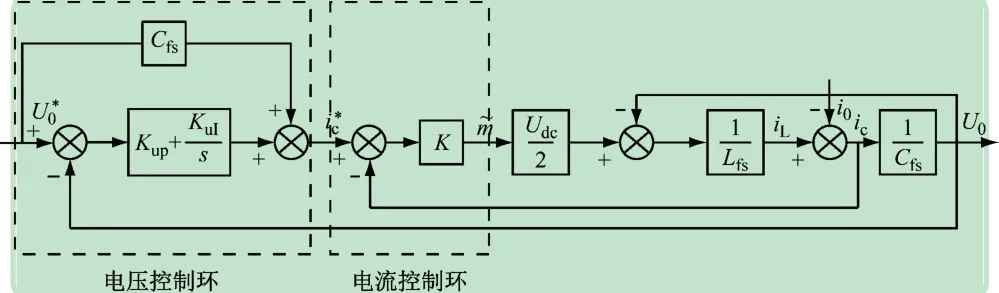
图7 电压、电流双环控制器

参考电压和负载电压的dq 轴分量作为电压外环的输入，外环控制采用PI 调节器，其中Kup、KuI分别为PID调节器中的比例和微分系数，该调节器在负荷扰动时稳定负载电压，提高负载电压的精度。外环输出作为电流内环的输入，内环采用P调节器，其中K为P调节器的比例系数，为了在负荷扰动时提高系统的动态响应速度。

3 下垂控制器仿真模型

根据上述下垂控制原理分析和控制系统的设计，可以在Simulink平台中搭建仿模型，dq 变换和功率计算模块如图8 所示。

该模块中计算得到瞬时有功功率和瞬时无功功率经过低通滤波器得平均有功功率和平均无功功率，作为下垂控制模块的输入［15］。下垂控制模块和电压合成的模块如图9 所示。

微电网系统的频率由式（11）得到，微电源的电压值由式（12）得到，同时将两者合成参考电压的相量，经过dq变换后作为电压、电流双环控制其的输入，另外，此处得到频率作为dq变换的参考频率［7］。

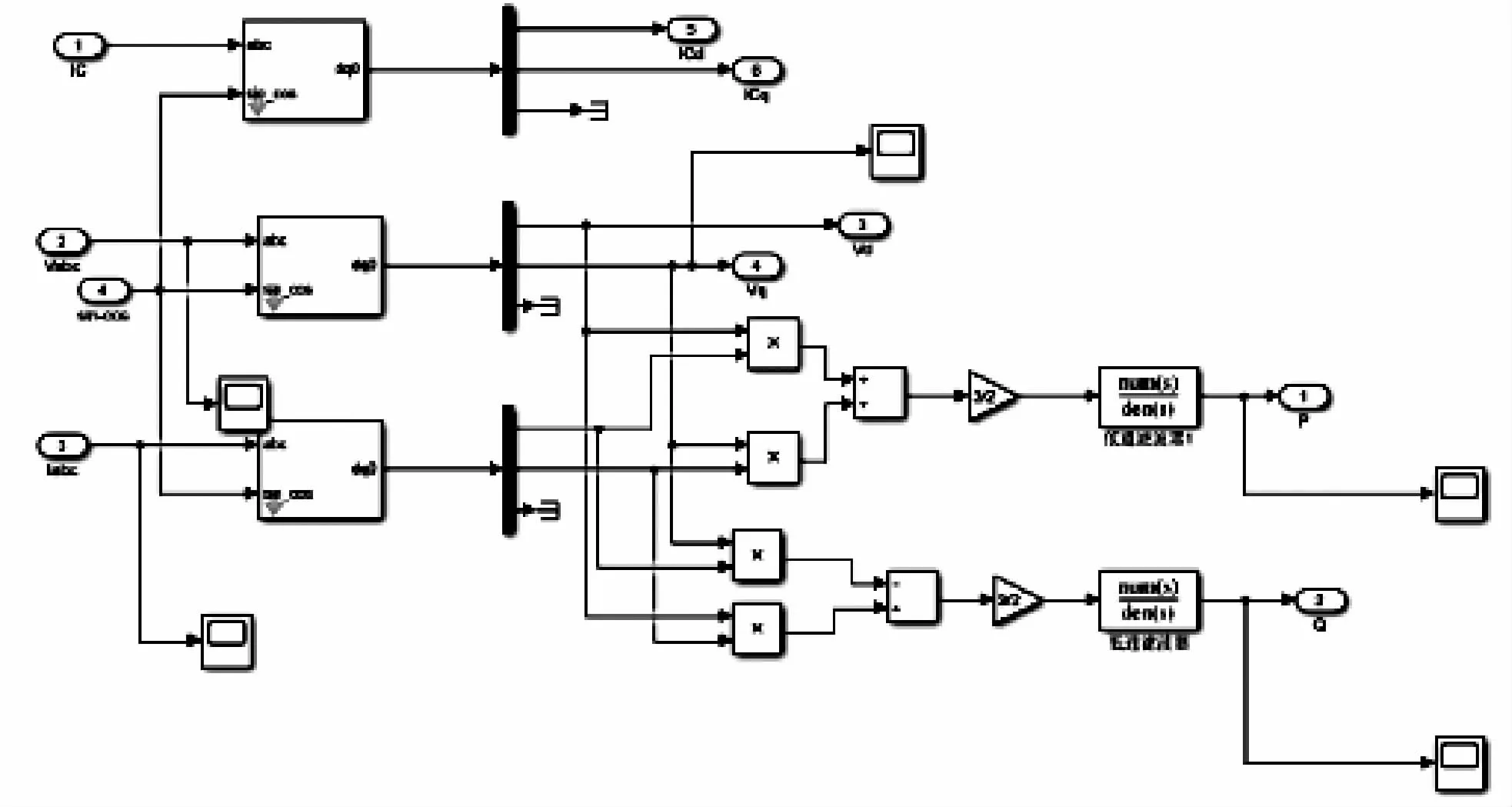
图8 dq变换和功率计算模块

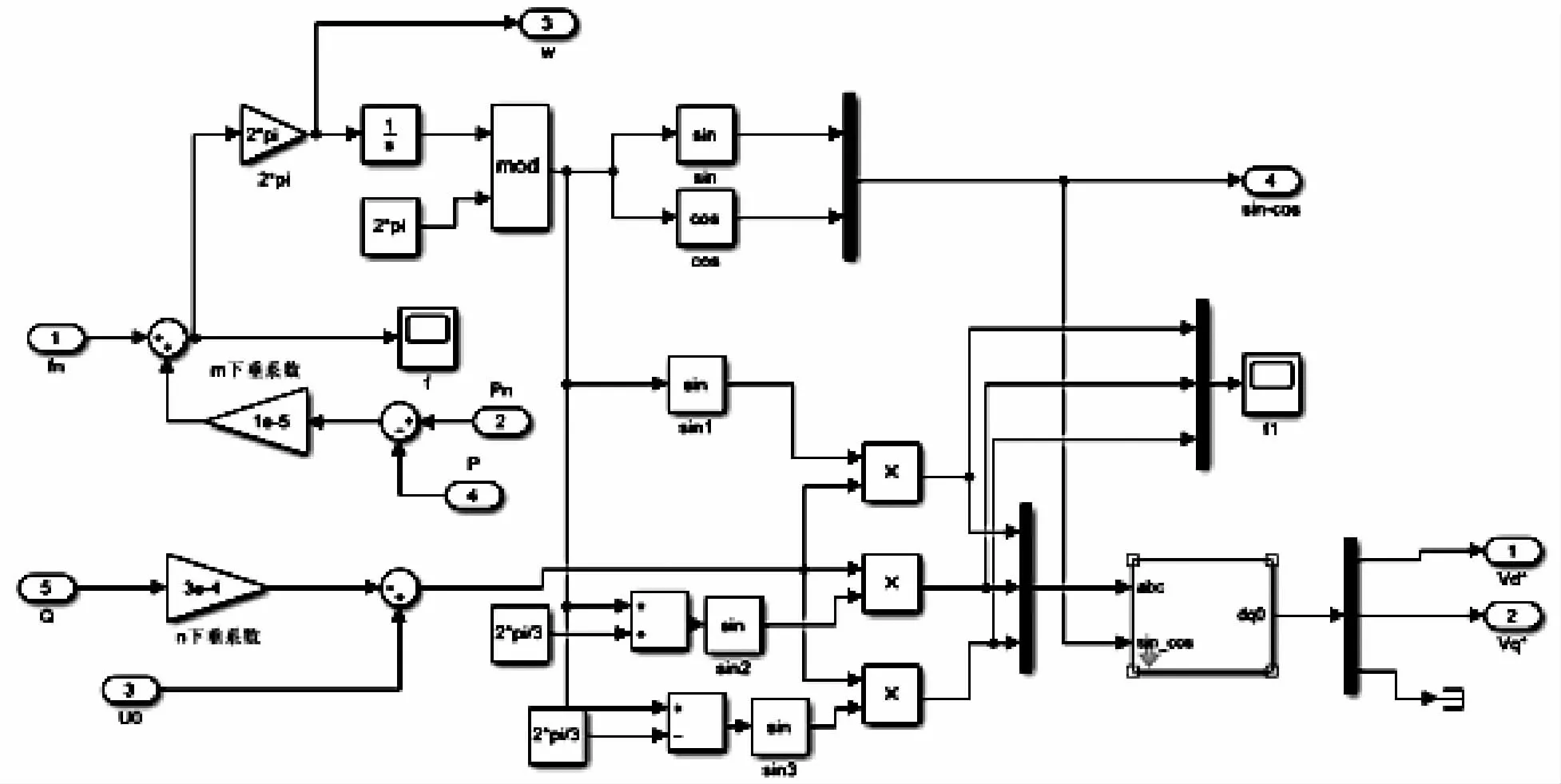
图9 下垂控制和电压合成模块

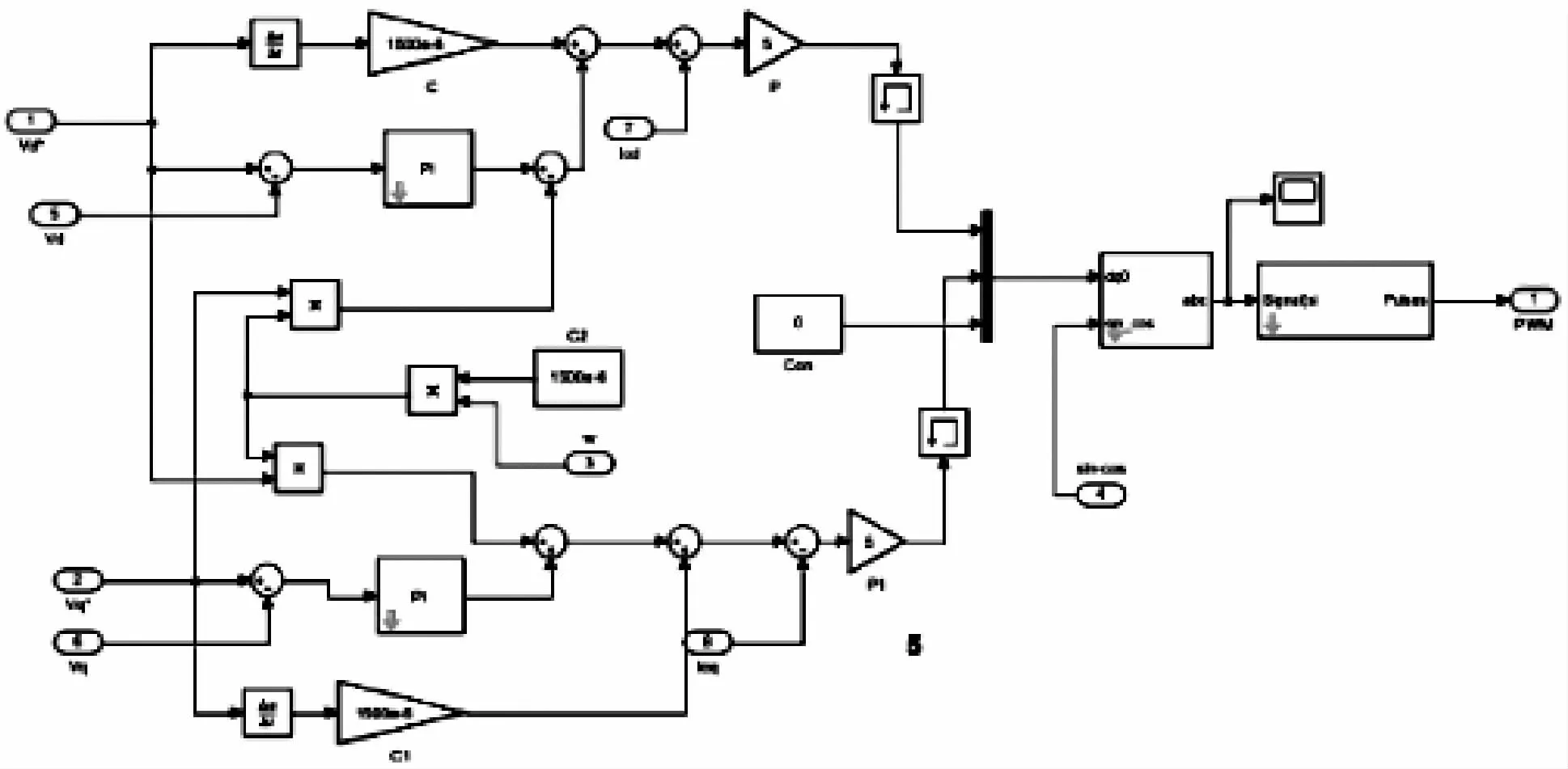
图10 电压电流双环控制

电压基于下垂控制方法的微电源孤岛模式仿真模型如图11 所示，主电路由直流电源、同步脉冲触发器、晶闸管整流桥、LC滤波器、负载等模块构成。
设置系统直流电源Udc＝800 V，额定频率fn＝50 Hz，U0＝311 V，Ps- f下垂系数m ＝1 × 10-5，Qs- U下垂系数n ＝3 × 10-4，额定有功功率Pn＝20 kW，负载1、电流双环控制部分如图10 所示，在该模块中可控的正弦调制信号~m从电流内环的输出经dq 反变换后得到，并输入到SPWM 模块与三角载波进行比较，然后得到6 路PWM控制信号。的参数P1＝20 kW，Q1＝10 kvar。负载2 的参数P2＝5 kW，Q2＝5 kvar。LC滤波的参数为：Lf＝0． 6 mH，Cf＝1． 5 mF，Rf＝0． 01 Ω，经过计算和调试，当电压、电流双环控制模块中的电压外环的PI调节的比例参数Kup和积分参数KuI分别取10 和100，能使负载电压零稳态误差，系统比较稳定；电流内环P 调节的比例参数K 为5，能使系统稳定并有较好的动态响应速度。

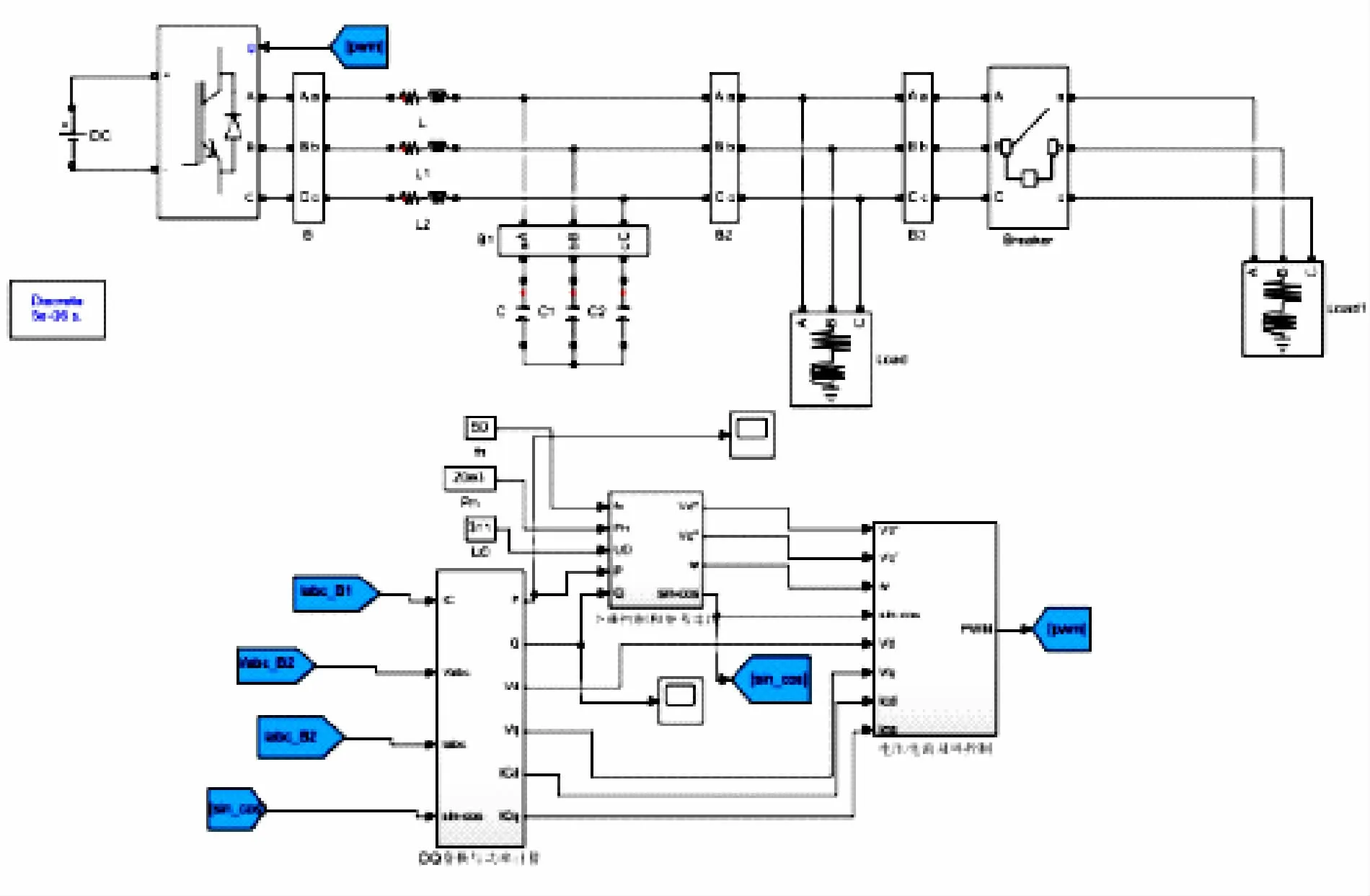
图11 系统仿真模型

4 仿真结果

为了验证根据下垂控制的微电网在孤岛模式下电压值和频率支撑，在负荷扰动的情况下电压值和频率会在合理的范围内波动［10］。设置仿真时间为1 s，在0． 4 ～0． 6 s 的时间内加入负荷2 。负荷扰动的情况下，观察负载端的电压、电流波形，微电源输出的有功功率、无功率波形，系统频率和微电源电压值的波形。仿真结果如图12 ～17 所示。

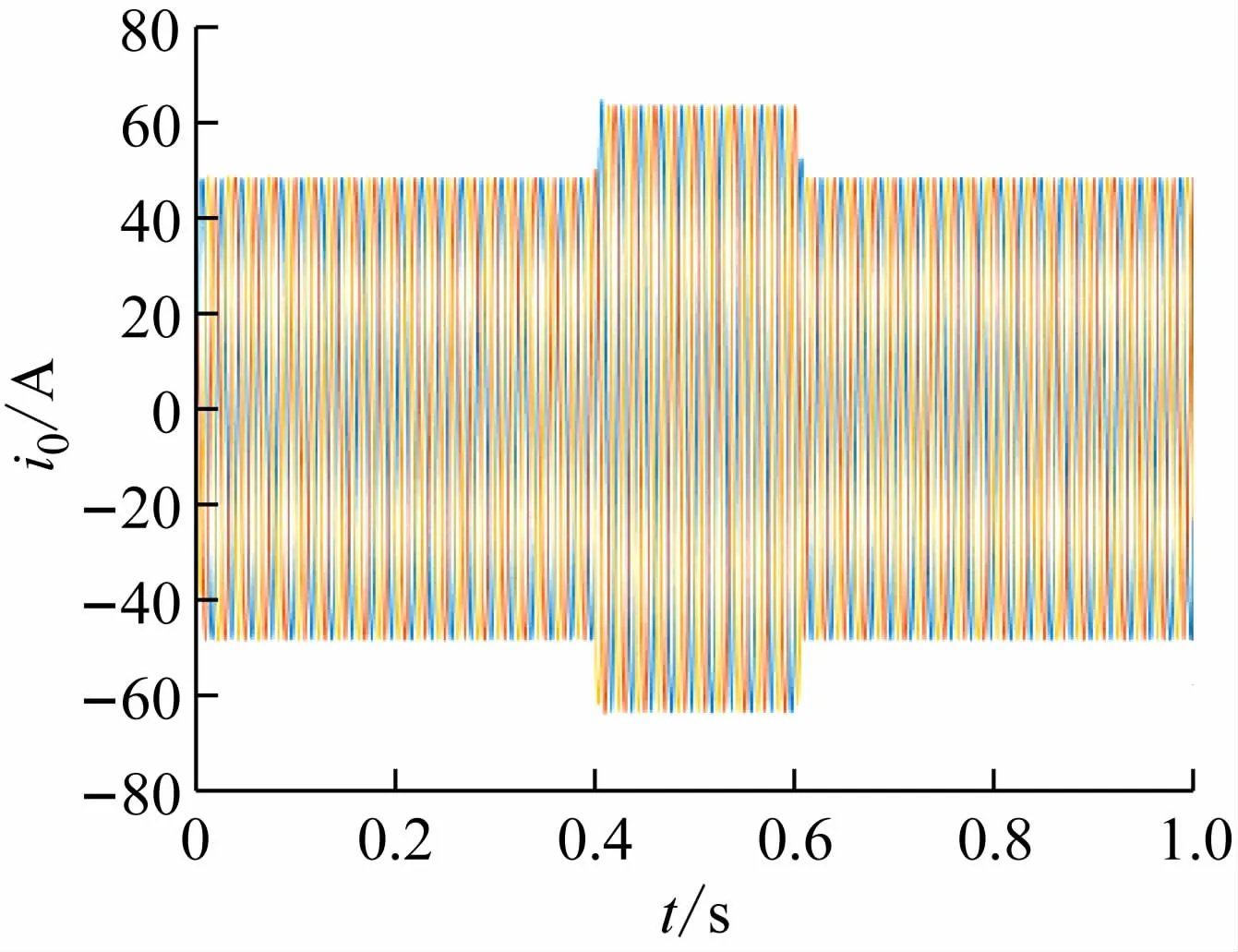
图12 负载端电流波形

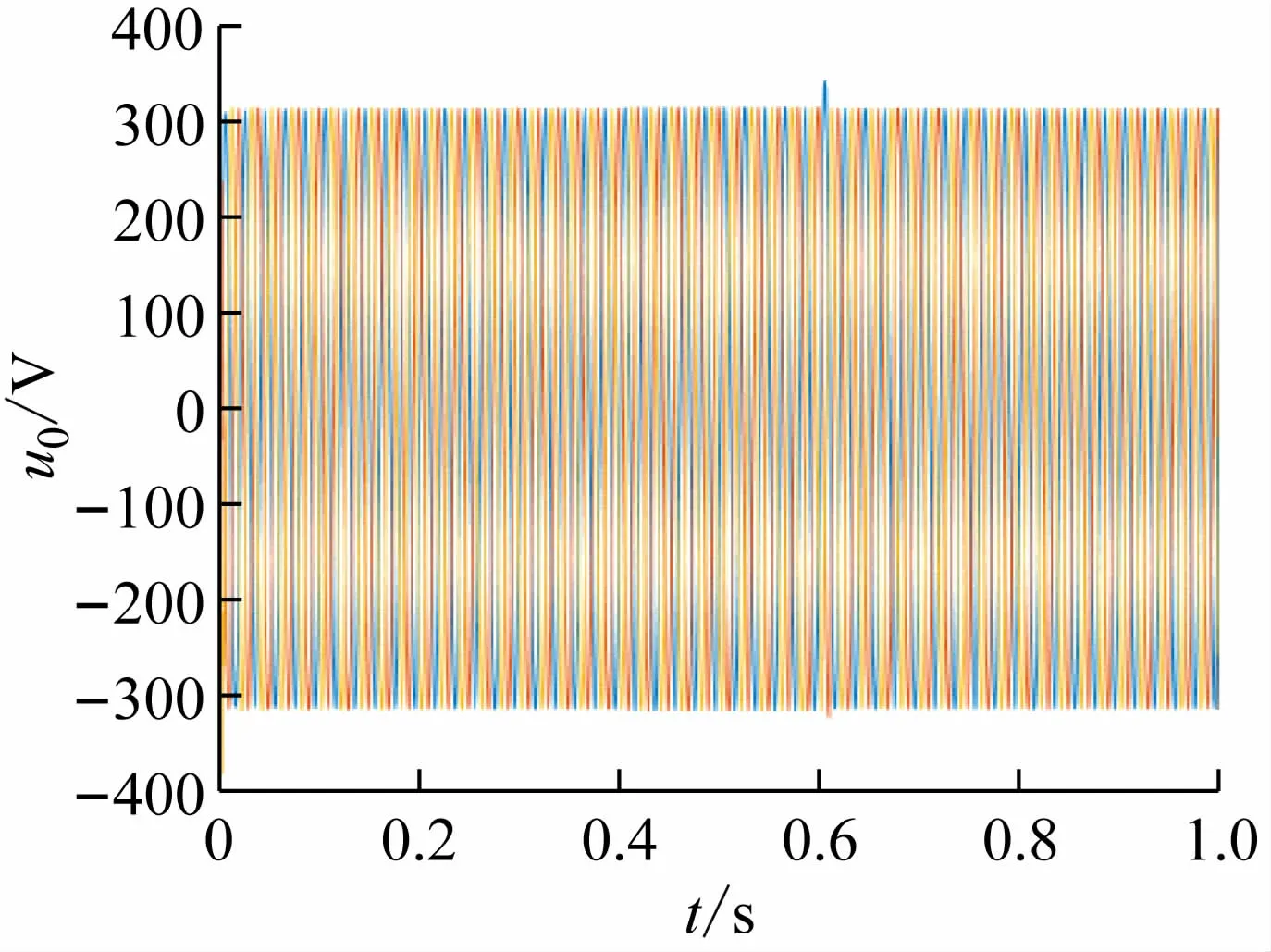
图13 负载端电压波形

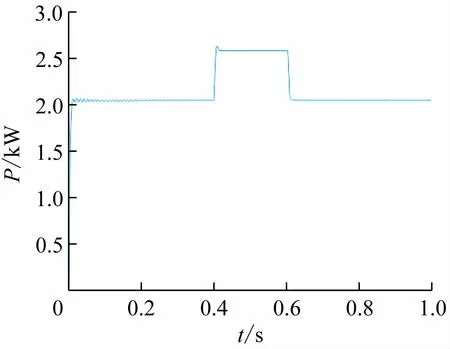
图14 微电源输出有功功率

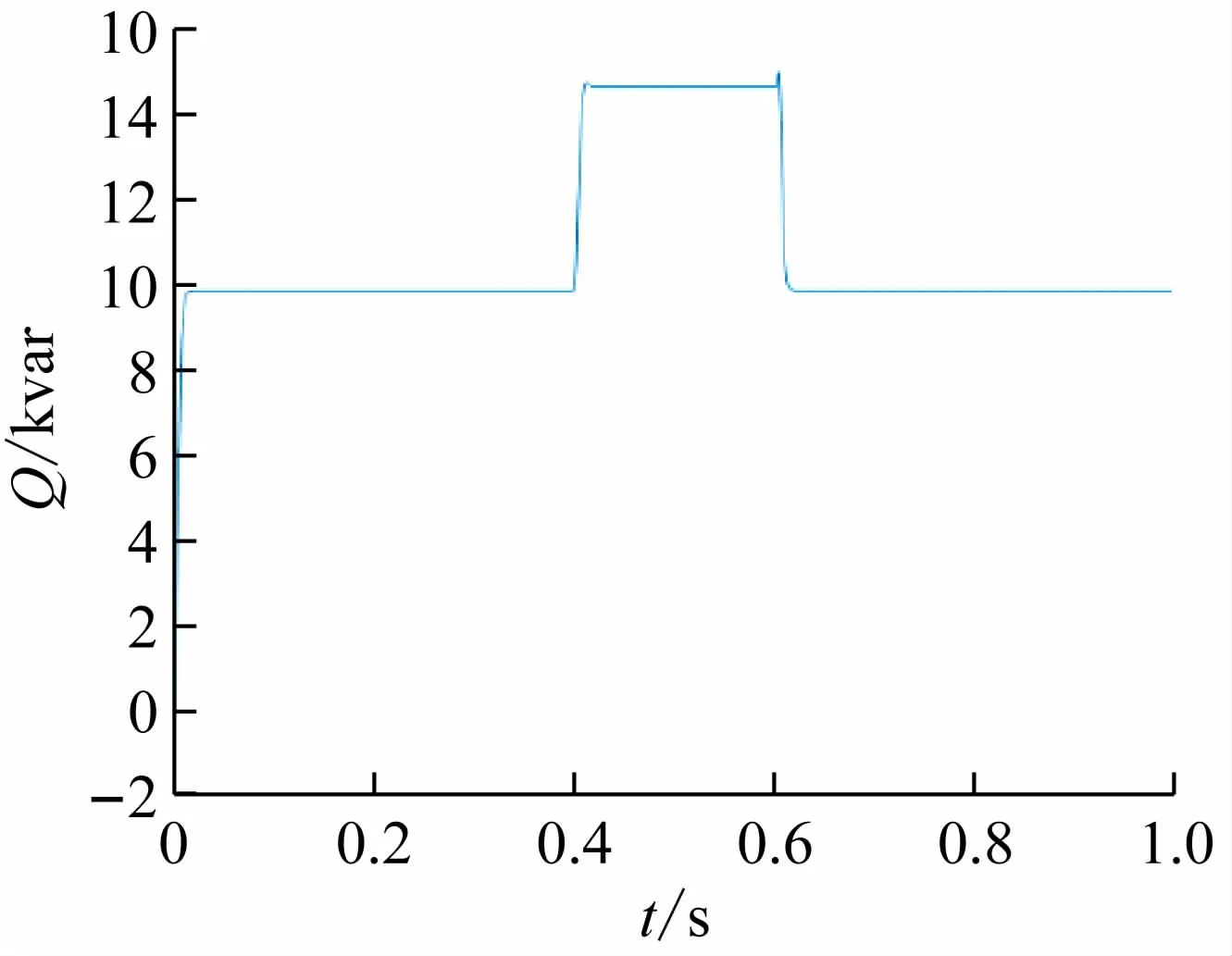
图15 微电源输出无功功率

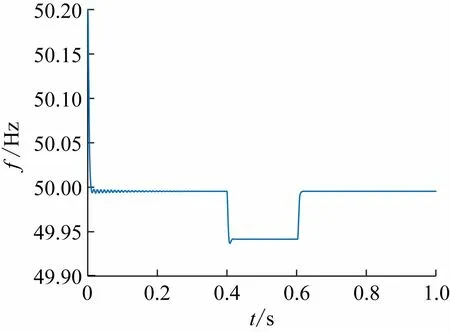
图16 系统频率

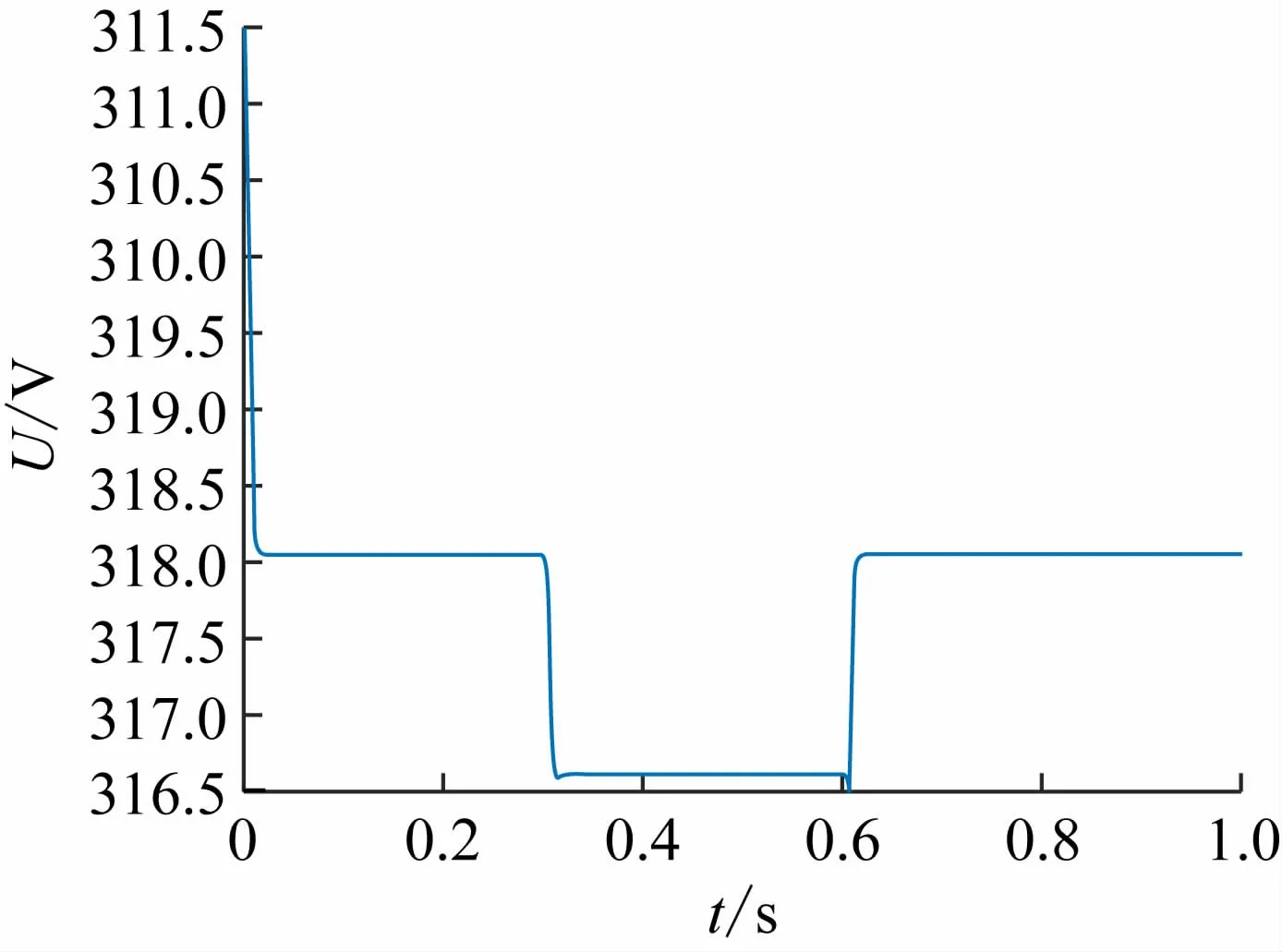
图17 微电源电压幅值

在0． 4 s负荷扰动时，从图12 负载端电流波形中可以得出系统相应速度快。从图13 负载端电压波形中可以得出负载端电压稳定，负载端电压零稳态误差。在0． 4 s时投入负荷2 时，对比图14 微电源输出有功功率和图16 微电网系统频率，当微电源发出的有功功率增长时，那么系统频率跌落；在0． 6 s 时切除负荷2时，微电源发出的有功功率减少，微电网系统频率增长，最终趋于稳定。对比图15 微电源发出无功功率和图17 微电源的电压幅值，在0． 4 s 时，微电源输出的无功功率增加，微电源电压幅值跌落；在0． 6 s 时，微电源输出的无功功率减少，微电源的电压幅值增加，最终趋于稳定。微电网系统频率变化范围不超过± 1%，微电源电压幅值变化范围不超过± 5%。