基于模糊C-均值聚类的缺失数据填充方法*

2020-09-14黄紫成

吉首大学学报（自然科学版） 2020年2期

黄紫成，李影

(仰恩大学工程技术学院，福建泉州 362014)

在加工、存储数据时常发生数据丢失，这对数据挖掘的有效性会造成一定的影响.对缺失数据的处理大概分为直接删除、填充或不处理.删除数据往往是删除缺失数据所在的样本，但如果删除的数据是至关重要的，那么对后续的操作会产生极大的影响.如果不处理缺失数据，因存在空值，对于有些算法就无法使用(如聚类算法).因此，有效的处理方式是对缺失数据进行填充[1-3].学者们对数据的填充提出了许多方法，如平均值填充、k近邻填充[4-6]、聚类填充[7-9]和粗糙集的不完备算法等.为了能得到更接近原始数据的完备数据集，笔者将使用模糊C-均值聚类算法进行数据填充，并与k近邻算法作比较.

1 k近邻填充算法

k近邻(k-Nearest Neighbor，KNN)填充算法是通过计算缺失数据样本与完整数据样本之间的欧式距离，选出距离最小的k个样本作为缺失样本的最近邻，再通过距离的反比加权平均而得到缺少数据的填充值[10-11].KNN填充算法步骤如下:

(ⅰ)初始化数据矩阵Xm×n，m为样本数量，n为属性维度；

(ⅲ)从完整样本中选出最小的k个距离作为缺失数据的k个近邻；

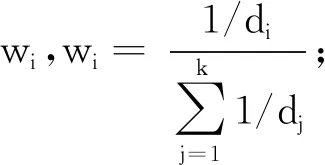
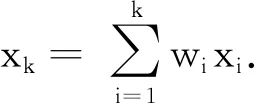
2 模糊C-均值聚类填充算法

模糊C-均值聚类(FuzzyC-Means，FCM)算法最早由E. Ruspini提出，后来J. C. Dunn和J. C. Bezdek将该算法从硬聚类算法推广为模糊聚类算法.模糊聚类算法是无监督的聚类算法，其聚类结果是每个数据样本点对聚类中心的隶属度[12-13].

对于数据集X={x1,x2,…,xn},cj(j=1,2,…,k)为k个类别的聚类中心，uj(xi)为第i个样本对应第j个类别的隶属度函数，则FCM算法的目标函数可以写成

(1)

这里隶属函数之和为1，b为加权指数，通常取为2.对(1)式求偏导，得到极小值时对应的必要条件为[12-13]

之后通过循环迭代就可计算出聚类中心和隶属度矩阵.FCM填充算法的流程如图1所示.得到隶属矩阵u之后，每个样本隶属于某个类别的概率已经确定.对于样本缺失的属性值，可通过计算每类对应属性的均值再乘以权重而得到.

图1 模糊C-均值聚类填充流程Fig. 1 Flow Chart of Fuzzy C-Means Clustering Filling

算法的时间复杂度主要为计算目标函数是否收敛于因子δ，若一直无法收敛，则可以控制循环迭代次数，如100次[14].

3 实验结果与讨论

本实验利用FCM和KNN算法完成填充，选用UCI数据库上的wine，wpbc，iono，ecoli等4组数据进行测试.为了比较填充前后数据与原始数据的差别，在4组数据上做随机缺失，缺失比例为5%，10%，15%，20%，25%.填充前后数据的均方根误差(Root Mean Squard Error，RMSE)计算公式为

实验平台为win10，CORE i7，内存8 G，MATLABR2017a.KNN填充算法中近邻k=3，FCM填充算法中聚类数目为6，收敛因子δ=10-6，实验数据见表1.

表1 数据集信息Table 1 Dataset Information

计算各数据集在FCM和KNN填充算法下的 RMSE，结果如图2～5所示.

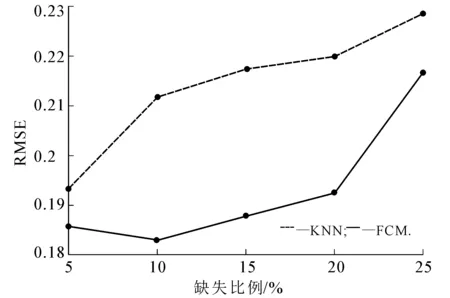
图2 wine数据Fig. 2 wine Data

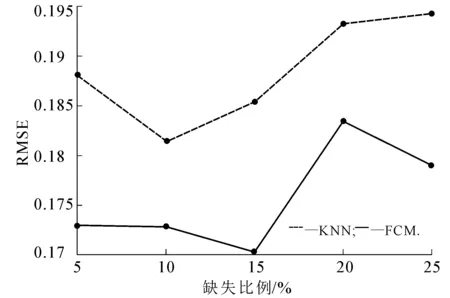
图3 wpbc数据Fig. 3 wpbc Data

图4 iono数据Fig. 4 iono Data

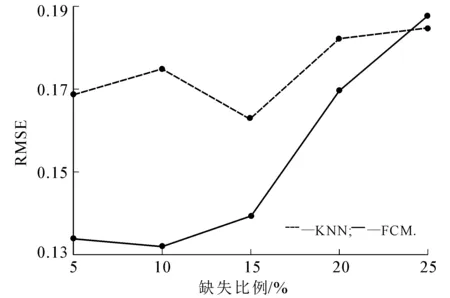
图5 ecoli数据Fig. 5 ecoli Data

由图2～5可以看出：在数据集wine，wpbc，iono中，FCM填充算法的RMSE都比KNN填充算法的小；在ecoli数据集中，缺失比例为5%，10%，15%，20%时FCM填充算法的RMSE较小，缺失比例为25%时KNN填充算法得到的RMSE较小，但二者较相近.缺失比例逐渐增加，RMSE也随之增大，但相对KNN填充算法，FCM填充算法总体保持在较小水平，这说明FCM填充算法在缺失值填充应用中能达到更好的效果.