Tempered分数阶微分方程解的全局存在性和稳定性*
2020-09-14张玉瑶钟文勇
张玉瑶,钟文勇
(吉首大学数学与统计学院,湖南 吉首 416000)
近年来,学者们对tempered分数阶微分方程理论和数值分析的研究非常活跃[1-6].例如,Zayernouri等[1]利用不动点定理探讨了tempered分数阶Sturm-Liouville特征值问题,Li等[2]和Morgado等[5]利用不动点定理讨论了一类Cauchy问题.但就tempered分数阶微分方程而言,局部Lipschitz条件下解的全局性质和稳定性问题还有待进一步研究.最近,对于连续和有界的分数阶积分函数,Tuan等[7]和Gomoyunov[8]都建立了涉及凸Lyapunov函数的不等式,并得到了一些含标准Caputo分数阶导数的微分方程解的稳定性判断依据.受文献[7-8]中的方法和结果的启发,笔者拟利用凸Lyapunov函数研究含Caputo型tempered分数阶微分方程初值问题解的全局存在性和稳定性.
1 相关定义
Caputo型tempered分数阶微分方程初值问题的具体形式如下:
(1)
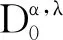
本研究中均假设0<α<1.
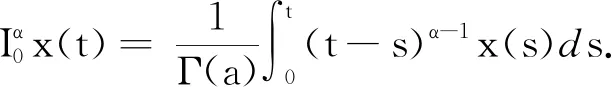


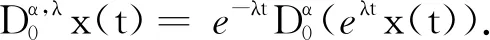
上述定义中的α为相应积分或导数的阶.
对于定义在[0,T]上、取值于Rd的矢量值函数,其相应的分数阶积分和导数也是Rd矢量值函数,它的分量由矢量值函数中相应分量的分数阶积分和导数构成.若矢量值函数的每个分量在此区间上都是非负的,则在区间上称之为非负函数.
2 相关引理

引理2[2]设f(·)∈C(Rd,Rd),b(·)∈C(R+,R)且在R+上有界.若f(·)在Rd上满足Lipschitz条件,则问题(1)在R+上存在唯一解.
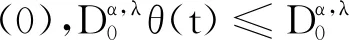
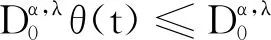
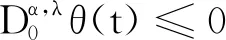
在建立主不等式之前,需要引入几个引理来描述Rd上凸函数的性质,并对凸函数做一些假设.由文献[10]中的定理4.5可直接得到如下结论:
引理4(链式法则) 设ν∈C1(O,R),则对于∀ϑ∈ACloc(I,O),ν(ϑ(·))∈ACloc(I,R),ν′(ϑ(t))=ν(ϑ(t))·ϑ′(t)在I中几乎处处成立,其中点·表示Rd上的内积.

引理5[11-12]设ν∈C1(S(ρ),R),则以下命题等价:
(S1)ν在S(ρ)上是凸的;
(S2)对于∀θ,ϑ∈S(ρ),有ν(ϑ)-ϑ(θ)-ν(θ)·(ϑ-θ)≥0;
(S3)ν的Hessian矩阵在S(ρ)中是半正定的.
令函数ν:S(ρ)|→R满足如下假设:
(H1)ν(ϑ)是S(ρ)上的凸函数且ν(0)=0;
(H2)ν(ϑ)在S(ρ)上是连续可微的;
(H3)对于∀ϑ∈S(ρ),有λ(ν(ϑ)-ν(ϑ)·ϑ)≤0.
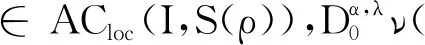
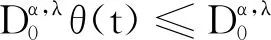
φα(t)=t-α,
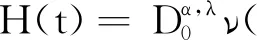
h(s)=(eλsν(ϑ(s)))′-ν(ϑ(t))·(eλsϑ(s))′,
其中0≤s (2) 以下待证对于∀t∈I有H(t)≤0.为此,先考察函数h(s),由链式法则可得 h(s)=(eλsφ(s))′+λeλs(ν(ϑ(t))-ν(ϑ(t)))·ϑ(t), (3) 其中φ(s)=ν(ϑ(s))-ν(ϑ(t))-ν(ϑ(t))·(ϑ(s)-ϑ(t)).由假设(H2)和中值定理可知,对于从ϑ(s)到ϑ(t)的线段上的某个点ξ,有φ(s)=(ν(ξ)-ν(ϑ(t))·(ϑ(s)-ϑ(t)).因此,对于I中几乎所有t,有 (4) 由假设(H3)和ν的凸性确保在区间[0,t]上φ≥0.结合(2)式可知,对于∀t∈I有H(t)≤0.证毕. 定义5如果对于∀ε>0,存在δ>0使得 |ϑ0|<δ成立,且问题(1)对应的解ϑ(t,ϑ0)满足不等式|ϑ(t,ϑ0)|<ε,t∈R+,那么称问题(1)中的零解是稳定的. 定义7[13]如果函数k在C(R+,R+)中是严格递增的且k(0)=0,那么称k在K中,记作k∈K. 现对问题(1)中的函数做进一步研究.令S(ρ)满足下列假设: (C1)f(·)∈C(Rd,Rd),且f(·)在S(ρ)上满足Lipschitz条件; (C3)S(ρ)是R+上的非负连续有界实值函数. 定理1假设S(ρ)满足(C1)和(C3).若存在函数k∈K和ν(ϑ)满足(H1)—(H3),且k(|ϑ|)≤ν(ϑ)和ν(ϑ)·f(ϑ)≤0在S(ρ)上成立,则对于每一个足够小的初值,问题(1)在R+上存在唯一有界解. 证明(C1)和Kirszbraun′s定理[14]确保存在函数g:Rd|→Rd,在R+上满足Lipschitz条件并与f具有相同的Lipschitz常数,且在S(ρ)上满足g=f.用函数g构造初值问题 (5) 于是由引理4可知,对于Rd上的任何初始数据ϑ0,问题(5)在ACloc(R+,Rd)中存在对应的唯一解. 接下来证明对于足够小的初始数据,问题(5)的对应解在R+上是有界的,且它也是问题(1)在R+上的唯一解.为此,在区间(0,ρ)中选择一个正数ρ0.函数ν(ϑ)的连续性和ν(0)=0的连续性能确保选取δ且0<δ<ρ0,只要ϑ在S(δ)中就有ν(ϑ) |ϑ(t,ϑ0)|<ρ0 (6) 在R+上成立. 现用反证法证明这个推断.若(6)式成立,则根据条件|ϑ(0,ϑ0)|=|θ0|<δ<ρ0和ϑ(t,ϑ0)的连续性可知,存在一个T1>0,使得对于∀t∈[0,T1],都有|ϑ(t,ϑ0)|<ρ0且|ϑ(T1,ϑ0)|=ρ0.在S(ρ)中,由k(|ϑ|)≤ν(ϑ)可得k(|ϑ(t,ϑ0)|)≤ν(ϑ(t,ϑ0)).再次利用(6)式和假设(H3)可知,在区间[0,T1)上,ν(ϑ(t,ϑ0))·g(ϑ(t,ϑ0))=ν(ϑ(t,ϑ0))·f(ϑ(t,ϑ0))≤0.结合假设(C3),(H1)—(H3)和引理6可知,对于∀t∈[0,T1],都有 再利用推论1,得到ν(ϑ(t,ϑ0))≤ν(ϑ0)e-λt.因此 k(|ϑ(t,ϑ0)|)≤ν(ϑ(t,ϑ0))≤ν(ϑ0)e-λt≤ν(ϑ0) 特别地,当t=T1时,有 k(ρ0)≤ν(ϑ(T1,ϑ0))≤ν(ϑ0)e-λT1≤ν(ϑ0) 这明显是矛盾的,所以(6)式在R+上成立,即解ϑ(t,ϑ0)在R+上有界.于是|ϑ(t,ϑ0)|<ρ在R+上显然成立,从而g(ϑ(t,ϑ0))=f(ϑ(t,ϑ0)),因此 这说明ϑ(t,ϑ0) 也是问题(1)在R+上的唯一解.证毕. 定理2定理1的假设中用(C2)代替(C1),其他假设不变.若λ>0, 则问题(1)的零解是渐近稳定的. 证明给出一个正数ε且ε<ρ.用ε代替定理1证明中的ρ0,则对于ε存在对应的δ(0<δ<ε),使得无论何时|ϑ0|<δ,问题(1)在R+上都存在唯一解 ϑ(t,ϑ0),且ϑ(t,ϑ0)在R+满足|ϑ(t,ϑ0)|<ε. 这验证了稳定性. 再次使用与定理1的证明相似的技巧,得到 k(|ϑ(t,ϑ0)|)≤ν(ϑ(t,x0))≤ν(ϑ0)e-λt. (7) 令t→+∞,由(7)式可推断出|φ(t,ϑ0)|→0.这确保了渐近性.证毕.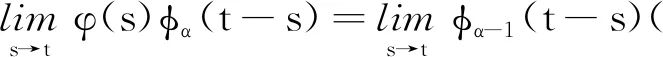
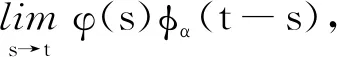
3 全局存在性和稳定性