两水平扩大设计基于中心化L2-偏差的均匀性*

李 洁，欧祖军

(吉首大学数学与统计学院，湖南 吉首 416000)

折叠反转是部分因子设计去除效应别名的一种重要方法.将通过折叠反转方案得到的跟随设计与初始设计合并得到的设计，称为扩大设计.折叠反转方案不同，会导致扩大设计的偏差值产生差异，所以要根据偏差值来筛选最优折叠反转方案.方开泰等[1]首次采用均匀性准则来评价最优折叠反转方案，并利用中心化L2-偏差来度量折叠反转方案的优劣.Li等[2]得到了两水平部分因子设计的所有最优折叠反转方案.雷轶菊等[3]得到了中心化L2-偏差下折叠反转设计的一些下界.随后，学者们[4-7]对偏差下界算法进行了优化和完善.胡柳平等[8]设计了一种计算偏差下界的新算法，相较于文献[3-7]中的下界算法，新算法更依赖于设计本身，得到的下界更优.基于该新算法，笔者拟研究两水平扩大设计基于中心化L2-偏差的均匀性.

1 基本概念

记有n个处理、k个因子的两水平部分因子设计为d，用+1和-1来代表两水平，+1代表高水平，-1代表低水平.当设计d中各因子的每个水平出现的次数相同时，称该设计为U-型设计[9].所有两水平U-型设计的集合记为U(n;2k).设计d对应一个n×k阶矩阵Xd=(xij)n×k=(x1,…,xk)，其中xi表示设计d的第i列，xij∈{+1，-1}.矩阵Xd的每一行对应设计d中的一个处理，每一列对应设计d中的一个试验因子.

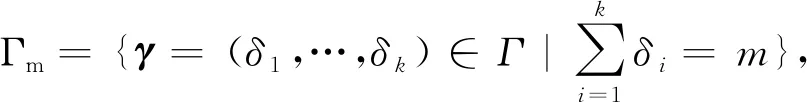
中心化L2-偏差可作为评判折叠反转设计方案优劣的标准.对于任意设计d∈U(n;2k)，CD(d)表示设计d的中心化L2-偏差值，其表达式为[11]

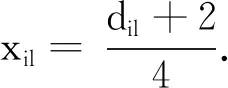
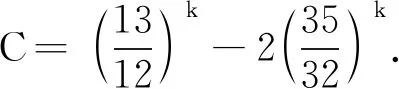
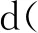
2 [CD(dγ))]2的新下界

对于任意设计d∈U(n;2k)和γ∈Γm,m=0,1,…,k,设计d的第i行和第j行的Hamming距离记为hij(d)，设计d的第i行和第j行相同元素的个数表示为cij(d)=k-hij(d).记N是由设计d中未反号的k-m列构成的子设计，同理可标记子设计N的第i行和第j行的Hamming距离hij(N)和相同元素的个数cij(N)=k-m-hij(N).对于任意两水平设计d∈U(n;2k)和γ∈Γm，有

(1)

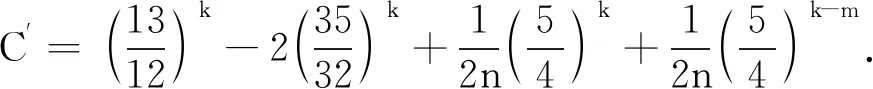
对于设计d∈U(n;2k)和γ∈Γm，笔者基于引理1给出了扩大设计d(γ)的中心化L2-偏差CD(d(γ))的一个新下界：

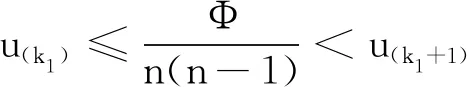
证明由(1)式可知，

证毕.

对于设计d∈U(n;2k)和γ∈Γm，有如下相关的下界结论：

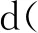
这里：

(2)

根据定理1和引理2给出的下界值进行择优选取，可以得到如下结论：

考虑到设计d中任意2个不同行i,j(i≠j;i,j=1,…,n)的Hamming距离hij(d)为常数λ时，表达式有一定的简化，于是得到如下结论：

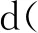
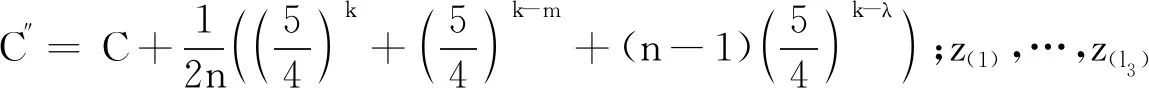
证明

证毕.

同样地，对于设计d的任意2个不同行i,j(i≠j;i,j=1,…,n)之间的Hamming距离hij(d)是常数λ的情况，有如下下界算法：

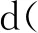
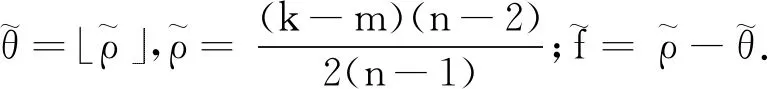
针对设计d的任意2个不同行i,j(i≠j;i,j=1,…,n)之间的Hamming距离hij(d)是常数λ的情况，根据定理3和引理3给出的下界值进行择优选取，可以得到如下结论：

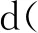
3 数值实例

例1考虑设计d∈U(8;214)，它可以表示为如下矩阵形式：

表1给出了设计d的具体数值计算结果.

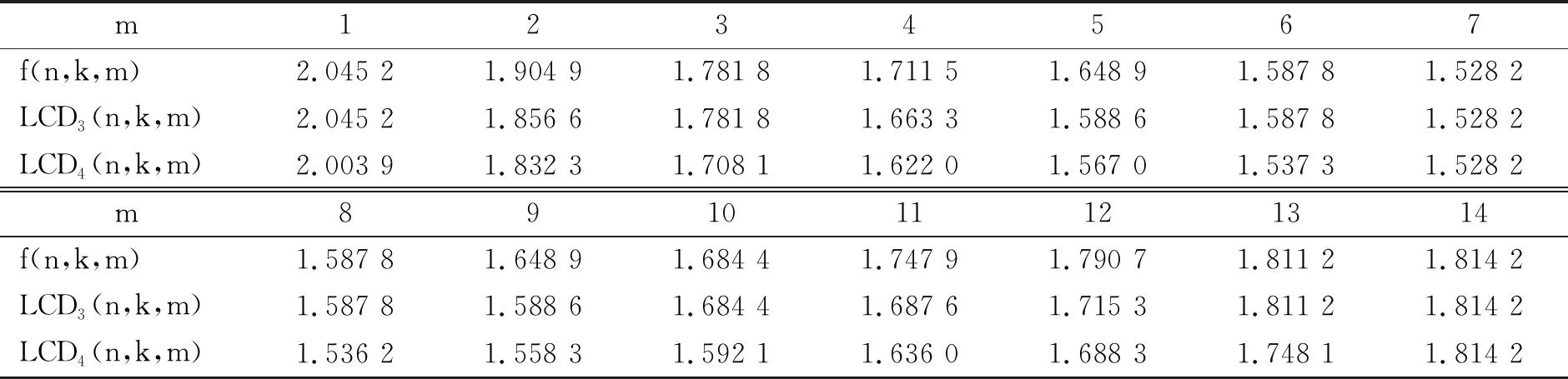
表1 设计d的数值结果Table 1 Numerical Results of d

从表1可知，当1≤m≤14时，定理3中的下界LCD3(n,k,m)都比原有下界LCD4(n,k,m)更好，且大部分下界是达到偏差下界的.

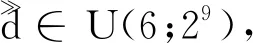
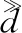
表2 设计的数值结果Table 2 Numerical Results of

表2(续)Table 2 (Conituned)

从表2可知，当m=5和m=6时，定理1中的下界LCD1(n,k,m)比原有下界LCD2(n,k,m)更好，且当m=9时，下界LCD1(n,k,m)是达到偏差下界的.