Mathematica 数学软件与函数极限和导数教学

王景艳 李凯敏

（保山学院数学学院 云南·保山 678000）

本文主要借助高等数学教材，讨论Mathematica数学软件辅助高等数学函数极限和导数教学的研究，主要研究一元和二元函数的极限及一元函数的导数和二元函数的偏导数，通过Mathematica数学软件的简单实例教学，提高教学效率和学生学习高等数学的积极性。

1 一元函数极限的实例教学

极限在高等数学中占非常重要的位置，是高等数学的理论基础，高等数学里的很多内容都和极限有关，比如说连续、导数和定积分，所以学生们学好函数极限是非常重要的。因此，借助Mathematica 数学软件的符号计算功能，让学生很好的理解和掌握极限，为后续课程内容打下基础。

解：分别求它们的数值解，因为它们都是偶函数，所以 的值只取正的，输入输出分别如下：

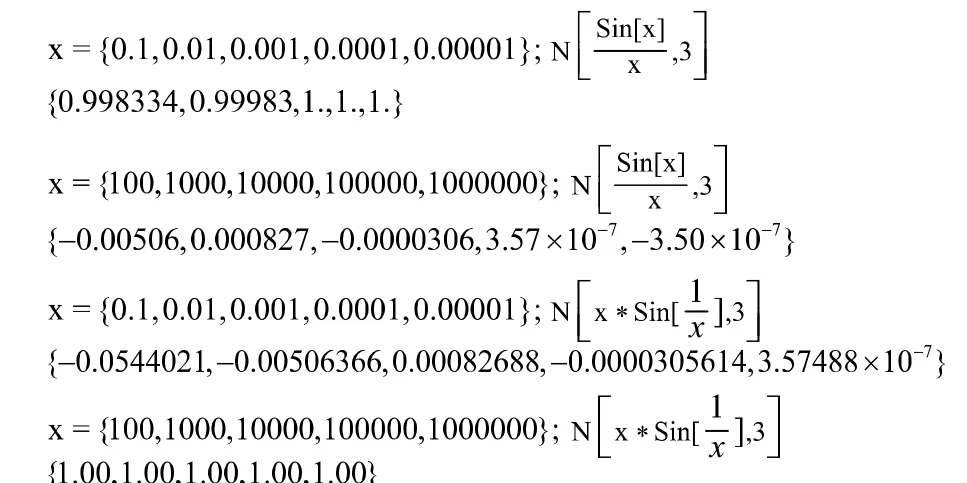
输出：如图1 所示。

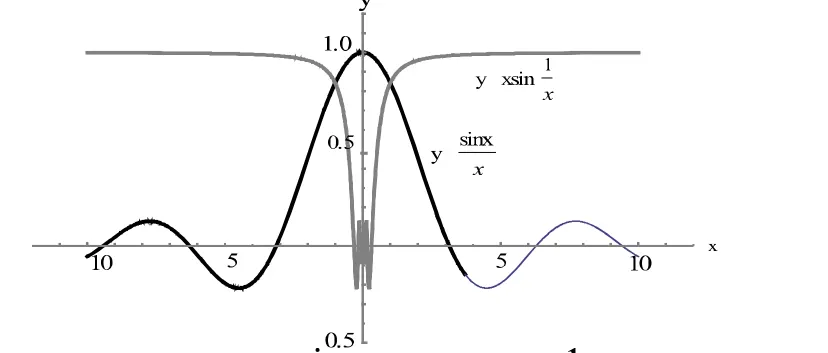
图1 函数的图形

2 二元函数极限的实例教学

二元函数与一元函数的极限定义和求解是相似的，但二元函数的极限比一元函数的极限要复杂些。

3 一元函数导数及其应用的实例教学

导数是高等数学中重要的基础概念，在高等数学中占有重要位置。学生们往往记不住导数公式，或是在求导过程中不注重方法。

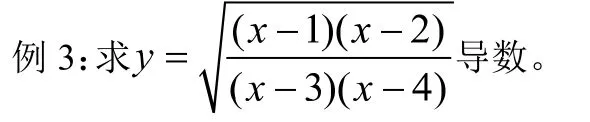
分析：这个题如果不注重求导的方法和化简，那么过程繁琐，计算量大，但学生往往忘记了对数求导法，直接求解，但不知道结果是否正确。那么通过 Mathematica 数学软件的多项式运算，对其化简，分项，通分，输入输出：

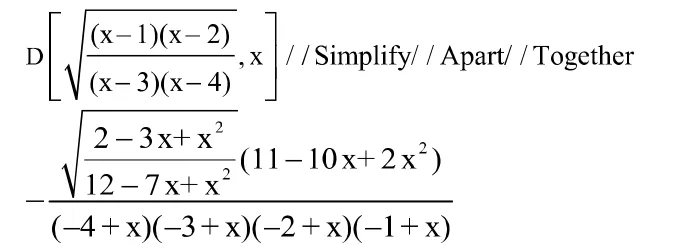
但这个题最简单的方法是对数求导法，但结果形式上不一样，那么是不是对的呢？可以进行验证，把对数求导法的结果进行通分，故输入输出：

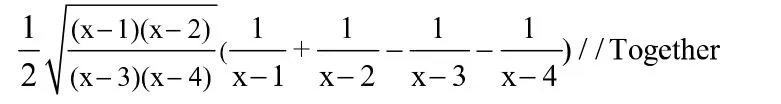
4 二元函数偏导数及其应用的实例教学

二元函数的偏导数往往比一元函数的导数复杂，因为它有两个自变量，学生在学习和求解中出现畏难情绪，有时求解出来了，但不知道对不对，还有些函数看似简单，但求解复杂，因此借助Mathematica 数学软件的符号计算功能，可以求解，并进行验证。

分析：先求一阶偏导，再求二阶偏导，Mathematica 数学软件求偏导数的命令和一元函数的类似，输入输出，有

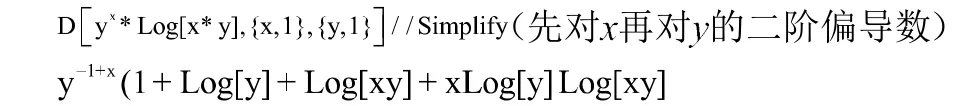
还可以演示求解更高阶导数的偏导数，来激发学生的学习积极性。

5 结论

本文主要探讨了 Mathematica 数学软件辅助一元和二元函数的极限及一元函数的导数和二元函数的偏导数及其应用的几个典型实例。那么在实际教学中，还可以不断的研究和改进命令，不断的实验，不仅帮助学生掌握知识和发现规律，提高教学效率，还可以提高学生学习高等数学的积极性，培养他们自主学习的良好习惯。