引导学生利用Matlab 处理大学物理实验数据的探究

曹跃龙 贾婉丽 张 琳

（西安理工大学理学院 陕西·西安 710048）

0 引言

学生完成物理实验数据测量后，课后的实验数据处理是一个重要环节，利用传统的数据处理方法处理数据，学生往往需要花很长时间完成，传统的数据处理方法计算繁琐、容易出错。如今，运用计算机应用软件进行实验数据处理已经成为一种趋势。Matlab、Mathematica、Maple 等计算机数学语言具有强大的计算功能和绘图功能，在物理实验中应用这些软件进行数值模拟实验和复杂数据处理非常方便。但是大学物理实验在本科一年级学生中开设，大部分学生并不具备编程基础，如何引导学生使用这些软件完成数据处理就需要我们任课老师潜心研究了。Matlab 相比于高级计算机C 语言而言，简单易学，上手快，掌握一些简单的函数完全可以进行实验数据处理。

1 实验绪论课讲授简单matlab 函数的必要性

大学物理实验都是从绪论课开始的，即介绍大学物理实验的目的、实验内容、实验方法，其中一个重要的内容介绍是如何处理实验数据，常规的实验数据处理不外乎：列表法、逐差法、作图法、最小二乘法。这几种方法都有各自的优点，但也都存在缺点。列表法简单明了，形式紧凑，各数据间易于参考比较，但也存在不能直观地显示数据变化趋势的缺点。作图法能将物理量间的对应关系、变化趋势以及数据的极值点、转折点、周期性等以最直观的方式显示出来，但也存在主观随意性大不可避免地引入一些附加误差。逐差法的优点是计算简单，可以最大限度的利用测量数据，但要求函数必须满足一元函数，且自变量必须是等间距变化，函数间不是线性关系的需要转换成线性关系，这样的处理都引入了误差的存在。最小二乘法可以精确地拟合出曲线的参数，但存在计算量过大，学生手工计算难度太大，所以借助于计算机高级语言完成实验数据处理是很有必要的。

绪论课中可适当引入matlab 的简单计算函数，鼓励学生主要通过自学应用matlab 处理实验数据中的列表法、画图法、逐差法以及最小二乘法的繁复计算，使学生学以致用。

2 几种常用实验数据处理方法例子

2.1 单变量的统计计算

利用标准偏差表示测量结果时，对于多次测量的样本标准偏差用 表示

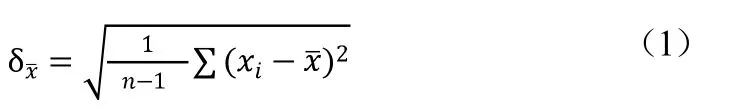
平均标准偏差用

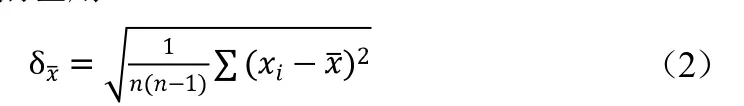
可用的简单函数有：mean（）（求平均值）、var（）（求样本方差）、std（）（求样本标准差）

例如：测量某长度所得数据如下（单位mm）：

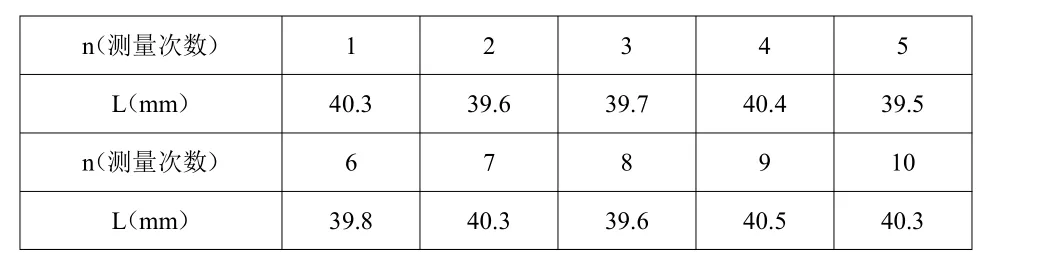
n（测量次数） 1 2 3 4 5 L（mm） 40.3 39.6 39.7 40.4 39.5 n（测量次数） 6 7 8 9 10 L（mm） 39.8 40.3 39.6 40.5 40.3

试将测量结果按照规范式正确表述。

解：matlab 程序如下：

clear all

L=[40.3 39.6 39.7 40.4 39.5 39.8 40.3 39.6 40.5 40.3]；

L1=mean(L) %求解平均值

a1=std(L) %求解样本标准偏差

a2=a1/sqrt(10) %求解平均标准偏差

运行结果：L1=40.0000mm；

a1=0.3916mm；a2=0.1238mm

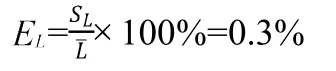
2.2 逐差法

用逐差法计算数据，要求原始数据必须是偶数个，必须使用隔n 项逐差，并求对应项的逐差，其算术平均值为：

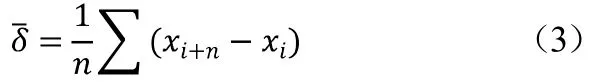
算术平均值绝对误差为：

相对误差为：

例如：一竖直轻弹簧的长度L和下端所加负载质量的关系如下：

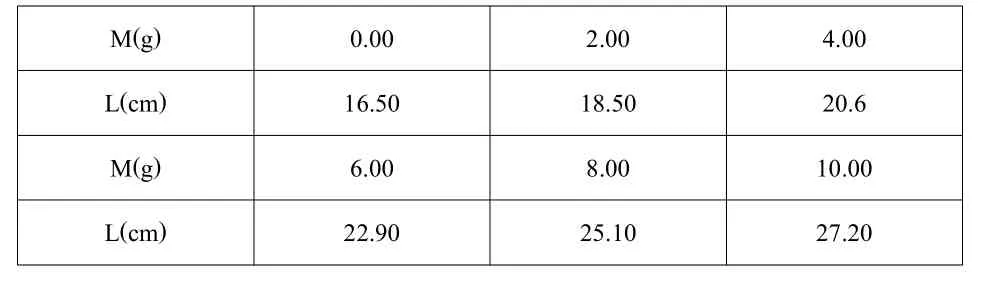
M(g) 0.00 2.00 4.00 L(cm) 16.50 18.50 20.6 M(g) 6.00 8.00 10.00 L(cm) 22.90 25.10 27.20

试用逐差法处理数据，求出伸长量的算术平均值、绝对误差和相对误差以及弹簧的倔强系数 。

clear all

g=9.8；

m=[0.00 2.00 4.00 6.00 8.00 10.00]；

L=[16.50 18.50 20.6 22.90 25.10 27.20]；

delL1=(L(6)-L(3))*10e-2；

delL2=(L(5)-L(2))*10e-2；

delL3=(L(4)-L(1))*10e-2；

delL=1/3*(delL1+delL2+delL3)； %算术平均值

delm=(m(6)-m(3))*10e-3；

k=delm*g/(delL) %弹簧的倔强系数

deldelL=1/3*(delL1-delL+delL2-delL+delL3-delL) %算术平均值绝对误差

E=deldelL/dell %相对误差

运行结果：弹簧倔强系数k = 0.9000；算术平均值 6.533；算术平均值绝对误差 2.961 -15%；相对误差=4.5 -15%。

2.3 一元线性回归分析

其中a，b 是需估计的两个参数。现有x 和y 的n 组测量值(，可根据最小二乘法估计 a，b 的值。

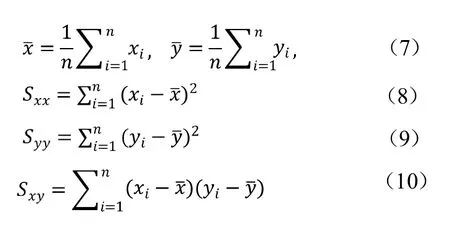
所以得到：

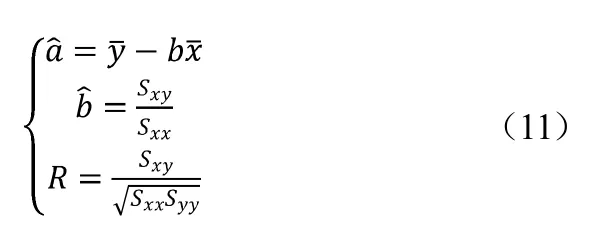
R 为线性相关系数。

平均标准偏差为：

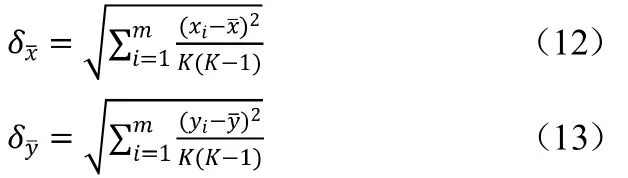
其中K 是参数的数目。

例如：一物体作匀速直线运动，在不同时刻t，观察运动距离S，结果如下：

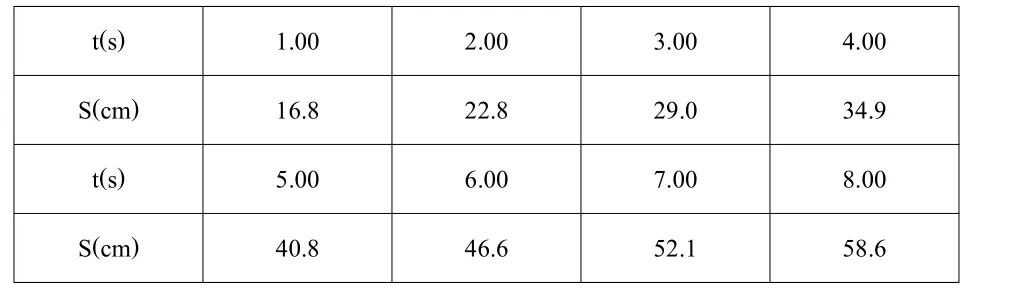
t(s) 1.00 2.00 3.00 4.00 S(cm) 16.8 22.8 29.0 34.9 t(s) 5.00 6.00 7.00 8.00 S(cm) 40.8 46.6 52.1 58.6

试用最小二乘法求出物体运动速度。

clear all

t=[1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00]；

S=[16.8 22.8 29.0 34.9 40.8 46.6 52.4 58.6]；

a=polyfit(t,S,1)%a(1)为 b，a(2)为 a

t1=1：8；k=2；

S1=a(1)*t1+a(2)；

Sn=a(1)*t+a(2)；tn=(S-a(2))/a(1)；

sigmaSn=sqrt((Sn-S)*(Sn-S)'/(k*(k-1))),%S 平均标准偏差

图1 物体运动距离S 与时间t 的最小二乘法拟合

sigmatn=sqrt((tn-t)*(tn-t)'/(k*(k-1))),%t 的平均标准偏差

tp=mean(t),Sp=mean(S),%平均值

Ltt=(t-tp)*(t-tp)',

Lss=(S-Sp)*(S-Sp)',

Lts=(t-tp)*(S-Sp)',

r=Lts/sqrt(Ltt*Lss),%线性相关系数

运行结果：a=5.9440 10.9893；sigmaSn=0.0025；sigmatn=0.0424；tp=4.5000；Sp=0.3774；r=1.0000

所以速度v=5.944m/s，物体运动的距离S 与时间t 的关系为：s=5.94t+10.99，时间 t 的平均值：t=4.50(s)，物体运动距离的平均值：=0.3774(m)，时间t 的平均标准偏差为： =0.0424，物理运动距离的平均标准偏差为： =0.0025，线性相关系数为：=1，相关度非常好。

3 小结

通过以上几种数据处理常用方法的例子可以看出，Matlab功能强大,在物理实验数据处理中使用非常方便。引入一定的机制鼓励学生积极自学并使用Matlab 语言来处理大学物理实验数据，不仅提高了他们自身的素质，而且能够提高学生学习兴趣。