灰色综合评价模型在建筑项目评标中的应用

张海涛 孙峙华

(江汉大学机电与建筑工程学院，湖北 武汉 430056)

灰色综合评价模型是利用灰色关联度作为测度，来比较各备选方案的优劣程度。该模型具有分析思路清楚、计算方法简单、可以充分利用已白化的信息、综合评价误差小等特点[1]。本文以工程技术人员普遍掌握的Excel电子表格为计算工具，研究如何在建筑工程项目评标工作中应用灰色综合评价模型。

1 灰色综合评价的数学模型

灰色综合评价可分为单层次综合评价和多层次综合评价，后者与前者在评价方法上相似，并且是在前者的计算基础上进行评价的。这里只具体论述单层次的评价模型。

1.1 确定评价指标及最优指标集

评价指标是评价对象的各类属性或性能，在建筑工程项目中常见的有技术指标、经济指标、质量指标、环境指标、社会指标、风险指标等。最优指标是从各评价对象的同一指标中选取最优的一个，而由这些最优的指标组成的集合即最优指标集。评价对象的评价指标和最优指标集可形成一个初始决策矩阵U：

(1)

1.2 初始决策矩阵的规范化处理

由于各评价指标的量纲不尽相同，因此为了能够相互比较，需要进行指标的规范化处理，常用的方法有数值均值化和初值化。对式(1)的初始决策矩阵进行均值化或初值化后可得到一个规范化的决策矩阵V:

(2)

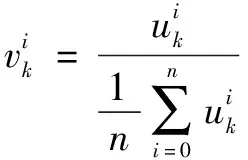
1.3 计算灰色关联系数，确定判断矩阵

(3)

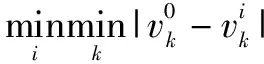
由式(3)得到的灰色关联系数确定判断矩阵R：

(4)

1.4 灰色综合评价

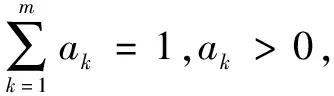
B=RAT

(5)

其中，B=(b1,b2,…，bn)T中的bi为评价对象i与理想方案(其评价指标为最优指标)的关联程度，bi越大表示评价对象i越接近理想方案，因此可以根据bi的大小得到各评价对象的优劣顺序。

2 基于Excel的灰色综合评价应用

Excel是一个面向经验管理者的数据分析软件，目前已成为企事业单位日常业务管理和经营决策的必备工具，灰色综合评价模型应用在Excel中能够使复杂的数学计算问题简单化，并且易于工程技术人员掌握。下面以文献[1]中的一个招投标案例说明基于Excel的灰色综合评价模型的应用，案例的技术经济及其他评标数据如表1所示，经过专家评定，七项评标指标的权系数为A=(0.35，0.15，0.1，0.1，0.1，0.15，0.05)，要求从参与投标的A,B,C三家建筑施工企业中选择中标单位。

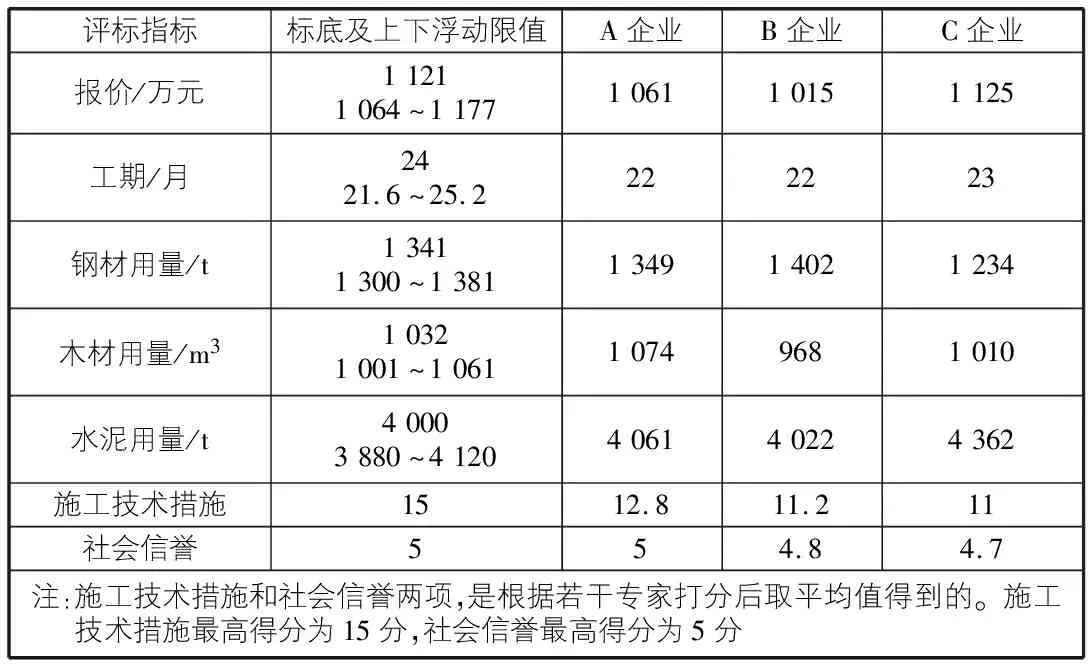
表1 标底与投标企业指标表

以标底中的最优值组成最优指标集，若无标底也可采用各投标人的合理评标指标最优值等方法组成最优指标集，以最优指标集组成评价指标的方案为理想方案。本案例在Excel中的计算步骤如下：

步骤1：按表1数据在Excel中输入初始数据图1单元格B3:H6所示，并用AVERAGE函数计算各项指标的平均值如单元格B7:H7所示。

步骤2：对单元格B3:H6中的数据进行规范化处理。以指标值初始值除以平均值得到均值化结果，具体操作可在单元格B9:B12中分别按“=B3/B7”“=B4/B7”“=B5/B7”“=B6/B7”计算后再分别点击上述四个单元格横向拖动鼠标至H9:H12实现其他单元格的自动计算，计算结果如单元格B9:H12所示。

步骤3：进行两极差计算,在单元格B14,B15,B16中分别按“=ABS(B9-B10)”“=ABS(B9-B11)”“=ABS(B9-B12)”计算后，同步骤2的方法，可自动计算出其余极差如单元格B14:H16所示，可知两极最小差为0，两极最大差为0.32。

步骤4：按式(3)计算灰色关联系数，形成判断矩阵。在计算单元格B18:B20后可前述方法实现自动计算，如对单元格B18按“=0.5×0.32/(ABS(B9-B10)+0.5×0.32)”计算。计算结果如单元格B18:H20所示。

步骤5：输入指标权重如单元格B22:H22，按式(5)计算灰色评价权向量。选取单元格E24:E26，在编辑栏中键入“=MMULT(B18:H20,TRANSPOSE(B22:H22))”，按“ctrl+shift+enter”组合键后计算得到灰色评价权向量如单元格E24:E26所示。按前述评价对象优劣判断标准可知，A企业应该为中标单位。

3 结语

针对建筑工程项目评标，基于灰色关联分析的灰色综合评价模型有较好的适用性，如本文案例的结论，采用灰色综合评价克服了一般评标方法中普遍存在的以商务标优势压倒技术标优势而获得中标的现象，并且利用Excel数据处理功能能够简单地完成评价模型的建立、运算，从而使评价工作易于掌握，工作效率得以提高。

灰色综合评价模型具有良好层次的拓展性，当评价问题的评价指标众多而需要对指标进行分层次处理时，以第一层次的评价结果B=(b1,b2,…,bn)T组成第二层次的评价矩阵后，按本文中建立的单层次的评价模型同样可以进行第二层次的评价，类似地也可以进行更高层次的评价。