BICYCLIC GRAPHS WITH UNICYCLIC OR BICYCLIC INVERSES∗†

Xia Wang,Hong Bian

(School of Mathematical Sciences,Xinjiang Normal University,Urumqi 830054,Xinjiang,PR China)

Haizheng Yu

(College of Mathematics and System Sciences,Xinjiang University,Urumqi 830046,Xinjiang,PR China)

Abstract

Keywords inverse graph;unicyclic graph;bicyclic graph;perfect matching

1 Introduction

LetGbe a simple,undirected graph onnvertices.We denote its vertex set byV(G)and its edge set byE(G).We usePnto denote the path onnvertices.And we use[i,j]to denote an edge between the verticesiandj.The adjacency matrixA(G)ofGis a square symmetric matrix of sizenwhose(i,j)th entryaijis 1 if[i,j]∈E(G)and 0 otherwise.

A graphGis nonsingular if its adjacency matrixA(G)is nonsingular.LetGbe an unweighted graph andGWbe the positive weighted graph obtained fromGby giving weights to its edges using the positive weight functionW:E(G)→(0,∞).The unweighted graphGmay be viewed as a weighted graph where each edge has weight 1.A perfect matching in a graphGis a collection of vertex disjoint edges that covers every vertex.If a graphGhas a unique perfect matching,then we denote it byM.In addition,whenuis a vertex,we shall always useu′to denote the matching mate foru,where the edge[u,u′]∈M.IfGis a bipartite graph with a unique perfect matching then it is nonsingular(see[2]).

A unicyclic graphGis a connected simple graph which satisfies|E(G)|=|V(G)|.A bicyclic graphGis a connected simple graph which satisfies|E(G)|=|V(G)|+1.There are two type of basic bicyclic graphs:∞-graphs andθ-graphs.More concisely,an∞-graph,denoted by∞(p,q,l),is obtained from two vertex-disjoint cyclesCpandCqby connected one vertex ofCpand one ofCqwith a pathPlof lengthl−1(in the case ofl=1,identifying the above two vertices);and aθ-graph,denoted byθ(p,q,l),is a union of three internally disjoint pathsPp+1,Pq+1,Pl+1of lengthp,q,lrespectively with common end vertices,wherep,q,l≥1 and at most one of them is 1.Observe that any bicyclic graphGis obtained from an∞-graph or aθ-graph by attaching trees to some of its vertices(see[15]).

One motivation for considering a connected bipartite graph with a unique perfect matching is that in some cases in quantum chemistry,an H¨uckel graph can be considered as a connected bipartite graph with a unique perfect matching.

We sayλis an eigenvalue ofGifλis an eigenvalue ofA(G).We useσ(G)to denote the spectrum ofG.

In 1976,the notion of an inverse graph was introduced by Harary and Minc(see[5]).A nonsingular graphGis invertible ifA(G)−1is a matrix with entries from{0,1},and the graphHwith adjacency matrixA(G)−1is called the inverse graph ofG.However,in the same article,when only one connected graph is invertible,the author proved that a connected graphGis invertible if and only ifG=P2.In 1985,another notion of an inverse graph was supplied by Godsil(see[2]).This concept generalizes the definition given by Harary and Minc.

LetHdenote the class of connected bipartite graphs with unique perfect matchings.LetG∈H,thenA(G)−1is signature similar to a nonnegative matrix,that is,there exists a diagonal matrixSwith diagonal entries from{1,−1}such thatSA(G)−1S≥0.The weighted graph associated to the matrixSA(G)−1S≥0 is called the inverse ofGand is denoted byG+.A invertible graphGis said to be a self-inverse graph ifGis isomorphic to its inverse graph.LetHgdenote the class of connected bipartite graph with unique perfect matchingMsuch thatG/Mis bipartite.

Definition 1[7]LetG∈H,thenGhas at least two pendant(degree one)vertices.An edge of a graph is said to be pendant if one of its vertices is a pendant vertex.

A corona graphG◦K1is a graph which is obtained from a graphGby adding a new pendant vertex to every vertex ofG.

Some other notions about inverse graphs are introduced in the following literatures.In 1978,Cvetković,Gutman and Simić introduced the pseudo-inverse of a graph.LetGbe a graph.The pseudo-inverse graphPI(G)ofGis the graph,defined on the same vertex set asG,in which the verticesxandyare adjacent if and only ifG−x−yhas a perfect matching(see[3]).In 1988,Buckley,Doty and Harary introduced the signed inverse of a graph(see[11]).A signed graph is a graph in which each edge has a positive or negative sign(see[4]).An adjacency matrix of a signed graph is symmetric and entries from{0,1,−1}.A nonsingular graphGhas a signed inverse ifA(G)−1is the adjacency matrix of some signed graphH.In 1990,Pavlíkovand Jediný introduced another notion of inverse graphs.The inverse of a nonsingular graph with the spectrumλ1,λ2,···,λnis a graph with the spectrum(see[14]).This type of inverse of a graph should not be unique.In this article,we follow the notion of inverse graph given by Godsil.

In[2],Godsil introduced the notion of a graph inverse and supplied a classHgofHwhich posses inverses.He posed the problem of characterizing the graphs inHwhich possess inverses.In[9],utilizing constructions derived from the graph itself,Tifenbach and Kirkland supplied necessary and sufficient conditions for graphs inHto possess inverses.In[1],Akbari and Kirkland provided a complete characterization of a unicyclic graph inHwhich possesses inverses.In[6],Panda and Pati supplied a large class of graph inHfor whichG+exists.The characterization of finding a graph with an inverse inHis still open.

Consider the problem of characterizing a graph which is isomorphic to its inverses inH.In[8],Simion and Cao showed that for anyG∈Hg,we have+if and only ifGis a corona graph.In[10],Tifenbach supplied necessary and sufficient conditions for graph satisfying+via a particular isomorphism inH.In[9],Tifenbach and Kirkland obtained necessary and sufficient conditions for an invertible unicyclic graph inHto be self-inverse.

In[9],Tifenbach and Kirkland supplied necessary and sufficient conditions for an invertible unicyclic graph inHsatisfying thatG+is unicyclic.In[13],Panda and Delhi supplied necessary and sufficient conditions for an invertible unicyclic graph inHsatisfying thatG+is bicyclic.Considering this result,we can naturally ask the following question.Can we characterize the bicyclic graphsGinHsuch thatG+is unicyclic or bicyclic?In this article,we supply such characterizations.

2 Preliminaries

In order to study inverse graphs better,the concepts of odd type and even type nonmatching edges were proposed by Panda and Pati(see[6]).

Definition 2[6]LetG∈H,a pathP=[u1,u2,···,u2k]is called an alternating path if and only if the edges[ui,ui+1]∈Mfor eachi=1,3,···,2k−1,and the other edges are nonmatching edges.We sayPis an mm-alternating path if[u1,u2],[u2k−1,u2k]∈M.We sayPis an nn-alternating path if[u1,u2],[u2k−1,u2k]∈E(G)M.

Definition 3[6,12](a)LetG∈Hand[u,v]∈E(G)M.An extension at[u,v]is called even type(resp.odd type)if the number of nonmatching edges on that extension is even(resp.odd).

(b)Let[u,v]∈E(G)M.We say[u,v]is an even type edge,if each extension at[u,v]is even type.We say[u,v]is an odd type edge,if either each extension at[u,v]is odd type or there are no extensions at[u,v].We say[u,v]is a mixed type edge,if it has an even type and an odd type extensions.

Example 1Consider the graphGshown in Figure 1.LetG∈H.is an even type edge,becauseare two even type extensions atEvery other nonmatching edge is an odd type edge.

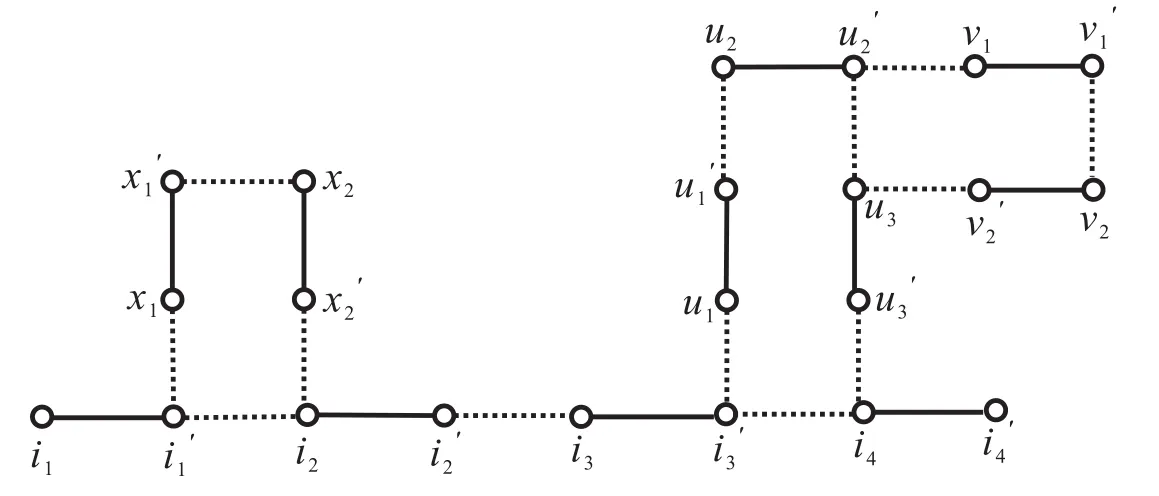
Figure 1:The solid edges are matching edges

3 Bicyclic Graphs with Possess Unicyclic or Bicyclic Inverses

The inverse graphG+of an unweighted graphGmay be weighted.In this section,we characterize the bicyclic graphGinHsuch thatG+is unicyclic or bicyclic,that is,G+is an unweighted connected unicyclic or bicyclic graph.

3.1 Bicyclic graphs in Hg

Remark 1[6]LetG∈Hg,then the following points are true.

(1)Each nonmatching edge is odd inG.

(2)Let[i,j]∈E(G+),the inverse graphG+ofGis an unweighted if and only if the number of mm-alternatingi−j-paths is at most one.

Next we present the inverse of the adjacency matrix of a graph inHgiven in[1].We follow the convention that sum over an empty set is zero.

Lemma 1[1]Let G∈H,and B=[bij],

where P(i,j)is the set of mm-alternating i−j-paths in G and∥P∥is the number of edges in P.Then B=A(G)−1.

Theorem 1[12]Let G∈Hg.Then the following are equivalent.

(1)+.

(2)|PG|=|E(G+)|,where PGis the set of mm-alternating paths in G.

(3)G=G1◦K1,for some connected bipartite graph G1.

The following is a description of a unicyclic or bicyclic graph as the inverse of a bicyclic graph.

Theorem 2Let G∈Hgbe bicyclic.There is no G+which is unicyclic.

ProofSinceG∈Hg,G+exists.First we considerG∈HgandGis a bicyclic graph onnvertices,so the number of matching edges isand the number of nonmatching edges is.SinceG+is unweighted,Remark 1 yields that there is at most one mm-alternating path inGfrom one vertex to another vertex.By Lemma 1,we havefor each nonmatching edge[u,v]inG.for each matching edge[u,u′]inG.Hence,G+has at leastn+1 edges,so there is noG+which is unicyclic.The proof is completed.

Theorem 3Let G∈Hgbe bicyclic.Then G+is bicyclic if and only if GG+.

ProofSinceG∈Hg,G+exists.First we assume thatG+is a bicyclic graph onnvertices,Remark 1 yields that there is at most one mm-alternating path inGfrom one vertex to another vertex.Ghas no mm-alternating path of length 5,otherwise by Lemma 1 and Theorem 1G+has at leastn+2 edges,which is not possible.Then the length of each mm-alternating path inGis either 1 or 3.Using this fact one can easily show that each matching edge inGis a pendant edge.HenceGis a corona graph,by Theorem 1,+.

Conversely,if+,it is clear thatGis bicyclic,thenG+is also bicyclic.The proof is completed.

3.2 Bicyclic graphs in HHg

In this subsection,we characterize the bicyclic graphsG∈HHgsuch thatG+is unicyclic or bicyclic.

Corollary 1[1]Let G∈H,and A(G)be its adjacency matrix.Then A(G)−1is diagonally similar to a nonnegative matrix if and only if the product of the edge weights on any cycle in G+is1.

In[6],a class is supplied for whichG+exists.It is the class inHin which each nonmatching edge is either even type or odd type and such that the extensions at two distinct even type edge never have an odd type edge in common.We shall denote this class byF.LetG∈Handεbe the set of all even type edges inG.The author proved that forG∈F,G+exists if and only if(G−ε)/Mis bipartite.

LetG∈HHgbe a bicyclic graph.It is clear thatGhas either one even type extension,or two even type extensions.

(a)IfGhas exactly one even type extension,it is clear thatG∈Fsuch that(G−ε)/Mis bipartite,thenG+exists.

(b)IfGhas exactly two even type extensions,it is clear thatG∈Fsuch that(G−ε)/Mis bipartite,thenG+exists.

(a)IfGhas exactly one even type extension.

(1)There is no mixed type edge inG.We are not sure whether the inverse of this graph exists.But we can give two examples of such graphs as shown in Figure 2,where the inverse of Figure 2(a)exists,the inverse of Figure 2(b)does not exist.

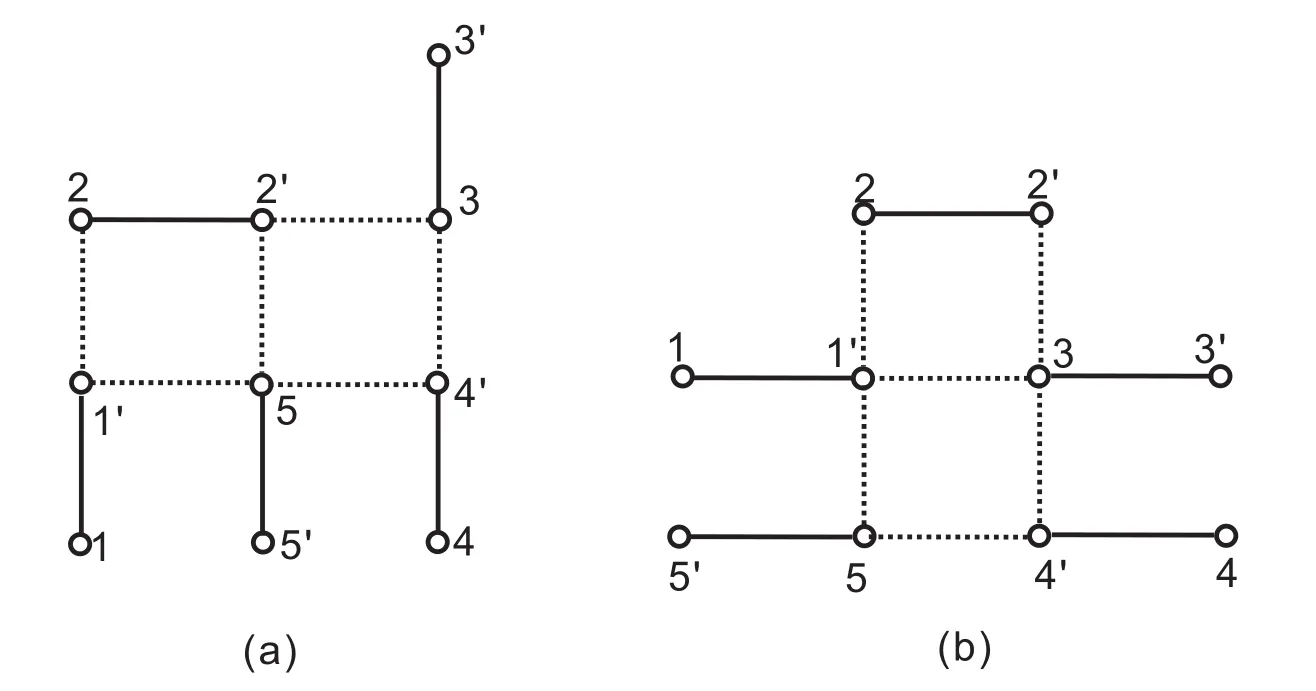
Figure 2:The solid edges are matching edges

Example 2Consider the graph shown in Figure 2(a).The graphG∈Fand(G−ε)/Mis bipartite,thenG+exists.The graphGhas an inverse whereS=diag[1,−1,1,−1,1,1,−1,1,−1,1].In particular,this graph is aθ-graph with bicyclic inverse.

Consider the graph shown in Fig 2(b).This graphG+does not exist.To see this putB=A(G)−1.IfG+exists,by Corollary 1,for cycle[1,2′,2,3′,4,5′,1],we must haveB(1,2′)B(2′,2)B(2,3′)B(3′,4)B(4,5′)B(5′,1)=1,which is not possible,becauseB(1,2′)=B(2,3′)=B(3′,4)=B(4,5′)=B(5′,1)=−1 andB(2′,2)=1.

(2)There is a mixed type edge,which has an even type extension and an odd type extension.We are not sure whether the inverse of this graph exists.But we can give an example of such a graph as shown in Figure 3,whose inverse does not exist.

Figure 3:The solid edges are matching edges

Example 3Consider the graph shown in Figure 3.This graphG+does not exist.To see this putB=A(G)−1.Note thatB(1,1′)=1 andB(1′,5)=B(5,2′)=B(2′,1)=−1.By Corollary 1,we know that ifG+exists,for cycle[1,1′,5,2′,1],we haveB(1,1′)B(1′,5)B(5,2′)B(2′,1)=1,which is not the case here.

(b)IfGhas exactly two even type extensions.

(1)Ghas exactly one even type edge with two even type extensions,it is clear thatG∈Fsuch that(G−ε)/Mis bipartite,thenG+exists.

(2)Ghas exactly two even type extensions on two distinct even type edges.We are not sure if the inverse of this graph exists.But we can give two examples of such graphs as shown in Figure 4,where the inverse of Figure 4(a)does not exist,the inverse of Figure 4(b)exists.

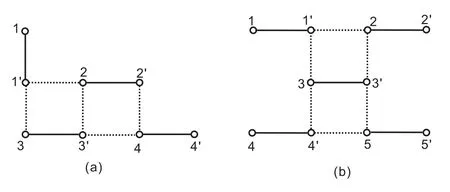
Figure 4:The solid edges are matching edges

Example 4Consider the graph shown in Figure 4(a).The graphG+does not exist.To see this putB=A(G)−1.IfG+exists,by Corollary 1,we must haveB(3,2′)B(2′,2)B(2,4′)B(4′,3)=1 for the cycle[3,2′,2,4′,3],which is not possible,becauseB(3,2′)=B(2,4′)=B(4′,3)=−1 andB(2,2′)=1.

In the graph shown in Figure 4(b).The graphG∈Fand(G−ε)/Mis bipartite,thenG+exists.The graphGhas an inverse whereS=diag[1,1,−1,1,1,1,1,−1,1,1].In particular,this graph is aθ-graph with bicyclic inverse.

(3)Ghas exactly two even type extensions on two distinct nonmatching edges which have a mixed type edge inG.We are not sure if the inverse of this graph exists.But we can give an example of such a graph as shown in Figure 5,whose inverse exists.

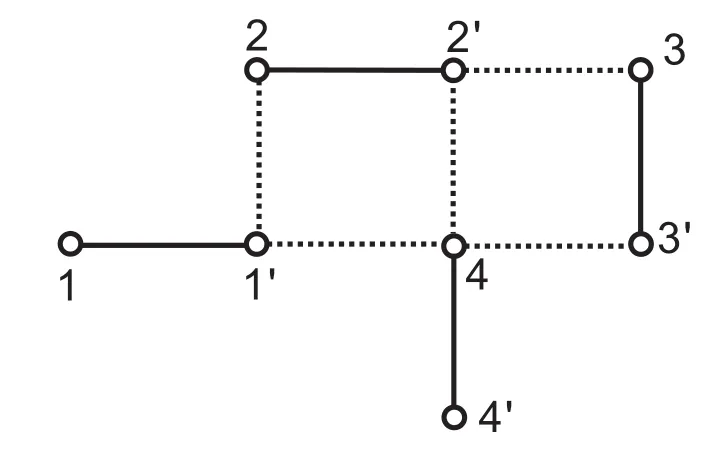
Figure 5:The solid edges are matching edges

Example 5Consider the graph shown in Figure 5.The edge[1′,4]is a mixed type edge,so.But the graphGhas an inverse whereS=diag[1,−1,1,−1,1,−1,1,−1].In particular,this graph is aθ-graph with bicyclic inverse.

Definition 4LetG∈H.A minimal path inGfrom a vertexuto a vertexvis a mm-alternatingu−v-path which does not contain an even type extension(at some nonmatching edge inG).A simple minimal path is a minimal path which does not contain an even type edge.

Example 6In the graphGshown in Figure 1,is an mm-alternating path fromi1toandis an mm-alternatingi1−i′4-path which is not a minimal path.

Lemma 2Let G∈HHgbe∞-graph.Assume that ε is the set of all even type edges in G.Then|E(G−ε)|≤|E(G+)|.

ProofLet[u,v]/∈εbe any nonmatching edge inG.By Lemma 1,there are mm-alternatingu′−v′-paths inGsuch thatA(G+)u′,v′0.For each matching edge[u,u′],by Lemma 1,we haveA(G+)u,u′0.Hence,for each edge[u,v]/∈εinG,there is an edge inG+.Thus|E(G−ε)|≤|E(G+)|.The proof is completed.

Lemma 3[13]Let G∈HHgbe an invertible bicyclic graph.Assume that ε is the set of all even type edges in G.Then G+has a nonmatching[u,v][u′,v′]is not in G if and only if G has a simple minimal u−v-path of length at least5.

Lemma 4Let G∈B be θ-graph,where B containsCase 2(b)(1),Then G+exists.Assume that G has exactly one even type edge with two even type extensions,and assume that[x,y]is an even type edge.Then|E(G)|≤|E(G+)|.

ProofLet[u,v][x,y]be any nonmatching edge inG.By Lemma 1,there is exactly one mm-alternatingu′−v′-path inGsuch thatA(G+)u′,v′̸0.For each matching edge[u,u′],by Lemma 1,we haveA(G+)u,u′̸0.Furthermore,by Lemma 1,we haveA(G+)x,y̸0 for the even type edge[x,y].Hence,for each edge[u,v]inG,there is an edge inG+.Thus|E(G)|≤|E(G+)|.The proof is completed.

Theorem 4Let G∈HHgbe∞-graph.Then G+is unicyclic if and only if:

(1)G has no simple minimal path of length5,when G has exactly one even type extension;

(2)G has exactly one simple minimal path of length5,when G has exactly two even type extensions.

ProofSinceG∈HHgis∞-graph,it contains two circles,at least one of which is composed of even type extension and even type edge,andG+exists.

(1)First we assume thatG+is unicyclic.We now show that whenGhas exactly one even type extension,Ghas no simple minimal path of length 5.Assume thatGhas one simple minimal path of length 5.Then by virtue of Lemmas 2 and 3,G+hasn+1 edges,which contradicts to the fact thatG+is unicyclic.ThenGhas no simple minimal path of length 5,whenGhas exactly one even type extension.

Conversely,whenGhas exactly one even type extension,Ghas no simple minimal path of length 5.By Lemmas 2 and 3,G+has exactlynedges.Hence,G+is unicyclic.

(2)Now we show that whenGhas exactly two even type extensions,Ghas exactly one simple minimal path of length 5.Assume thatGhas no simple minimal path of length 5.By Lemmas 2 and 3,G+hasn−1 edges,which contradicts to the fact thatG+is unicyclic.Suppose thatGhas two simple minimal paths of length 5,sayP1andP2,the set of end vertices ofP1is not equal to the set of end vertices ofP2.Using Lemmas 2 and 3,G+has at leastn+1 edges,which is not possible.ThenGhas exactly one simple minimal path of length 5,whenGhas exactly two even type extensions.

We now show the converse,whenGhas exactly two even type extensions,Ghas exactly one simple minimal path of length 5.By Lemmas 2 and 3,G+has exactlynedges.Hence,G+is unicyclic.The proof is completed.

Theorem 5Let G∈HHgbe∞-graph.Then G+is bicyclic if and only if:

(1)G has exactly one simple minimal path of length5,when G has exactly one even type extension;

(2)G has exactly two simple minimal paths of length5,when G has exactly two even type extensions.

ProofSinceG∈HHgis∞-graph,it contains two circles,at least one of which is composed of even type extension and even type edge,andG+exists.

(1)First we assume thatG+is bicyclic.We now show thatGhas exactly one simple minimal path of length 5,whenGhas exactly one even type extension.Assume thatGhas no simple minimal path of length 5.By Lemmas 2 and 3,G+hasnedges,which contradicts to the fact thatG+is bicyclic.HenceGhas at least one simple minimal path of length 5.Assume thatGhas two simple minimal path of length 5 sayP1andP2,the set of end vertices ofP1is not equal to the set of end vertices ofP2.By Lemmas 2 and 3,G+has at leastn+2 edges,which is not possible.ThenGhas exactly one simple minimal path of length 5,whenGhas exactly one even type extension.

Conversely,whenGhas exactly one even type extension,Ghas exactly one simple minimal path of length 5.By Lemmas 2 and 3,G+hasn+1 edges.Hence,G+is bicyclic.

(2)We now show thatGhas exactly two simple minimal paths of length 5,whenGhas exactly two even type extensions.Assume thatGhas no simple minimal path of length 5.Then by virtue of Lemmas 2 and 3,G+hasn−1 edges,which contradicts to the fact thatG+is bicyclic.Suppose thatGhas three simple minimal paths of length 5,sayPifori=1,2,3,the set of end vertices ofPiis not equal to the set of end vertices ofPjfori,j=1,2 andi̸=j.Using Lemmas 2 and 3,we getG+hasn+2 edges,which is not possible.IfGhas exactly one simple minimal path of length 5,by Lemmas 2 and 3,G+hasnedges,which is not possible.HenceGhas exactly two simple minimal paths of length 5,whenGhas exactly two even type extensions.

Conversely,whenGhas exactly two even type extensions,Ghas exactly two simple minimal paths of length 5.By Lemmas 2 and 3,G+hasn+1 edges.Hence,G+is bicyclic.The proof is completed.

Theorem 6Let G∈B be θ-graph,where B contains Case2(b)(1).There is no G+which is unicyclic.

ProofSinceG∈B,thenG+exists.Ghas exactly two even type extensions.That is,Ghas exactly one even type edge with two even type extensions.By Lemma 4,G+has at leastn+1 edges.Hence there is noG+which is unicyclic.The proof is completed.

Theorem 7Let G∈B be θ-graph,where B contains Case2(b)(1).Then G+is bicyclic if and only if G has no simple minimal path of length5.

ProofSinceG∈B,thenG+exists.First we assume thatG+is bicyclic.We now show thatGhas no simple minimal paths of length 5,whenGhas exactly two even type extensions,that is,Ghas exactly one even type edge with two even type extensions.Assume thatGhas one simple minimal path of length 5.Then by virtue of Lemmas 3 and 4,G+has at leastn+2 edges,which is not possible.HenceGhas no simple minimal paths of length 5.

Conversely,ifG∈BandGhas no simple minimal path of length 5,by Lemmas 3 and 4,G+has exactlyn+1 edges.HenceG+is bicyclic.The proof is completed.

4 Conclusion

In[2],Godsil introduced the notion of a graph inverse and supplied a class of graphs inHwhich possess inverses.In[1],the authors provided a complete characterization of unicyclic graphs inHwhich possess inverses.In[9],the authors presented a characterization of unicyclic inHwhich possesses a unicyclic inverse.In[6],the authors supplied a lager class of invertible graph inHwhich properly contains those in Godsil[2].Here we presented a characterization of bicyclic graphs inHwhich possess unicyclic or bicyclic inverses.We divided the bicyclic graphs inHinto two subclasses which areHgandHHg.We characterized bicyclic graphs with unicyclic or bicyclic inverses inHg,and supplied a necessary and sufficient conditions for∞-graph inHHgto have unicyclic or bicyclic inverse.However,forθ-graph inHHg,we only give partial characterization.