TRAVELING WAVE SOLUTIONS FOR A PREDATOR-PREY MODEL WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE∗†
2020-09-14ZhuanlingGaoXiangkuiZhaoZhihongZhao
Zhuanling Gao,Xiangkui Zhao,Zhihong Zhao
(School of Mathematics and Physics,University of Science&Technology Beijing,Beijing 100083,PR China)
Abstract
Keywords predator-prey model;Beddington-DeAngelis;traveling wave solution;existence
1 Introduction
In recent years,we have found that some species are endangered by their predators or other reasons.This will cause ecologically bankrupt.Therefore we pay more attention to it.The predator-prey model is an important tool to study the relationship of several species.And it is a topic attracting more and more attention from mathematicians and ecologists[3,5–7,12,16].So it has very broad application prospects.Whether the predator and prey can survive eventually is equivalent to the existence of traveling wave solution for specific model.So the traveling wave solution has studied by many scholars,see[1,9,10,15,19,20]and their references.
In 2016,Chen,Yao,and Guo[4]studied the diffusion predator-prey model of Lotka-Volterra type functional response.The model is as follows:
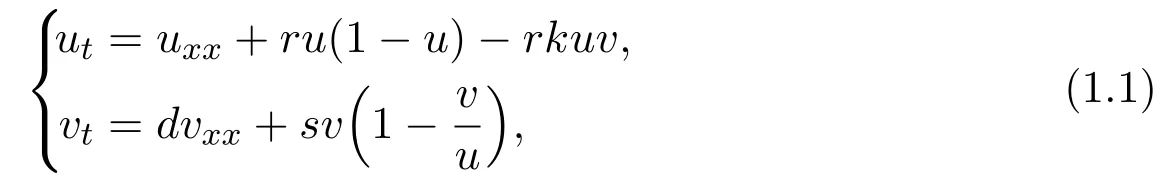
whereu,vrepresent the population densities of the prey and predator species at positionxand timet,respectively,d,r,s,kare constant numbers,dis the diffusion coefficient,andr,sare the intrinsic growth rates of speciesu,v,respectively.The functional response of the predator to the prey is given by the Lotka-Volterra typerku.
Then,Zhao[20]studied the model ask=1,namely
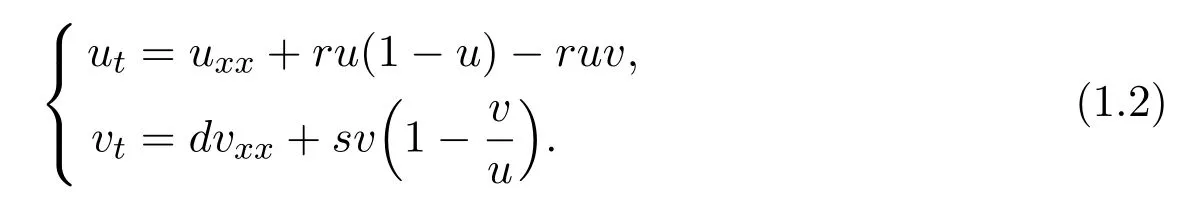
In 2017,Ai,Du,Peng[1]studied the traveling wave solution of the Holling-Tanner predator-prey model:
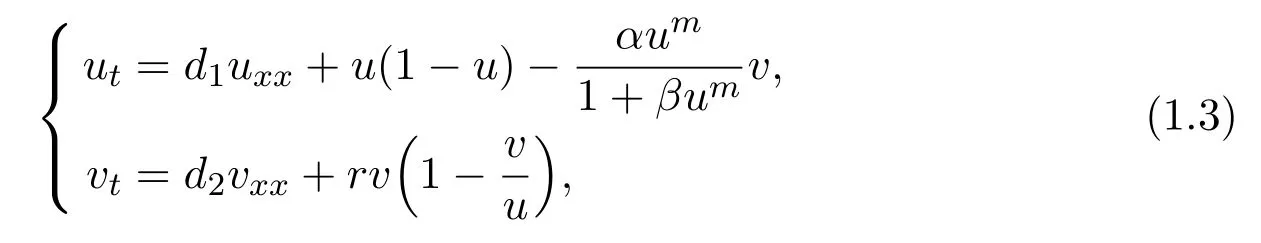
whereu,vrepresent the population densities of the prey and the predator at positionxand timet,respectively,the parametersα,mandrare positive andβis nonnegative.Here,the predation rate in the prey equation is controlled by a so-called Holling type functional response.The predator equation is also singular at zero prey population.Whenm=1,β=0,model(1.3)becomes model(1.2).
The functional response function of(1.3)is a class of Holling-II type functional response function only depending on the prey.However,in reality,it is not independent of predator either.In fact,the B-D functional response functionmaintains all the advantages of the ratio-dependent response function and avoids the controversy caused by the low-density problem,so it can better reflect the real relationship of the two species[8,11,17,18].Whenm1=0 andm2̸=0,the Beddington-DeAngelis type functional response is also a class of Holling-II type[13,14].
We will consider the following model:
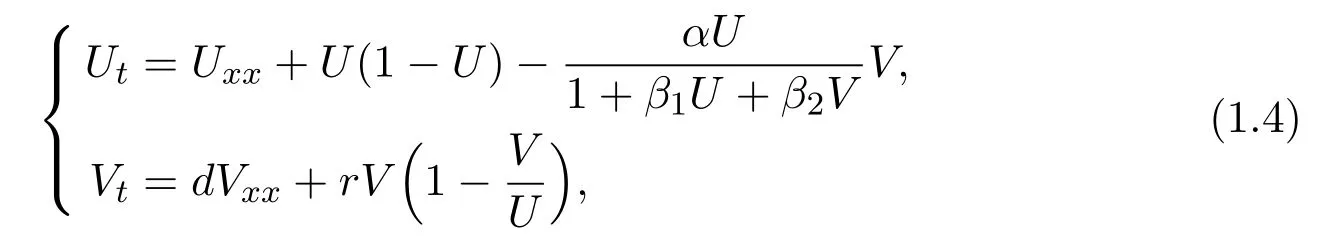
whereU,Vrepresent the population densities of the prey and the predator at positionxand timet,respectively,and the constantdis the diffusion coefficient corresponding toU,V.The parametersr,c,d,αare all normal andβ1,β2are nonnegative.ris the intrinsic growth rate of the prey.
It is easy to conclude that(1.4)has two equilibrium pointsE0=(1,0)andE∗=(U∗,V∗),where
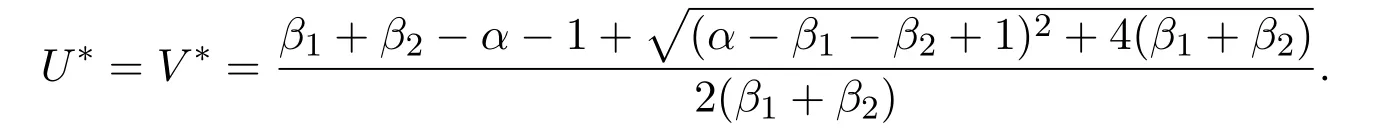
In this paper,we consider the case that the habitat is the entire spaceR.What we are interested in is if an exotic predator is introduced into the habitat of an existing prey,whether the predator and prey can eventually survive.In fact,this problem is equivalent to whether the solution of(1.4)tends to be the only positive constant steady state as time approaches infinity.Therefore,we study the traveling wave solution as below.
If there are positive functionsuandvdefined onRsuch thatU(x,t)=u(x+ct),V(x,t)=v(x+ct),then the solution of(1.4)is called the traveling wave of speedc.Hereu,vis the waveforms,setz=x+ctand bring(U,V)(x,t)=(u,v)(z)into(1.4).Then the traveling wave satisfies the following system of equations:
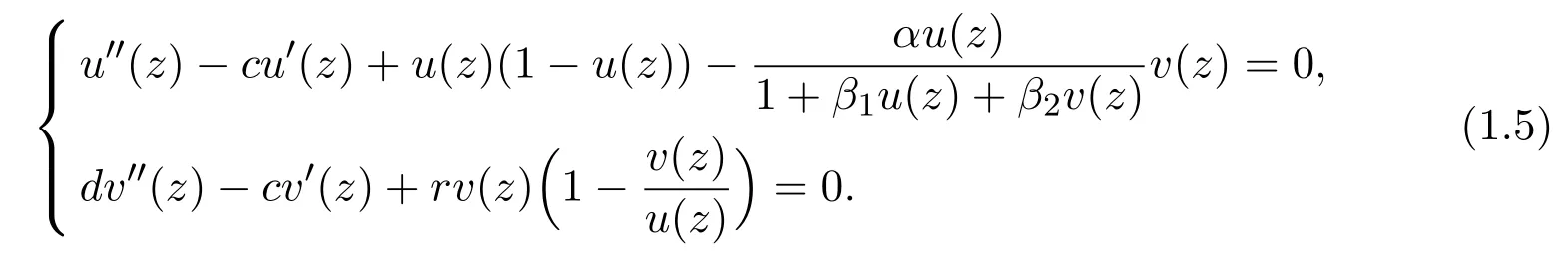
As above,this paper mainly considers the traveling wave solutions of connections(1,0)to(U∗,V∗).It means that(u,v)satisfies the following condition
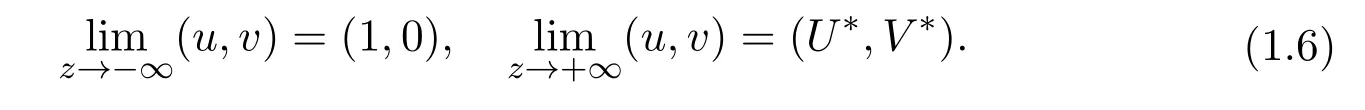
In order to overcome the singularity of the predator equation,an auxiliary system of(1.5)similar to[1]was introduced.
The rest of the paper is organized as follows:In the second section,an auxiliary system is introduced.We construct a pair of upper and lower solutions of the auxiliary system and study the existence of the weak traveling wave solutions of the auxiliary system by Schauder’s fixed point theorem.Here,the weak traveling wave solution means that the solution is connected(1,0)atz→−∞,but atz→+∞is not necessarily connected(U∗,V∗).By proving thatu(z)has a lower bound,we know the weak traveling wave of the auxiliary system is the weak traveling wave of the original model.In the third section,we use a squeeze method to prove that the weak traveling wave is actually a traveling wave.That is,And the traveling wave solution of the original model is obtained.In the forth section,some simulations are given for the theoretical results by Matlab.Nonexistence of traveling waves solutions is proved in Section 5.Finally,we give the details of the verifications of all constructed upper and lower solutions in Supplementary.
For convenience,we will usexinstead of variablezbelow.
2 The Solutions of Auxiliary System
To overcome the singularity of predator equation,we introduce the following auxiliary system[1]:
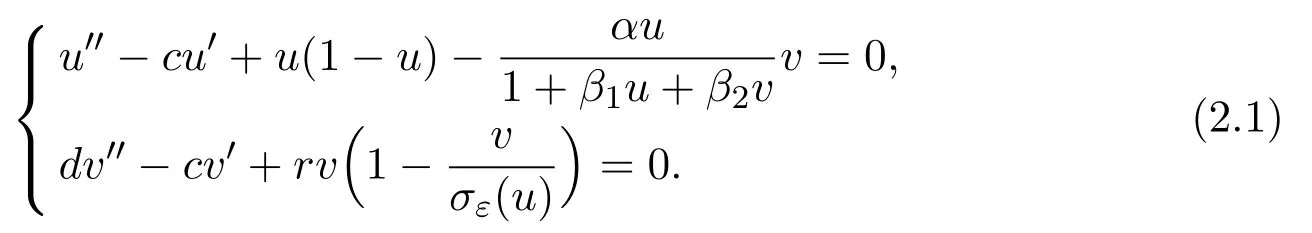
Here we replace the reaction functionwith a smooth funtion,where
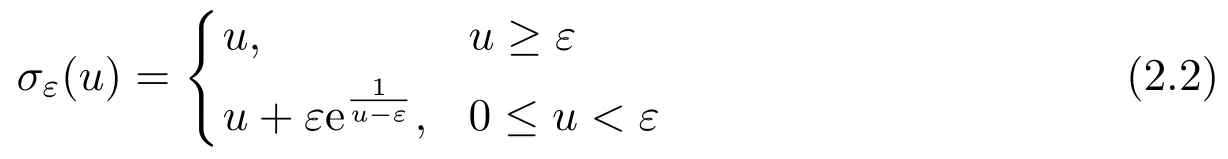
withε>0 sufficiently small.
2.1 Upper and lower solutions
First,we give the definition of upper and lower solutions of system(2.1)as follows.
Definition 2.1The functionsandare called a pair of upper and lower solutions of(2.1),ifare bounded and the inequalities
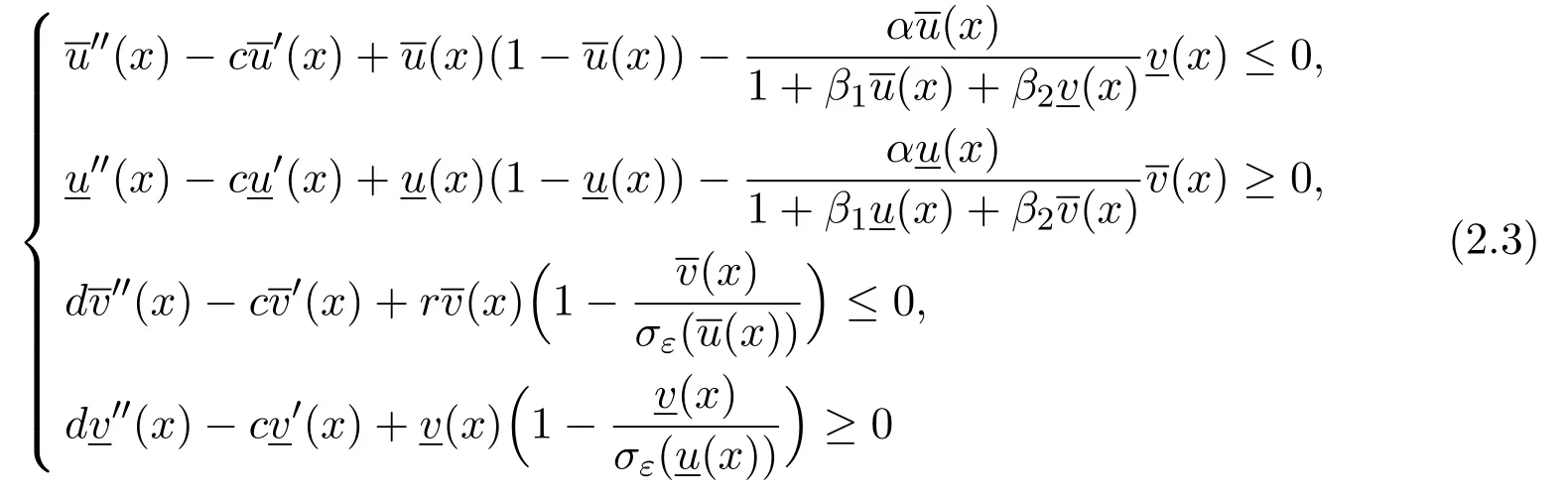
hold forx∈RDwith some finite setD={x1,···,xm}.
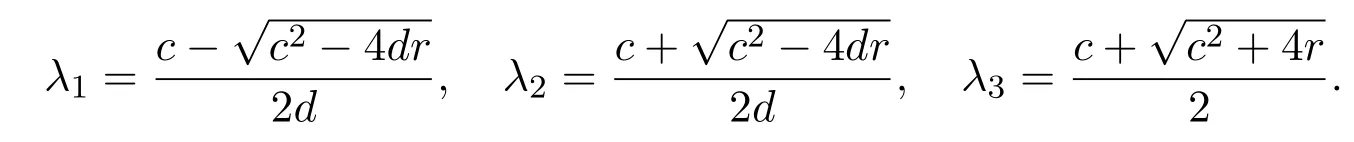
In fact,we have
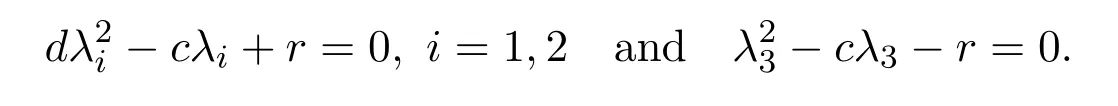
Next,to consider the existence of upper and lower solutions of(2.1),we divide it into two cases:c>c∗andc=c∗.
2.1.1 The casec>c∗
First,for given constantsA>1,η>0,we consider a function
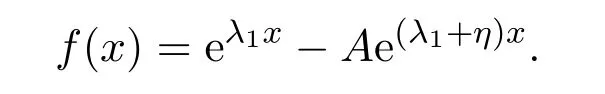
Then it is easy to check that the function has a unique zero point atand a unique maximum point atAndfis continuous on R and positive on(−∞,z0).
Next,we choose the constantsη,γ,β,α,β1,β2andAsatisfying the following conditions
(A1)η∈(0,min{λ1,λ2−λ1}),γ>0 is small enough such thatγ<λ1andγ2−cγ<0;
(A4)0<α − β2<1,β1>β2.
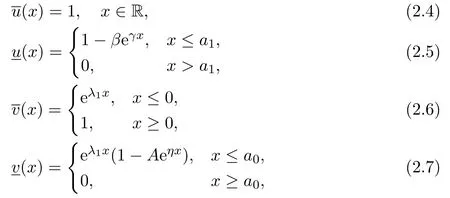
Lemma 2.1Assume that c>c∗,then the functionsdefined by(2.4)-(2.7)are a pair of upper and lower solutions of(2.1).
For the specific details about the proof of Lemma 2.1,we refer the readers to Supplementary of this paper.
2.1.2 The casec=c∗
In this subsection,we consider the existence of the upper and lower solutions of(2.1),whenIn this case,we haveFor given positive constantsIntroduce a function in[4]
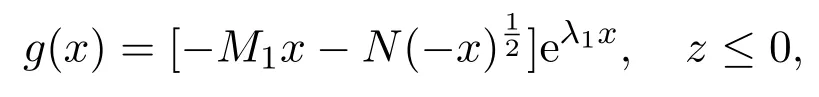
Next,we choose the constantsβ,γ,N,α,β1andβ2satisfying the following conditions:
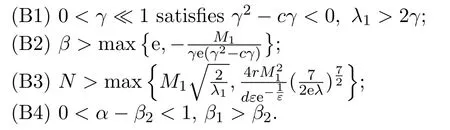
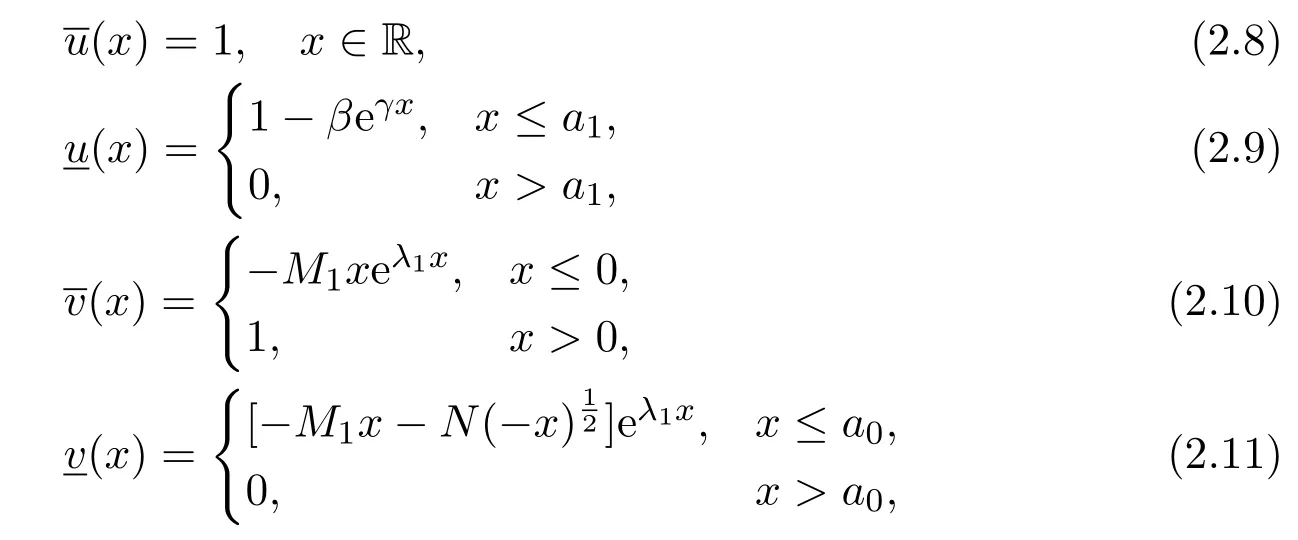
Lemma 2.2Assume that c=c∗,then the functionsdefined by(2.8)-(2.11)are a pair of upper and lower solutions of(2.1).
For the specific details about the proof of Lemma 2.1,we refer the readers to Supplementary of this paper.
2.2 Existence of weak traveling wave solutions
According to the form of the upper and lower solutions constructed in the previous text,we will use the Schauder’s fixed point theorem to prove the existence of solution of system(2.1)in this section.
First,we introduce the following function spaces

thenXis a Banach space equipped with the standard supremum norm.In the paper,we use the standard partial ordering and order intervals in R or R2,and apply∥·∥to denote the norm in R2.Further define
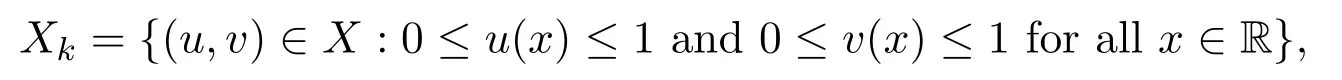
Next,define functions
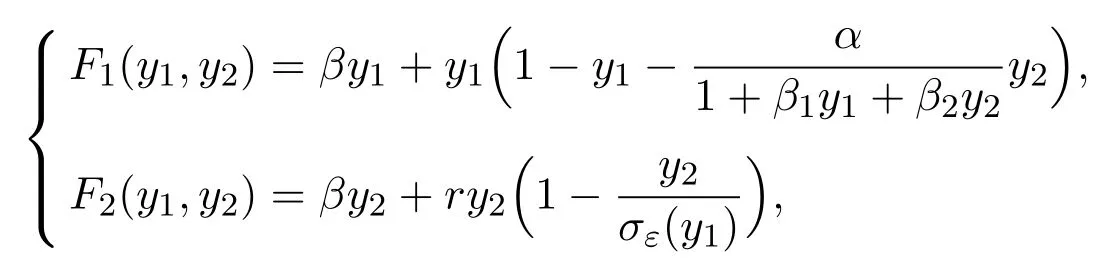
for some constantβ.Bywe get thatF1is nondecreasing iny1and is decreasing iny2forδ0≤y1≤1 and 0≤y2≤1.At the same time,F2is nondecreasing with respect toy1andy2forδ0≤y1≤1 and 0≤y2≤1.
Now we define
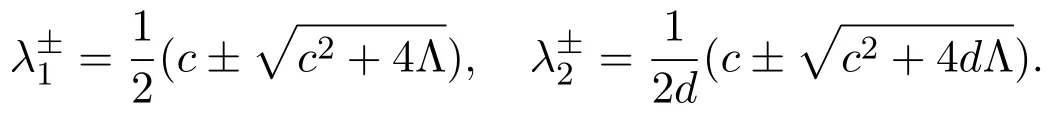
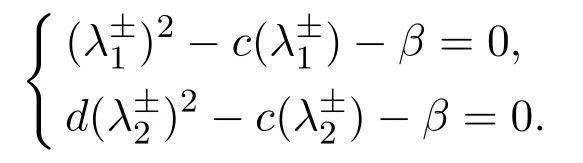
For Φ =(ϕ1,ϕ2)∈Xk,define an operatorP=(P1,P2):Xk→Xas follows:
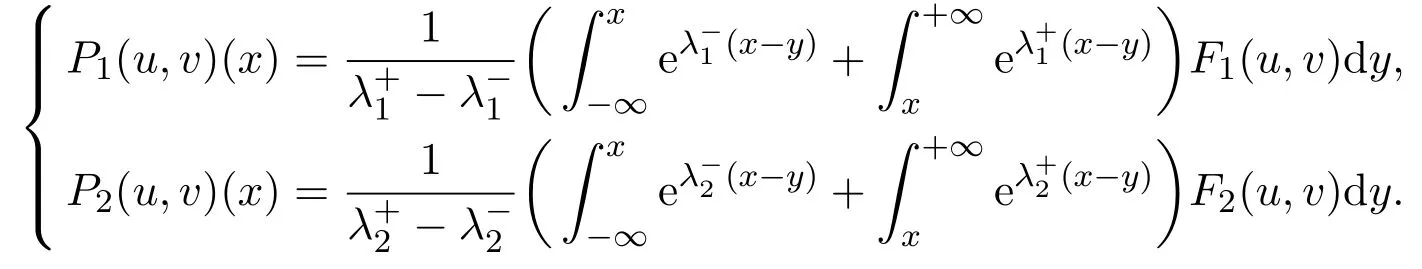
It is easy to see the operatorP=(P1,P2):Xk→Xis a solution of(2.1).
Lemma 2.3Let c≥c∗.Assume thatin Xkis a pair of upper andlower solutions of(2.1)satisfying
Then(2.1)has a positive solution(u,v)such thatx∈R.
The proof can be shown by a similar argument as in[4].We will not repeat it here.
Theorem 2.1Assume that c≥c∗,there is a set of positive solutions(u,v)in(2.1)such thatandx∈R.
ProofFirst we prove that the casec>c∗.By Lemma 2.1,we know that(2.4)-(2.7)are a pair of upper and lower solutions of(2.1).Now we show that conditions(1)and(2)in Lemma 2.3 hold for the casec>c∗.Whenx≥a1,we have
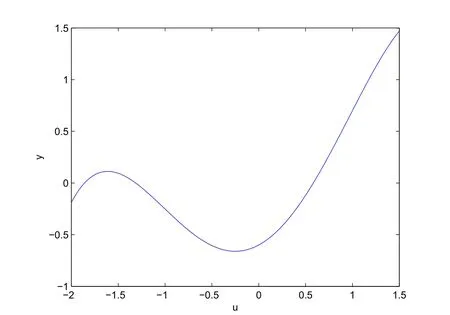
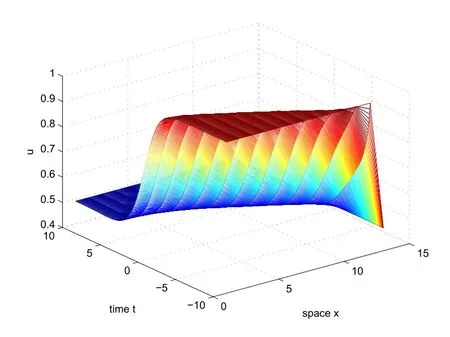
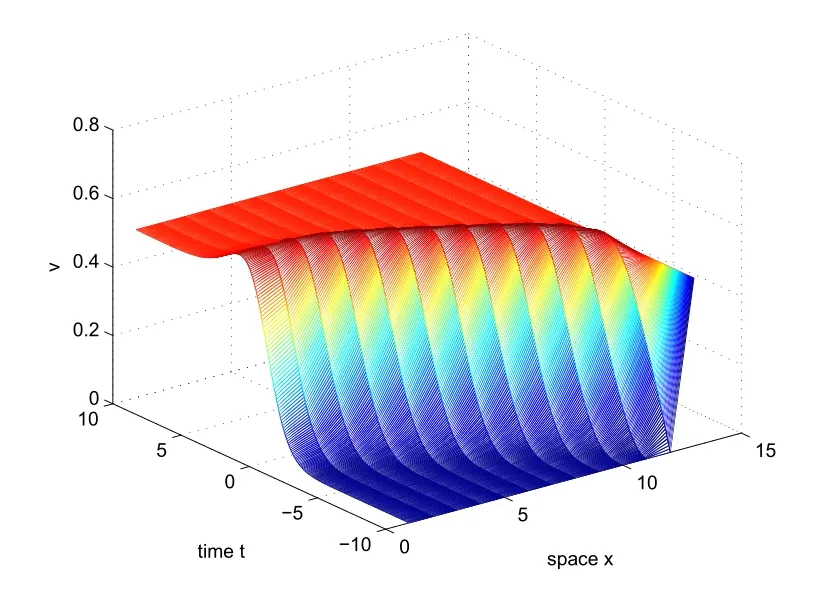
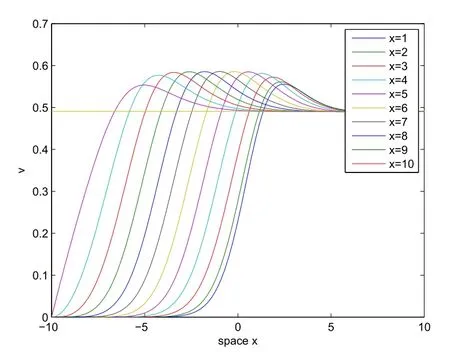
Whenx Thus there exists a pair of functions with Based on the above theorem,we show that the prey component in this weak traveling wave solution has a positive lower bound,that is: Theorem 2.2u(x)≥ε for x∈R. Proof Define aδ0,whereδ0is a positive solution of here we letε<δ0.Assume(u(x),v(x))to be a weak traveling wave solution of(2.12).Here we know 0 We complete the proof in four steps. meansT(x)→−∞asx→x1for some finite valuex1>x0.ThereforeT1(x)→∞asx→x2for somex2∈[x0,x1],a contra diction.It derives thatT1(x)is defined for allx∈R.To sum up,we know thaton R. The proofs of Steps 2 and 3 are similar to Lemma 2.3 in[10].We omit them here. For contradiction,we suppose thatu(x)≤εfor somex∈R.Then sinceu(−∞)=1 there is a smallestx0such thatu(x0)=εandu′(x0)≤0.According theu-equation of(2.1),since from Step 3,then Thus we deduce from the choices ofεandδ0,from which we conclude thatu′(x)≤0 and is not identical to 0 for allx>x0.This contradictsu(x)≥0.This showsu(x)>εforx∈R.The proof is complete. Consequentlyσε(u)≡u,thus the weak traveling wave solution of auxiliary system is the solution of the original model(1.5). In this section,we show that the solutions(u,v)converge to the coexistence equilibrium(u∗,v∗)asx→∞under additional conditions. Theorem 3.1For anyand the parameters satisfying0<α − β2<1,β1>β2,there exists a traveling solution(u,v)for(1.5)such that Here ProofBy Theorem 2.2,we know that the solution(u,v)of(2.1)satisfiesu(x)>εforx∈R.Therefore(1.5)has a positive solution satisfying(3.1)ifc≥c∗.Now we consider the tail behavior of the traveling wave for(1.5)at∞. Rewrite(1.5)to the following form Moreover,let the second iteration that isq(u)=h(h(u))−u=0.Simplify this equation,we have Here,we can see thatq(u)is a polynomial of degree 4 withq(±)=−∞,and Soq(u)=0 does not have any fixed point in the interval(0,1)other thanu=U∗.See Figure 1. According to[1],we also can define a similar sequenceas follows: Note thathis strictly monotone decreasing on[0,1]. Figure 1:y=q(u):parameters α =1.0, β1=0.7, β2=0.5. Next we apply the method of mathematical induction(see[1])to get the fact that there exists an increasing sequencewithxn→∞asn→∞such that,forx≥xn(n=0,1,2,···) Below we use matlab to further find the existence of the heteroclinic orbit between the two equilibrium points,that is,the traveling wave solution corresponding to system(1.5).Further we verify the theoretical results we have obtained. Figure 2 shows the traveling wave solution of the prey populationu(x,t)tends to the positive equilibrium point(U∗,V∗)with parametersα=1.0,β1=0.7,β2=0.5;Figure 3 is the traveling wave solution of the prey population in different positions.Figure 4 shows that the traveling wave solution of the predator populationv(x,t)tends to the positive equilibrium point(U∗,V∗)with parametersα=1.0,β1=0.7,β2=0.5;Figure 5 is the traveling wave solution of the predator population in different positions. In this section,we will show the nonexistence of solutions for(1.5)by use some conclusions of[2,4]. Theorem 5.1For any speed c Figure 2:The relationship between u,x and t. Figure 3:The relationship between v,x and t. Figure 4:The relationship between t and u in different positions. Figure 5:The relationship between t and v in different positions. ProofAssume the statement does not hold,then there exists somec1 By(1.6)and the positivity ofv,there exists a positive constantκsuch thatα(x,t):=v(x+c1t)satisfies a contradiction.Therefore,the proof of this theorem is completed.
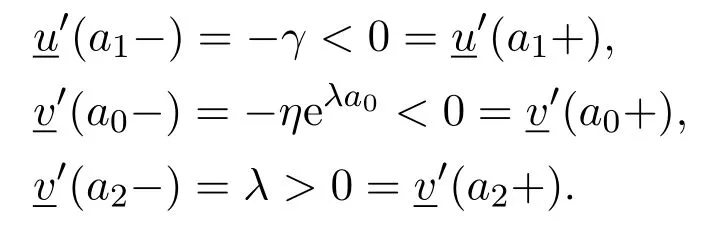
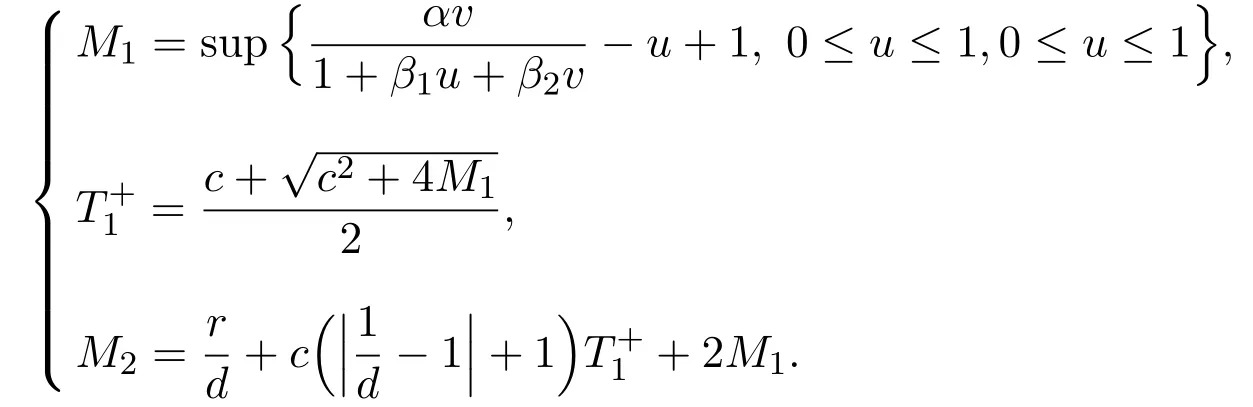
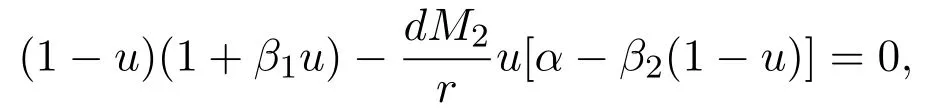
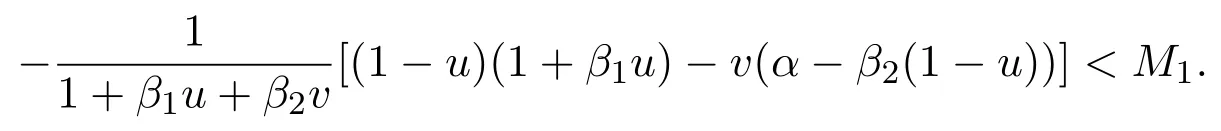
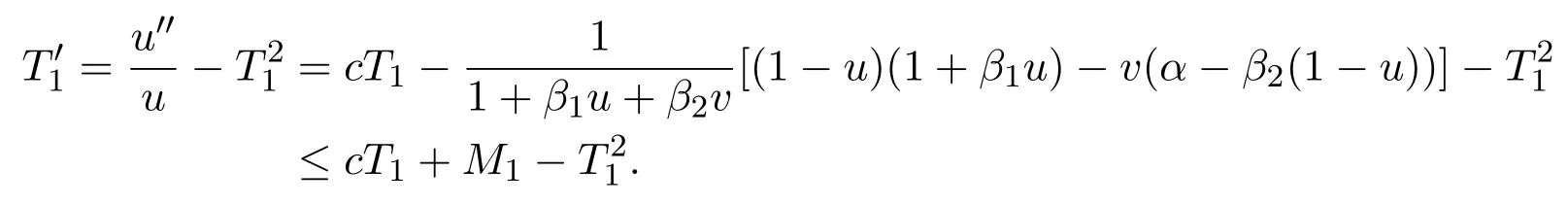
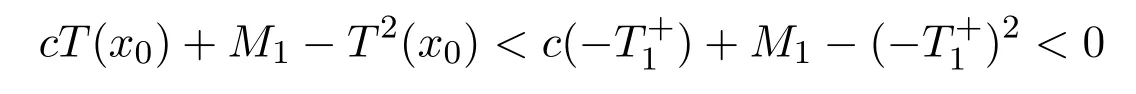
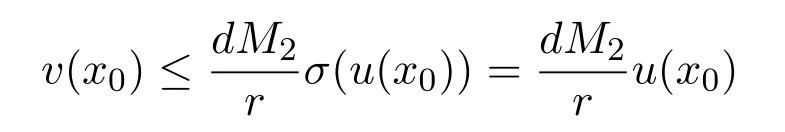
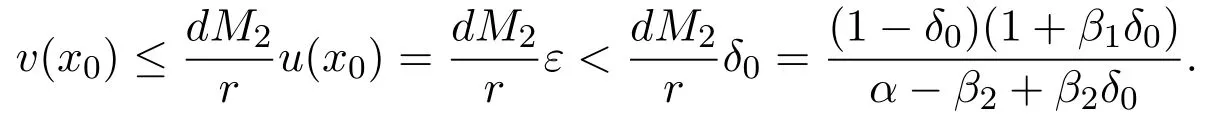
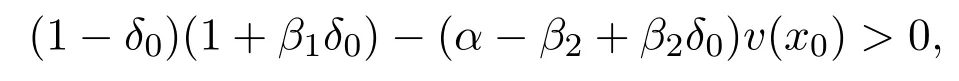
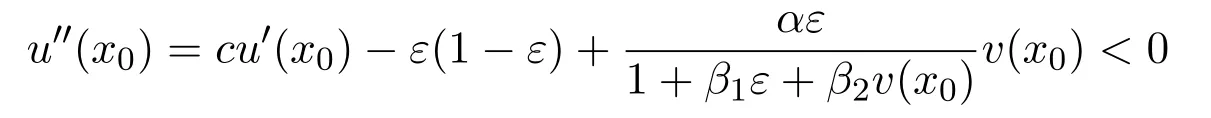
3 The Traveling Wave Solutions
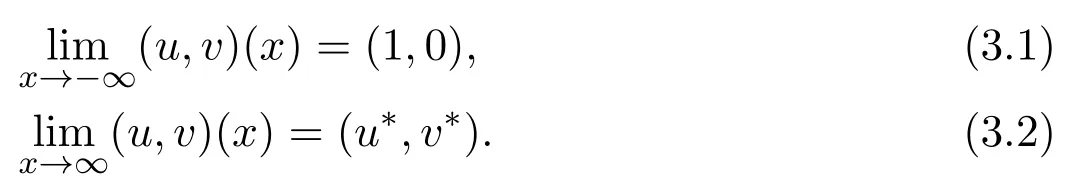
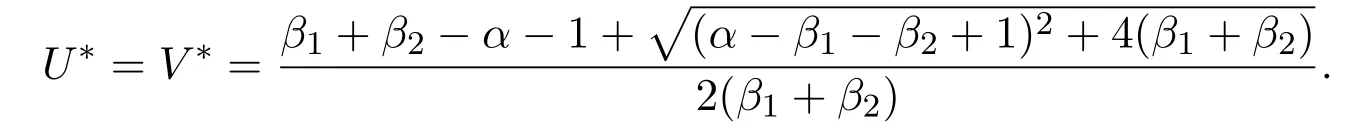
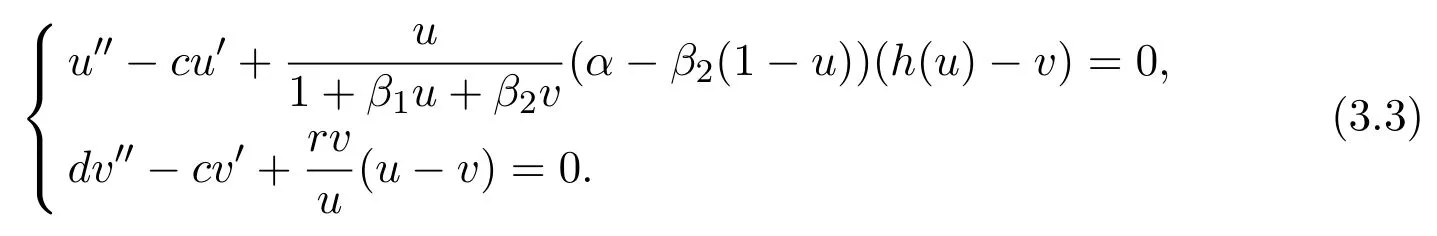
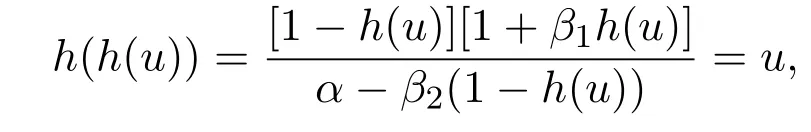
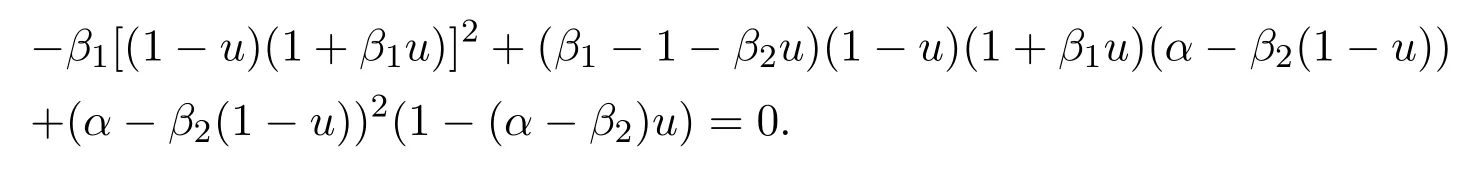
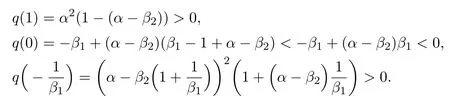
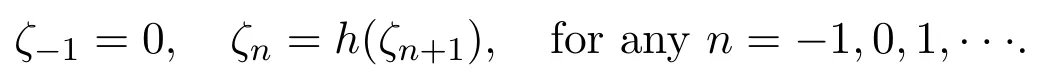
4 Numerical Simulation
5 Nonexistence of Traveling Waves

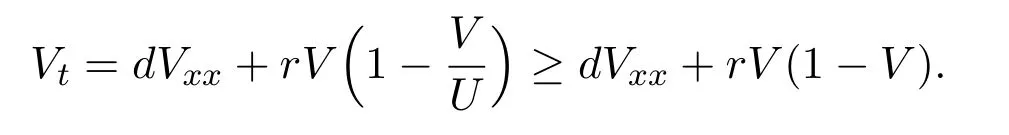
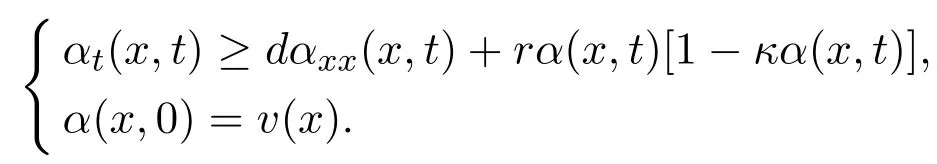
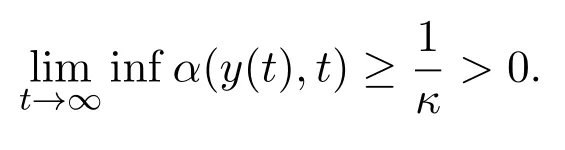
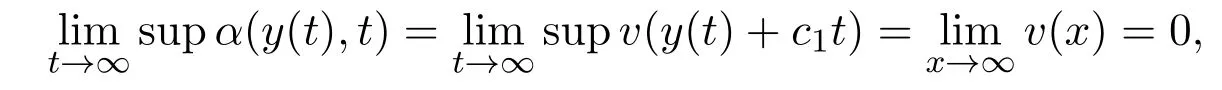
杂志排行
Annals of Applied Mathematics的其它文章
- THE EFFECT OF REFUGE AND PROPORTIONAL HARVESTING FOR A PREDATOR-PREY SYSTEM WITH REACTION-DIFFUSION∗†
- POSITIVE SOLUTIONS TO A BVP WITH TWO INTEGRAL BOUNDARY CONDITIONS∗†
- UNSTEADY NATURAL CONVECTIVE BOUNDARY LAYER FLOW AND HEAT TRANSFER OF FRACTIONAL SECOND-GRADE NANOFLUIDS WITH DIFFERENT PARTICLE SHAPES∗†
- BICYCLIC GRAPHS WITH UNICYCLIC OR BICYCLIC INVERSES∗†
- BIFURCATION ANALYSIS OF A CLASS OF PLANAR PIECEWISE SMOOTH LINEAR-QUADRATIC SYSTEM∗†
- NEW OSCILLATION CRITERIA FOR THIRD-ORDER HALF-LINEAR ADVANCED DIFFERENTIAL EQUATIONS∗†
