NEW OSCILLATION CRITERIA FOR THIRD-ORDER HALF-LINEAR ADVANCED DIFFERENTIAL EQUATIONS∗†
2020-09-14JianliYaoXiaopingZhangJiangboYu
Jianli Yao,Xiaoping Zhang,Jiangbo Yu
(School of Science,Shandong Jianzhu University,Ji’nan 250101,Shandong,PR China)
Abstract
Keywords third-order differential equation;advanced argument;oscillation;asymptotic behavior;noncanonical operators
1 Introduction
In 2019,Chatzarakis([1])o ff ered sufficient conditions for the oscillation and asymptotic behavior of second-order half-linear differential equations with advanced argument of the form
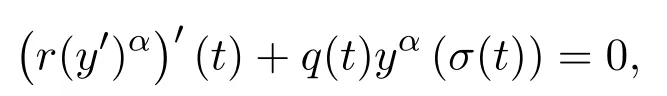
In 2018,Džurina([2])presented new oscillation criteria for third-order delay differential equations with noncanonical operators of the form

In this paper,we consider the oscillatory and asymptotic behavior of solutions to the third-order half-linear advanced differential equations of the form

Throughout the whole paper,we assume that
(H1)α,βandγare quotients of odd positive integers;
(H2)the functionsr1,r2∈C([t0,∞),(0,∞))are of noncanonical type(see Trench[2]),that is,
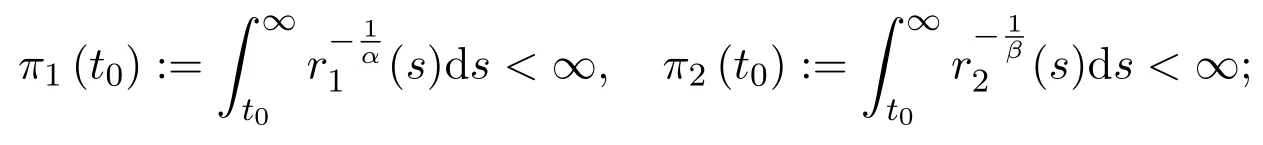
(H3)q∈C([t0,∞),[0,∞))does not vanish eventually;
(H4)σ∈C1([t0,∞),(0,∞)),σ(t)≥t,σ′(t)≥0 for allt≥t0.
By a solution of equation(1.1),we mean a nontrivial real valued functiony∈C([Tx,∞),R),Tx≥t0,which has the property thaty,are continuous and differentiable for allt∈[Tx,∞),and satisfy(1.1)on[Tx,∞).We only need to consider those solutions of(1.1)which exist on some half-line[Tx,∞)and satisfy the condition
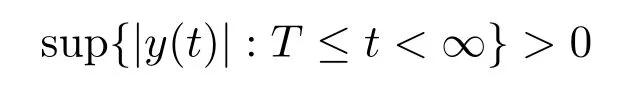
for anyT≥Tx.In the sequel,we assume that(1.1)possesses such solutions.
As is customary,a solutiony(t)of(1.1)is called oscillatory if it has arbitrary large zeros on[Tx,∞).Otherwise,it is called nonoscillatory.Equation(1.1)is said to be oscillatory if all its solutions oscillate.
Following classical results of Kiguradze and Kondrat’ev[3],we say that(1.1)has property A if any solutionyof(1.1)is either oscillatory or satisfieswhich is also called that equation(1.1)is almost oscillatory.
For brevity,we define operators
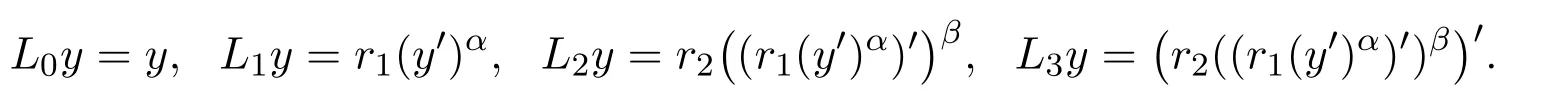
Also,we use the symbols↑and↓to indicate whether the function is nondecreasing and nonincreasing,respectively.
2 Main Results
As usual,all functional inequalities considered in this paper are supposed to hold eventually,that is,they are satisfied for alltlarge enough.
Without loss of generality,we need only to consider eventually positive solutions of(1.1),since ifysatisfies(1.1),so does−y.
The following lemma on the structure of possible nonoscillatory solutions of(1.1)plays a crucial role in the proofs of the main results.
Lemma 2.1Assume(H1)-(H4),and that y is an eventually positive solution of equation(1.1).Then there exists a t1∈[t0,∞)such that y eventually belongs to one of the following classes:

for t≥t1.
The proof is straightforward and hence is omitted.
Now,we will establish one-condition criteria of property A of(1.1).
Theorem 2.1Assume(H1)-(H4).If
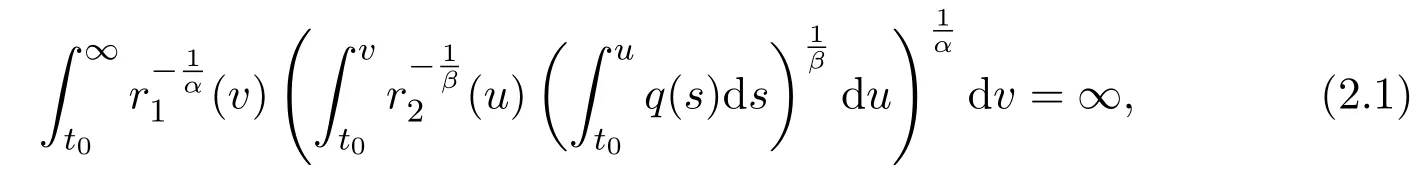
then(1.1)has property A.
ProofFirst of all,it is important to note that if(H2)and(2.1)hold,then
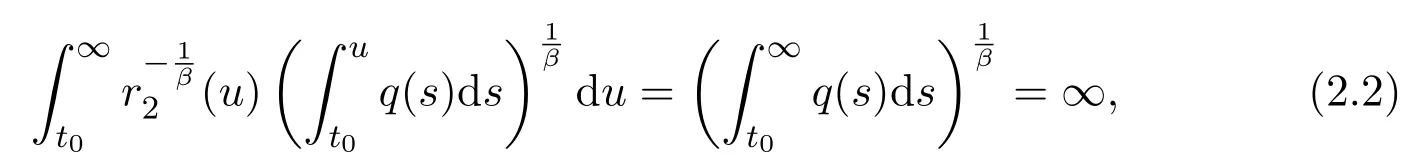
that is,

Now,suppose on the contrary thatyis a nonoscillatory solution of(1.1)on[t0,∞).Without loss of generality,we may assume thatt1≥t0such thaty(t)>0 andy(σ(t))>0 fort≥t1.Using Lemma 2.1,we know thatyeventually belongs to one of the four classes in Lemma 2.1.We will consider each of them separately.
Assumey∈S1.Then fromL1y<0,that is,r1(y′)α<0,we see thaty′<0 andyis decreasing.On the other words,there exists a finite constantℓ≥0 such thatObviously,,too.
We claim thatℓ=0.Assume on the contrary thatℓ>0.Then there exists at2≥t1such thaty(t)≥y(σ(t))≥ℓfort≥t2.Thus,
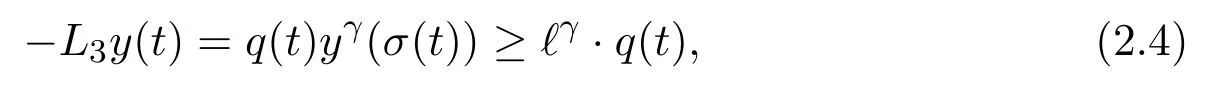
fort≥t2.Integrating(2.4)fromt2tot,we have
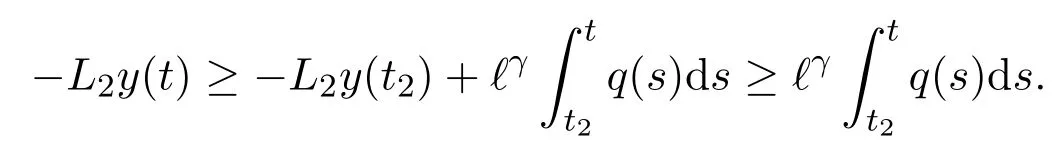
Therefore,
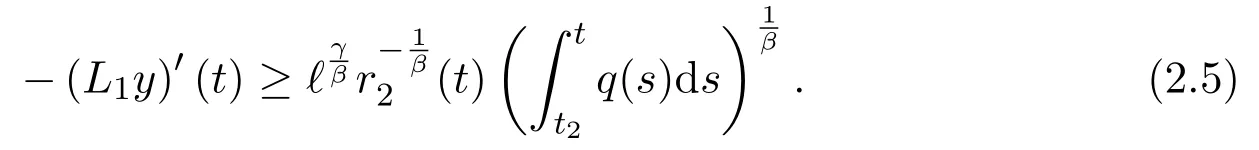
Integrating(2.5)again fromt2tot,we have
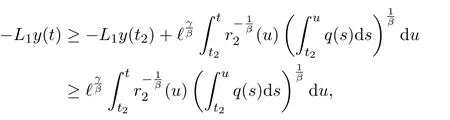
that is,

Integrating(2.6)fromt2tot,and taking account of(2.1),we have
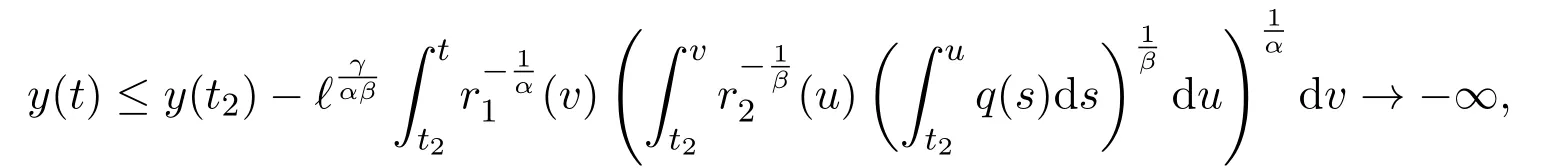
ast→ ∞,which contradicts the positivity ofy.Thus,
Assumey∈S2.Proceeding the same steps as above,we arrive at(2.4).Integrating(2.4)fromt2tot,we have
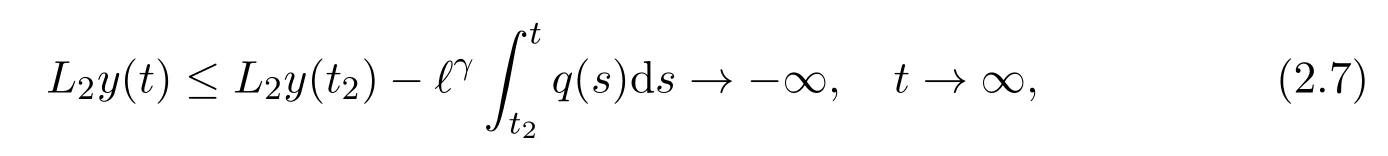
where we used(2.3).This contradicts the positivity ofL2yand thus.
Assumey∈S3.We define a function
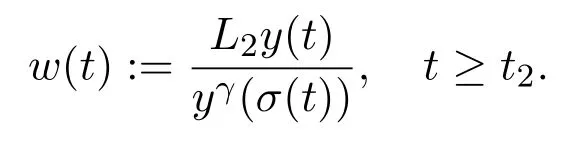
Obviously,w(t)is positive fort≥t2.Using(1.1),we obtain
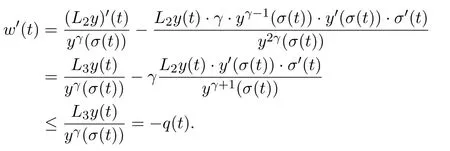
Integrating the above inequality fromt2tot,and taking(2.3)into account,we have
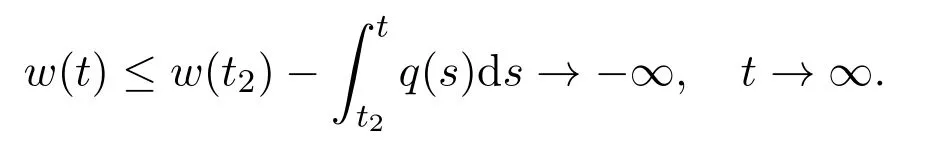
This contradicts the positivity ofw.Hence,S3=Ø.
Assumey∈S4.Considering thatyis increasing,and integrating(1.1)fromt2tot,we obtain
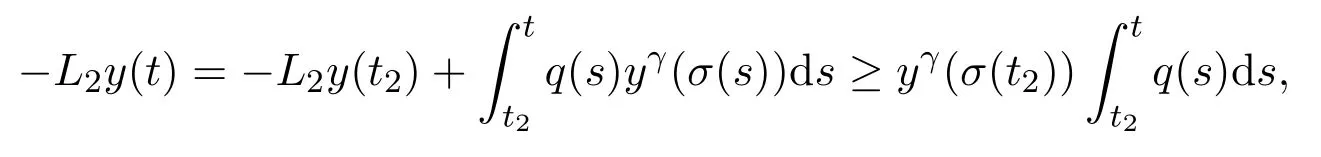
that is,
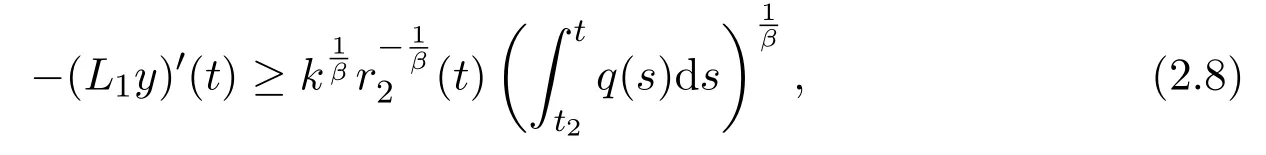
wherek:=yγ(σ(t2)).Integrating(2.8)fromt2totand using(2.2),we have
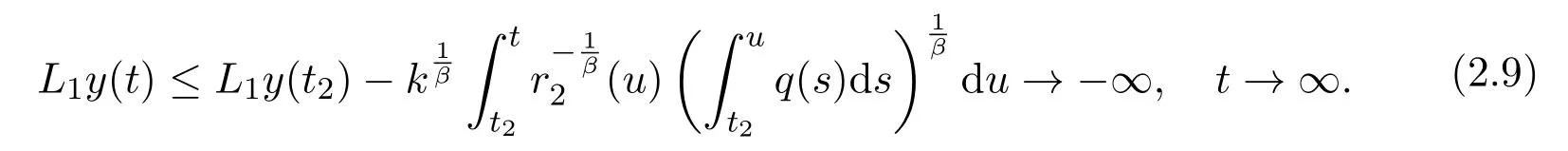
This contradicts the positivity ofL1y.Thus,S4=Ø.The proof is complete.
Remark 2.1It is clear that any nonoscillatory solution in Theorem 2.1 eventually belongs to eitherS1orS2in Lemma 2.1,that is,S3=S4=Ø.
Next,we formulate some additional information about the monotonicity of solutions inS2orS1.
Lemma 2.2Assume(H1)-(H4).Let y∈S2in Lemma2.1on[t1,∞)for some t1≥t0,and define a function
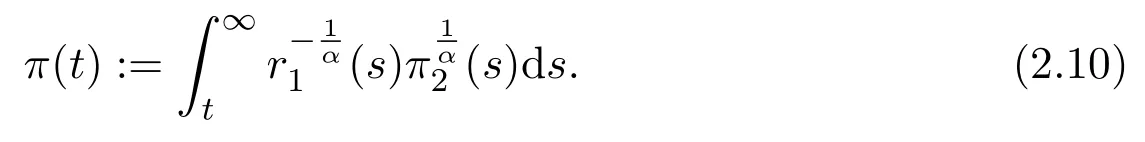
If
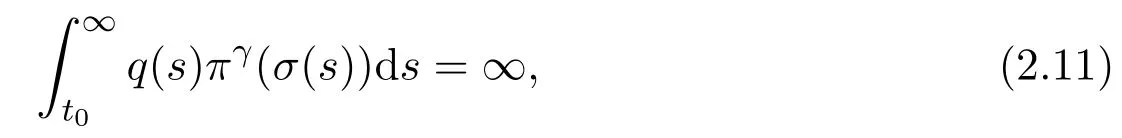
then there exists a t2≥t1such that

for t≥t2.
ProofLety∈S2in Lemma 2.1 on[t1,∞)for somet1≥t0.First,we prove that(2.11)implies

Using I’Hospital rule,we obtain
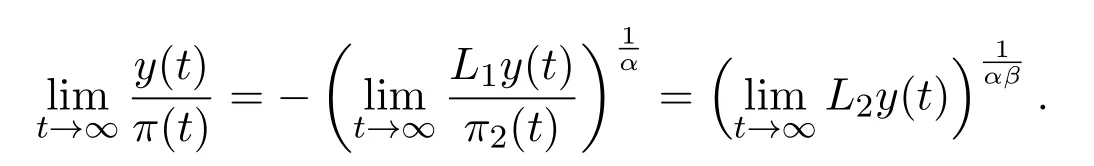
Taking the decrease ofL2y(t)into account,there exists a finite constantℓ≥0 such thatWe claim thatℓ=0.If not,thenL2y(t)≥ℓ>0,andeventually,fort≥t2andt2∈[t1,∞).Using this relation in(1.1),we obtain

Integrating the above inequality fromt2tot,we have
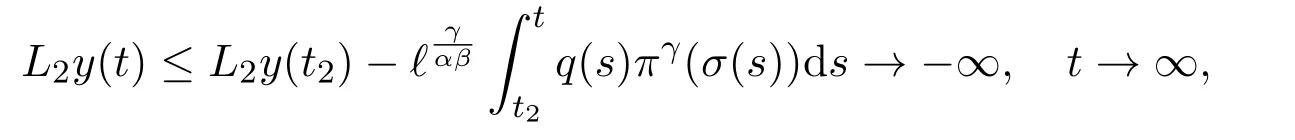
which is a contradiction.Thus(2.13)holds and consequently,also
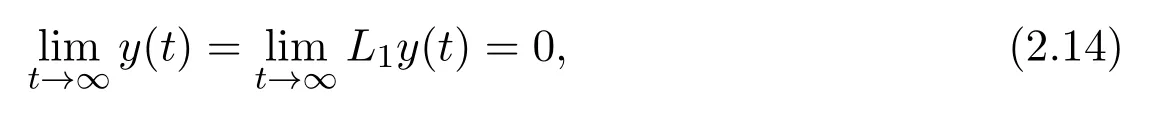
due to the decreasing properties ofπ(t)andπ2(t),respectively.Considering the monotonicity ofL2ytogether with(2.14)yields
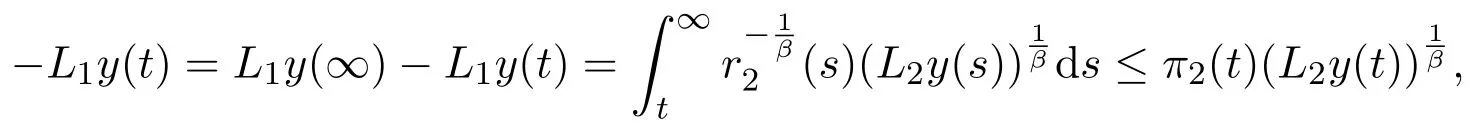
hence,there exists at3≥t2such that
Therefore,there exists at4≥t3such that
and we conclude thaty/πis decreasing on[t4,∞).Hence,(2.12)holds.The proof is complete.
Corollary 2.1Assume(H1)-(H4).Let y∈S2in Lemma2.1on[t1,∞)for some t1≥t0,and a function π(t)be defined by(2.10).If(2.11)holds,then there exists a t2≥t1such that

for every constant k>0and t≥t2.
Lemma 2.3Assume(H1)-(H4).Let y∈S1in Lemma2.1on[t1,∞)for some t1≥t0.If(2.11)holds,then there exists a t2≥t1such that

for t≥t2.
ProofLety∈S1in Lemma 2.1 on[t1,∞)for somet1≥t0.It follows from the monotonicity ofL1ythat,forℓ≥t,
Lettingℓto∞,we have

From(2.17),we conclude thaty/π1is nondecreasing,since
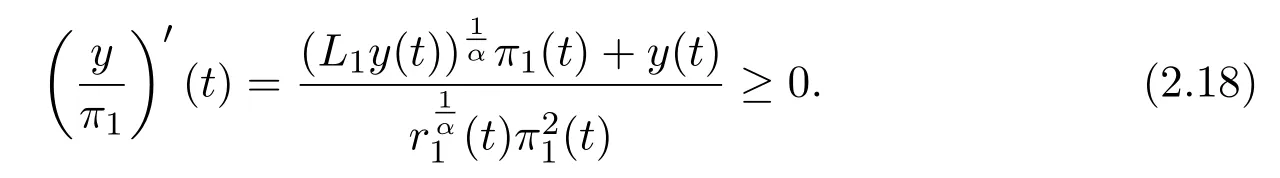
The proof is complete.
Theorem 2.2Assume(H1)-(H4).If
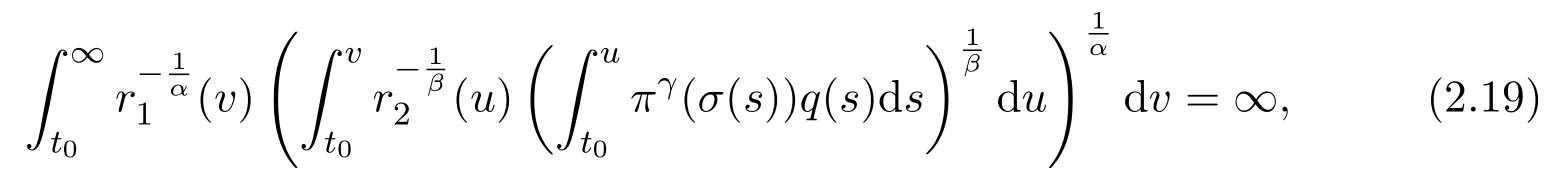
then(1.1)has property A.
ProofSuppose on the contrary and assume thatyis a nonoscillatory solution of(1.1)on[t0,∞).Without loss of generality,we may assume thaty(t)>0 andy(σ(t))>0 fort∈[t1,∞)⊆[t0,∞).Then we obtain thatyeventually belongs to one of the four classes in Lemma 2.1.We will consider each of them separately.
Assumey∈S1.Note that(2.3)and(2.11)are necessary for(2.19)to be valid.In fact,since the functiondsis unbounded due to(H2)andπ′<0,(2.3)and(2.11)must hold.Furthermore,by(2.19),we see that(2.1)holds,and we also obtain
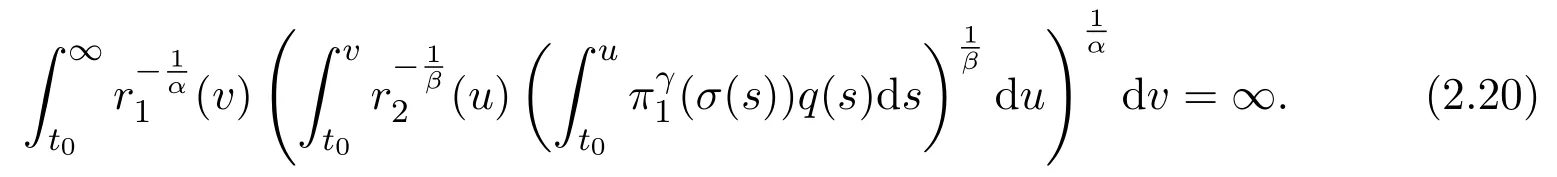
Then using Lemma 2.3,it follows from(2.16)that there existc>0 andt2≥t1such thaty(t)≥cπ1(t)fort≥t2.Substituting this inequality into(1.1),we obtain
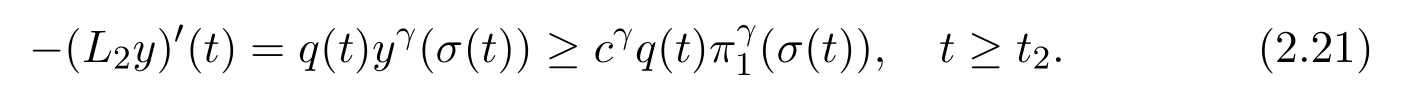
Integrating(2.21)fromt2tot,we have
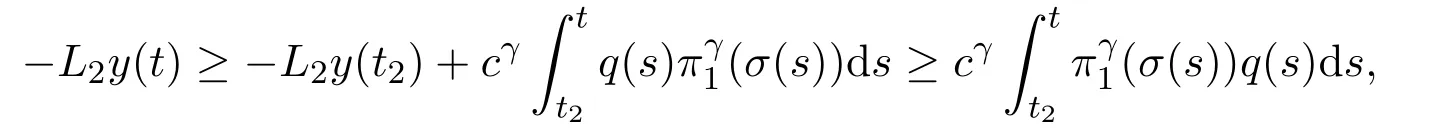
that is,
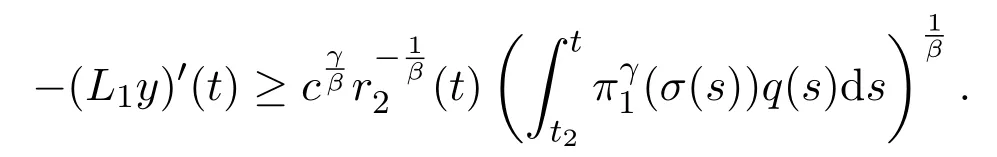
Integrating the above inequality fromt2tot,we have
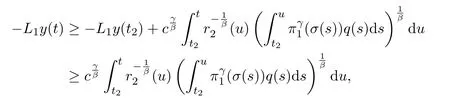
that is,
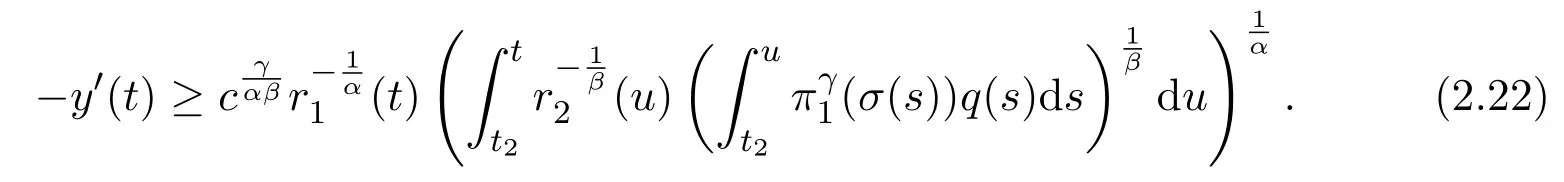
Integrating(2.22)fromt2tot,and taking(2.20)into account,we have
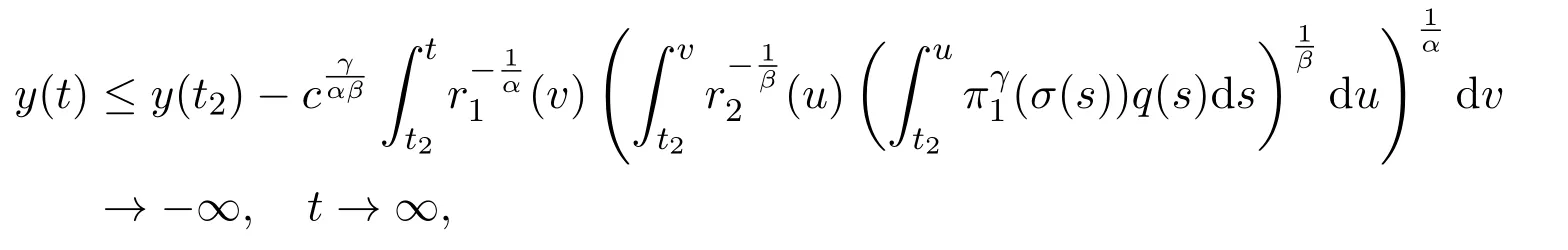
which contradicts the positivity ofy.Thus,S1=Ø.
Assumey∈S2.Noting(2.1)is necessary for the validity of(2.20),we have.
Finally,noting(2.3)and(2.2)are necessary for the validity of(2.19),it follows immediately from Remark 2.1 thatS3=S4=Ø.The proof is complete.
Theorem 2.3Assume(H1)-(H4).If
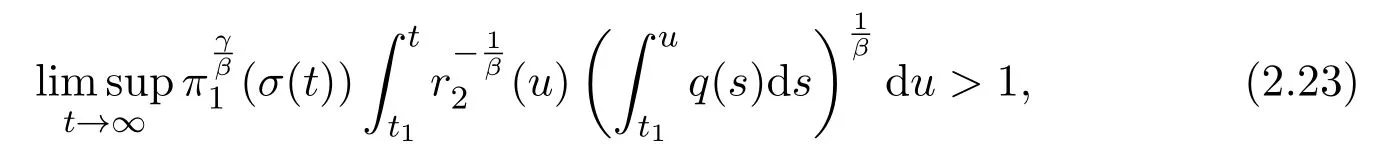
for any t1≥t0,and γ=αβ,then(1.1)has property A.
ProofOn the contrary,suppose thatyis a nonoscillatory solution of(1.1)on[t0,∞).Without loss of generality,we may assume thaty(t)>0 andy(σ(t))>0 fort∈[t1,∞)⊆[t0,∞).Then we obtain thatyeventually belongs to one of the four classes in Lemma 2.1.We will consider each of them separately.
First,note that(2.23)along with(H2)implies(2.3)and(2.2).Then,using Theorem 2.1,we getS3=S4=Ø.Moreover,ify∈S2,then.
Next,we consider the classS1.Assumey∈S1.Integrating(1.1)fromt1totand using the decrease ofy,we have
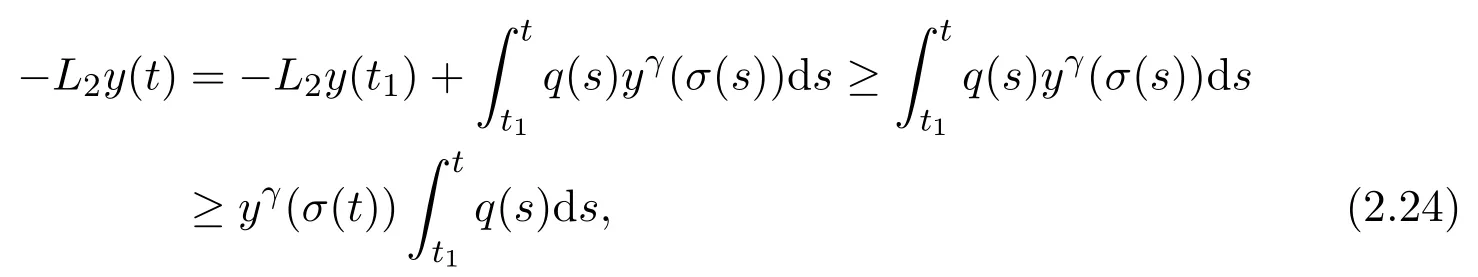
that is,
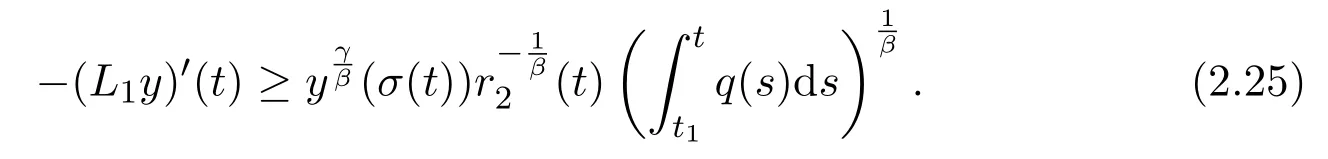
Integrating the above inequality fromt1tot,we have
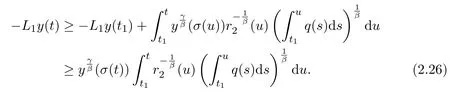
Similar to the proof of Lemma 2.3,we obtain(2.17),which along with(2.26)leads to
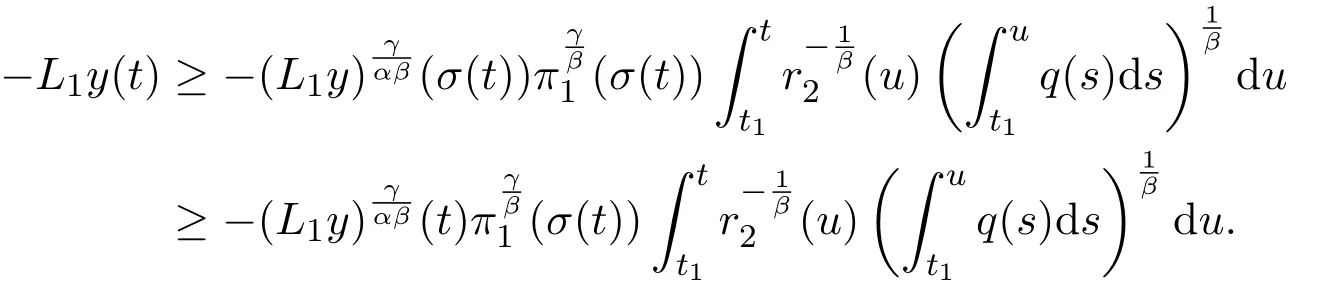
Takingγ=αβinto account,the above inequality becomes
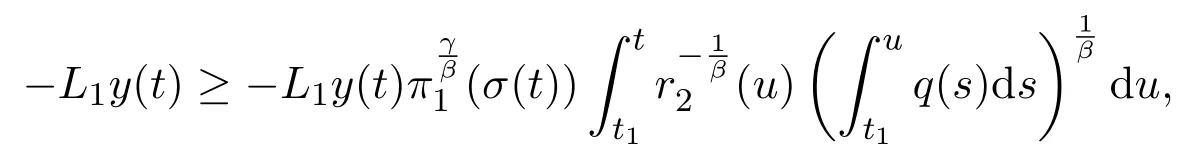
which results in a contradiction
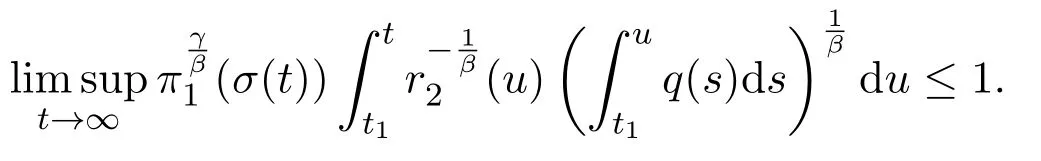
Thus,S1=Ø.The proof is complete.
Theorem 2.4Assume(H1)-(H4)and suppose that(2.1)holds.If
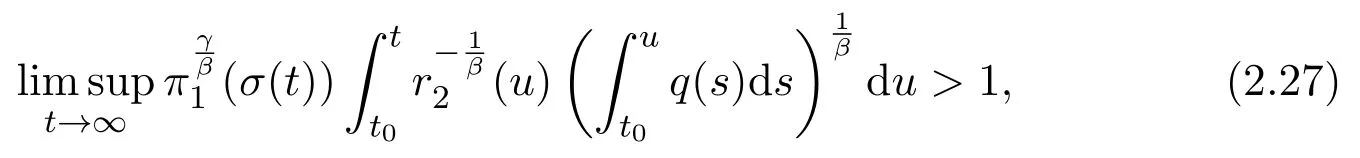
and γ=αβ,then(1.1)has property A.
ProofUsing Theorem 2.1,we haveS3=S4=Ø,and ify∈S2,then.
Now,we only need to consider the classS1.Assumey∈S1.Similar to the proof of Theorem 2.3,we arrive at

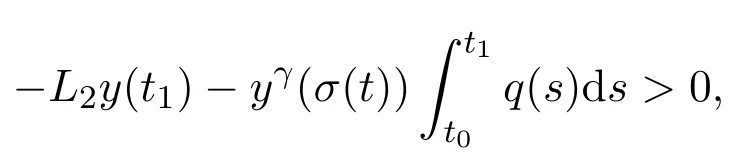
fort≥t2.Thus,fort≥t2,we have
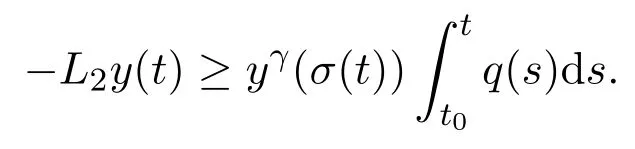
Integrating the above inequality fromt2tot,we have
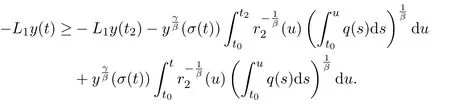
There also exists at3>t2such that
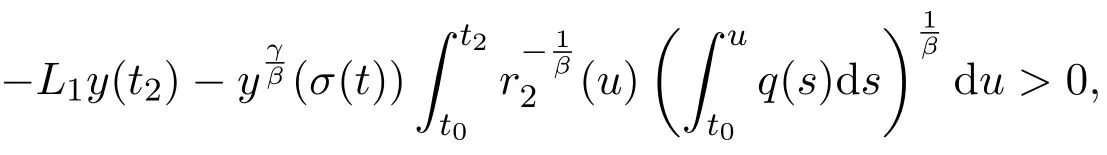
fort≥t3.Thus,fort≥t3,we obtain
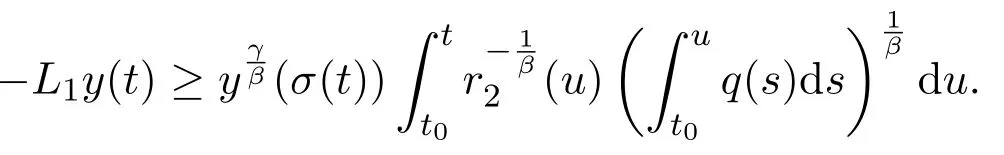
The rest of proof is similar and hence we omit it.Finally,we obtainS1=Ø.The proof is complete.
Next,we will establish various oscillation criteria for(1.1).
Theorem 2.5Assume(H1)-(H4).If
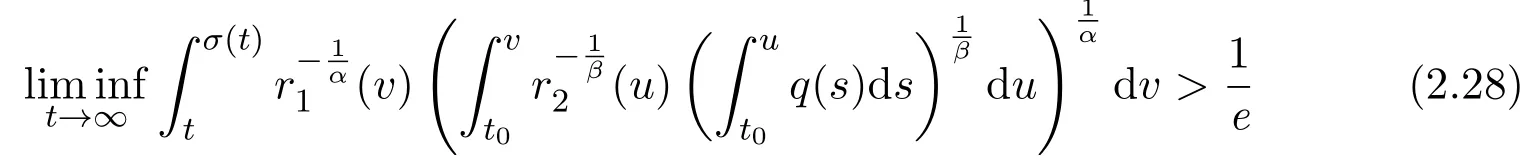
and
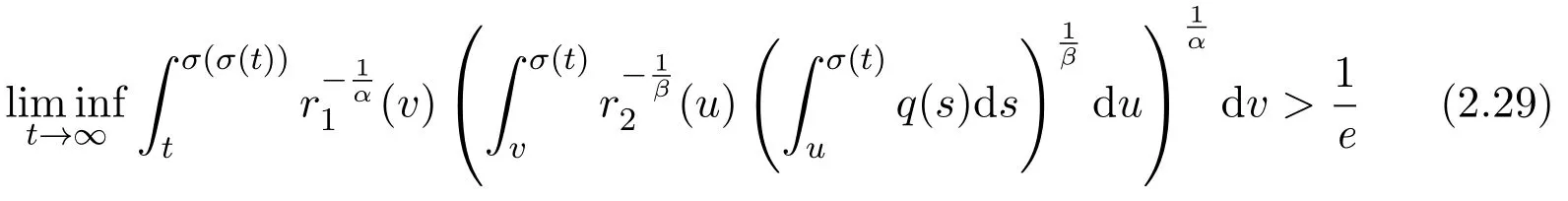
hold,and moreover,αβ=γ,then(1.1)is oscillatory.
ProofSuppose thatyis a nonoscillatory solution of(1.1)on[t0,∞).Without loss of generality,we may assume thatt1≥t0such thaty(t)>0 andy(σ(t))>0 fort≥t1.Then we obtain thatyeventually belongs to one of the four classes in Lemma 2.1.In following,we consider each of these classes separately.
Assumey∈S1.Similar to the proof of Theorem 2.3,we arrive at(2.26),that is

Usingαβ=γ,the above inequality becomes
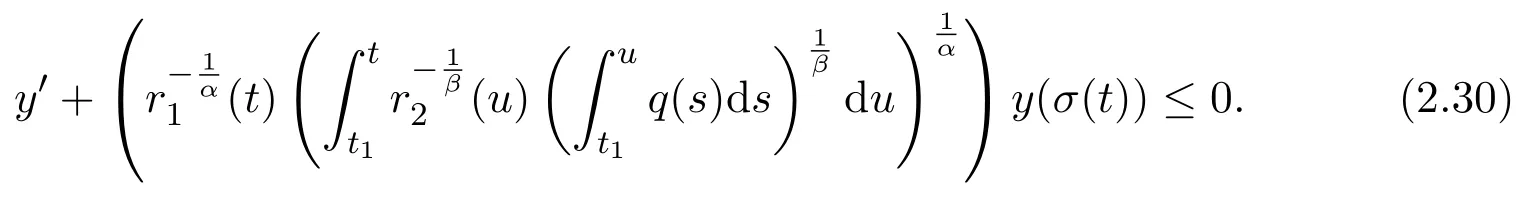
However,it is well-known(see,e.g.,[5,Theorem 2.4.1])that condition(2.28)implies the oscillation of(2.30).Thus,it contradicts our initial assumption.ThenS1=Ø.
Assumey∈S2.Integrating(1.1)fromttou(t that is, Integrating the above inequality fromttou,we have that is, Takingγ=αβinto account,we have Settingu=σ(t)in(2.31),we get that is, However,condition(2.29)implies the oscillation of(2.32),(see,e.g.,[5,Theorem 2.4.1]).It means that(1.1)cannot have a positive solutionyin the classS2,which is a contradiction.Thus,S2=Ø. Finally,noting that(2.1)is necessary for the validity of(2.28),it follows immediately from Remark 2.1 thatS3=S4=Ø.The proof is complete. The following results are simple consequences of the above theorem and Corollary 2.1. Theorem 2.6Assume(H1)-(H4).If γ=αβ,(2.11)and(2.28)hold,then all positive solutions of(1.1)satisfy(2.15)for any k>0and t large enough. Theorem 2.7Assume(H1)-(H4).If γ=αβ,(2.19)and(2.29)hold,then(1.1)is oscillatory. Remark 2.2If holds,we have the validity of(2.29).Thus,the conclusions of Theorems 2.5 and 2.7 remain valid if condition(2.29)is replaced by(2.33). Theorem 2.8Assume(H1)-(H4).If γ=αβ,(2.23)and(2.33)hold,then(1.1)is oscillatory. Theorem 2.9Assume(H1)-(H4).If γ=αβ,(2.1),(2.27)and(2.33)hold,then(1.1)is oscillatory. In order to prove the following conclusions,we recall an auxiliary result which is taken from Wu et al.[6,Lemma2.3]. Lemma 2.4[6,Lemma2.3]Let,where B>0,A andC are constants,and α is a quotient of odd positive numbers.Then g attains itsmaximum value onRatand for t≥t2. Theorem 2.10Assume(H1)-(H4)and γ=αβ.If(2.3)and(2.33)hold,and also there exists a function ρ∈C1([t0,∞),(0,∞))such that for any T∈[t0,∞),then(1.1)is oscillatory. ProofOn the contrary,suppose thatyis a nonoscillatory solution of(1.1)on[t0,∞).Without loss of generality,we may assume thaty(t)>0 andy(σ(t))>0 fort∈[t1,∞)⊆[t0,∞).Then we know thatyeventually belongs to one of the four classes in Lemma 2.1.We will consider each of them separately. Assumey∈S1.Define the generalized Riccati substitution Taking(2.17)into account,we see thatw≥0 on[t1,∞).Differentiating(2.36),we arrive at Similar to the proof of Theorem 2.3,we arrive at(2.25).Using(2.16)in(2.25),we deduce that the inequality holds fort≥t2,wheret2∈[t1,∞)is large enough.Considering(2.37)and(2.38),it follows that Let Using(2.34)with the above inequality,we have Integrating(2.39)fromt2tot,we obtain Taking the definition ofwinto account,we get On the other hand,using(2.17),it follows that Substituting the above estimate into(2.40),we get Multiplying(2.41)byand taking the limsup on both sides of the resulting inequality,we obtain a contradiction with(2.35).Thus,S1=Ø. Assumey∈S2.Similar to the proof of Theorem 2.5,one arrives at a contradiction with(2.33).Thus,S2=Ø. In following,we showS3=S4=Ø.Since(2.3)holds due to(H2),then the function is unbounded,and so(2.2)holds.The rest of proof proceeds in the same manner as that of Theorem 2.1.The proof is complete. Depending on the appropriate choice of the functionρ,we can use Theorem 2.10 in a wide range of applications for studying the oscillation of(1.1).Thus,by choosing,ρ(t)=π1(t)andρ(t)=1,we obtain the following results,respectively. Corollary 2.2Assume(H1)-(H4)and γ=αβ.Moreover,assume that(2.3)and(2.33)hold.If for any T∈[t0,∞),then(1.1)is oscillatory. Corollary 2.3Assume(H1)-(H4)and γ=αβ.Moreover,assume that(2.3)and(2.33)hold.If for any T∈[t0,∞),then(1.1)is oscillatory. Corollary 2.4Assume(H1)-(H4)and γ=αβ.Moreover,assume that(2.3)and(2.33)hold.If for any T∈[t0,∞),then(1.1)is oscillatory. Remark 2.3The conclusions of Theorem 2.10 and Corollaries 2.2-2.4 remain valid if condition(2.3)is replaced by(2.1). Lemma 2.5Assume(H1)-(H4)and γ=αβ.Furthermore,assume that(2.1)holds.Suppose that(1.1)has a positive solution y∈S1on[t1,∞)⊆[t0,∞)and that λ andµare constants satisfying and Then there exists a t∗∈[t1,∞)such that and on[t∗,∞). ProofAssumey∈S1.Similar to the proof of Theorem 2.3,we arrive at(2.25).Considering(1.1),(2.17)and(2.37),we see that It is easy to verify that and thus,we get Therefore, Next,we will prove the last monotonicity.Similar to the proof of Theorem 2.3,we arrive at(2.26),that is Using(2.16)with the above inequality,we have that is, fort≥t2,wheret2≥t1.Using the above relation in the equality and taking the condition(2.47)into account,we get Theorem 2.11Assume(H1)-(H4)and γ=αβ.Furthermore,suppose that(2.33)holds and λ andµare constants satisfying(2.45)-(2.47).If for any t1≥t0,then(1.1)is oscillatory. Proof Suppose on the contrary thatyis a nonoscillatory solution of(1.1)on[t0,∞).Without loss of generality,we may assume thaty(t)>0 andy(σ(t))>0 fort∈[t1,∞)⊆[t0,∞).Then we know thatyeventually belongs to one of the four classes in Lemma 2.1.We will consider each of them separately. Before proceeding further,note that(2.11)and are necessary for(2.19)to be valid.To verify this,it suffices to see that(H2)implies From the above inequality,we conclude that the function and consequently must be unbounded. Assumey∈S1.Similar to the proof of Theorem 2.3,we arrive at(2.26),that is Using the conclusions of Lemma 2.5 thatis nonincreasing andis nondecreasing,we obtain Using(2.52)in the above inequality,we have that is, Taking the limsup on both sides of the above inequality,we reach a contradiction with(2.53).Thus,S1=Ø. Accounting to Remark 2.2 with(2.33),we haveS2=Ø.Also,using Theorem 2.1,we arrive atS3=S4=Ø.The proof is complete. Theorem 2.12Assume(H1)-(H4)and γ=αβ.Furthermore,suppose that(2.3)and(2.33)hold,and λ∈[0,α)is a constant satisfying(2.46).If there exists a function ρ∈C1([t0,∞),(0,∞))and T∈[t0,∞)such that then(1.1)is oscillatory. ProofFor the proof of this theorem,it suffices to use(2.48)instead of(2.16)in(2.25)in the proof of Theorem 2.10. Corollary 2.5Assume(H1)-(H4)and γ=αβ.Furthermore,suppose that(2.3)and(2.33)hold and λ∈[0,α)is a constant satisfying(2.46).If for any T∈[t0,∞),then(1.1)is oscillatory. In this section,we illustrate the strength of our results using two Euler-type differential equations,as two examples. Example 3.1Consider the third-order advanced differential equation It is easy to verify that condition(2.1)is satisfied.Using Theorem 2.1,we obtain that equation(3.1)has property A. Example 3.2Consider the third-order advanced differential equation wherem>1,,q0>0 andδ≥1 . Clearly,r1(t)=tm,r2(t)=tn,α=1,,σ(t)=δt,and From Theorem 2.1(On the asymptotic properties of nonoscillatory solutions),it is easy to verify that condition(2.1)holds.Thus,any nonoscillatory,say positive solution of equation(3.2)converges to zero ast→∞,without any additional requirement. In following,we consider the oscillation of equation(3.2). After some computations,we note that conditions(2.23),(2.28)and(2.33)reduce to and respectively. Theorem 2.5 and Remark 2.2 imply if both(3.4)and(3.5)hold,then equation(3.2)is oscillatory. Since condition(2.19)is not satisfied,the related result from Theorem 2.7 can not be applied. Theorems 2.8 and 2.9 can deduce that oscillation of equation(3.2)is guaranteed by conditions(3.3)and(3.5). In this paper,we studied the third-order differential equation(1.1)with noncanonical operators.First,we established one-condition criteria for property A of(1.1).Next,we presented various two-condition criteria ensuring oscillation of all solutions of(1.1).Finally,our results are applicable on Euler-type equations of the forms(3.1)and(3.2).It remains open how to generalize these results for higher-order noncanonical equations with deviating arguments. Acknowledgements The authors would like to express their highly appreciation to the editors and the referees for their valuable comments.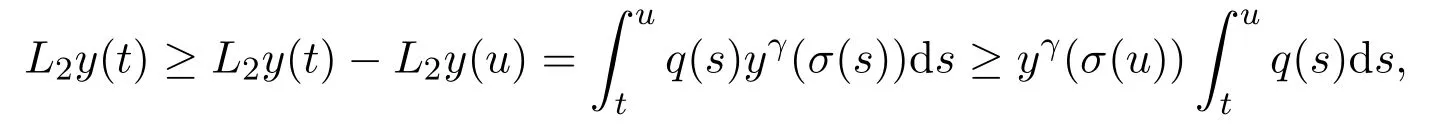
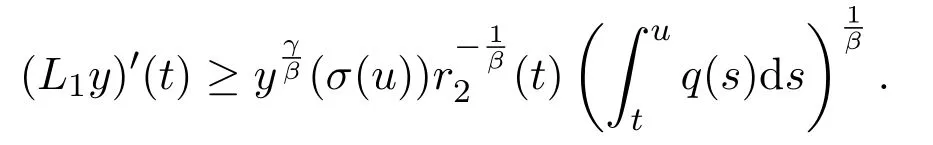
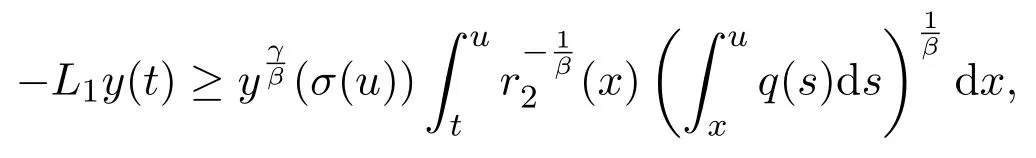

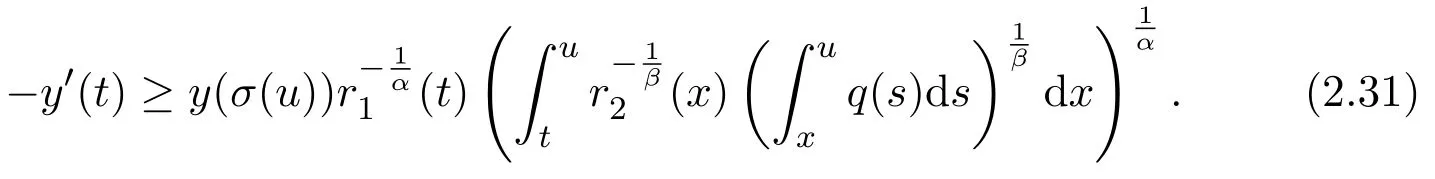
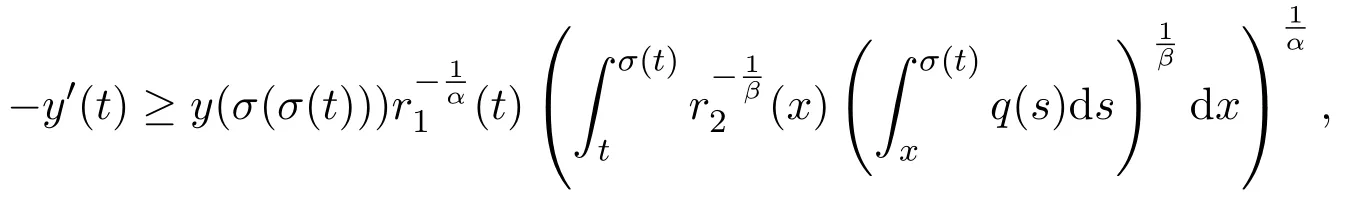
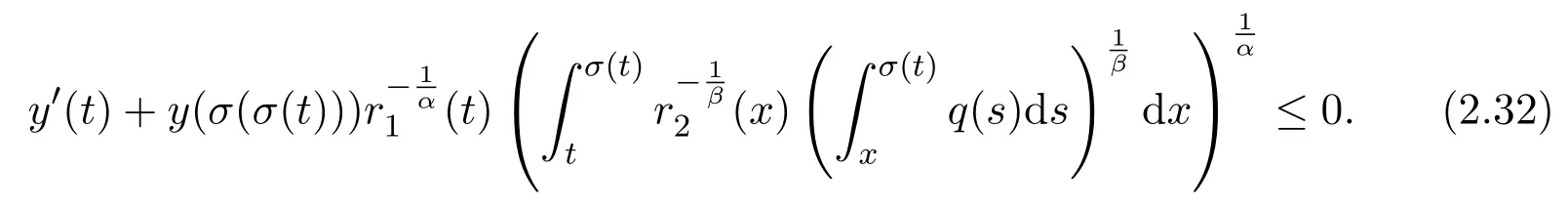

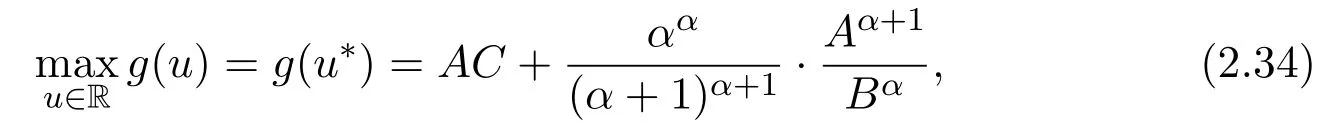

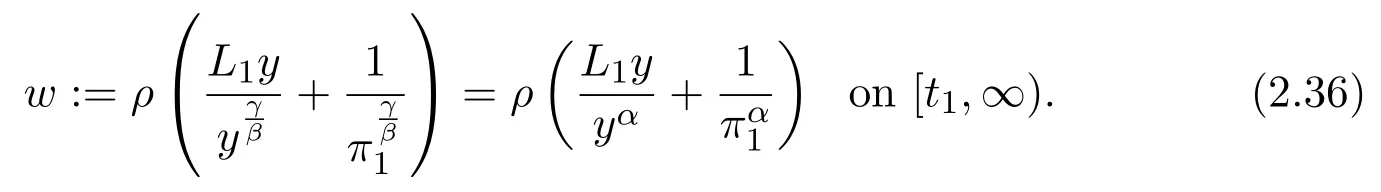
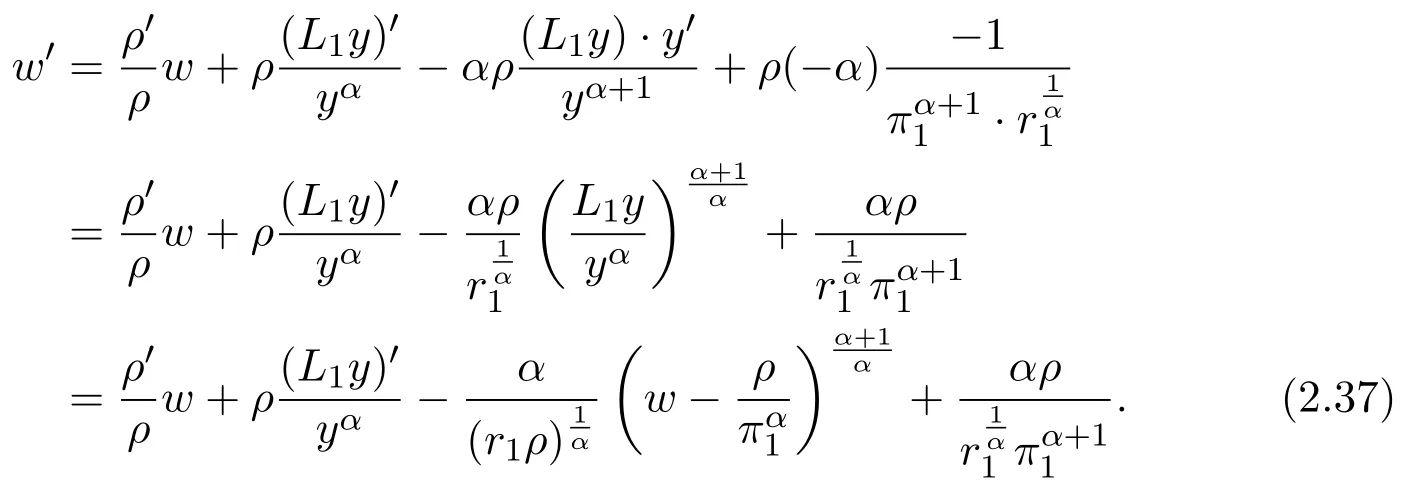
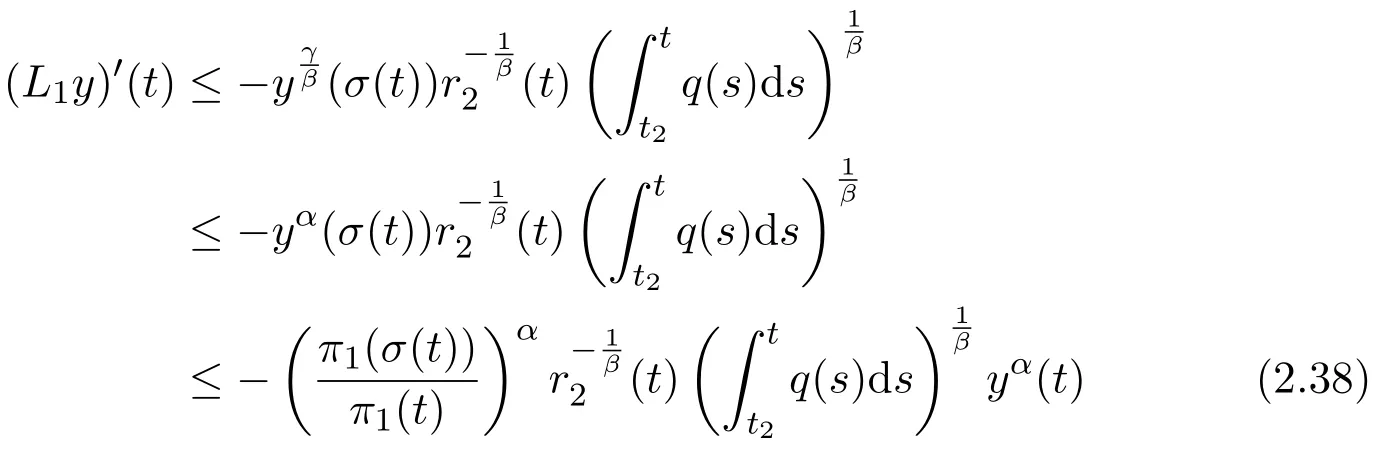


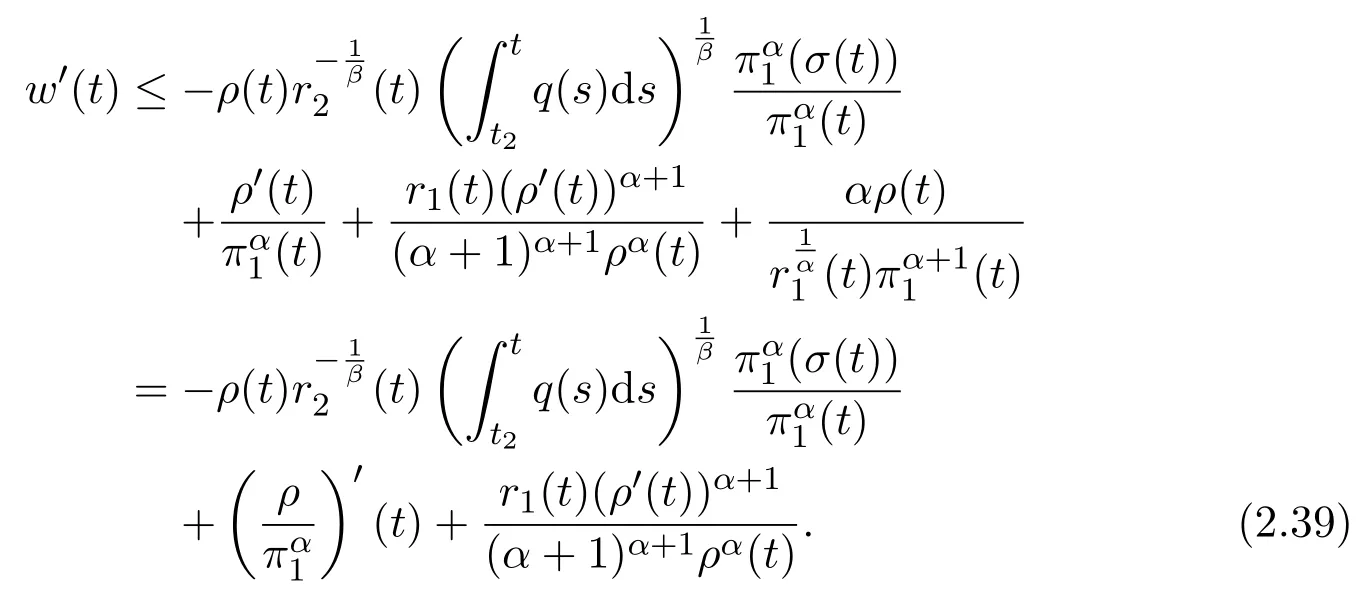
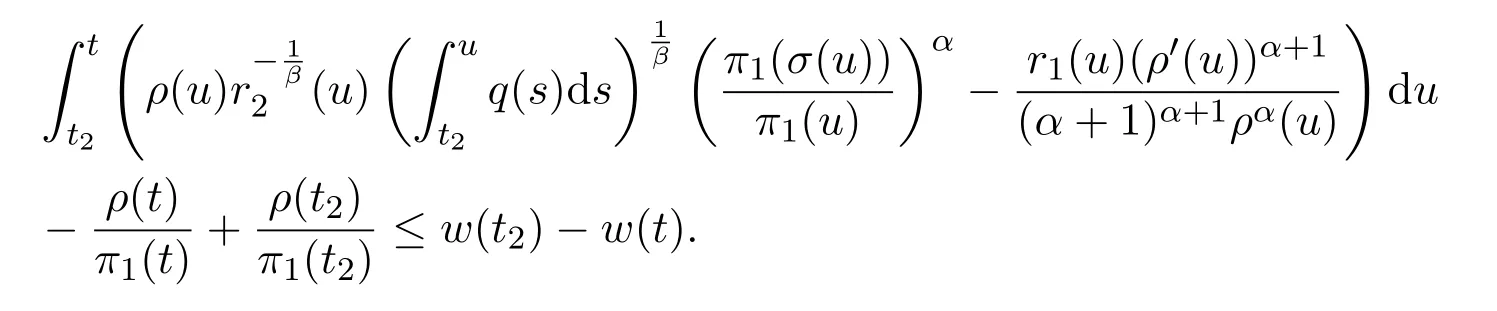

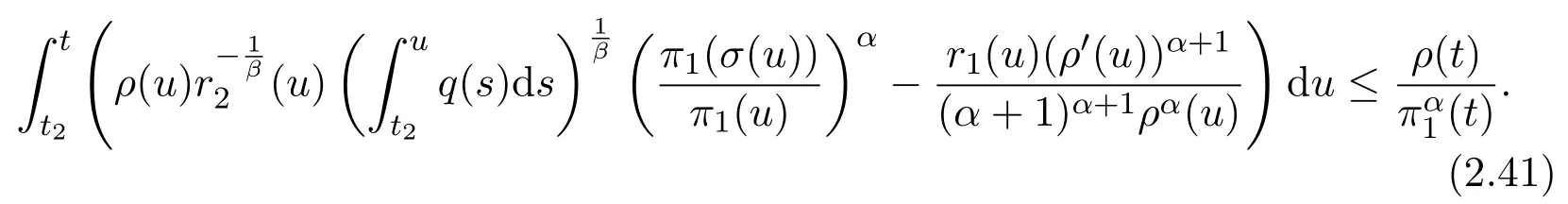
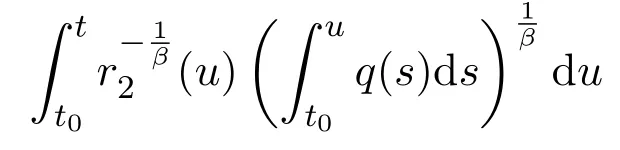
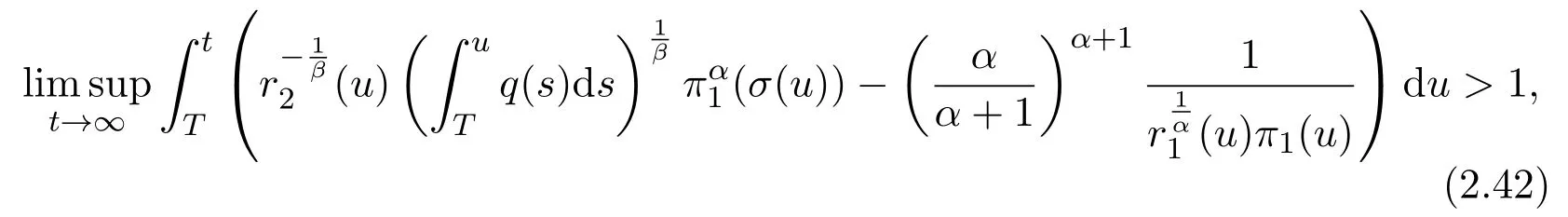
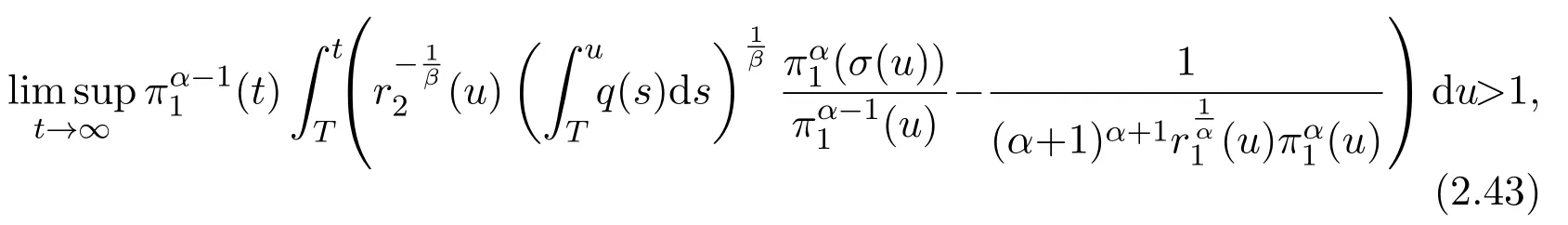
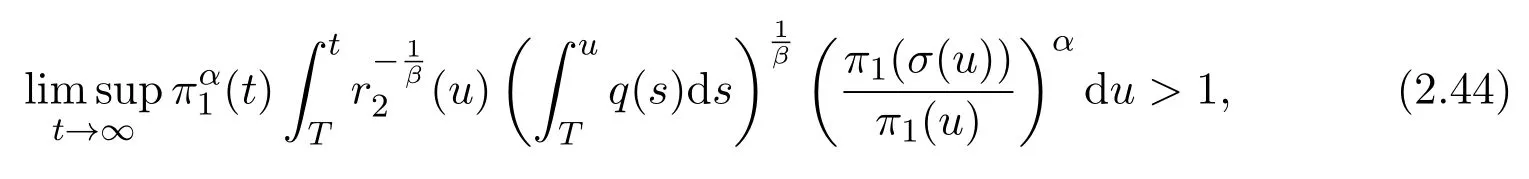

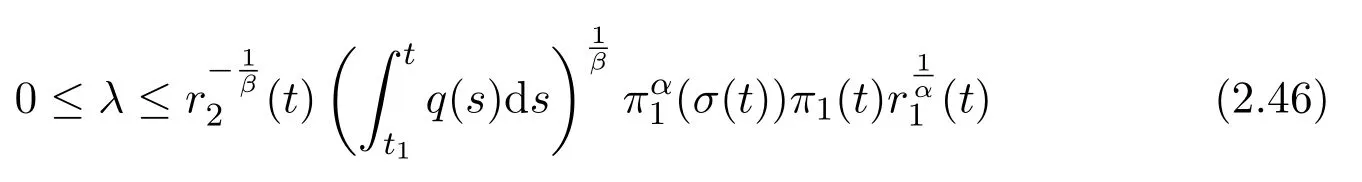
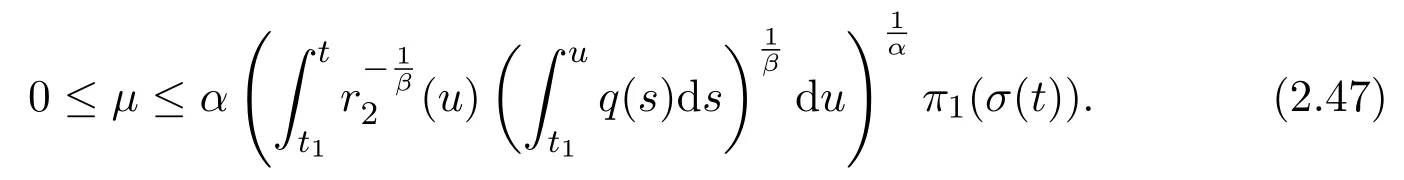


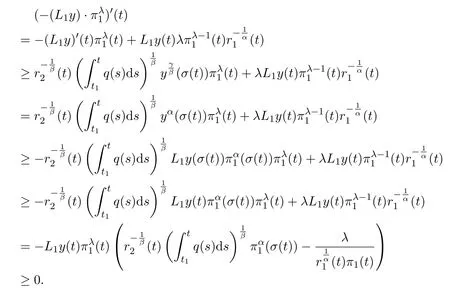
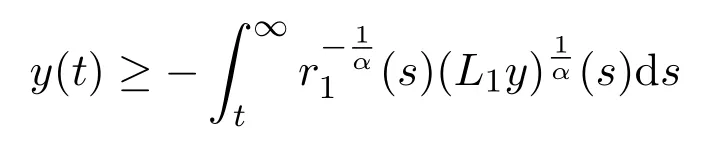

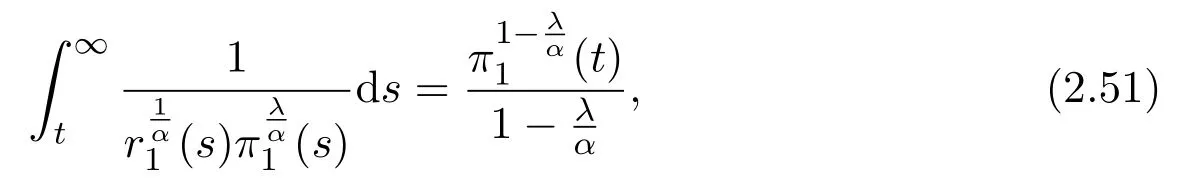
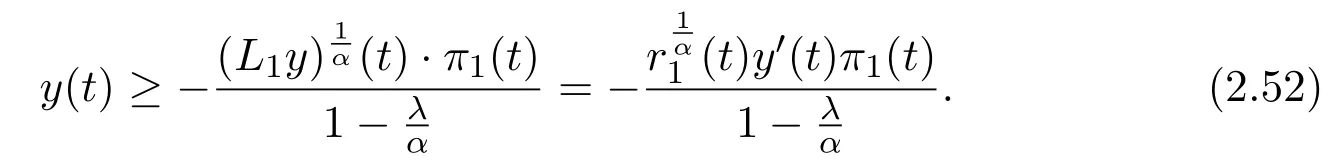
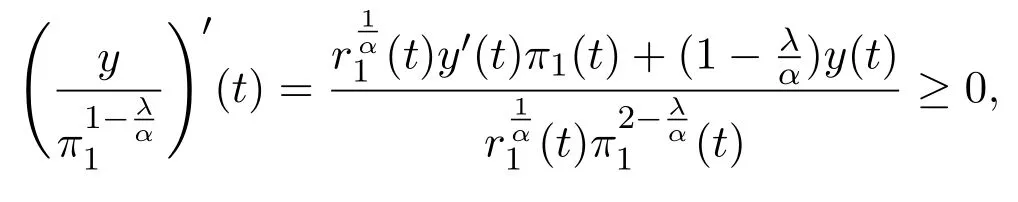
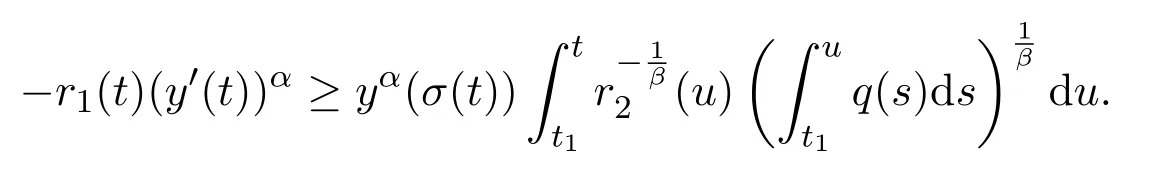
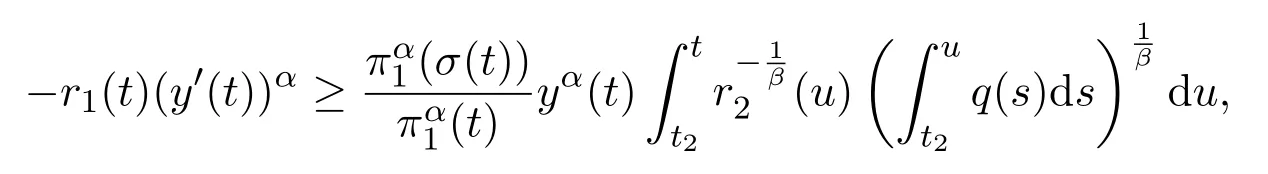
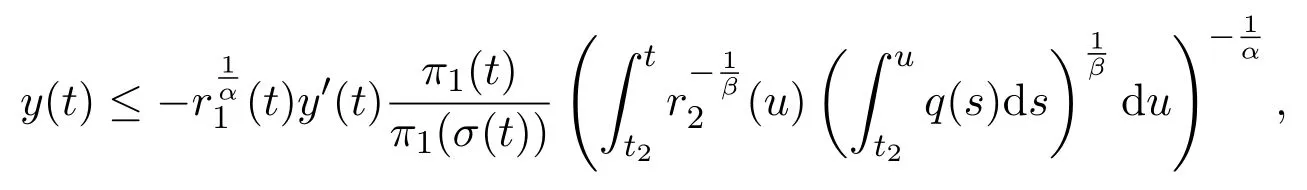
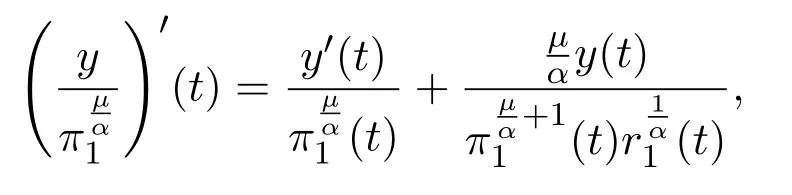
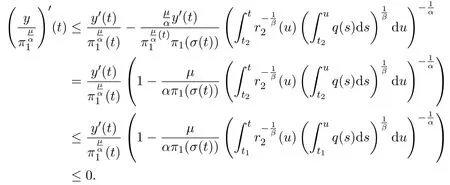
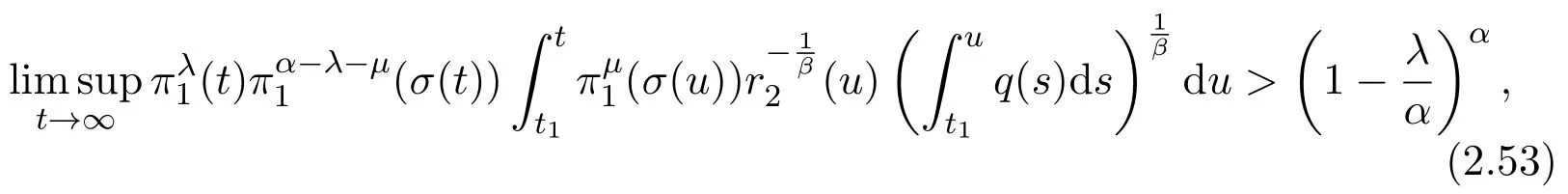
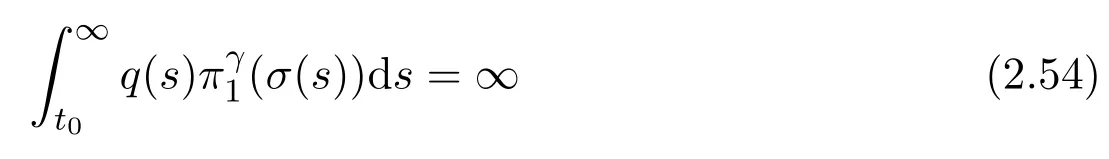
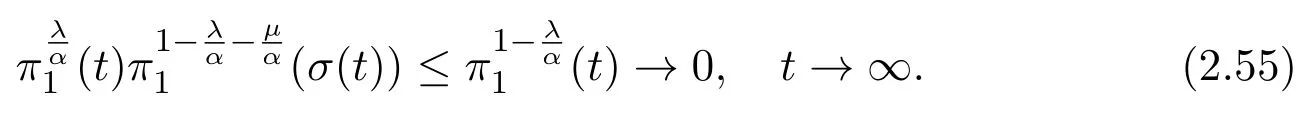
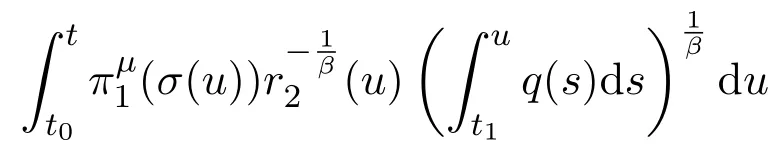
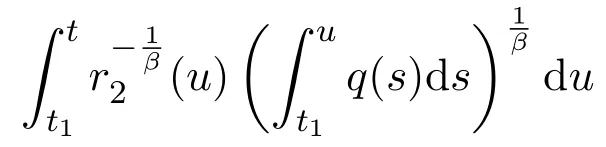



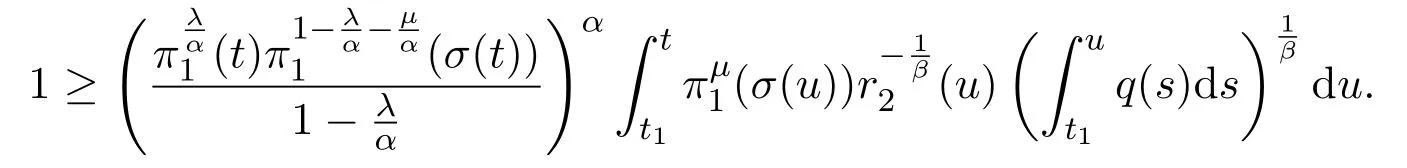
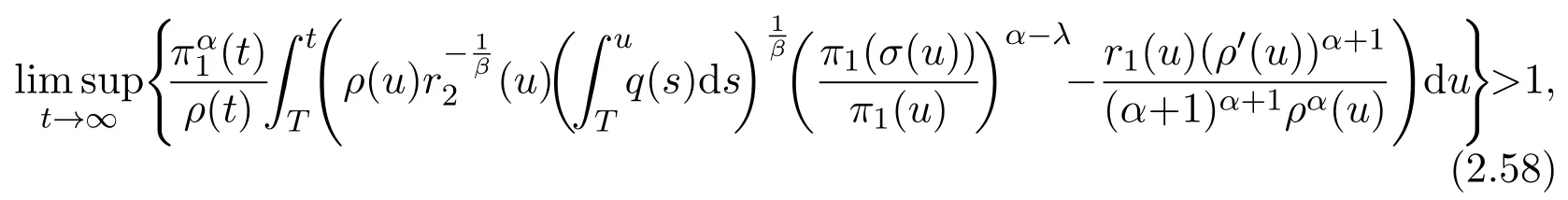
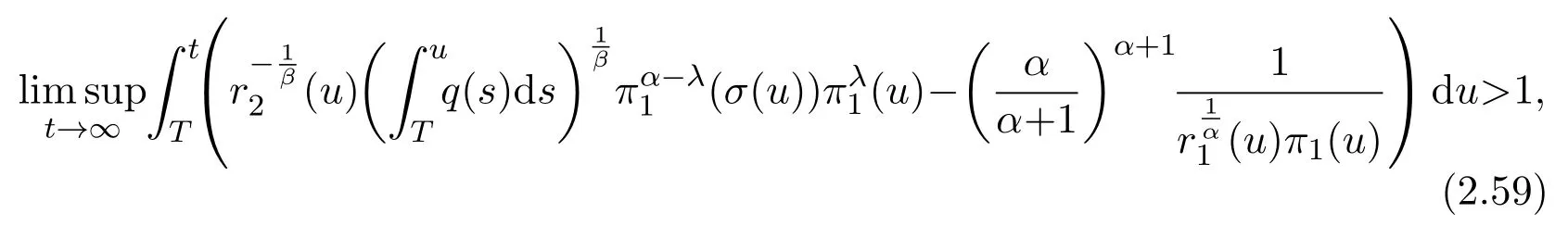
3 Examples
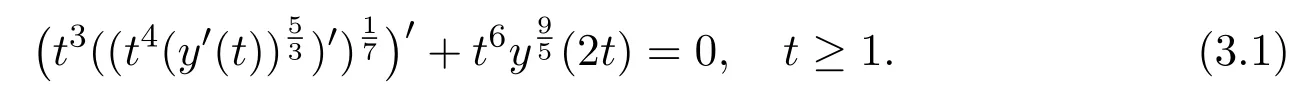

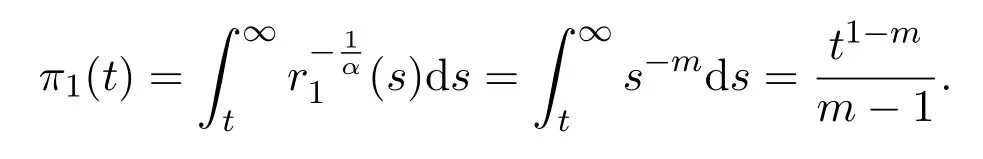
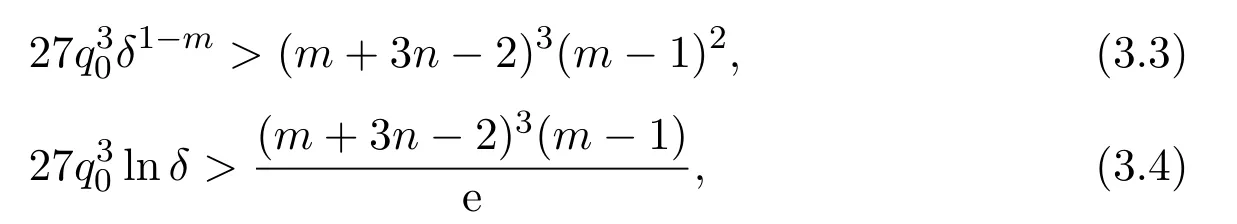
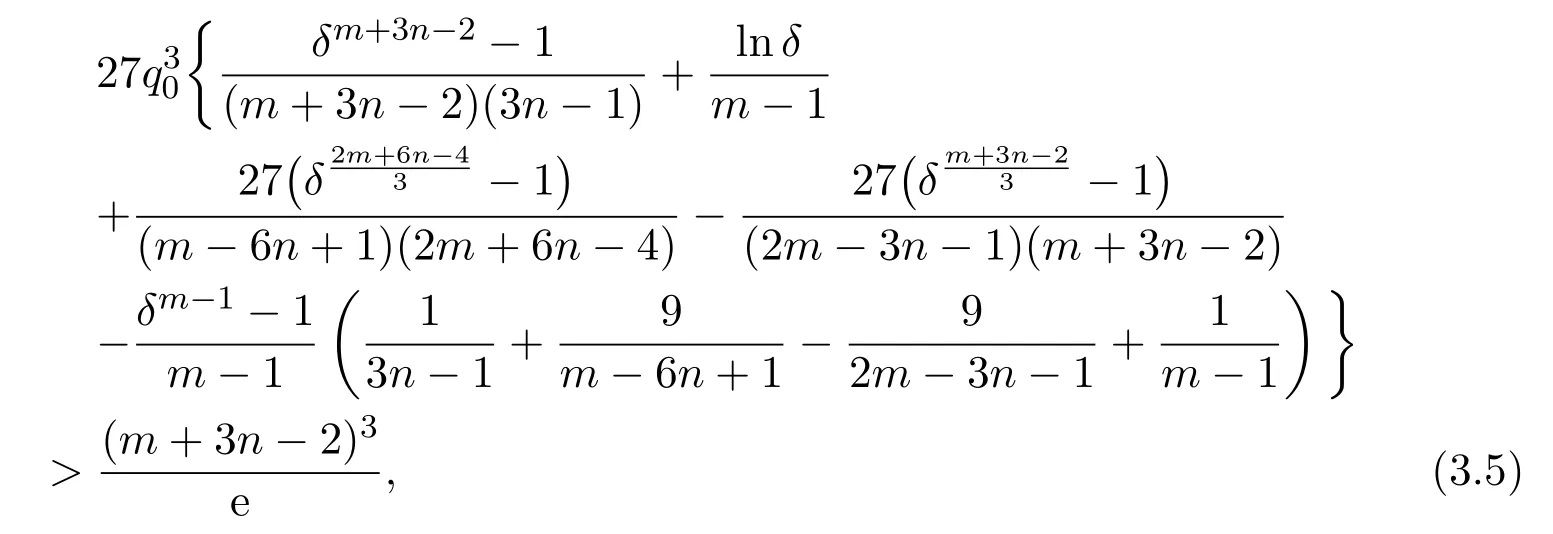
4 Summary
杂志排行
Annals of Applied Mathematics的其它文章
- TRAVELING WAVE SOLUTIONS FOR A PREDATOR-PREY MODEL WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE∗†
- THE EFFECT OF REFUGE AND PROPORTIONAL HARVESTING FOR A PREDATOR-PREY SYSTEM WITH REACTION-DIFFUSION∗†
- POSITIVE SOLUTIONS TO A BVP WITH TWO INTEGRAL BOUNDARY CONDITIONS∗†
- UNSTEADY NATURAL CONVECTIVE BOUNDARY LAYER FLOW AND HEAT TRANSFER OF FRACTIONAL SECOND-GRADE NANOFLUIDS WITH DIFFERENT PARTICLE SHAPES∗†
- BICYCLIC GRAPHS WITH UNICYCLIC OR BICYCLIC INVERSES∗†
- BIFURCATION ANALYSIS OF A CLASS OF PLANAR PIECEWISE SMOOTH LINEAR-QUADRATIC SYSTEM∗†
