UNSTEADY NATURAL CONVECTIVE BOUNDARY LAYER FLOW AND HEAT TRANSFER OF FRACTIONAL SECOND-GRADE NANOFLUIDS WITH DIFFERENT PARTICLE SHAPES∗†
2020-09-14MingShenYuhangWuMengchenZhang
Ming Shen,Yuhang Wu,Mengchen Zhang
(College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,Fujian,PR China)
Abstract
Keywords second-grade nanofluid;heat transfer;Caputo derivative;particle shape
1 Introduction
The study of the non-Newtonian fluids has achieved much attention because of well-established applications in a number of processes which occur in industry such as damping and braking devices,personal protective equipment,machining,rocket propellants.The shear stress and shear rate of the non-Newtonian fluids are connected by a relation in a non-linear manner which is generally more complex compared with Newtonian fluid flows.Many research works have been carried out to explore various non-Newtonian fluid flows.Khan et al.[1]studied the heat and mass flux models on three-dimensional flow of Burgers fluid over a stretching surface.The magnetohydrodynamics(MHD)three-dimensional flow of Oldroyd-B nano fluids was discussed by Hayat et al.[2].Ramzan et al.[3]studied on the effect of thermal diffusion on the boundary layer flow of mixed convective viscoelastic nano fluids in a porous medium.Alshomrani et al.[4]researched the heat and mass transfer characteristics of steady-state flow of three-dimensional Burgers nano fluids on biaxially stretched surfaces.Bilal et al.[5]investigated the three-dimensional radiation flow of Burgers nano fluids with mass flux effect.Effect of nonlinear radiation on the flow of MHD Carreau nano fluids on a tensile surface with zero mass flux was analyzed by Lu et al.[6].One of the most popular models for non-Newtonian fluids is the second-grade fluid model which was configured firstly by Coleman and Noll[7].Subsequently,Bose et al.[8]made a study on Couette flow of second-grade fluid through a porous medium with suction.Exact solutions of a second-grade fluid movement owing to cylinder vibration were presented by Vieru et al.[9].Jamil and Fetecau[10]discussed exact analytic solutions of rotating flows of a second-grade fluid between cylindrical regions.
Fractional derivatives are better than integer order models in some applications because they can describe the hereditary and memory properties of diverse substances.For example,complex kinetics can be accurately described,and it can also effectively treat viscoelastic properties.The study of fractional derivative models of non-Newtonian fluids generally begins with classical differential equations,which generally use fractional operators instead of integer-order time derivative.Natural convection flow of a second-grade fluid with non-integer order time-fractional derivatives was studied by Imran et al.[11].With the consideration of Soret and Dufour effects,Zhao et al.[12]introduced the fractional derivative to characterise the natural convection heat and mass transfer of a MHD viscoelastic fluid in a porous medium.Ming et al.[13]derived analytical solutions of a class of new multiterm fractional-order partial differential equations.Rasheed et al.[14]discussed an unsteady flow of an anomalous Oldroyd-B fluid for solving fractional equation.Zhao et al.[15]studied unsteady natural convection heat transfer of generalized Oldroyd-B fluid in a porous medium saturated with modified fractional Darcy’s law.Smooth travelling wave solutions of two fractional flow equations from porous media resulting were analyzed by H¨onig et al.[16].
The second-grade fluid model is one of the non-Newtonian models,but it is rare to analyze its fractional derivative.This work is aimed to study the natural convection flow of an incompressible fractional second-grade nano fluid near a vertical plate with different particle shapes,and introduce Caputo fractional derivatives into the stress tensor component.The expressions for dimensionless velocity and temperature are solved numerically.The influences of flow parameters as well as the fractional derivative parameterαon the velocity and temperature field are analyzed graphically.
2 Mathematical Formulation of the Problem
Consider the two-dimensional unsteady natural convective boundary layer flow and heat conduction of second-grade nano fluids over a vertical plate.In the cartesian coordinate system,thex-axis is along the upward direction of the plate and theyaxis is perpendicular to the plate.The temperature of the vertical plate and the ambient plate areTwandT∞,respectively.
For fractional second-grade fluid model,the stress tensor componentτxycan be described as[17]
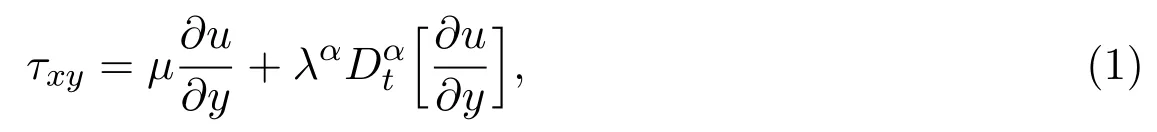
whereµis the effective viscosity,λis relaxation time,is the Caputo fractional derivative and the fractional derivative of orderαis de fined as[18]
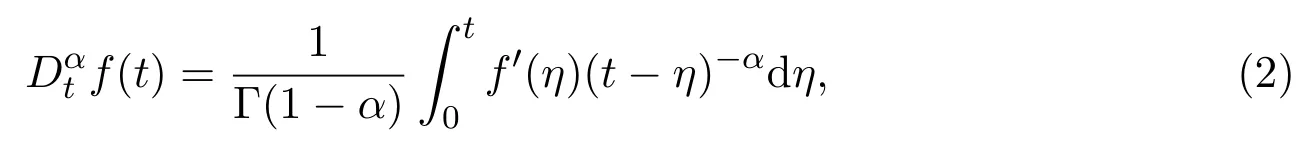
where Γ is the Gamma function,αis the temperature fractional derivative parameter.Under the boundary layer approximation and the assumption that the viscous dissipation is neglected,the momentum and energy equations for the incompressible flow of a second-grade fluid are
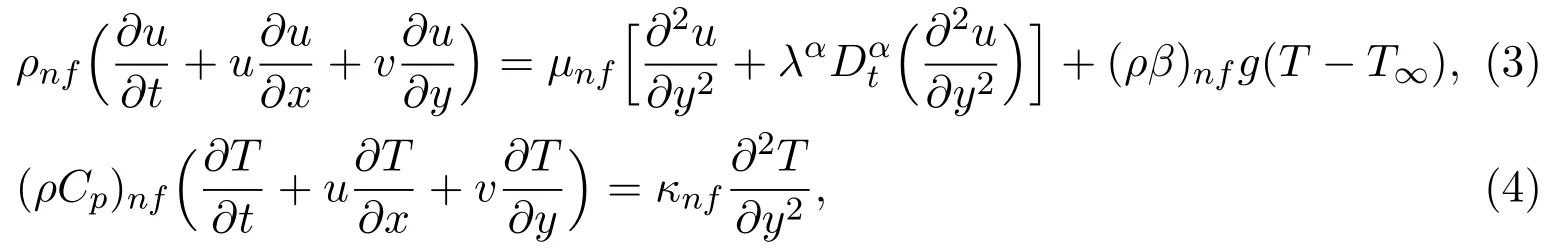
whereuandvare the velocity components alongxandydirections respectively,Tis temperature,ρnfis the density of the nano fluid,βnfand(Cp)nfrespectively stand for the coefficient of thermal expansion and the specific heat at the constant pressure.µnfis the viscosity of the nano fluid.Further,the expressions ofρnf,µnf,(ρβ)nfand(ρCp)nfare given[19-22]as follows:
whereφis the nanoparticle volume fraction,the subscriptsnf,fandprespectively represent the nano fluid, fluid,and nanosolid particles.Moreover,thermal conductivityκnfis given[23]by
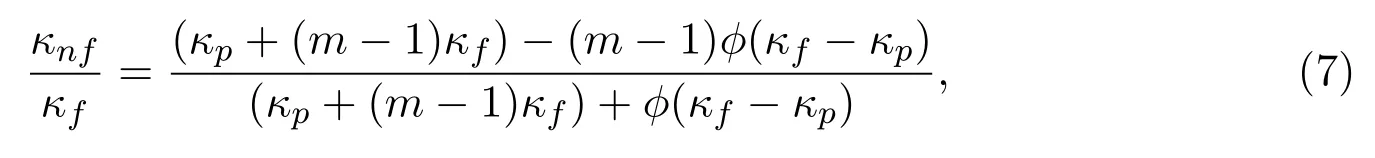
wheremis the nanoparticle shape factor.The thermophysical properties of the base fluid and nanoparticle are given in Table 1[24].Five different types of nanoparticle shapes including sphere,hexahedron,tetrahedron,column and lamina are considered,and the corresponding values ofmfor the different shapes are shown in Table 2[25].

Table 1:Physical properties of fluid and nanoparticles

Table 2:Values of shape factor for different nanoparticle shapes
The initial and boundary conditions for this problem are
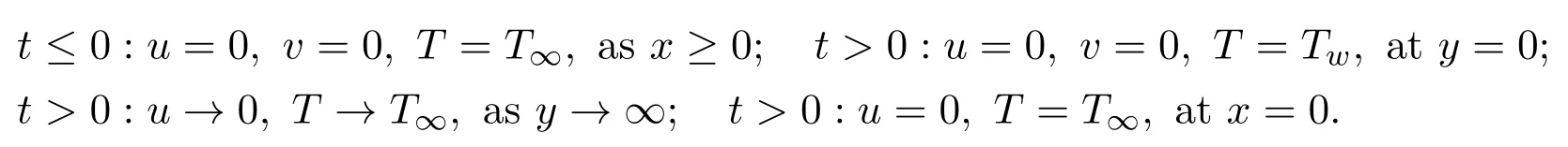
The dimensionless variables are introduced in the following forms:
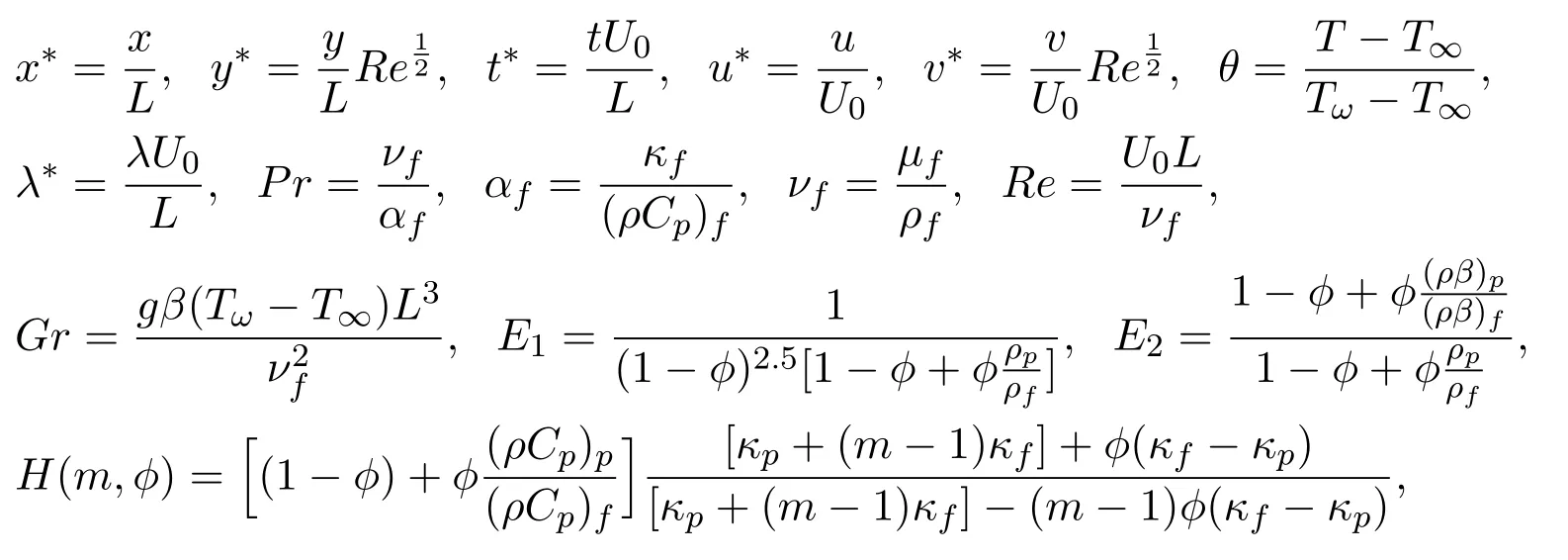
whereReis the generalized Reynolds number,Pris the Prandtl number,νis the kinematic viscosity,andGris the Grashof number.Omitting the dimensionless mart∗for brevity,the governing equations of continuity,momentum and energy can be written as
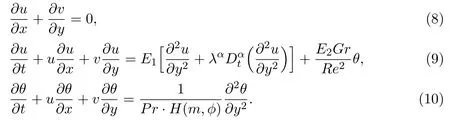
The corresponding boundary conditions become
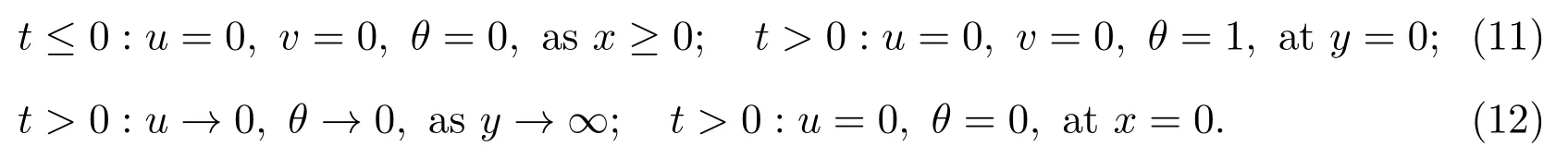
The physical quantity of interest is the local Nusselt number,which is defined[26]as

whereqwis the heat flux from the flat plate,given by

The corresponding dimensionless parameters are given by

Similarly,the average Nusselt number satisfies:
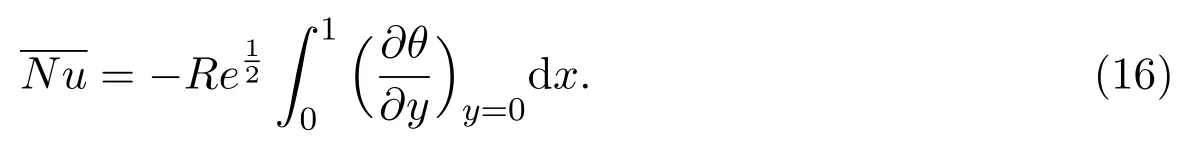
3 Numerical Techniques
In view of the initial conditions and boundary conditions,the numerical solutions of equations(8)-(10)are defined asat the mesh points(xi,yj,tk).Definexi=i∆x(i=0,1,2,···,M),yj=j∆y(j=0,1,2,···,N)andtk=k∆t(k=0,1,2,···,R),where ∆x=L/Mand ∆y=Ymax/Nare space steps,∆tis time step.Based on the definition of Caputo fractional derivative operate,the time fractional derivative(0<α<1)is discretized by using theL1-algorithm as[27]
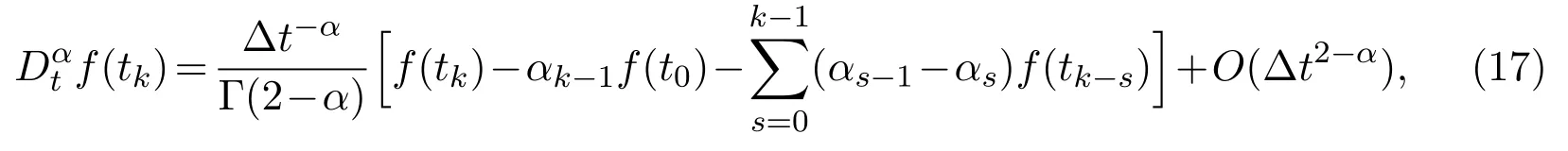
whereαs=(s+1)1−α−s1−α(s=0,1,2,···,R).The integer-order terms in the governing equations are discretized as
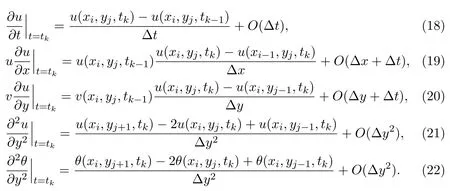
For simplicity,note
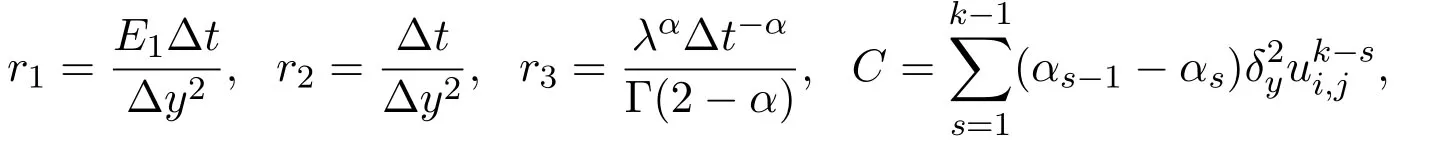
Finally,the iteration equations are achieved as follows:
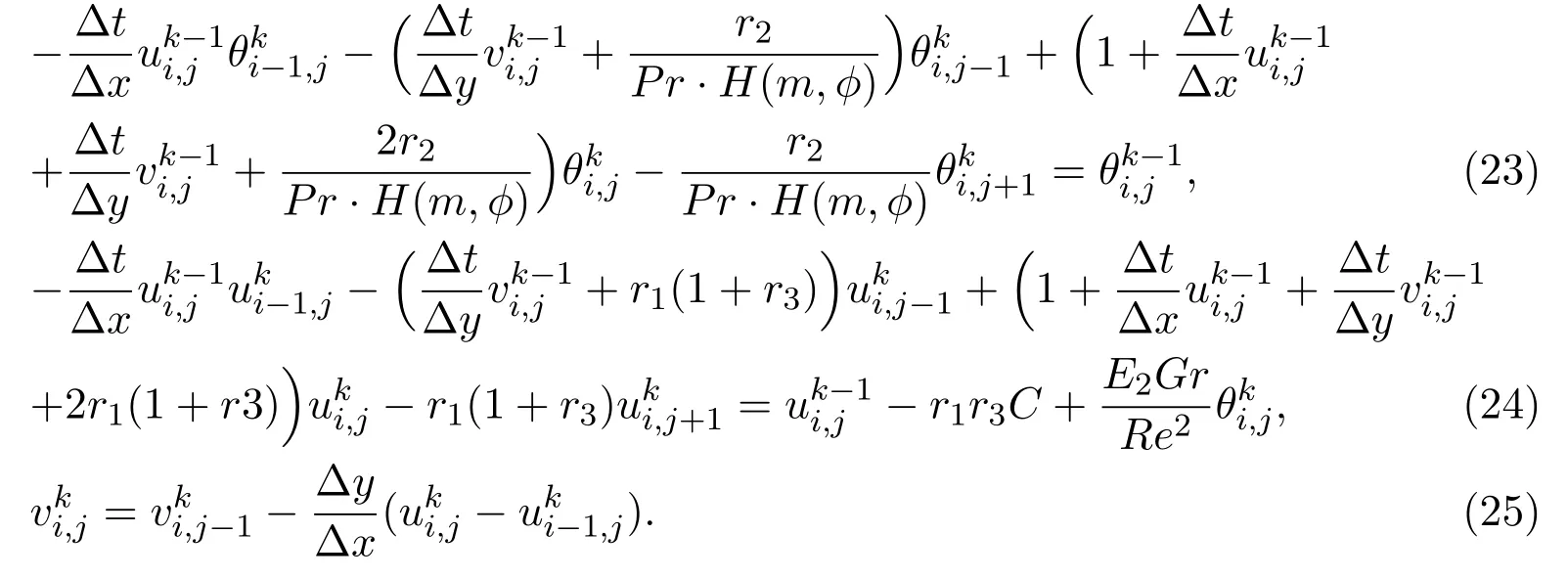
4 Results and Discussion
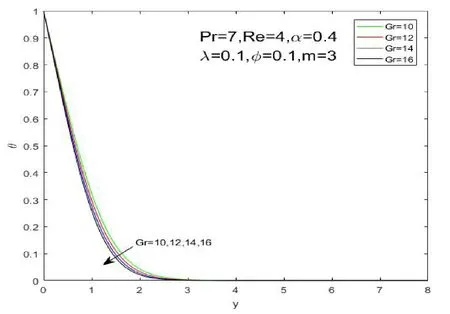
Iteration equations(23)-(25)can be written in the tri-diagonal systems,which were solved by the Thomas algorithm[28].The iteration tends to be stable when the interpolation betweenuandθis less than 10−5at two adjacent time steps.The calculation area can be seen as a rectangle withxmax=2 andymax=8,whereymaxcorresponds toy→∞.In the calculation process,the space and time steps are fixed as∆x=0.02,∆y=0.08 and∆t=0.15.As shown in Figure 1,the resulting numerical solution is stable and convergent by comparinguandθof different grid sizes.
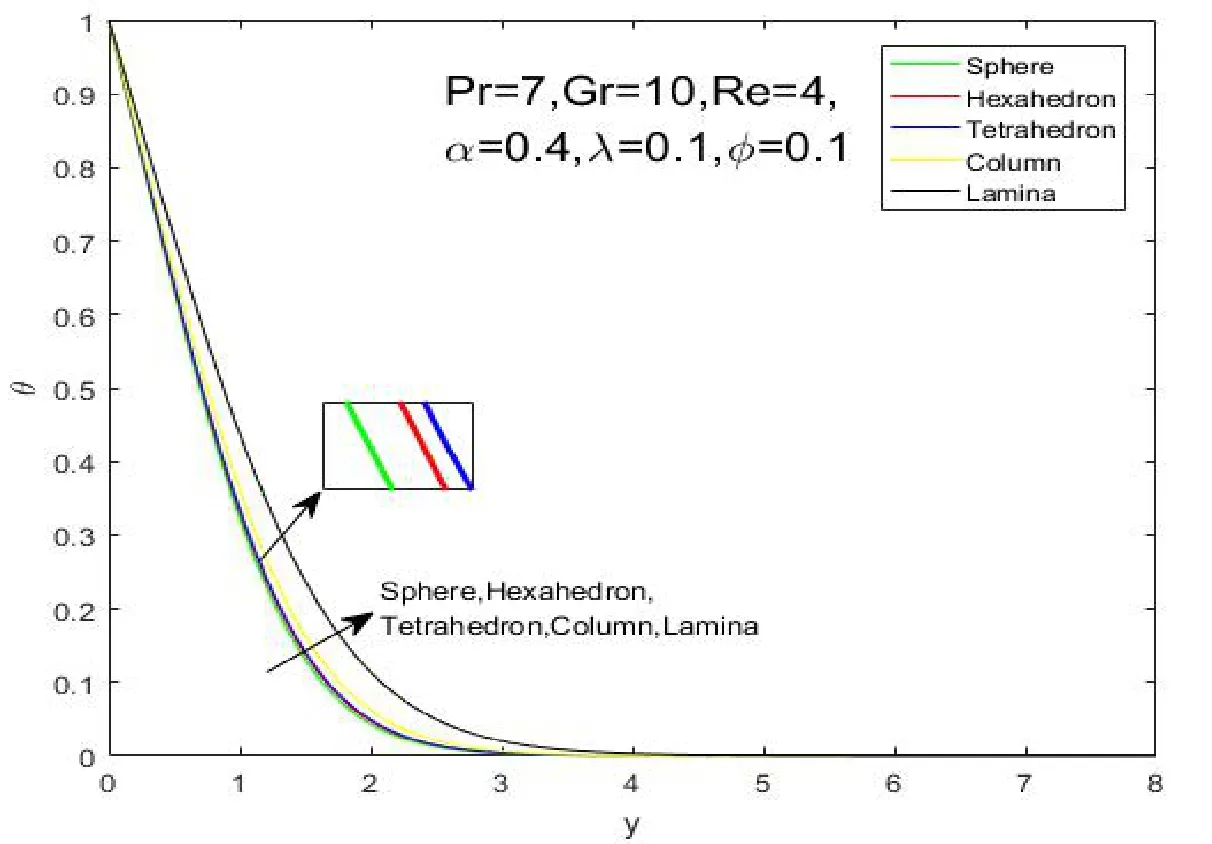
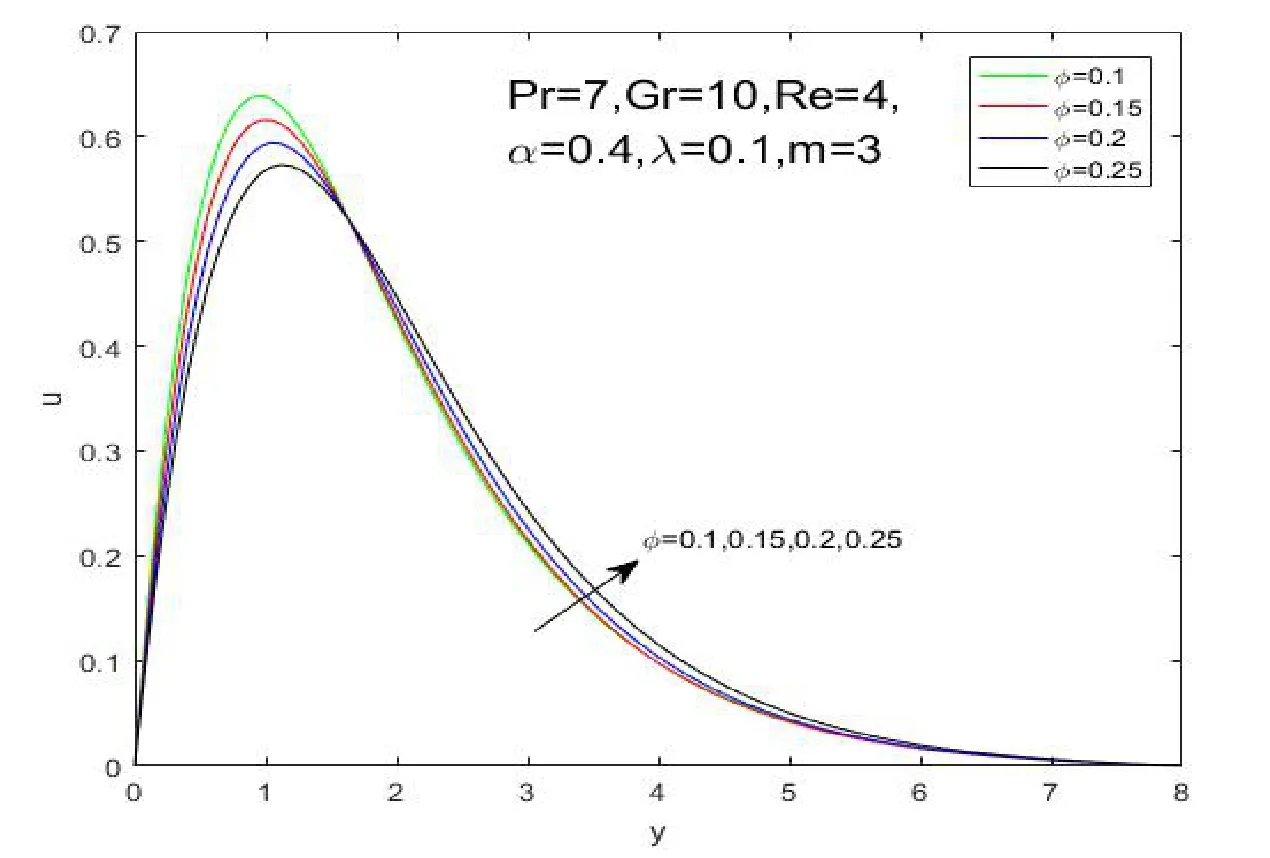
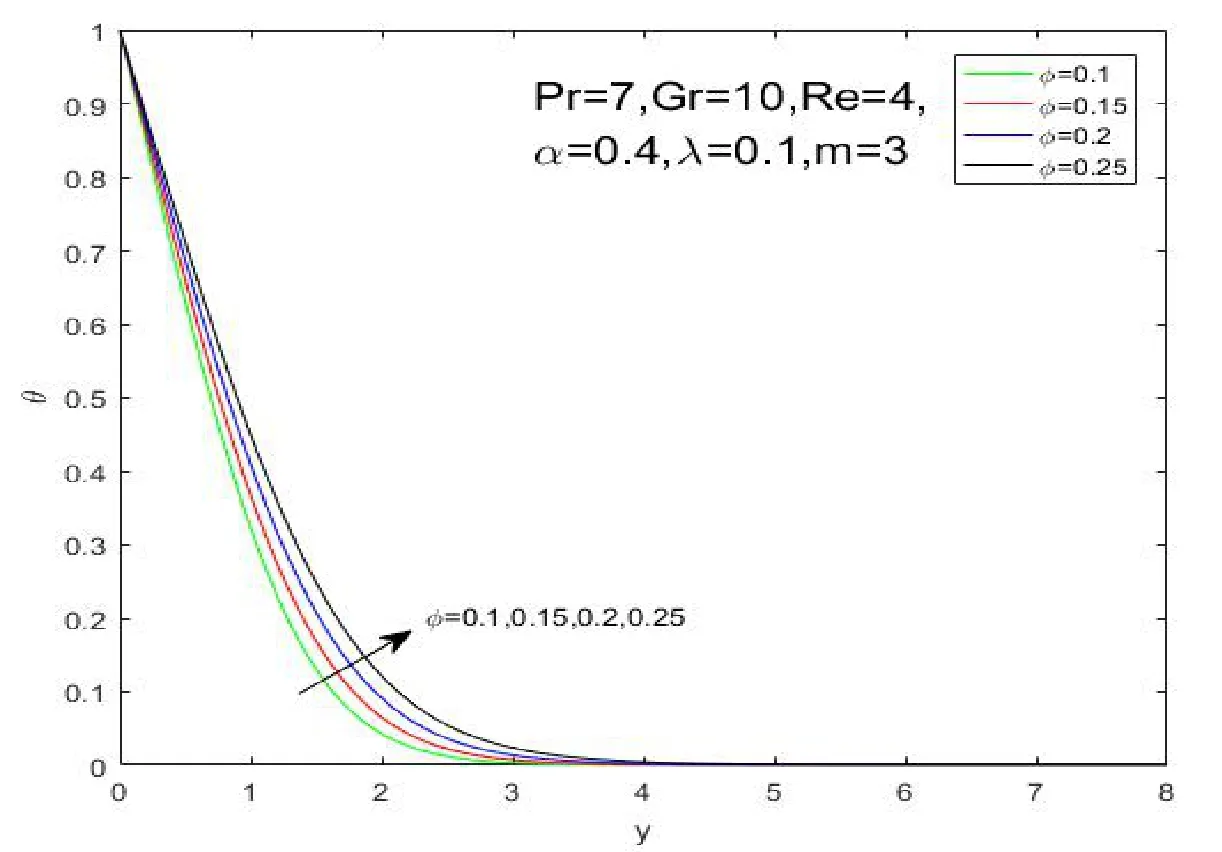
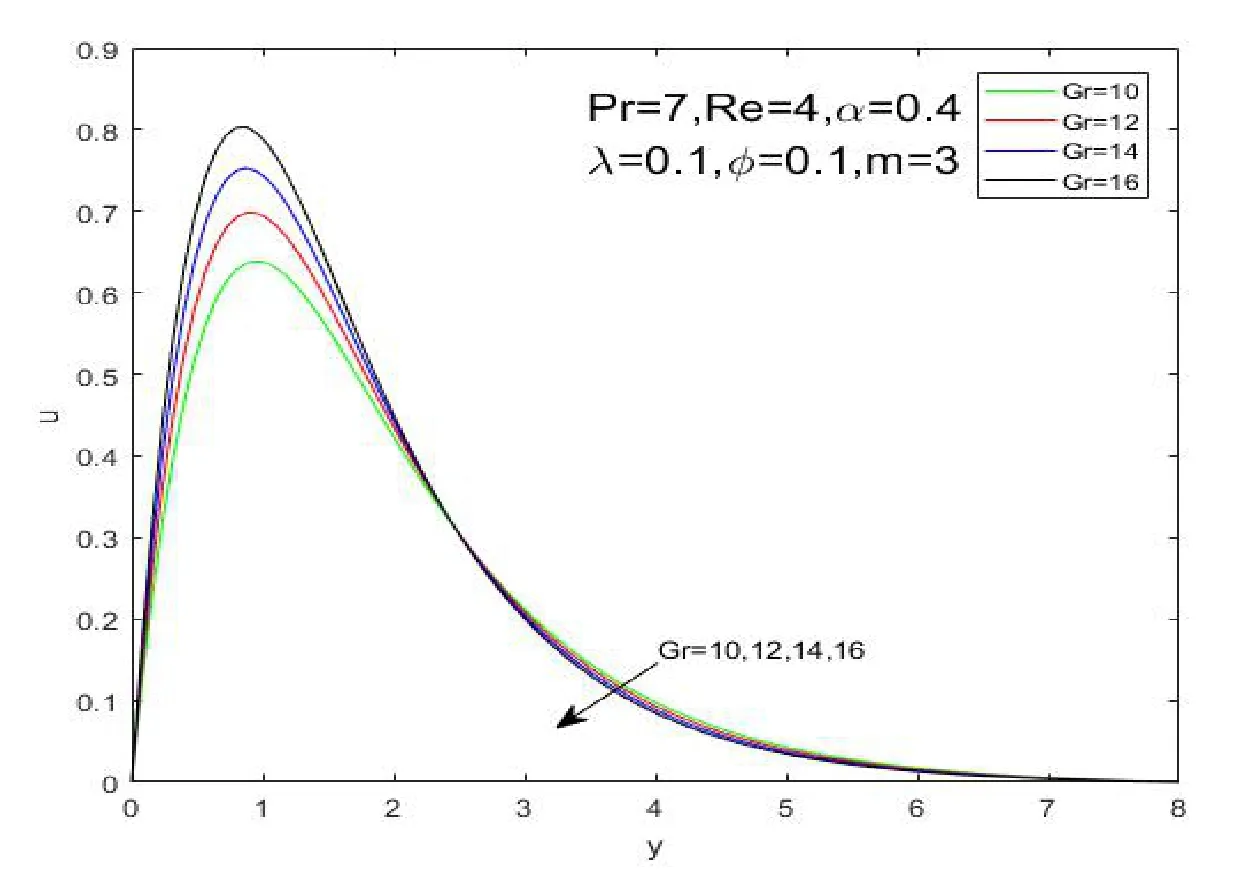
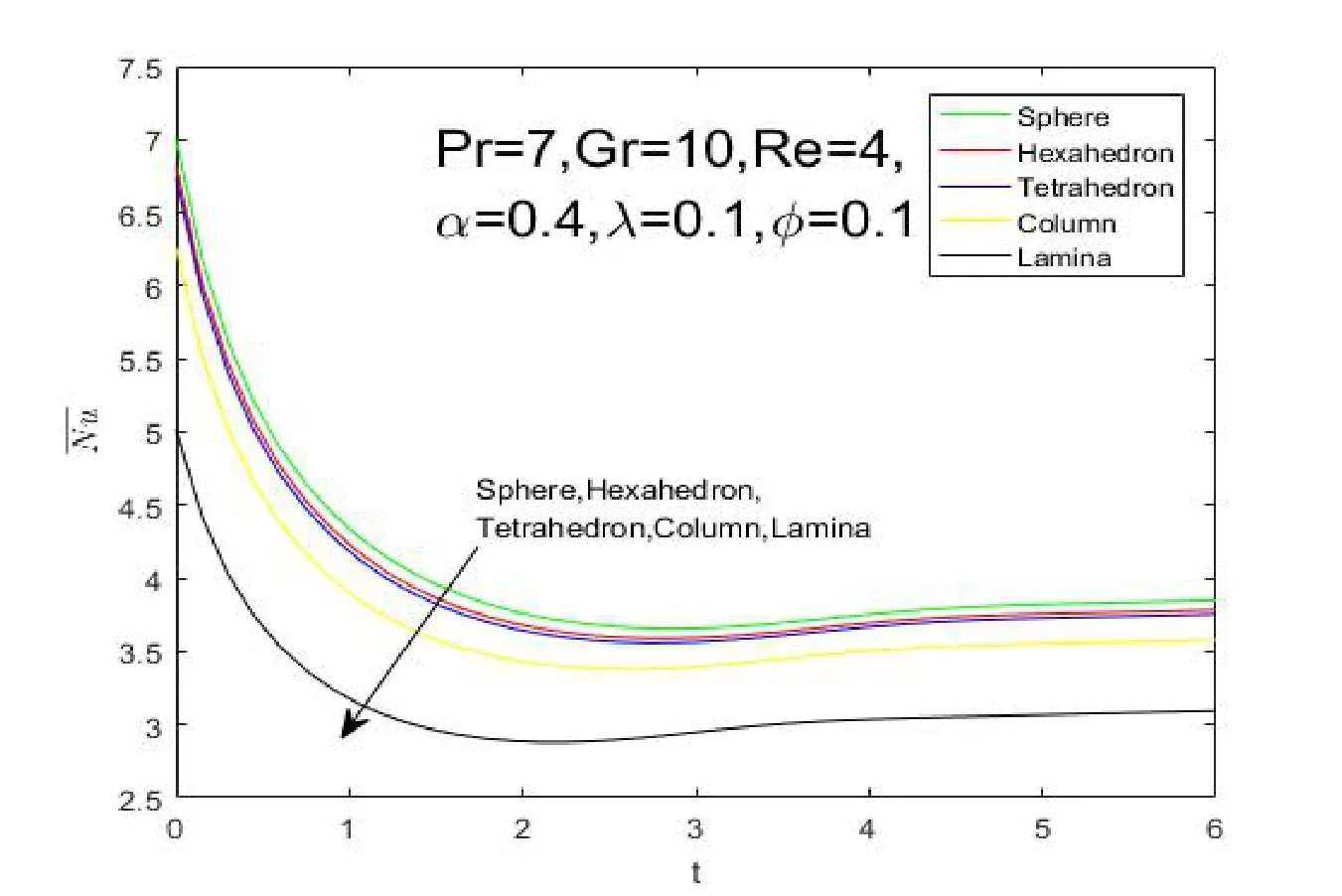
It is revealed from Figure 2 that the nanoparticle shape has a significant impact on temperature and heat transfer of the nano fluid.It can be observed that temperature profile declines uniformly with the decreasing ofm.The results imply that sphere Figure 1:Grid independence test for different mesh sizes Figure 2:influence of shapes on temperature profiles Figure 3:influence of α on velocity profiles Figure 4:influence of α on temperature profiles The influence ofφon the velocity and temperature profiles are illustrated in Figures 5 and 6.It is observed from Figure 5 that the maximum values of the velocity profiles reduce as the nanoparticle volume fractionφrises,because the nanoparticles are solid particles,which bring the additional flow resistance.As shown in Figure 6,it can be observed that the temperature and thermal boundary layer thickness increase asφrises.These phenomenons indicate that an increase in the number of nanoparticles weakens heat and momentum transfer of fluid. Figure 5:influence of φ on velocity profiles Figure 6:influence of φ on temperature profiles The Grashof number approximates the ratio of buoyancy to viscous forces acting on the fluid.The impacts of the Grashof number on velocity and temperature profiles are respectively shown in Figures 7 and 8.It is found that the maximum value of the fluid velocity rises as the Grashof number rises as shown in Figure 7.However,the values of temperature and the thermal boundary layer thickness diminish asGrevolves.This is due to the fact that the parameterGris a non-dimensional physical quantity to reflect buoyancy on the fluid,which provides the power of flow. Figure 7:influence of Gr on velocity profiles The average Nusselt number is an important physical quantity to investigate the heat transfer of the flow.The impact ofmon the average Nusselt number is displayed in Figure 9.This result indicates that sphere>hexahedron>tetrahedron>column>lamina for the average Nusselt number.It is due to the fact that the ratio of thermal conductivityκnf/κfincreases withm.The value of the average Nusselt number for the sphere nanoparticle is the largest among the five different shapes,which is in accordance with the results illustrated by Figure 2.It is worth noting that the average Nusselt number drops rapidly first and then slowly rises until it stabilizes. Figure 8:influence of Gr on temperature profiles Figure 9:influence of shapes on the Average Nusselt number The paper is concerned with the natural convection flow of a fractional secondgrade nano fluid.The effects of nanoparticle shapes on the flow and heat transfer are probed in this paper.The worth mentioning points are obtained as follows: 1)Sphere nanoparticle has the minimum thermal boundary layer thickness and the maximum average Nusselt number.Therefore,the heat transfer of spherical nanoparticles is superior to other nanoparticles. 2)The velocity increases withybefore reaching the maximum values with the impact ofα.Then the velocity profiles intersect at a point after the turning point,which implies the fractional nano fluids model with Caputo time derivatives has a short memory of previous states. 3)The nanoparticle volume fractionφhas an opposite effect on temperature and velocity profiles.The maximum values of the velocity profiles reduce as the nanoparticle volume fractionφrises because solid particles bring the additional flow resistance. 4)The Grashof number has a similar influence on velocity and temperature profiles withα.The values of temperature and the thermal boundary layer thickness diminish asGrevolves because of the thermal buoyancy effect.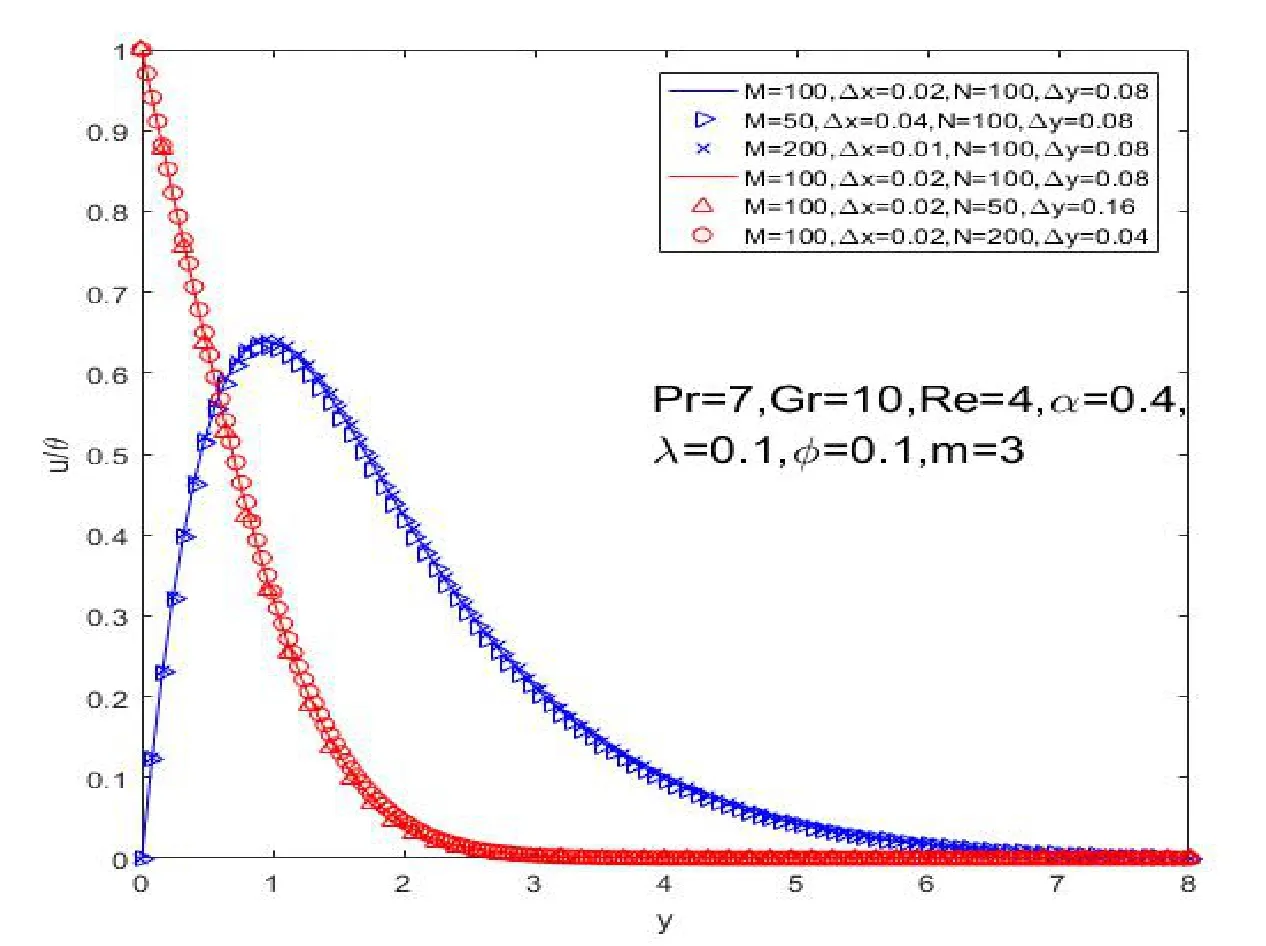
5 Conclusion
杂志排行
Annals of Applied Mathematics的其它文章
- TRAVELING WAVE SOLUTIONS FOR A PREDATOR-PREY MODEL WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE∗†
- THE EFFECT OF REFUGE AND PROPORTIONAL HARVESTING FOR A PREDATOR-PREY SYSTEM WITH REACTION-DIFFUSION∗†
- POSITIVE SOLUTIONS TO A BVP WITH TWO INTEGRAL BOUNDARY CONDITIONS∗†
- BICYCLIC GRAPHS WITH UNICYCLIC OR BICYCLIC INVERSES∗†
- BIFURCATION ANALYSIS OF A CLASS OF PLANAR PIECEWISE SMOOTH LINEAR-QUADRATIC SYSTEM∗†
- NEW OSCILLATION CRITERIA FOR THIRD-ORDER HALF-LINEAR ADVANCED DIFFERENTIAL EQUATIONS∗†
