POSITIVE SOLUTIONS TO A BVP WITH TWO INTEGRAL BOUNDARY CONDITIONS∗†
2020-09-14KaikaiLiuYunruiYangYangYang
Kaikai Liu,Yunrui Yang,Yang Yang
(School of Mathematics and Physics,Lanzhou Jiaotong University,Lanzhou 730070,Gansu,PR China)
Abstract
Keywords integral boundary conditions;positive solutions;cone
1 Introduction
Boundary value problems(BVPs)for ordinary differential equations have wide applications in many scientific areas such as physics,mechanics of materials,ecology and so on.For example,deformations of elastic beams can be represented for some fourth-order BVPs,and there are some appealing results[1–3]can be referred.
Especially,much attention has been drawn to BVPs with integral boundary conditions[4–9]recent years because of their applications in thermodynamics and chemical engineering.In 2011,by global bifurcation theory and the Krein-Rutman theorem,Ma[4]investigated positive solutions to a class of BVP with integral boundary conditions.Hereafter,based on the famous Krasnoselskii’s fixed-point theorem,Lv[5]considered the monotone and concave positive solutions to the following integral BVP
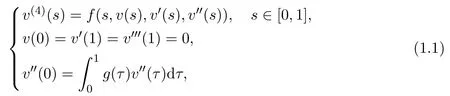
wheref∈C([0,1]×[0,+∞)×[0,+∞)×(−∞,0],[0,+∞)),g∈C([0,1],[0,+∞)).For more this kind of results,one can refer to[7–9].
Nevertheless,there are few results on multiplicity and the properties of positive solutions to BVPs with integral boundary conditions.Recently,Yang[6]investigated the multiplicity of positive solutions to a fourth-order integral BVP.Motivated by Yang’s ideas in[6]and based on the work of Lv[5],this paper deals with the following BVP with two integral boundary conditions
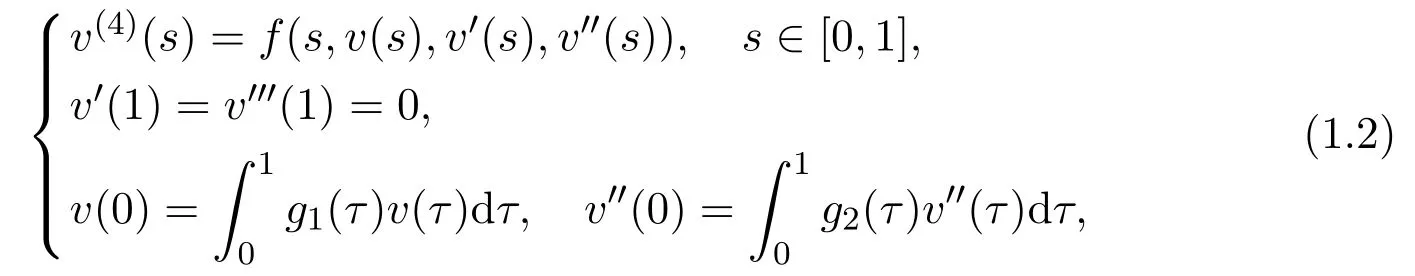
and the existence and multiplicity of positive solutions are thus established.Notice that(1.2)is reduced to(1.1)wheng1≡0 in(1.2),and therefore we generalize the result of one positive solution in[5]to the case of multiple positive solutions.Moreover,some results of positive solutions to integral BVPs we mentioned in[4,5,9]are also improved.
2 Preliminaries
We first state several notations and lemmas in this paper.
We always assume that,throughout this paper,f:[0,1]×[0,+∞)×[0,+∞)×(−∞,0]→[0,+∞)andg1,g2:[0,1]→[0,+∞)are all continuous.Furthermore,

Lemma 2.1[10](Guo-Krasnoselskii’s fixed-point theorem)Let E be a Banach space,J⊂E is a cone.Suppose that I1and I2are bounded open subsets of E withθ∈I1and,and letbe a completely continuous operatorsuch that either
(i)∥Lv∥≥∥v∥,v∈J∩ ∂I1and∥Lv∥ ≤∥v∥,v∈J∩ ∂I2;or
(ii)∥Lv∥ ≤∥v∥,v∈J∩ ∂I1and∥Lv∥≥∥v∥,v∈J∩ ∂I2
holds,then L has a fixed point in.
LetC2[0,1]be bestowed on the maximum norm
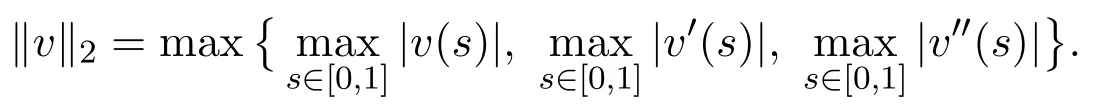
Similar to Lemma 2.1 in[5],we obtain the following result by a direct computation.
Lemma 2.2If y∈C[0,1],then the following BVP
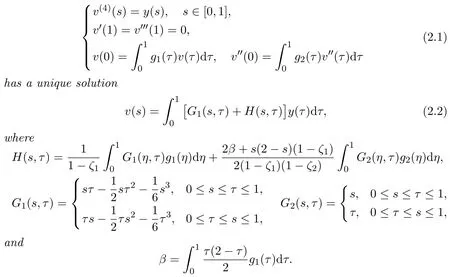
Lemma 2.3[5]Let G1(s,τ)be as in Lemma2.2.For s,τ∈[0,1],
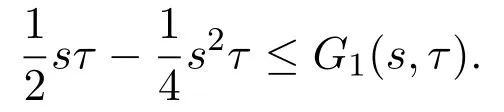
Lemma 2.4If,then the unique solution v=v(s)to theBVP(2.1)satisfies the following assertions:
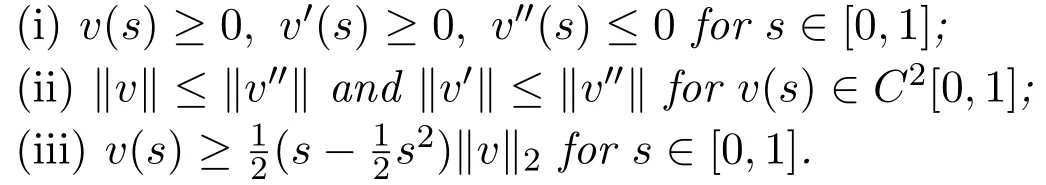
ProofThe proof of(i)is analogous to Lemma 2.3 in[5]and so we omit it here.
(ii)By the facts thatv′(1)=0 andv′(s)≥0 fors∈[0,1],it follows that
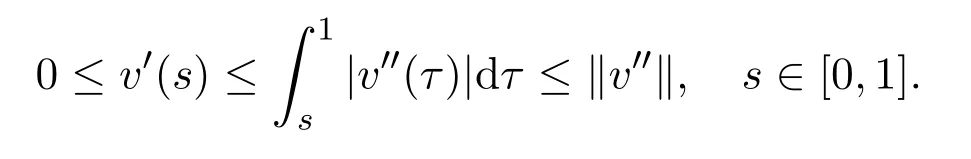
Therefore,∥v′∥≤∥v′′∥.
In turn,according to the facts thatfor anys∈[0,1],

and
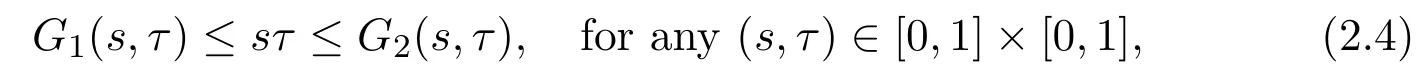
we get

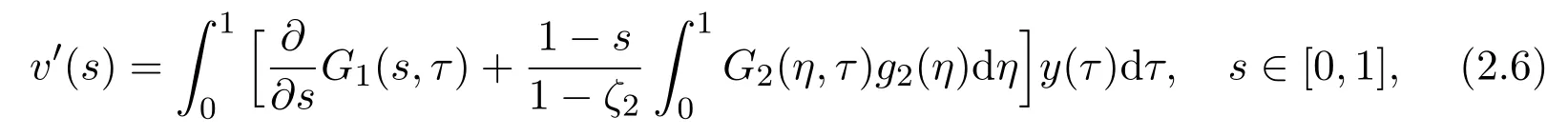
and
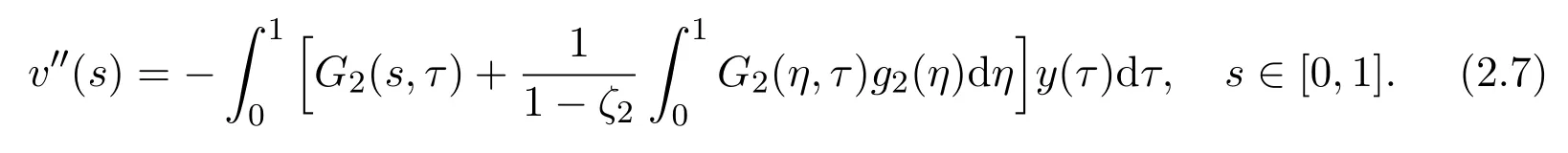
Therefore,by(2.2),(2.4)-(2.7),one has
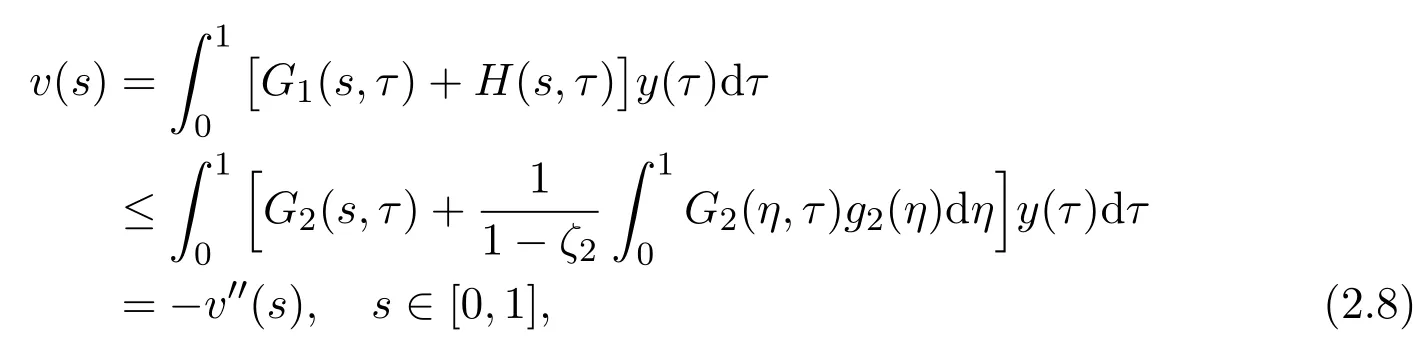
which means that∥v∥≤∥v′′∥.Combining the fact that∥v′∥≤∥v′′∥,it is natural that

(iii)By(2.7),we have
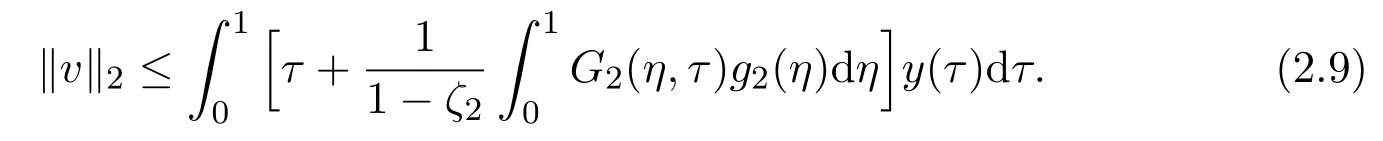
Moreover,by Lemma 2.3 and(2.2),we obtain
Define a cone J inC2[0,1]by
and define an operatorL:J→C2[0,1]by
Clearly,v(·)is a positive solution with monotonicity and concavity of the BVP(1.2)if and only ifv(·)is a fixed point ofL.In addition,in view of the factL(J)⊂Jand by Lemma 2.4,it is trivial to establish the following result:
Lemma 2.5L:J→J is completely continuous.
3 Existence of One Positive Solution
In this section,our purpose is to investigate the existence of one positive solution to the BVP(1.2).
Theorem 3.1There is at least one monotone and concave positive solution to the BVP(1.2)if either
holds.
Proof(i)Since,there exists a numberδ1>0 such that

From the continuity offand the definition of,there is a numberλ>0 such that,fors∈[0,1]andυ0+υ1−υ2∈[0,λ],
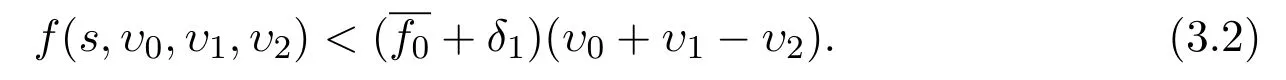

Therefore


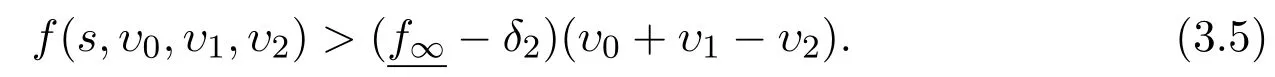
LetI2={v∈C2[0,1]:∥v∥2<Λ}for allv∈J∩ ∂I2,by Lemma 2.3,(3.4)and(3.5),we have
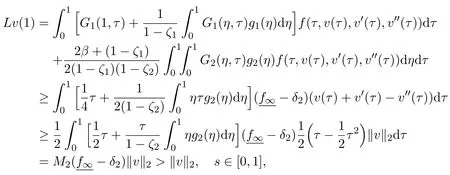
which indicates
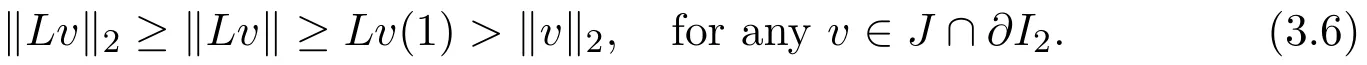
Therefore,the operatorLhas at least one fixed pointby(3.3),(3.6)and Lemma 2.1,that is,there is at least one monotone and concave positive solution to the BVP(1.2).
The proof of(ii)is much similarly,and thus we omit it here.The proof is complete.
Corollary 3.1There is at least one monotone and concave positive solution to the BVP(1.2)if either
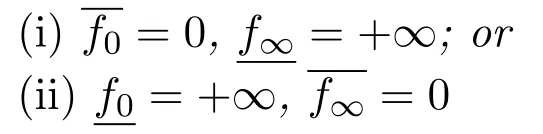
holds.
Example 3.1Consider the following BVP
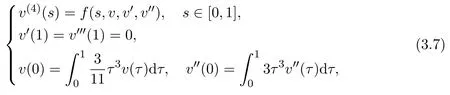
where
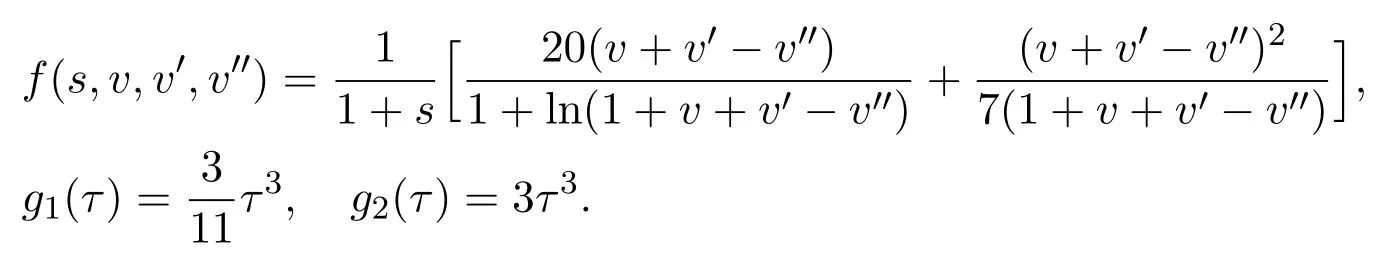
It is not difficult to examine thatf,g1andg2satisfy the assumptions of Section 2 in this paper.By some calculations,we also obtain thatand,which means(ii)of Theorem 3.1 holds.Therefore,there exists at least one monotone and concave positive solution to the BVP(3.7)by Theorem 3.1.
4 Existence of Multiple Positive Solutions
In this section,our aim is to establish the existence of multiple positive solutions to the BVP(1.2).
Theorem 4.1There are at least two monotone and concave positive solutions to the BVP(1.2)if one of the following conditions holds:

Proof(i)LetE=C2[0,1],,I2={v∈E:∥v∥2<Λ}.By Theorem 3.1,it follows that∥Lv∥2≤∥v∥2whenv∈J∩ ∂I1orv∈J∩∂I2.ChooseI3={v∈E:∥v∥2 The proof of(ii)is much similar,so we omit it here.The proof is complete. Corollary 4.1There are at least two monotone and concave positive solutions to the BVP(1.2)if either holds. Example 4.1Consider the following BVP where It is not difficult to check thatf,g1andg2satisfy the assumptions of Section 2 in this paper.By some calculations,we also obtainwhich implies condition(ii)of Corollary 4.1 holds.Therefore,there are at least two monotone and concave positive solutions to the BVP(4.1)by Corollary 4.1.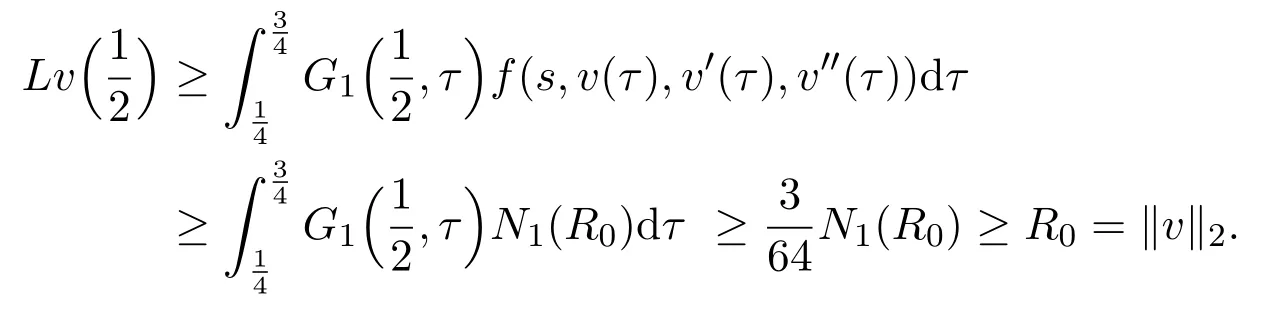

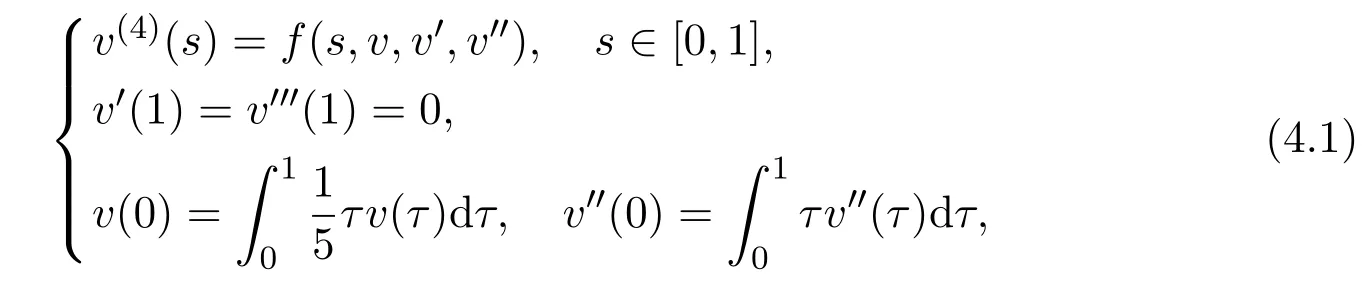
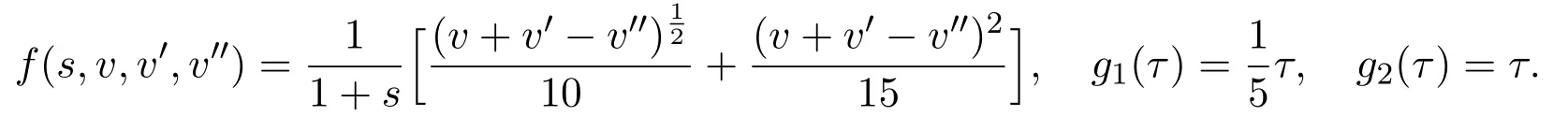
杂志排行
Annals of Applied Mathematics的其它文章
- TRAVELING WAVE SOLUTIONS FOR A PREDATOR-PREY MODEL WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE∗†
- THE EFFECT OF REFUGE AND PROPORTIONAL HARVESTING FOR A PREDATOR-PREY SYSTEM WITH REACTION-DIFFUSION∗†
- UNSTEADY NATURAL CONVECTIVE BOUNDARY LAYER FLOW AND HEAT TRANSFER OF FRACTIONAL SECOND-GRADE NANOFLUIDS WITH DIFFERENT PARTICLE SHAPES∗†
- BICYCLIC GRAPHS WITH UNICYCLIC OR BICYCLIC INVERSES∗†
- BIFURCATION ANALYSIS OF A CLASS OF PLANAR PIECEWISE SMOOTH LINEAR-QUADRATIC SYSTEM∗†
- NEW OSCILLATION CRITERIA FOR THIRD-ORDER HALF-LINEAR ADVANCED DIFFERENTIAL EQUATIONS∗†
