分类思想在图形教学中的渗透

2020-09-12陈建忠

数学教学通讯·小学版 2020年8期

陈建忠

摘要：分类思想广泛运用于小学数学教材之中，在初级阶段中占据着十分重要的地位。提高分类思想在数学教学中的广泛应用，可以让学生领悟思想方法，提升教学质量。文章从经历分类活动、讨论分类方法和彰显分类结果等三个方面阐述图形教学中渗透分类思想的教学实践与思考。

关键词：图形教学;分类活动;分类方法;分类思想

古往今来，人们对事物的认识一般是从对事物的区分开始的。分类思想不仅是重要的数学逻辑方法，同时也是数学思想中一种重要的思想方法。教材中多处都出现了渗透分类思想的教学，并贯穿于整个小学数学教学内容中，具有明显的探究性、逻辑性和综合性，可以让学生在学习相关知识时，更清晰地掌握其知识本质，同时对学生探究能力和创新精神的培养有巨大的推动作用。

在现实教学中，不少教师也进行了分类思想的渗透，但却不能有序系统地进行。事实上，分类思想的渗透并非一蹴而就的，需要基于学生的年龄特征，随着其认知水平的不断提高和数学知识的逐渐积累而逐步渗透的。在图形教学中切入渗透分类思想，可以沟通图形间的联系，使学生建构图形知识网络，发展空间观念。本文将以教材中的图形知识为主线，充分挖掘其中所蕴含的分类思想，以期在图形教学中更能充分地发挥分类思想的教育教学价值。

一、经历分类活动，深化概念理解

小学数学中，不少数学概念都能在生活中找寻到它的原型，生活中随处可以见到各种概念现象。因此，概念教学中，教师可以通过鲜活的感性素材，为学生打造丰富的概念背景，引导学生进行比较、分析、整理和交流等活动，让学生亲历分类活动，从而在更高层次上归纳概括概念本质，形成良好的认知结构。

案例1：以“垂线与平行线”的单元教学为例。

第一次分类活动：感知。

（1）画一画：请试着在点子图上画出两条直线。（画出尽可能多的不同画法）

（2）分一分：依据一定的标准，将所有画出的两条直线进行分类，并记录分类结果。（学生生成如图1、图2、图3所示的三种情形）

设计意图：通过活动设计，让学生对同一平面内的两条直线关系形成一个初步的认识，同时形成一定的质疑。

第二次分类活动：分析。

（1）进行对比，明晰“看似不相交，实则相交”的情形。出示图1（生1）、图2（生2）的两种分法，并请各自说一说分类依据、分类标准和分为几种。引导学生通过实践、思考、分析、讨论和辨析生1的分法中④和⑧与生2的分法中④和⑤的不同。最终突破问题本质，并及时修正生1的结论。

（2）再次对比，理清垂直和相交的特殊关系。再次引导学生对比生1分类中的③⑦和生2分类中的②⑧，同时思考：同一平面内的两条直线位置关系的类别有哪些？你是依照什么标准分类的？通过多个问题的思考和探究，帮助学生理清垂直特殊位置关系的归宿，深化学生的认知结构。

（3）再次分类，梳理知识。出示生3的分法图3，并引导学生思考和讨论以下问题：生3的分类方法与刚才探究的分类方法有何异同点？有什么新发现呢？

学生经过思考后，形成如图4所示的思路。同时教师再次抛出问题：将①②⑤再分为两类，可行吗？请说明理由。

设计意图：通过再次抛出问题，引发学生的讨论，深化学生对同一平面内的两条直线的关系有一个深刻的认识，化解这一知识中的难点问题，明晰判断垂直的关键之处。

第三次分类活动：深化。

变式训练：请试着画一画各种不同方位相交而成直角的情况。

设计意图：通过变式训练有效克服学生的思维定式，深化学生的认识。

在教学过程中，教师通过适宜的教学策略，让学生参与分类活动，突破概念认知障碍，深化和提升概念理解水平，形成良好的认知结构，从而铺平概念学习的道路。

二、讨论分类方法，充分积累经验

在渗透分类思想的过程中，教师要让学生理清分类的来龙去脉，分类的标准以及如何合理分类。这些问题是需要学生通过对分类结果的讨论和交流来沟通知识间的联系，认清思考的脉络，充分展现思维过程，体验不同标准下的分类结果。

案例2：课题“三角形的分类”。

师：请大家试着根据角的特点将以下三角形进行分类。（如图5）

生1：可以分为三类，第一类是锐角三角形：②和④;第二类是直角三角形：①和⑥;第三类是钝角三角形：③和⑤。

师：不错。还有其他分类方法吗？

生2：可以分为两类，第一类是含有三个锐角：②和④;第二类是含有两个锐角：①③⑤和⑥。

生3：我认为还可以这样分类：第一类是①和⑥，其余为第二类。

师：那和大家说说你的分类依据呢？

生3：我是按照……（由于思维卡壳，无法继续进行分析）

生4：我觉得他是按照有无直角来分类的。

……

设计意图：讨论分类方法时，学生从自身的理解出发，创造性地进行思考、联想和理解，将图5中的三角形进行不同方法的分类，呈现不同的分类结果，并交流分类方法的思考，从而实现对分类标准重要性的解读。在数学过程中，需要我们教师给予学生充足的时间和空间去讨论，培养学生良好的思维能力，能从宏观的角度感悟分类的本质，形成结构良好的认知，积累有关分类的活动经验。当然，上述案例中最合理的分类情况自然是分为三类，这样的分类方式是指向图形的本质特征，且利于锐角三角形、直角三角形和钝角三角形概念的抽象。

三、彰显分类结果，感悟分类思想

在图形学习中，不少知识点都是单一的、零散的，在教学过程中，教师宜通过一定的教学策略，勾画知识技能框架，为学习提供基本线索，及时、适时地进行知识梳理，让学生领悟到知识框架和完善知识网络，从而感悟分类思想。

案例3：单元课题“三角形、平行四边形和梯形”。

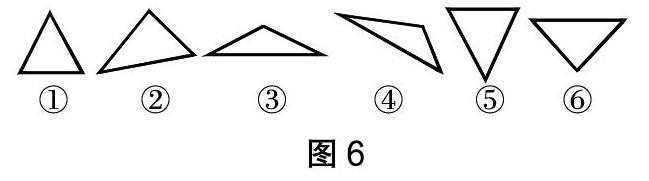
问题呈现：如图6，图中各是什么三角形？基于角的特点该如何分类？

师：请独立思考，图6中六个三角形各是什么三角形，并小组合作讨论，如果按角分类，可以如何分？（学生先独立分类，后在小组进行交流）

师：观察图6，并思考从三角形边的特点出发，三角形有什么关系？

生1：以上三角形中，从边的特点出发，有三边都不相等的三角形，如②④;有两条边相等的等腰三角形，如③⑤和⑥;还有三边相等的等边三角形，如①。

师：很好。那大家再试着以图示的方式来描述按角分类的结果。

生2：图7即为按角分类的结果。

师：非常好！如图8，试着根据三角形边的特点，在图中圆圈里描述出它们的关系。

生3：结果见图9。

师：类比观察以上两幅图（图7、图9），可有什么发现？