ARIA 算法的一个新不可能差分路径及相应攻击

欧海文, 王湘南, 李艳俊, 雷亚超

1. 北京电子科技学院, 北京100070

2. 西安电子科技大学, 西安710071

1 引言

ARIA 算法[1]由韩国研究人员设计, 从开始的ARIA 0.8 版、ARIA 1.0 版和ARIA 1.2 版, 确定最终版本为1.2 版. ARIA 算法是分组长度为128 bit 的SPN 型的分组密码[2], 可变密钥长度支持三种类型: 128 bit、192 bit 和256 bit, 迭代轮数分别为12, 14, 16 轮[3]. 采用了与AES 算法[4]相似的结构,很多AES 算法的分析方法也适用于ARIA 算法, 结合ARIA 算法的研究, 实现了对ARIA 算法的不可能差分攻击.

不可能差分分析是由Knudsen 和Biham 分别独立提出[5,6]. 与差分不同, 不可能差分分析的理念是凭借概率为0 的差分特征, 将那些会导致概率为0 的差分出现的候选密钥去除, 因为若使用正确的密钥来对明文进行加密, 不可能得到这样的密文差分特征[3]. 筛除这些候选密钥值, 剩下的就是正确的密钥值.

2 ARIA 算法

2.1 ARIA 算法介绍

ARIA 是分组长度为128 比特的SPN 型分组密码, ARIA 每一轮由3 个部件构成:

(1) 轮密钥加(Round Key Addition, RKA). 由每一轮的输入状态和轮密钥ki两者之间进行异或构成, 而轮密钥ki是由密钥扩展算法得到的.

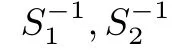
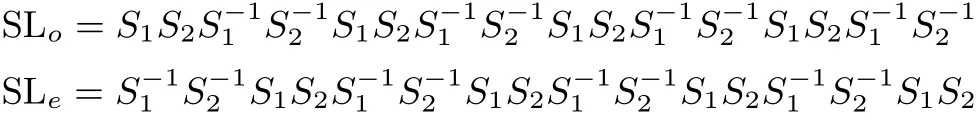
SLo、SLe分别在单数轮中用和在双数轮中用.

(3) 扩散层(Diffusion Layer, DL). 扩散层是一个将16 B 输入(x0,x1,··· ,x15) 映射为16 B 输出(y0,y1,··· ,y15) 的线性函数:(F82)16→(F82)16, 其中:

2.2 符号说明

3 对7 轮ARIA-256 的不可能差分分析

本文是对7 轮ARIA 算法的不可能差分分析, 首先构造了新的4 轮不可能差分区分器, 然后在区分器上构造2 轮前置路径和1 轮后置路径, 得到7 轮不可能差分路径.

3.1 ARIA 算法的2 个性质

命题1 如图1 所示, 存在一明文对, 在字节(4,10) 处差分值非0, 其余字节处差分值为0, 4 轮变换后, 密文对差分特征∆X4不会是如下形式: (f,0,0,0,f,0,f,f,0,f,0,f,0,0,f,f). 这一不可能差分性质

符号 说明 符号 说明第i 个输出C密文 mS P 明文 mo i第i 个SL 输出P′ 16 字节明文的第i 字节 mi,j mi 的第j 字节C′ 16 字节密文的第i 字节 ki,j 第i 个子密钥ki 的第j 字节mI i i第i 个输入 B Byte (字节)

可用下式表示:

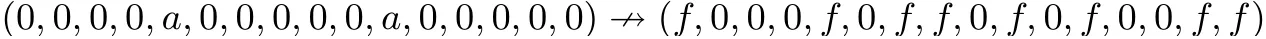
其中a 和f 为任意非零值.

证明: 首先从前两轮正推.

明文对的输入状态满足 (0,0,0,0,a,0,0,0,0,0,a,0,0,0,0,0), 明文对经过第一轮的 RKA 运算后, 由于 RKA 运算不改变差分, 所以差分没有发生改变, 经过第一轮 SL 运算, 差分特征变为:(0,0,0,0,b4,0,0,0,0,0,b10,0,0,0,0,0). 其中, b4和b10为非0 字节.

经过第一轮DL 运算,差分特征为: (b4,0,b4⊕b10,b10,0,b4⊕b10,b10,0,b4⊕b10,0,0,b4,0,b10,b4,b4⊕b10). 再进行RKA 运算和SL 运算, 差分特征为:(c0,0,c2,c3,0,c5,c6,0,c8,0,0,c11,0,c13,c14,c15).

然后进行第二轮的DL 运算,差分特征为:(d0,d1,d2,d3,d4,d5,d6,d7,d8,d9,d10,d11,d12,d13,d14,d15).其中有d1=d15=c2⊕c5⊕c8⊕c15.

再推导(f,0,0,0,f,0,f,f,0,f,0,f,0,0,f,f) 经过两轮逆变换的过程.

经过1 次DL−1变换, 差分特征为:(0,f,0,0,0,0,f,0,0,0,0,0,0,f,f,0).

经过1 次SL−1、RKA−1运算, 差分特征为:(0,e1,0,0,0,0,e6,0,0,0,0,0,0,e13,e14,0).

再进行1 次DL−1运算,差分特征为:(e6⊕e13⊕e14,0,e1⊕e6,e13⊕e14,e14,e1⊕e14,e13,e1⊕e6⊕e13,e1⊕e13,e1⊕e6⊕e14,e6⊕e13,e14,e1⊕e6,e6⊕e13,e14,e1).

其中, e1,e6,e13,e14为非0 值.

最后经过SL−1运算和RKA−1运算,差分特征为:(d∗0,d∗1,d∗2,d∗3,d∗4,d∗5,d∗6,d∗7,d∗8,d∗9,d∗10,d∗11,d∗12,d∗13,d∗14,d∗15). 其中d∗15̸=0, 这是因为SL−1(d∗15)=e1̸=0.

而与d∗1̸=d∗15矛盾, 故是不可能差分路径.

推论1 如图2 所示, 使ms1通过扩散层变换至mo1时, 当ms1差分满足以下五个等式时, mo1在10B(1,2,4,5,7,8,9,10,12,15) 处差分为零的概率为2−24, 而在随机的情况下, 此概率为2−80, 这五个等式分别为:

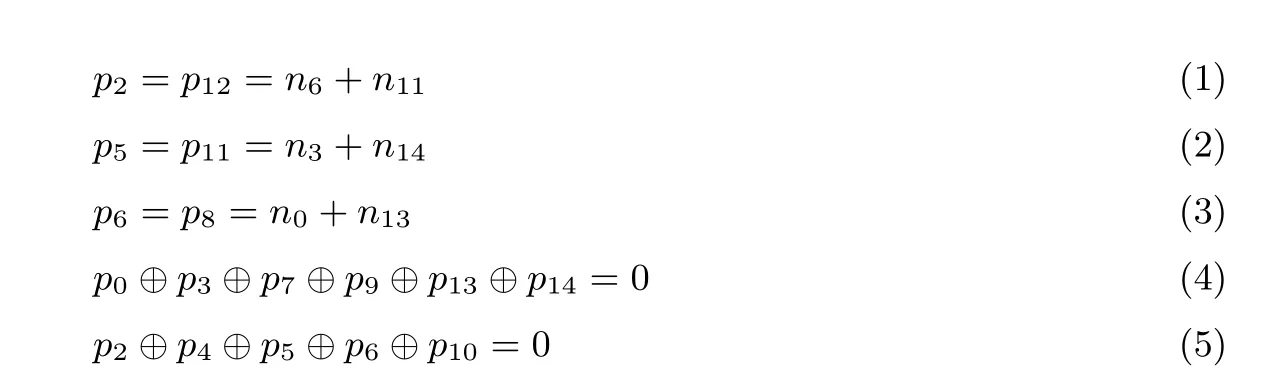
证明: 定义一个在字节(1,2,4,5,7,8,9,10,12,15) 处取值相等, 其余字节差分不为0 的明文空间结构,在输出mo1处,如果存在这样一个结构,通过DL−1操作后,可以得到p2=n6+n11和p12=n6+n11,不管n6和n11为何值, 式(1)以概率1 成立.

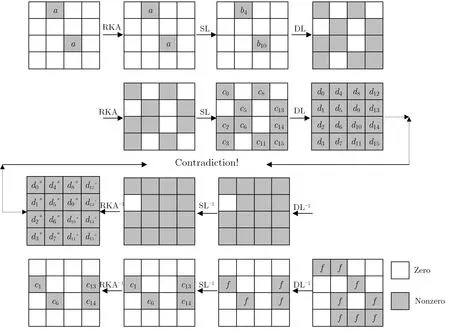
图1 ARIA 算法的4 轮不可能差分分器Figure 1 4-round impossible difference divider of ARIA algorithm

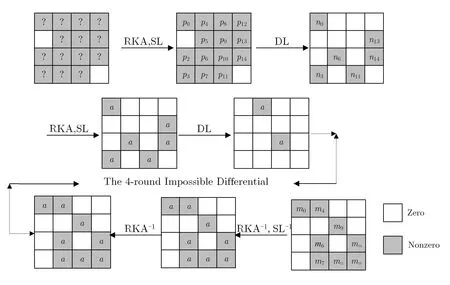
图2 7 轮ARIA 的不可能差分分析路径Figure 2 Impossible differential analysis path of ARIA in 7-rounds

同理, 式(2)和式(3)都成立. 又有

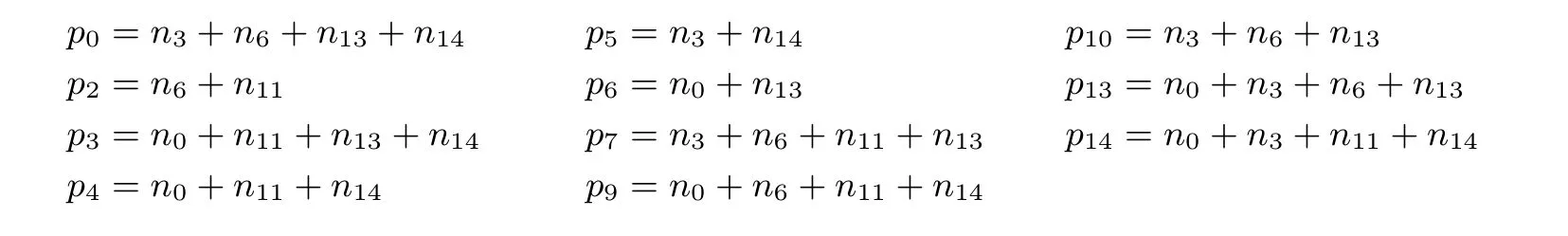
所以, 易证式(4)和式(5)成立.

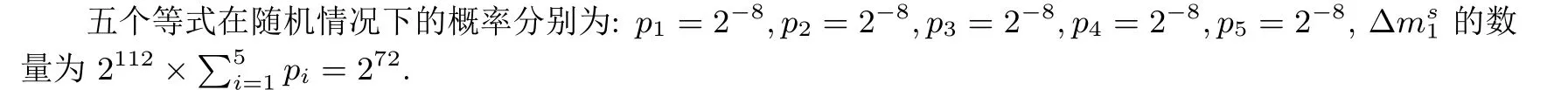
DL 是线性变换, 在mo1处有248个, 故满足以上五个等式的∆mo1的概率为p=248/272=2−24.

3.2 7 轮ARIA 的不可能差分攻击过程

本文在3.1 节已证明的4 轮不可能差分区分器上构造2 轮前置路径和1 轮后置路径, 得到7 轮不可能差分路径, 如图2 所示. 其中ARIA 算法的最后一轮没有扩散层, 而是密钥加.

攻击过程如下:

步骤1. 定义一个在字节(1,15) 处差分为0, 在其余字节(0,2,3,4,5,6,7,8,9,10,11,12,13,14) 处取遍0–255 的明文空间结构, 这样的空间中含有28×(16−2)= 2112个明文. 每个结构中明文对共有2112×2112×1/2=2223个.

步骤2. 取2N个上述结构, 选取密文对中在(1,2,3,5,8,10,12,13) 这8 个字节处差分为0, 密文对有2N+223×2−8×(16−8)=2N+159个.

步骤3. 猜测密钥k8的8B (k8,0,k8,4,k8,6,k8,7,k8,9,k8,11,k8,14,k8,15), 假设步骤二中保留下来的密文对为(C,C′), 分别进行计算:

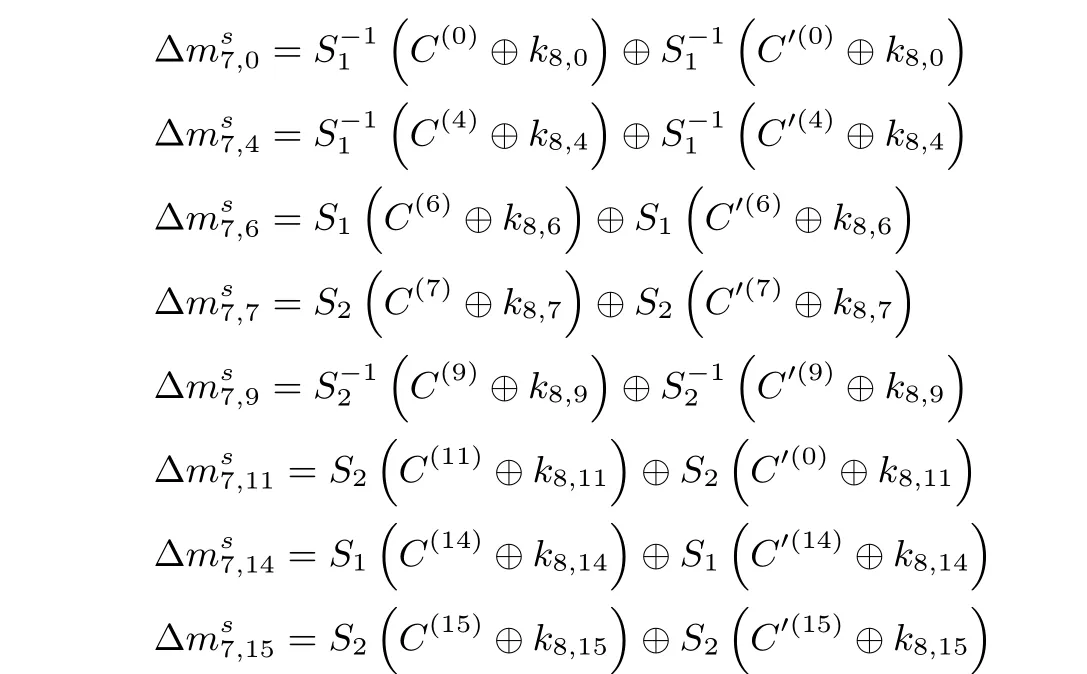
选择满足∆ms7,0= ∆ms7,4= ∆ms7,6= ∆ms7,7= ∆ms7,9= ∆ms7,11= ∆ms7,14= ∆ms7,15的密文对, 还剩余密文对2N+159×2−56=2N+103个.

步骤4. 猜测密钥k1的14 个字节, 并结合推论1 进行分析, 使保留下来的密文对相应的明文对为(P,P′).

步骤4.1. 猜测密钥(k1,2,k1,12), 计算:

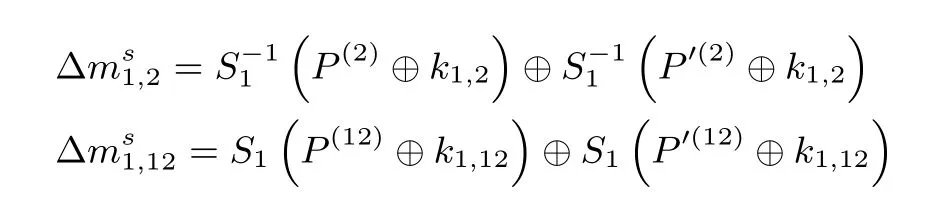
选择满足∆ms1,2=∆ms1,12的明文对, 剩余2N+103×2−8=2N+95个明文对.

步骤4.2. 猜测密钥(k1,5,k1,11), 计算:

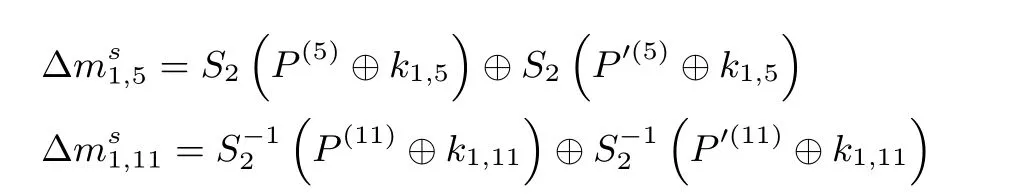
选择满足∆ms1,5=∆ms1,11的明文对, 还剩余2N+95×2−8=2N+87个明文对.步骤4.3. 猜测密钥(k1,6,k1,8), 计算:

选择满足∆ms1,6=∆ms1,8的明文对, 还剩余2N+87×2−8=2N+79个明文对.

步骤4.4. 猜测密钥(k1,0,k1,3,k1,7,k1,9,k1,13,k1,14), 计算:

选择在字节(0,3,7,9,13,14) 处差分满足∆ms1,0⊕∆ms1,3⊕∆ms1,7⊕∆ms1,9⊕∆ms1,13⊕∆ms1,14=0 相应的明文对, 还剩余2N+79×2−8=2N+71个明文对.

步骤4.5. 猜测密钥(k1,4,k1,10), 计算:

选择满足∆ms1,2⊕∆ms1,4⊕∆ms1,5⊕∆ms1,6⊕∆ms1,10=0 相应的明文对,此时还剩余2N+71×2−8=2N+63个明文对.

步骤4.6. 对于步骤4.1–4.5 中的∆ms1, 计算经过扩散层后的差分即∆mo1= DL(∆ms1), 选择∆mo1在字节(1,2,4,5,7,8,9,10,12,15) 处差分为0 的明文对, 结合推论1, 还剩余2N+63×2−24= 2N+39个明文对.

步骤5. 猜测密钥(k2,0,k2,3,k2,6,k2,11,k2,13,k2,14), 计算:

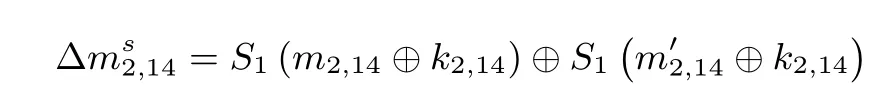
选择满足∆ms2,0= ∆ms2,3= ∆ms2,6= ∆ms2,11= ∆ms2,13= ∆ms2,14且不为0 的明文对, 由于是0 概率差分, 上述所猜测的密钥字节均为错误的, 是需要排除掉的密钥. 通过分析2N+39个明文对, 还剩余248×(1 −2−40)2N+39个错误值, 令248×(1 −2−40)2N+39<1, 得到N =7.

3.3 复杂度分析

下面在分析时间复杂度时应用了“early-abort” 技术[7].

步骤3 中只需要计算8 B 的值, 所以这一步骤需要2×(2166×216+2158×224+ 2150×232+2142×240+2134×248+2126×256+2118×264)×8/16=7×2182次1 轮加密运算.

在步骤4 中, 只有RKA 和DL 这两种操作, 所以进行每一次运算相当于2/3 的1 轮运算. 所以步骤4 中:

步骤4.1 需要232×2×2110×216×2/16×2/3=1/3×2157次1 轮加密.

步骤4.2 需要232×2×216×2102×216×2/16×2/3=1/3×2165次1 轮加密.

步骤4.3 需要232×2×232×294×216×2/16×2/3=1/3×2173次1 轮加密.

步骤4.4 需要232×2×248×286×248×6/16×2/3=2213次1 轮加密.

步骤4.5 需要232×2×296×278×216×2/16×2/3=1/3×2221次1 轮加密.

步骤4.6 只有DL 操作, 需要232×2×2112×270×1/3=1/3×2215次1 轮加密.

步骤5 需要232×2×2112×(246×216+238×224+230×232+222×240+214×248)×6/16 =15×2204次1 轮加密.

所以总的时间复杂度:(7×2182+1/3×2157+1/3×2165+1/3×2173+2213+1/3×2221+1/3×2215+15×2204)×1/7 ≈2216.

综合而言, 7 轮的攻击复杂度为: 2112+N=2112+7=2119数据复杂度和大约2216次7 轮加密运算.

4 总结

本文提出了一个新的4 轮不可能差分路径, 根据ARIA 算法的结构特征, 第3 节中, 在4 轮不可能差分区分器上构造了2 轮前置路径和1 轮后置路径, 实现了7 轮ARIA 算法的不可能差分分析. 此路径下,7 轮不可能差分分析共需要2119选择明文和大约2216次7 轮加密运算. 与表2 相比, 减少了时间复杂度.

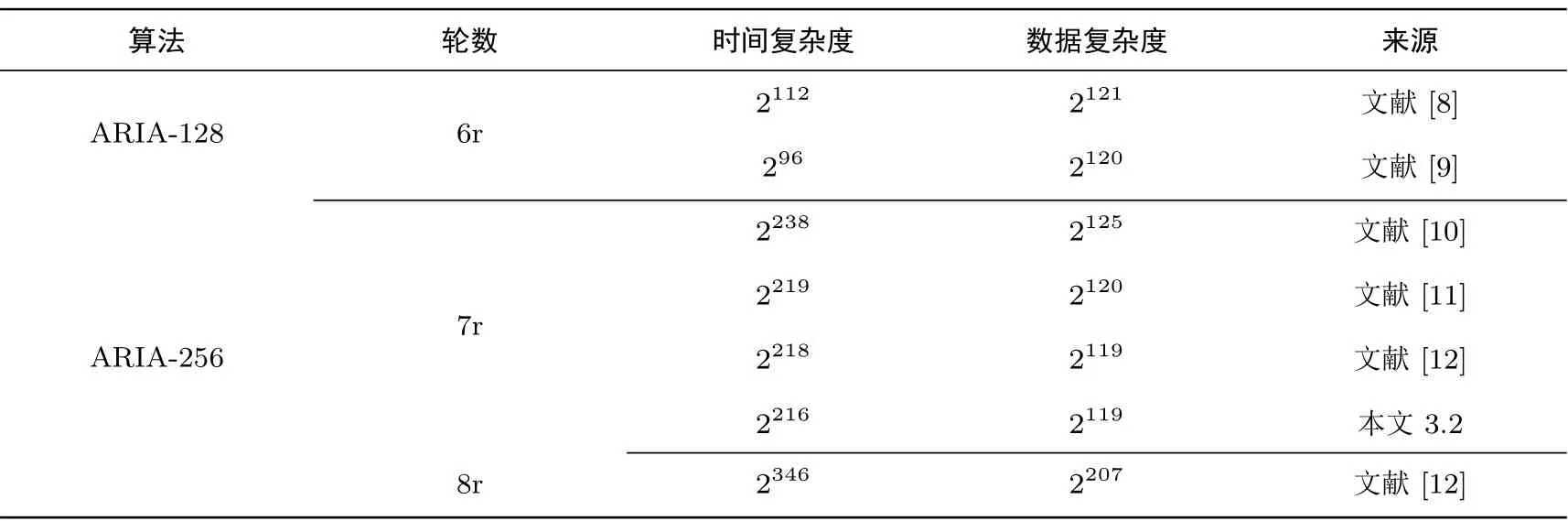
算法 轮数 时间复杂度 数据复杂度 来源ARIA-128 6r 2112 2121 文献[8]296 2120 文献[9]ARIA-256 7r 2238 2125 文献[10]2219 2120 文献[11]2218 2119 文献[12]2216 2119 本文3.2 8r 2346 2207 文献[12]

在以后的研究中, 希望能够寻找到新的不可能差分路径, 尝试用不同的密钥恢复技术来降低7 轮ARIA 算法不可能差分分析的复杂度, 再进行8 轮不可能差分分析, 重点在于降低8 轮不可能差分分析的复杂度, 使得其时间复杂度、数据复杂度低于穷搜的攻击复杂度.