一种基于Rule30+ 细胞自动机的流密码设计方法*
2020-09-12郭晓威郭亚军
郭晓威, 郭亚军
华中师范大学 计算机学院, 武汉430079
1 引言
细胞自动机首先由冯诺伊曼[1]提出, 这是一种研究复杂系统的理论模型. 在1986 年, S. Wolfram 通过简化细胞自动机的行为, 首个提出使用细胞自动机来设计流密码[2]. 这种流密码的设计基于Rule30, 能够输出随机性质良好的密钥流, 同时安全性可以归结于NP 问题. MS 攻击[3]由Meier 等人在1992 年提出, 这是一种针对该结构的攻击方式, 它根据结构中存在的线性相关性进行攻击, 并指出需要超过1000 长度的Rule30 细胞自动机, 才能实现其计算上的安全. 目前基于细胞自动机设计流密码主要包含两种思路,一种是设计更复杂的规则, 如CARPenter[4], 它选择了一种5 邻域规则的细胞自动机来作为流密码的非线性部分. 另一种是设计更复杂的结构, 如CAR30[5]或者CASTREAM[6]. 之所以会不断有学者尝试使用细胞自动机设计流密码, 这主要是基于两个原因. 首先, 细胞自动机的结构具备并行特性, 这种性质能够很好的由硬件在较小的开销下实现. 第二, 一个设计良好的流密码往往能够作为伪随机数发生器使用, 基于细胞自动机能够设计出性能良好的伪随机数发生器[7–9]和真随机数发生器[10]. 并且, 细胞自动机一个独特的优势在于规则编码, 编码后的规则可以使用编辑距离来判断两个规则是否相似, 并且表征能力良好.这种特性使得在确定了适应度函数后, 可以通过进化算法去自动的生成所需要的规则或者规则集[11,12].
Rabbit[13]和Grain-v1[14]是ESTREAM 项目[15]中进入了final list 的两种流密码设计结构. 前者是一种基于复杂系统理论设计的流密码算法, 它包含513 个内部状态, 具有很好的安全性, 但在效率上与后者相比略显不足. 它的一个启发意义在于, 纯粹的基于复杂系统理论模型是可以设计出一个符合现代流密码安全性要求的算法的. 后者是ESTREAM 硬件组的优胜者, 它的结构包含一个线性模块, 非线性模块和输出函数, 各个模块间满足一定的依赖关系. 这种结构层次非常清晰, 符合这种设计思路的流密码都可以归属为Grain Family. Grain 算法自提出以来经过了好几次的修改, 比如Grain-v1 被认为无法抵抗线性逼近攻击[16], 于是Grain-128[17]通过修改结构中线性结构与非线性结构的反馈函数以及输出函数,解决了相关性问题. 我们注意到, Grain 算法的安全性很大程度的依赖于结构中的反馈函数以及输出函数,这使得当密钥长度发生变化时, 结构中所有的函数都需要重新设计. 将细胞自动机引入到Grain 型结构的设计中, 可以使得流密码在具备相当安全性的情况下, 同时具备对任意长度密钥的适配性.
在上文提到的CAR30[5]就是一种属于Grain Family 结构, 同时具备适应任意长度密钥的流密码设计, 当设计需要适配新密钥长度的时候, 只需要修改结构中对应的内部状态数, 而不需要像Grain 一样重新设计流密码算法. CAR30 中包含3 个128 bit 长的细胞自动机, 一共384 个内部状态. CAR30 的问题在于, 硬件的开销较大, 在该设计思路下很难快速的产生密钥流. 这主要是因为算法在执行过程中包含循环操作, 引入循环操作本身会带来额外的硬件开销. 并且, 由于不同模块间的循环操作不能很好的并行进行, 还需要加入同步的控制信号. 这使得算法无法以时钟周期为单位输出密钥流, 从而在设计层面上限制了产生密钥流的速度.
本文提出一种新的流密码设计思路, 算法属于Grain Family 结构. 我们对Rule30 进行了改进, 称之为Rule30+. Rule30+ 依然属于一种简单的规则, 之所以本文没有使用5 邻域规则, 这主要是因为5 邻域规则的引入会带来较大的硬件开销, 与流密码目前的定位不太符合. 基于该规则设计非线性模块使得算法能够解决Rule30 所引发的线性相关性问题, 即能够抵抗MS 攻击. 同时较CAR30 有着更小的硬件开销与更快的密钥流产生速度.
论文的组织如下, 首先在第2 节中介绍与算法设计相关的预备知识. 在第3 节中会给出Rule30+ 的介绍和算法的详细设计与伪码实现, 随后在第4 节和第5 节分别对算法的随机性和安全性进行分析, 最后在第6 节给出算法的硬件开销与结论.
2 相关知识
2.1 一维细胞自动机
细胞自动机是一个具有时间与空间概念的动态系统, 它由多个细胞构成, 细胞的排列方式可以是1 维的, 比如向量, 也可以是2 维的, 如矩阵, 或是是高维的. 我们使用c0,c1,c2,··· ,cn−1来表示细胞自动机,n 为细胞的个数, 在一维细胞自动机中等于向量长度. 对于细胞而言, 在给定的时刻t, 它都会拥有状态要sti和状态转移函数f(ci), f(ci) 用于确定t+1 时刻下该细胞的状态, 即有st+1i= f(ci). 本论文中探讨的是在GF(2) 下的一维细胞自动机, 此时细胞状态的取值只能是0 或者1. 为了方便之后的叙述, 我们记t 时刻下长度为l 的细胞自动机状态(st0,st1,··· ,stl−1) 为St. 记细胞ci自t 时刻起所产生的状态序列(sti,st+1i,··· ,st+k−1i) 为Cti, 且有Cti的长度为len(Cti)=k. 在接下来比较的过程中, 对于起始时间相同的Cti间的对比, 会将其简写为Ci, 或称之为第i 列.
2.2 一维细胞自动机的相关概念
2.2.1 细胞半径
细胞半径用来确定一个细胞存在多少“邻居”, 当细胞半径为d 时, 一个细胞有2d+1 个邻居. 具体的来说, 对于ci,cj, 如果|i −j|≥d, 那么我们可以认为两个细胞是相邻的. 当d=1 时, 即是一般意义上的相邻. 当且仅当两个细胞处于相邻关系时, 细胞之间才可能会有关联性, 这种关联性体现在状态转移函数上, 细胞是自相邻的.
2.2.2 规则
规则是在指定细胞半径下用来描述细胞状态转移函数的一种概念, 一般可以用一个具体的状态转移函数描述规则. 特别的, 对于细胞半径为1 的一维细胞自动机, 一般以数字作为规则的代号. 比如本文开头提到的Rule30, 这是一种细胞半径为1 的规则, 一共有256 种这样的规则.
2.2.3 混合和简单细胞自动机
“简单” 指细胞自动机中, 所有细胞都服从相同的规则. 相对的, 当至少存在两个细胞, 它们服从不同的规则的时候, 那么就称这种细胞自动机是混合细胞自动机, 混合细胞自动机可以是细胞间规则不同, 也可以是一个细胞在不同时刻下, 或是在其他条件下, 服从不同的规则.
2.2.4 边界条件
一维细胞自动机的细胞排列为向量, 这使得第一个元素和最后一个元素在细胞半径为1 时, 均只有两个邻居. 为了使得细胞自动机中所有的细胞都具有相同的邻居数量, 需要引入边界条件. 常见的边界条件包括0 边界, 1 边界, 循环边界和镜像边界. 一般而言, 边界条件是对称的, 即左, 右两侧选用相同的边界条件.
表1 是一个关于规则30 的描述, Status 代表的是邻居的状态, Next 代表的是下一个时刻细胞的状态.以101 为例, 它代表对于指定细胞c, 当左侧细胞状态为1, 本身状态为0, 右侧细胞状态为1 时, 下一个时刻细胞c 的状态为0. 可以看到,Next 行中8 个状态所组成的二进制数(00011110), 转化为十进制就是30.

表1 Rule30 状态转移表Table 1 Status transform table of Rule30
2.2.5 线性细胞自动机和非线性细胞自动机
对于线性细胞自动机, 可以使用线性变化T 来描述不同时刻下细胞自动机状态的关系, T 由细胞自动机所服从的规则确定. 如果细胞自动机的状态变化不能用上述的表达式来进行描述, 那么就称为非线性细胞自动机. 例如, 对于0 边界, 规则90 的细胞自动机, 有

3 设计思路
3.1 Rule30+ 及其性质
在给出流密码的详细设计之前, 我们先介绍Rule30+. Rule30+ 的更新函数与Rule30 类似, 两者的状态转移方程如下. 另外, 本文中涉及的加法均为模2 加法.
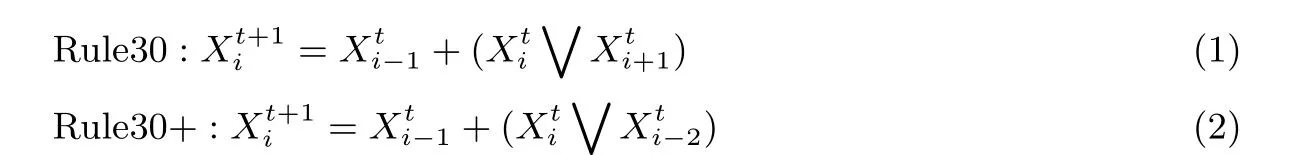
对比Rule30 的更新规则, Rule30+ 不同的地方在于对最后一个细胞的依赖上. 之所以进行修改的原因有两点, 第一, 规则中包含的逻辑操作数量会极大的影响硬件开销, 这使得修改主要在依赖关系上. 第二,通过修改依赖关系使得细胞的状态转移只与其中一侧的细胞相关, 所以只存在一个扩散方向, 这样能够解决Rule30 中的线性相关性问题. 另外, 由于改变的仅是依赖关系, 这使得Rule30+ 能同Rule30 一样保证状态的0/1 产生的频率. 随后, 在边界条件的设置上, 有X0和X1需要应用边界条件.
以下是Rule30+ 的性质, 这些性质可以直接根据状态转移方程得出.

3.2 详细设计
这一节中我们将给出算法的具体设计, 算法一共由256 个内部状态, 即256 bit. 其中线性部分使用119 bit, 非线性部分使用137 bit. 密钥的长度为128 bit, IV 的长度为112 bit. 对于线性部分, 我们使用si来表示第i 个位置的状态, 同理对应非线性部分, 我们使用bi来表示第i 个位置的状态. 下面, 我们将按照非线性模块、线性模块、输出函数三个部分对流密码的结构进行说明.
对于流密码的非线性部分, 我们基于Rule30+ 进行设计, 称之为CA30+, 其状态转移方程同(2), 其中边界条件b−1,b−2的设置如下

当且仅当算法处于初始化阶段时, a=1, 且Zt代表此时的输出. 其中, b−1用于保证CA30+ 对CA90 直接的依赖关系. 而之所以b−2的变换取决于CA90, CA30+ 以及Zt, 原因如下. 第一, 包含CA90 的状态能够改善b−2在统计意义上的随机性, 同时使得b136依赖更多CA90 的状态. 第二, 虽然CA90 在初始化阶段中边界条件与Zt相关, 但在已知IV 的情况下, 由于CA90 的扩散需要时间, 这使得攻击者仍可以推断出一部分s60序列, 于是在初始化阶段中引入Zt, 可以使得攻击者无法确定Zt+s60的值. 第三, 由引理2 可知, 若b−1,b−2的变化仅与CA90 相关, 那么存在时刻t, 使得CA30+ 的状态在t 时刻后仅与CA90 相关, 而与密钥的选取无关. 这使得b−2的变换需要引入CA30+ 状态的影响. 另外, 其中需要引入的CA30+ 状态数与CA30+ 的长度有关, 其最终关联的状态数应在log2l 左右, l 为CA30+ 的长度, 同时其位置应满足均匀分布.
对于线性部分, 一般的设计思路是使用Rule90 和Rule150 在零边界下设计一个满周期细胞自动机[18], 这种情况下对细胞自动机的长度没有限制. 事实上, 线性反馈移位寄存器(LFSR) 和90–150 细胞自动机产生的随机序列具有相当的随机性能, 并且较之前者, 有更大的线性复杂度, 同时在长度较大的情况下, 更容易在硬件中实现[19]. 本文基于Rule90 在镜像-零边界下设计线性部分, 称之为CA90. 这主要是因为Rule90 较Rule150 有更小的硬件开销和更快的运算速度. 这种方式的问题在于对细胞自动机的长度进行了限制, 只有满足特定条件的长度才能成为满周期细胞自动机, 119 bit 就是一个满足上述要求的长度[20]. 以下是Rule90 和Rule150 的状态转移方程

对于本文所使用的Rule90, 其状态转移方程同式(5), 它们的不同点在于处理边界值的情况. 以下是0 边界Rule90 和本文使用的Rule90 在镜像边界上的状态转移方程.
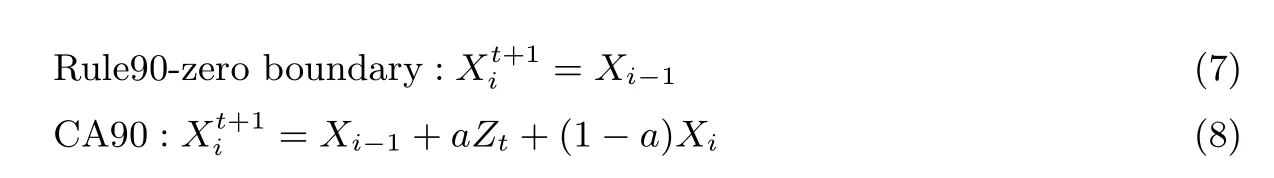
其中, 当算法处于初始化阶段时, a=1, 在密钥流输出阶段, a=0.
最后在输出函数部分, 本文使用的输出函数为

之所以输出函数较Grain-128[17]显得比较“简单”, 这主要是因为在Grain-128 中的非线性部分, t+n 时刻下新产生的内部状态已经在非线性反馈移位寄存器中(NFSR) 中存在了n 个时钟周期了, n 为NFSR的长度, 这使得攻击者可以追溯t 时刻下NFSR 的情况, 并利用两者的相关性去推断出线性结构的内部状态. 对于本文中的非线性状态b136, 它是经过多次不可逆状态转移方程的迭代后完成的, 具有很高的线性复杂度, 这是本文选择该输出函数的原因.
如图1 和图2 所示,流密码的运行阶段分为两个部分,一个是初始化阶段,另外一个是密钥流输出阶段.在初始化阶段, 算法首先将Key 和IV 分别装载到CA30+ 和CA90 中. 设ki代表Key 的第i 位, 同理, vi代表IV 的第i 位. 设密钥长度为lk, 初始化向量的长度为li, CA30+ 的长度为l30, CA90 的长度为l90, 于是有bi+1= ki(0 ≤i < lk), 以及si= vi(0 ≤i < li). 随后, 将b0,si(li≤i ≤l90) 置为1, 将bj(lk≤j ≤l30) 置0. 另外, 在初始化阶段, 算法不产生密钥流. 最后执行轮数r = 256 后(r 应至少大于算法中包含的内部状态数), 完成初始化操作. 在密钥流输出阶段, 算法在每个单位时钟周期下都会产生1 bit 的密钥.
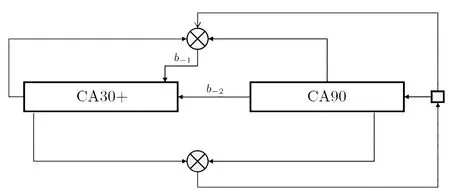
图1 初始化阶段Figure 1 Initial mode
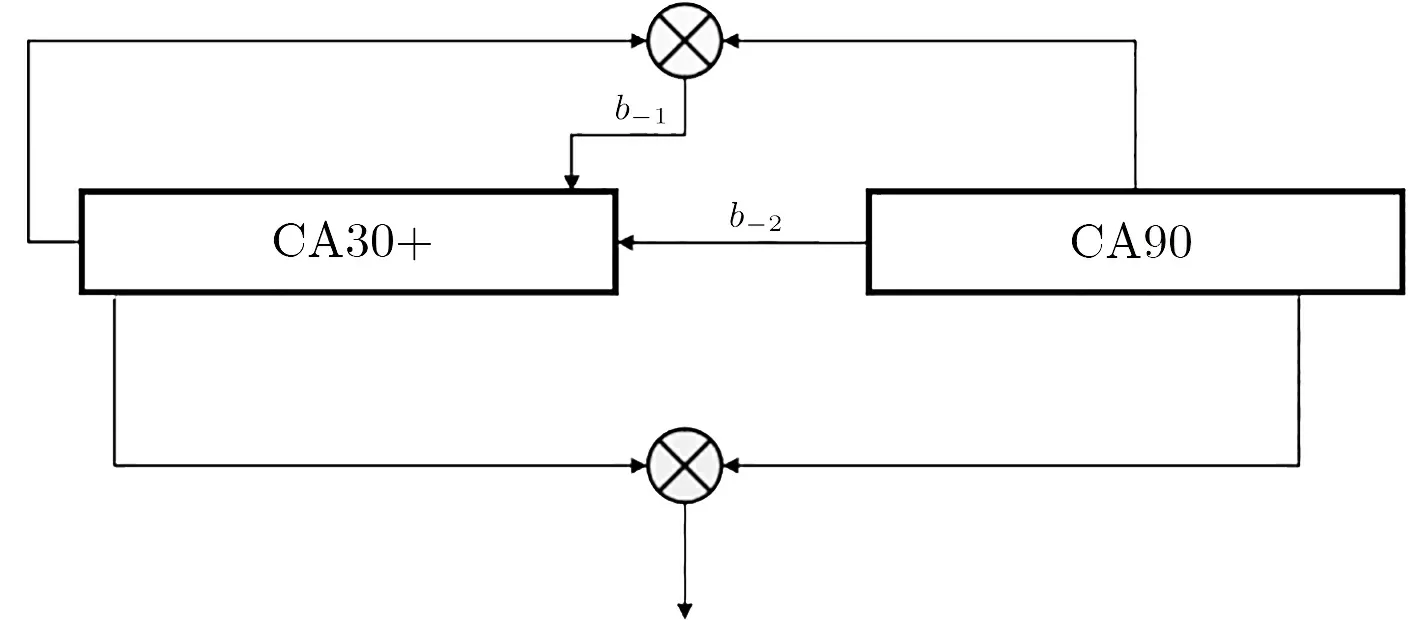
图2 密钥流输出阶段Figure 2 Output mode
3.3 算法伪码
算法总体结构如伪码1所示, 伪码2代表一个时钟周期下, 算法完成具体的操作. 每完成一次Round 函数, 都会更新一次变量Output 的值. 算法首先分为初始化阶段, 密钥流输出两个阶段. 在初始化阶段将Key 和IV 载入到CA30+ 和CA90 中. 对于算法中涉及到的运算操作, 这些操作是以bit 为单位进行的.特别的, 对于软件环境下的算法实现, 可以通过以byte 为单位事先建立代换表和置换表的方式, 来加快算法的执行速度, 使用该方法需要额外占用2 KB 的内存空间.

伪码1 流密码结构Load Key, IV to CA30+ and CA90.#Initial Mode for i in 0 to 255 do Round();end#Output Mode for i in 0 to LengthOfKeyStream do Round();Add Output To KeyStream;end伪码2 函数Round#CA30+for j in 0 to 136 do# when j = 0 or j = 1, need to call boundary condition CA30+Temp[j] = CA30+[j −1] XOR (CA30+[j −2] And CA30+[j]);end#CA90+for j in 0 to 118 do# when j = 0 or j = 118 need to call boundary condition if on Initial Mode then CA90Temp[j] = CA90[j −1] XOR CA90[j +1];# when j = 118 will do CA90Temp[118] = CA90[117] XOR Output;end else CA90Temp[j] = CA90[j −1] XOR CA90[j +1];end end Swap Temp and CA;Output = CA30+[136] XOR CA90[71];
4 随机性分析
4.1 NIST 随机性测试
本文使用NIST 随机性测试[21]作为算法随机性的检测工具. 它是一种常见的随机性检测方式, 一共包含15 项测试, 分别是频度检验(Frequency)、块内频度检验(Block Frequency)、游程检验(Runs)、块内最长游程检验(Longest Run)、二元矩阵秩检验(Rank)、离散傅里叶变化检测(FFT)、非重叠模块匹配检验(Non Overlapping Template)、重叠模块匹配检验(Overlapping Template)、通用统计检验(Universal)、近似熵检验(Approximate Entropy)、随机游动检验(Random Excursions)、随机游动状态频度检测(Random Excursions Variant)、序列检测(Serial) 和线性复杂度检测(Linear Complexity).
4.2 测试的参数选取和结果概述
本节将对算法的随机性检验结果进行分析, 我们选用了一种基于混沌理论设计的伪随机数发生器, 在下文中称为WQ 算法[22], 作为随机性的对照. 本文调用以系统时间为种子的随机函数为算法生成了Key和IV, 随后使用算法生成了长度为20 MB 的字节流, 编码的方式为二进制. 在NIST 随机性测试的参数选取上, 我们将20 MB 的字节流划分成了20 段, 每一段之间独立的进行NIST 随机性测试, 关于具体到每个测试的参数, 我们采用测试中的默认参数. 最后得出结果如表2 所示. P-Value 为该检测经过归一化的决策指标, 当P-Value>0.01 时, 认为通过该检验, 且值越大, 代表效果越好. WQP-Value 代表WQ 算法在该检验下的P-Value 值. Compare 列代表两者的测试效果对比. 此时我们可以看到, 对于本文所提出的算法, 算法通过了15 项检验, 且在15 项检验中有7 项检验弱于WQ 算法, 有5 项检验强于WQ 算法,具有相当的随机性. 因而, 本文提出的流密码能够产生随机性良好的密钥流序列.

表2 NIST 随机数测试的结果Table 2 Result of NIST random test
4.3 结果分析
随机序列的熵、线性复杂度和长1/0 序列的分布是流密码的设计中比较重要的随机性指标, 这分别对应于近似熵检验、线性复杂度检验、块内最长游程检验. 本节将对这三个检验的结果以及P-Value 值较小的重叠模块匹配检验测试进行分析, 这是因为对于细胞自动机所产生的随机序列, 时间越相近, 关联度越大. 我们将首先介绍近似熵检验, 并以(01101001)2为为例, 说明该检验的执行过程.

图3 左右两侧分布表明了近似熵检测中P-Value 和近似熵的分布情况. 左侧的横轴代表字节段的编号, 由0 到19, 纵轴代表P-Value 值. 右侧的纵轴表示近似熵的取值, 其中maxValue 代表近似熵可以取得的以e 为log 底数的最大值. 本小节中图都将以该形式出现. 由此我们可以看到, 各个字节段的近似熵始终稳定在一个区间, 这说明各个字节段之间随机性质相似. 另外, 由于随机序列的长度有限, 并且很难保证在任意长度下, 0/1 的产生数量完全相等, 这使得序列的熵值必然存在误差. 本文字节段长度的量级为106, 偏差的量级为10−5, 误差在合理的范围内. 算法通过了该检验.

图3 近似熵检验Figure 3 Approximate entropy test
对于线性复杂度检验, 有如下步骤

图4 的左侧是线性复杂度检验的P-Value 分布情况, 右侧为P-Value 取最大值和最小情况下的频数分布情况, 其中, 横轴表示标号为Cx的区间. 且有P-Valuemax= 0.978891, P-Valuemin= 0.035101.由此可以看到, 虽然直观上来看, 两者的分布情况近乎完全一致, 然而P-Value 却有很大的区别, 这说明P-Value 对数据的分布情况非常敏感, 将阈值设为0.01 是严格的, 本文提出的算法通过了该检测.
对于块内最长游程检测, 其关
注点在于块内最长的1 序列. 该检测的步骤如下:
(1) 将序列切分成m 个长度为n=10000 的子块.
(2) 为每一个子块计算其1 序列长度的最大值mi.
(3) 设Ci为1 序列长度最大值为i 的字块数, 使用C10−,C11,C12,C13,C14,C15,C16+记录不同1序列最大长度的子块数量, 最后使用P-Value 判断统计量Ci是否服从卡方分布.
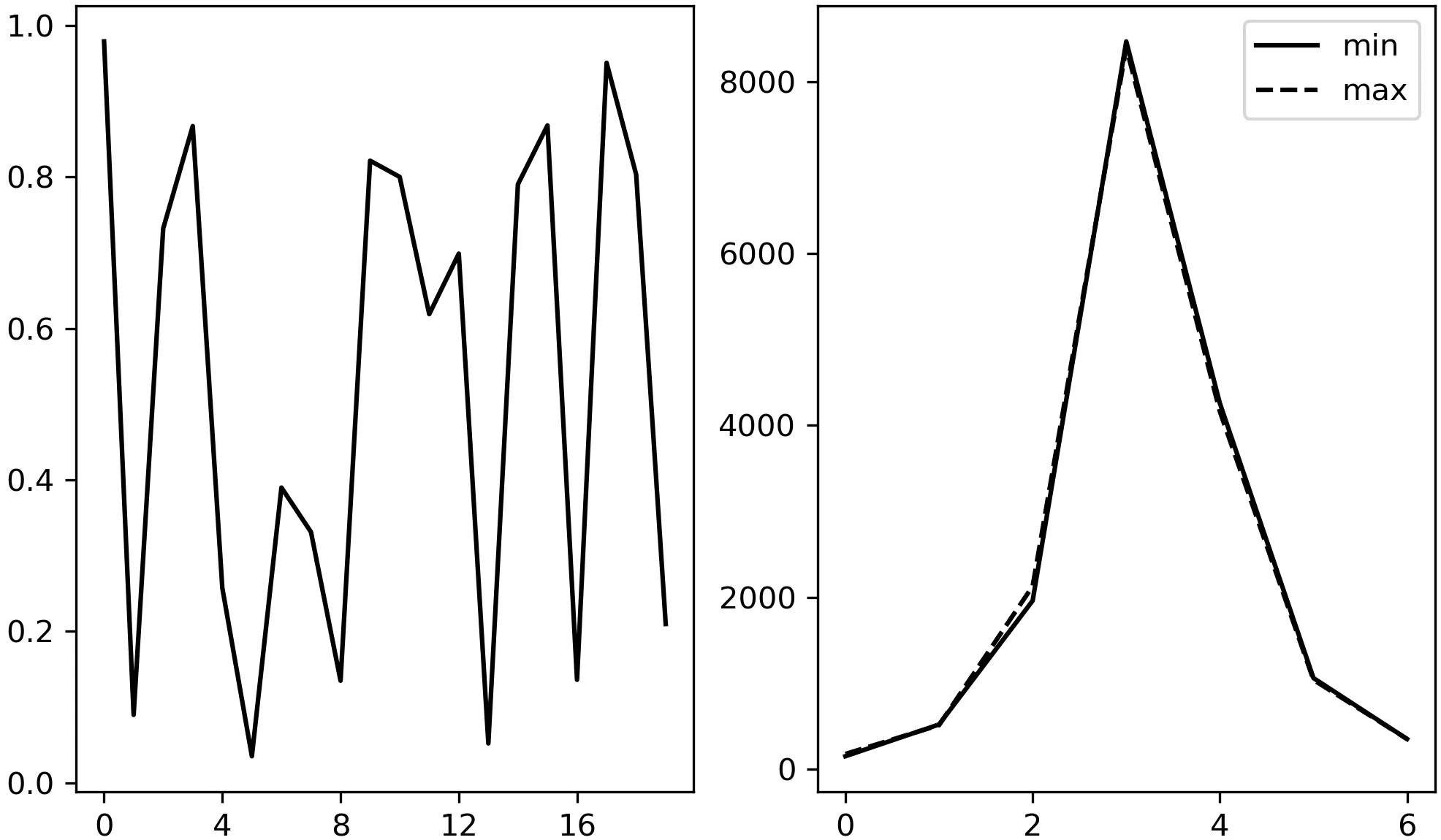
图4 线性复杂度检验Figure 4 Linear complexity test
该检测的依据在于, 一个序列如果是随机生成的, 那么对于长度2n的子块, 出现长度为n 的最长1序列是合理且概率最高的. 图5 说明了P-Value 和以及当P-Value 取最小值和最大值时, 频数Ci的分布情况, 且有P-Valuemax=0.992 138, P-Valuemin=0.04 771. 其中, 横轴代表的是长1 序列的长度, 纵轴代表出现的频数. 其中横轴的边界, 即刻度为10 和16 时, 代表小于等于10 或者大于等于16 的频数. 从图5 可以看出, 两者存在区别的地方在于1 序列最大值大于12 的位置. 但总的来说, 两者在分布上基本一致, 并且众数相同, 因而我们认为两者的随机性质相似. 算法通过了该检验.
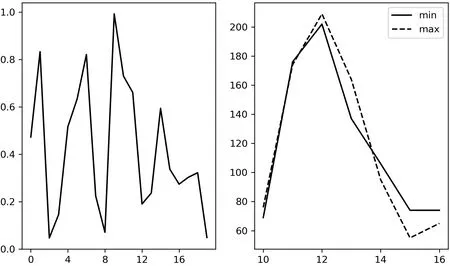
图5 块内最长1 序列Figure 5 Longest run test
重叠模块匹配检验是本文没有通过的随机性检验, 它的过程与模式匹配类似. 以下是它的具体步骤.
(1) 检验首先将切分成N 个长度为M 的子块, 设定模式的长度为m. 在检验中为模式设置了初值.
(2) 模式的匹配过程可以认为是窗口的滑动过程, 每完成一次匹配操作, 窗口将右移一位. 其中, vi代表第i 个子块模式匹配成功的次数.
(3) 设Ci代表匹配成功次数等于i 的子块数量, 使用C0,C1,C2,C3,C4,C5+记录匹配成功次数的分布情况. 其中5+ 代表匹配成功次数大于等于5 的子块数量. 在该检验中, P-Value 表征Ci分布是否服从卡方分布.
图6 代表P-Value 的分布,以及当P-Value 取最大值和最小值时,Ci的分布情况.其中P-Valuemax=0.874 100, P-Valuemin=0.002 812. 虽然对于右侧显示的频数分布中, 决策指标P-Value 相差很大, 但是在两者的频数分布上没有明显区别, 算法通过了该检验.
5 安全性分析
5.1 流密码分析概述
目前常见的流密码分析方法包括穷举攻击、代数攻击、相关攻击、差错攻击、区分攻击、选择IV 攻击、滑动攻击、立方攻击、时间-空间交换攻击(Time-Memory Trade-off Attack)、猜测并确定攻击(Guess and Determine Attack)[24]. 本文我们将基于部分密码分析方法以及针对Rule30 设计MS 攻击[3]进行安全性分析.
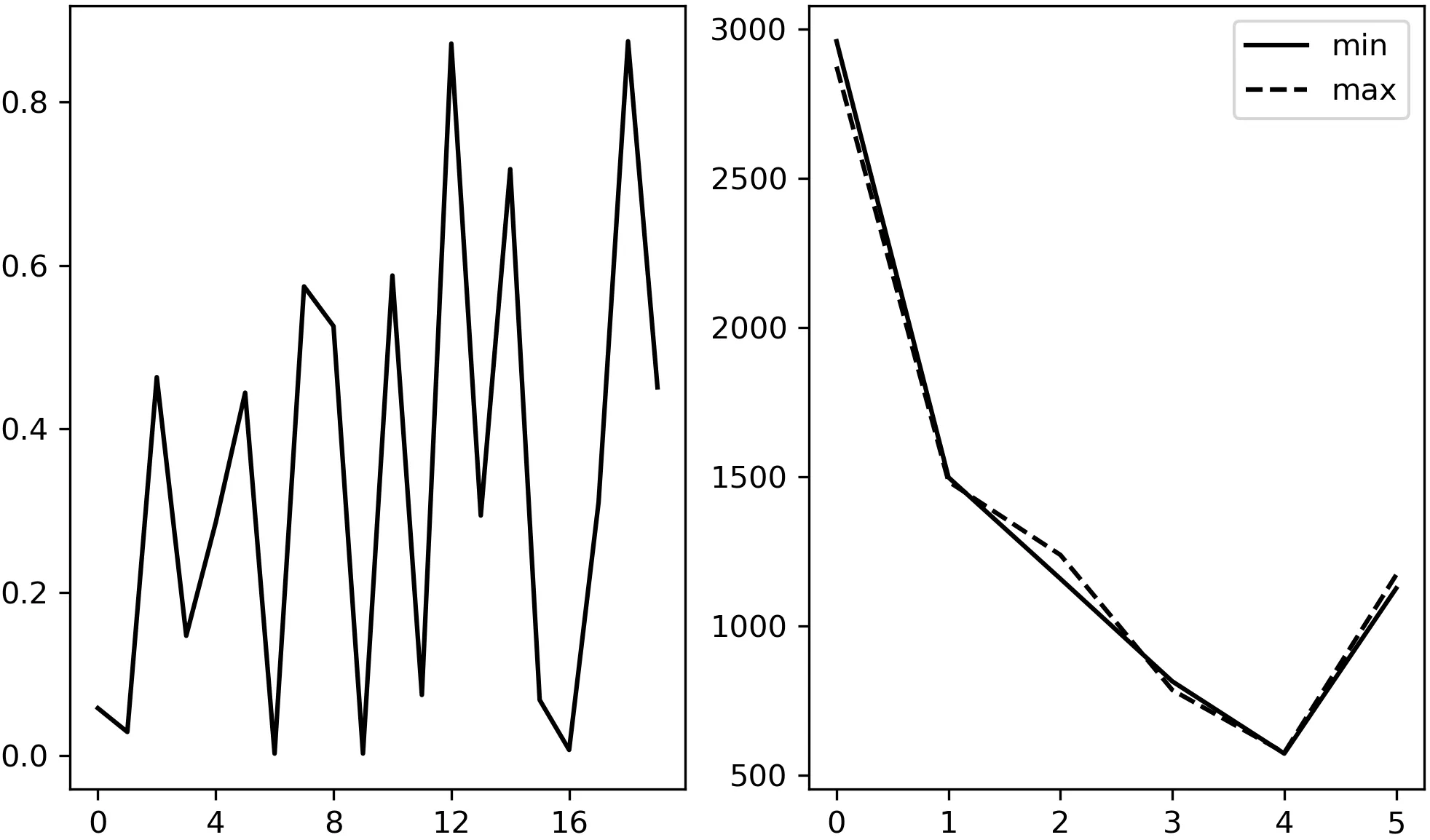
图6 重叠模块检测Figure 6 Overlapping template test
5.2 MS Attack
MS Attack[3]是分析Rule30 的一种方法. 它的思路如下, 它通过猜测一部分细胞自动机的内部状态,并利用结构中存在的线性相关性来恢复细胞自动机的状态, 最后根据密钥流验证猜测的内部状态是否正确. 它被认为能够攻击基于Rule30 设计的非线性结构, 以下是采用MS 攻击对Rule30 进行分析的步骤说明.

由MS 攻击对Rule30 攻击步骤我们可以看到, 如果按照穷举法猜测St, 它的状态空间大小为22k+1,而利用MS 攻击, 则可以将需要穷举的状态空间大小缩小为2k. 我们注意到,MS 攻击中对Rule30 的攻击没有指定Rule30 的边界条件, 这意味着通过调整Rule30 的边界条件使得它能抵抗MS 攻击是不可行的.
对于Rule30+, 为了使得它能够抵抗MS 攻击, 一个核心问题就是阻断上述步骤2 和步骤3 中所描述的bti(i < k) 的链式推导过程. 在MS 攻击对Rule30+ 攻击的场景中, 我们采用与上述Rule30 相同的符号表示, 即是在已知任意时刻下b2k的情况下, 希望能够恢复某时刻t 下细胞自动机状态St. 下面我们来说明Rule30+ 是如何通过阻断链式推导过程, 从而能够抵抗MS 攻击的.
(1) 在猜测部分的选取上, 可以选择b0,b1,··· ,bk或者bk+1,bi+2,··· ,b2k−1, 前者离b2k较远, 在在边界条件未知的情况下, 无法利用已知条件b2k, 因而排除. 于是在猜测部分的选取上, 只能选取后者.

另外, 在上述步骤中, 我们出于符号统一的原因假定了细胞自动机的长度为奇数. 需要说明的是, 无论其长度是偶数或是奇数, 并不影响最后的结论, 即Rule30+ 能够抵抗MS 攻击. 除此之外, 我们也能够看到, Rule30 和Rule30+ 细胞自动机的安全性问题可以归结于求某指定时刻t 下的状态St, 这意味着它的复杂度很大程度上取决于它的长度, 而不是初态的生成方式. 所以, 当需要Rule30+ 细胞自动机适应更大长度密钥的时候, 只需要增大它的长度即可.
5.3 猜测决定攻击
猜测决定攻击的思路如下, 它通过猜测加密算法的一部分的内部状态, 随后试图寻找到某种方式去确定猜测的内部状态是否正确. 比如对于一个包含2k 个内部状态的加密算法, 猜测决定攻击首先选定其中k 个内部状态, 对其进行猜测, 随后试图寻找到一种多项式时间复杂度的方式去验证猜测是否正确, 如果能够找到, 那么只需要对剩下的内部状态继续进行猜测即可. 于是, 猜测决定攻击可以将破解该加密算法的时间开销由22k降到2k+1. 事实上, 我们可以看到猜测决定攻击的关键在于“决定”, 即寻找到验证猜测正确的方法. 注意到, 我们在MS 攻击一节中已经说明了, 即使已知一半的CA30+ 中的内部状态, 也是不能还原CA30+ 状态的. 而如果不能还原CA30+ 的状态, 就无法产生密钥流, 从而使得验证无法进行. 于是,本文提出的算法能够抵抗猜测决定攻击.
5.4 代数攻击
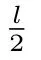

表3 回溯次数与参数个数的对应表Table 3 Corresponding table of number of backtracking times and number of parameters
5.5 时间/空间交换攻击
时间/空间交换攻击是一种以空间换时间的攻击思路,比如事先存储部分密钥与密钥流,该攻击的时间复杂度与加密算法的内部状态数有关. 本文中使用的加密算法一共有256 个内部状态, 因而其时间复杂度不会小于O(2128).
5.6 滑动攻击
滑动攻击主要针对的是使用轮函数的加密算法, 尤其是在轮函数F 较为简单的情况下. 它的核心在于寻找到一组(X,Y), 使得Y =F(key,X) 成立. 此时, 由于轮函数F 较为简单, 且X,Y 均已知, 这使得我们可以很容易的从中得到key. 需要说明的是, 对于(X,Y) 的寻找主要是通过生日攻击的思路进行的, 这使得滑动攻击需要存储足够多的(X,Y). 于是, 滑动攻击本质上仍属于时间/空间交换攻击, 这意味着它的时间复杂度不会小于O(2128).
5.7 线性逼近
线性逼近属于相关攻击, 它的核心思路在于寻找出流密码所产生的密钥流与它结构中线性部分的关系, 其中一个关键的步骤在于利用偏差使用线性结构的内部状态代替非线性变量, 偏差越大, 该方法越有效. 对于本文提出的流密码结构, 非线性结构与线性结构的关系源于b−2,b−1, 而寻找到b136与线性部分的关系需要展开Rule30+ 一共68 次, 于是我们认为寻找到一种同时包含bi和si的等式去表达b136是很困难的, 所以我们认为算法能够抵抗线性逼近攻击.
5.8 选择IV 攻击
选择IV 攻击是假定攻击者可以选择任意IV, 运行流密码, 根据密钥流和IV 的性质来恢复密钥的方法. Grain Family 这种结构天然的对该攻击具有抵抗力, 这是因为虽然IV 是已知的, 但由于在算法初始化阶段中, 密钥会参与线性部分的变化, 这使得在完成初始化操作后, 无法利用线性变化这种方法得知线性结构的内部状态. 事实上, 属于Grain Family 的流密码能够抵抗选择IV 攻击.
5.9 立方攻击
立方攻击属于选择IV 攻击, 它的攻击思想在于将加密系统看作是一个n + m 输入1 输出的, 在GF(2) 域上的多变量多项式p. 其中, n 为密钥的长度, m 为IV 的长度. 随后通过选择不同的IV, 以及在该IV 下的1 bit 密钥流去构建密钥与密钥流的代数关系. 立方攻击中最为在意的指标是d, d 代表p 的维度(degree), 它表示p 中长度最大的项由多少个变量相乘得到. 比如p(x1,x2,x3) = x1x2+x3+x1, 那么此时d = 2. 立方攻击在d 较小的时候有效, 且攻击的时间开销不会小于2d. 对于本文所提出的流密码算法, 如果使用立方攻击进行分析, 那么首先应当确定多项式p 的维度d. 由于多项式p 的输入为密钥和IV, 输出为密钥流, 这意味着p 需要能够描述初始化阶段, 事实上, 表3 给出了回溯次数0 < n < 8 下, 维度d 的变化情况. 由此可以看到, 每对Rule30+ 进行一次回溯, 都会增加所对应多项式的维度. 而我们知道, 算法在初始化阶段需要运行256 次, 这就意味着需要回溯Rule30+256 次. 这就使得多项式的维度d至少不会小于CA30+ 的长度. 由立方攻击的时间开销不会小于2d可知, 使用立方攻击对该算法进行攻击的时间开销不会小于2137.
5.10 差错攻击
差错攻击是一种在算法的运行阶段, 采用某种物理手段引发结构中某个比特的值发生变化, 随后通过观察原密钥流与引入错误的密钥之间的差别, 进而推断出算法内部状态的攻击方法. 事实上, 细胞自动机这种结构对差错攻击存在着天然的抗性, 当细胞自动机的细胞半径为1 时, 任意一个细胞的状态发生变化,都会影响到下一个时刻周围两个细胞的状态变化. 当差错经由扩散函数影响到密钥流时, 细胞自动机已经运行了多次, 这个时候细胞自动机的内部状态已经发生了很大的变化, 从而使得攻击者无法根据密钥流之间的区别推断出算法的内部状态.
6 硬件开销
本小节我们主要讨论算法的硬件开销, 我们分别统计了Grain-128, CAR30, 以及本文所提出算法在相同密钥长度情况下的逻辑门的开销, 具体如表4 所示. 对于细胞自动机而言, 其逻辑门开销主要取决于其所使用的规则和长度. 在规则上, 这主要表现包含的逻辑运算操作数量. 对于Rule30+ 和Rule30 而言, 两者具有相同的逻辑运算数量, 这意味着在相同边界条件下和长度下, 两者具有相同的逻辑门开销.

表4 逻辑门开销Table 4 Cost of logic gate
在开销的量化方式上, 我们与Grain-128 中相同. 即异或运算的开销为2.5, D 触发器为8, 与操作与或操作为1. 于是, Rule30(+) 包含一个异或操作和一个或操作, 其开销为3.5, Rule90 包含1 个异或操作,因而逻辑门开销为2.5, Rule150 包含2 个异或操作, 因而逻辑门开销为5. CAR30 中的线性部分是长度为128 bit 的90–150 满周期细胞自动机, 由于它没有说明具体使用的规则向量, 我们假定其线性部分包含10 个的Rule150, 其余均为Rule90. 可以看到本文提出的算法其硬件开销位于Grain-128 和CAR30 之间, 且与Grain-128 相比开销相差不大. 对于CAR30, 其算法包含循环操作, 并且需要额外的同步信号, 因而其真实的硬件开销将更大.
7 结论
本文提出了一种新的规则Rule30+, 并基于该规则提出了一种新的流密码算法. 本算法的特点在于,首先具备产生随机性良好的密钥流序列的特点. 第二, 较同类算法相比具有更小的硬件开销和更快的密钥产生速度. 第三, 经过简单调整, 即增加CA30+ 的长度和b−2中涉及的CA30+ 状态数, 算法就可以适配任意长度的密钥.
