一种高效的无证书认证密钥交换协议*

曾润智, 王立斌

华南师范大学 计算机学院, 广州510631

1 引言

无证书公钥密码学(Certificateless Public Key Cryptography, CL-PKC) 是基于身份公钥密码学(Identity-based Public Key Cryptography, ID-PKC) 的一个变种, 最初由Al-Riyami 与Paterson 提出[1]以解决ID-PKC 的密钥托管问题. 在传统ID-PKC 中, 用户身份信息(如电子邮箱) 可直接作为用户公钥, 因此无需证书与公钥绑定, 使得ID-PKC 免去与证书相关的复杂操作; 而用私钥钥完全由可信第三方密钥生成中心(Key Generation Center, KGC) 负责生成, 这导致密钥托管问题. CL-PKC 通过增加用户自主生成的本地私密信息来弱化对KGC 的依赖. 在CL-PKC 中, KGC 依然存在并持有系统主密钥,其负责为用户生成部分私钥; 用户在本地生成一个秘密值, 然后根据部分私钥和秘密值组成长期私钥并生成长期公钥. CL-PKC 用户在私钥生成中有一定的自主性, 因此在一定程度上解决ID-PKC 的密钥托管问题.

无证书认证密钥交换(Certificateless Authencated Key Exchange, CL-AKE) 是在无证书体制下的认证密钥交换, 其主要解决如何在无证书环境下双方进行带认证密钥协商的问题, 是重要的无证书密码构件之一. 由于CL-PKC 不存在证书, 恶意攻击者可进行公钥替换以伪装合法用户; 另外, CL-PKC 假设KGC 不完全可信, 其可能会使用系统主密钥窃取用户的某些私密信息. 因此相较于传统的认证密钥交换协议, CL-AKE 协议设计需要考虑的攻击更多, 协议的运算也更复杂. 本文重点关注高效、安全CL-AKE协议的设计.

1.1 相关工作

第一种CL-AKE 协议由Al-Riyami 等人提出[1], 该协议的安全性未在严格定义的安全模型下证明.为严格定义CL-AKE 协议的安全性, Swason 提出了e2CK 模型[2], 该模型基于eCK 模型[3]. Lippold等人增强了e2CK 模型[4], 并提出了第一种可证明安全的CL-AKE 协议. 以上协议都使用双线性配对,使得协议不高效. Yang 等人[5]重新定义e2CK 模型, 使得该模型可更清晰地刻画公钥替换攻击、前向安全等概念. 为了精简描述CL-AKE 安全模型, 本文对文献[5] 中的模型进行一定的修改, 并依然称此模型为e2CK 模型.

无双线性配对CL-AKE 协议的一种设计思路源于Fiore 等人提出的基于身份的认证密钥交换协议[6]. 在该协议中, KGC 使用主秘密为用户身份标识构造Schnorr 签名[7]并作为用户的私钥. 虽然该协议存在漏洞[8], 但现有许多无双线性配对的CL-AKE 协议[9–12]仍借鉴该设计思想, 其中部分方案如文献[9] 也仍然存在类似Fiore 等人协议的缺陷: 攻击者可通过特殊构造的假公钥和临时会话信息, 将密钥计算中用户的部分私钥信息“消元”[10,12], 从而在未知用户部分私钥的情况下伪装任意用户. 近年来部分CL-AKE 协议[13,14]依然存在类似漏洞, 其攻击方式可参考文献[10].

设计CL-AKE 协议的关键问题是, 如何在会话密钥计算中设计合适的信息纠缠, 使攻击者无法通过公钥替换进行伪装, 同时兼顾效率与可证明安全性. Sun 等人方案[10]和Shan 等人方案[12]在密钥计算中加入复杂的信息纠缠来解决公钥替换导致的消元问题. 然而, 为了使安全证明成功, 这些方案存在冗余的计算. 以Shan 等人的方案[12]为例, 为了使协议安全性归约到Gap Diffie-Hellman 假设, 其密钥计算包括了冗余的临时信息与用户长期信息的纠缠, 这制约着协议的运行效率与优化. 本文试图解决该问题.

预计算可用于优化AKE 协议的运行效率[15]. 以KEA+协议[16]、OAKE 协议族[15]为例, 这些协议将会话中可离线计算的部分进行预计算, 从而减少不必要的在线计算, 提高了运行效率. 本文尝试使用预计算技巧来提高CL-AKE 协议的运行效率.

1.2 本文主要工作

本文提出一种高效的无证书认证密钥交换协议OPPRE, 并在随机预言机模型下给出其e2CK 安全性证明. 协议OPPRE 在确保安全性的同时, 避免冗余的会话临时信息与用户长期信息的纠缠, 从而在允许预计算的前提下, 该协议有较高的效率. 同时协议OPPRE 还拥有抗公钥替换攻击、前向安全、抗密钥泄露伪装、抗未知密钥共享等安全属性. 经过对比分析, 协议OPPRE 有较好的安全性和通信、计算效率.

2 预备知识

设S 为一个集合, s ←$S 指从集合S 中均匀随机抽样一个元素s; 若U 是一个用户, 则IDU指用户U 的用户标识符, 以下假定用户标识符和用户一一对应.

2.1 无证书密钥交换

在无证书密钥交换中, KGC 拥有系统主秘密, 并进行系统参数的建立; KGC 根据用户U 的标识符IDU, 使用系统主秘密来生成用户U 的部分私钥. 每个用户在本地生成秘密值, 然后将秘密值和其部分私钥组合为其长期私钥, 用户公钥根据长期私钥生成. 用户之间根据公共信息及自身私密信息进行密钥交换,具体例子可参考本文提出的无证书认证密钥协议OPPRE (图1).

2.2 困难性假设

本文的安全性证明使用到以下难题假设, 设G 是阶为q 的循环群且其生成元为P:

CDH 问题(Computational Diffie-Hellman Problem): 给定(aP,bP), 求abP. 其中a,b ←$Z∗q.

DDH 问题(Decisional Diffie-Hellman Problem): 给定(aP,bP,cP), 判定是否有CDH(aP,bP) =cP(即cP =abP) 成立. 其中a,b,c ←$Z∗q.

GDH 问题(Gap Diffie-Hellman Problem): 给定(aP,bP) 和DDH 预言机, 求解CDH(aP,bP). 其中, a,b ←$Z∗q; 给定任意(aP,bP,cP), DDH 预言机可判定是否有CDH(aP,bP) = cP. GDH 假设定义为: 对于任意多项式时间攻击者, GDH 问题可解的概率是可忽略的.

2.3 安全模型

本文对Yang 等人优化的e2CK 模型[5]进行一定的修改, 并在修改得到的模型上进行协议安全性证明. 本节仅粗略描述e2CK 模型的内容并指出修改的部分, 具体细节请参考文献[5].

e2CK 安全模型定义为攻击者与模拟者的安全游戏, 攻击者控制整个信道, 模拟者负责生成公共信息和用户信息并模拟CL-AKE 协议的运行. 攻击者可发出如下几种类型的问询:

• Send: 攻击者通过该类问询控制用户之间的消息传递, 并指定用户在会话中使用的公钥. 其中,Send0、Send1、Send2分别模拟会话初始方发送信息、应答方接受并应答信息、初始方接受信息的行为.

• Reveal: 该问询允许攻击者泄露相关的秘密信息, 如会话临时秘密、用户的部分私钥、秘密值、KGC 主秘密、完整会话的会话密钥等;

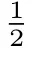
完全泄露与会话新鲜性的定义: CL-AKE 协议会话包含临时秘密、用户部分私钥和秘密值三种秘密信息, 如果会话中三种秘密全部泄露, 则称该会话完全泄露; 一个会话是新鲜的, 当且仅当该会话未完全泄露且未被Reveal 问询, 同时: 若匹配会话存在, 则要求匹配会话也未完全泄露; 若匹配会话不存在, 则要求会话对等方的部分私钥及秘密值未同时泄露. 注意, 若用户的公钥被替换, 则在会话中认为该用户的秘密值被泄露.

安全游戏分为两个阶段. 在阶段1 中, 攻击者可发出上述任意问询, 当攻击者发出Test 问询后, 游戏进入阶段2; 在阶段2 中攻击者可继续进行上述除Test 之外的问询. 安全游戏结束时, 攻击者猜测从Test 问询返回的密钥是sid*的会话密钥还是随机密钥. 如果攻击者猜测成功并且会话sid*是新鲜的, 则称攻击者成功攻击该CL-AKE 协议.

本节安全模型通过Send 问询来刻画公钥替换攻击(详见第4 节), 而不是通过提供“公钥替换问询”来刻画, 这是本文安全模型与其原始版本[5]的主要区别. 两种刻画公钥替换攻击的能力是等价的, 因为它们都允许攻击者欺骗合法用户使用假公钥进行会话建立. 本文通过Send 问询刻画公钥替换攻击的好处为: 一方面, 公钥(来自用户或来自攻击者) 包含在Send 问询的输入中, 标明用户在本次会话中所使用的公钥, 攻击者不再需要额外的问询来进行公钥替换, 这简化了证明过程并清晰地刻画了公钥替换攻击; 另外一方面, 不需要定义额外的事件来判断攻击者是否发出公钥替换攻击, 从而简化证明过程. 原始版本[5]的模型需要定义事件ReplacePK 来判断是否发生公钥替换.

直观上, e2CK 安全的CL-AKE 协议要求: 若会话及其匹配会话不被完全泄露, 则会话密钥不泄露;若不存在匹配会话(对等方不存在对应临时秘密), 则要求在会话不被完全泄露, 且会话对等方部分私钥及秘密值不同时泄露的情况下, 会话密钥不泄露.

3 协议设计

本节从抵抗攻击、效率、可证明安全性等角度给出CL-AKE 协议设计思想, 并在此思想基础上提出一种高效的CL-AKE 协议.

3.1 设计思想

设xU,sU,tU分别是用户U 的秘密值、部分私钥、会话临时秘密, XU,SU,TU分别是对应的公开信息, 具体含义可参考OPPRE 协议1. 以用户A 与用户B 的密钥交换为例:

• 协议需要保证认证密钥交换的安全属性, 如认证性、抗长期/短期秘密泄露伪装、前向安全性等. 因此A 的会话密钥计算必须包含: xA,sA与XB,SB的纠缠、tA与XB,SB的纠缠、tA与TB的纠缠.

• 为抵抗公钥替换攻击, 协议需要确保, 无论攻击者如何构造XB,TB, 会话密钥始终有tA,sA,xA与SB的纠缠. 否则攻击者可将SB消元从而在未知sB的情况下向A 伪装B. 文献[9,13,14] 中的协议不能达到该要求, 因此存在漏洞.

• 在保证安全性的前提下, 协议需要尽量降低计算量. 从上述内容知, tA,sA,xA必须都与TB,SB,XB有纠缠. 为提高效率, 可考虑混合纠缠, 比如(tA+xA)(TB+SB). 然而混合纠缠的设计必须与可证明安全紧密结合, 以防出现类似文献[9] 的情况.

根据上述思想, 本文尝试从可预计算的角度来设计高效、安全的协议. 考虑如下信息纠缠:

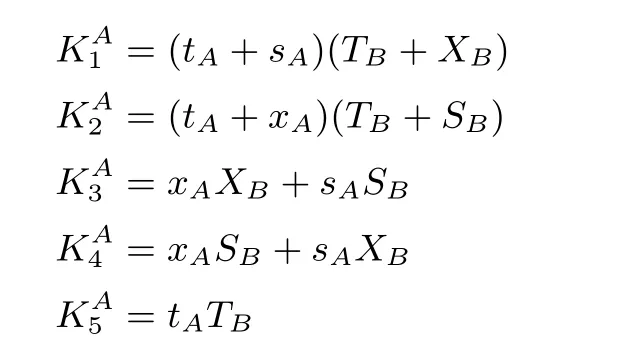
KA1,KA2用以抵抗私钥泄露伪装, 同时确保前向安全性; KA3,KA4,KA5一方面确保攻击者无法将SB完全消元, 另一方面保证可借助随机预言机技巧来完成安全性证明, 其中KA3,KA4不包含临时信息, 因此可进行预计算降低计算量. 综上, 本文提出一种高效的无证书认证密钥交换协议OPPRE (optimal precomputation). 下节给出协议OPPRE 的详细描述.

3.2 协议描述

系统建立: 给定安全参数, KGC 生成一个阶为素数q 的循环群G 及其生成元P, 并选择两个哈希函数h:{0,1}l×G →Z∗q,H :{0,1}l×{0,1}l×G9→{0,1}n, 其中l 是身份标识符的长度, n 是会话密钥的长度, H 作为密钥导出函数. KGC 随机抽取s ←$Z∗q作为主秘密, 并计算系统公钥Ppub=sP, 最后公开系统参数Params=(l,n,q,P,G,Ppub,h,H).

用户部分私钥生成: 给定IDU,KGC 随机抽取rU←$Z∗q并计算RU=rUP,sU=rU+h(IDU,RU)s.然后KGC 通过安全信道返回sU,RU给用户U.

用户秘密值及公钥生成: 用户IDU随机生成xU←$Z∗q作为秘密值, 其公钥为XU= xUP. 用户完整的私钥为(xU,sU).

密钥交换过程: 设用户A 为会话发起方, B 为应答方, 双方密钥交换过程如下:

首先A 随机选择tA←$Z∗q, 计算TA=tAP, 发送MA=(IDA,XA,RA,TA) 给B.

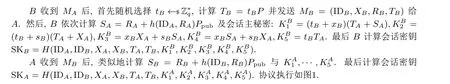
图1 OPPRE 协议Figure 1 OPPRE protocol

由以下等式知A 与B 可建立相同会话密钥:

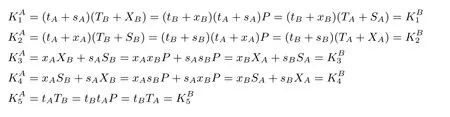
4 安全性证明

证明: 给定GDH 问题实例(aP,bP), 现构造算法S 求解abP. S 首先生成系统主密钥, 并生成系统参数、用户公私钥等信息.

我们通过分类A 在游戏中未泄露的信息来完成安全证明. 设A 选取(Role,IDi,IDj,X∗i,X∗j,T∗i,T∗j)为测试会话, 其中, 会话拥有者为i, Xi,Xj是会话中使用的公钥, T∗i,T∗j是会话中使用的临时会话公钥, Role 标识用户是会话初始方I 还是应答方R. 设x∗i,x∗j,t∗i,t∗j,s∗i,s∗j为i,j 相应的秘密信息,K∗1,K∗2,K∗3,K∗4,K∗5为测试会话的会话主秘密(如图1), 现分类及难题嵌入方法如下:

• 类型1: x∗i,x∗j未泄露, 令X∗i=aP,X∗j=bP.

• 类型2: x∗i,t∗j未泄露, 令X∗i=aP,T∗j=bP.

• 类型3: x∗i,s∗j未泄露, 令X∗i=aP,S∗j=bP.

• 类型4: t∗i,x∗j未泄露, 令T∗i=aP,X∗j=bP.

• 类型5: t∗i,t∗j未泄露, 令T∗i=aP,T∗j=bP.

• 类型6: t∗i,s∗j未泄露, 令T∗i=aP,S∗j=bP.

• 类型7: s∗i,x∗j未泄露, 令S∗i=aP,X∗j=bP.

• 类型8: s∗i,t∗j未泄露, 令S∗i=aP,T∗j=bP.

• 类型9: s∗i,s∗j未泄露, 令S∗i=aP,S∗j=bP.

为完美模拟协议的运行, S 需要维护5 个表hlist,Hlist,Slist,Clist,NClist. 其中表hlist 用于存储A与随机预言机h 的交互, 表Hlist 用于存储A 与随机预言机H 的交互, 表Slist 表用于存储Send0的内容, 表Clist 用于存储所有会话主秘密完整的会话及其会话密钥, 表NClist 用于存储会话主秘密缺失的会话及其会话密钥.

以下我们仅给出类型6 下的安全性证明, 该类型的规约最复杂. 其它8 种类型的证明类似.

类型 6: S 从 p 个用户中随机抽取两个用户 i,j, 并猜测它们的第 k 次会话 (Role,IDi,IDj,X∗i,X∗j,T∗i,T∗j) 作为挑战会话. 不失一般性, 假设i 作为测试会话的初始方.

在类型6 下, S 无t∗i,s∗j(分别为a,b), 因此需要以如下方式构造S∗j对应的R∗j: 首先随机选择l∗j←$Z∗q, 计算R∗j= S∗j(即bP)−l∗jPpub, 并令h(IDj,R∗j) = l∗j. 然后将s∗j作为测试会话参与方j 的部分私钥, R∗j作为j 的部分私钥对应的公共信息. A 问询的模拟如下:

Send0(IDU,IDV): 此问询下IDU作为初始方. 如果(IDU,IDV) = (IDi,IDj), 且该会话是i 与j 的第k 次会话, 即测试会话, 则S 在表Slist 中存入(IDi,IDj,⊥,T∗i(= aP)) 并返回T∗i; 否则, 随机选取tU←$Z∗q, 计算TU=tUP 并返回给A, 然后S 在表Slist 中存入(IDU,IDV,tU,TU).

Send1(IDU,IDV,XV,TV): 此问询下IDU作为应答方. S 检查表Clist、表NClist 中是否已存在相关会话, 存在则返回⊥, 否则S 随机选取tU←$Z∗q, 计算TU= tUP 并返回给A. 然后分成多个情况来继续模拟:

(3) 其它情况: 类似上述情况进行处理.

Send2(IDU,IDV,XU,XV,TU,TV): 该问询的模拟与Send1类似. 以情况(IDU,IDV,XU,XV,TU,TV) = (IDi,IDj,X∗i,X∗j,T∗i,T∗j) 为例, S 无 t∗i,s∗j,x∗j,t∗j, 无法计算 K∗1,K∗2,K∗5中的 t∗i(T∗j+X∗j),t∗i(T∗j+S∗j),t∗iT∗j. S 可类似Send1的情况2 进行处理.

H 问询:(IDV,IDU,XV,XU,TV,TU,K′1,K′2,K′3,K′4,K′5): 随机预言机H 的模拟需要与Send 问询、SessionKeyReveal 问询的模拟一致. 当A 发出了问询, S 首先检查该问询在表Hlist 中是否已存在应答,如果有则返回; 否则S 按如下情况处理:

(1) 情况1: 表Clist 不存在会话(IDV,IDU,XV,XU,TV,TU,∗,∗,∗,∗,∗,∗), 且表NClist 也不存在该会话. 此时S 随机选取SK ←${0,1}n, 返回SK 并在表H 中记录该问询.

(2) 情况2: 表Clist 中存在会话(IDV,IDU,XV,XU,TV,TU,∗,∗,∗,∗,∗,SK). S 取出分量K1,···,K5, 若K′1=K1,··· ,K′5=K5, 则S 直接返回SK; 否则类似情况1 处理.

(3) 情况3: 表NClist 存在会话(IDV,IDU,XV,XU,TV,TU,∗,∗,∗,∗,∗,SK). 此时S 取出该会话的K#值(# 代表有缺失). S 通过DDH 预言机, 判断A 此次问询中是否含有K#中缺失的值,如果有则更新NCL 列表中的这些K#值, 如果所有的缺失值都获得, 则将该会话从表NClist 中删除, 在表Clist 中记录该会话.

特别地, 当(IDV,IDU,XV,XU,TV,TU) = (IDi,IDj,X∗i,X∗j,T∗i,T∗j), S 可通过类似Send1、Send2的处理方式, 获得s∗jX∗i,t∗iT∗j等缺失值. 如果S 获得t∗iS∗j或者s∗jT∗i, 可直接返回该值作为GDH 解并停止模拟.

协议的认证性: 协议OPPRE 具有隐式认证性, 即仅建立会话的双方(长期秘密未完全泄露) 拥有相同的会话密钥, 其中“隐式” 指双方无法确定对方是否已建立相同会话密钥. 由上述证明知, 若攻击者不同时拥有用户的部分私钥与秘密值(对应攻击类型1、3、7、9), 则攻击者无法计算会话密钥. 因此, 协议OPPRE 具有隐式认证性. 在消息交换中加入报文认证码的发送可使OPPRE 协议达到显式认证[17].

5 协议性能分析

本节给出对协议OPPRE 的优化及效率分析, 与相关协议在效率、消息长度、安全性等方面作对比.对比时使用椭圆曲线群来对G 进行实例化, 并对所有协议进行同等的预计算优化. 对比如表1.

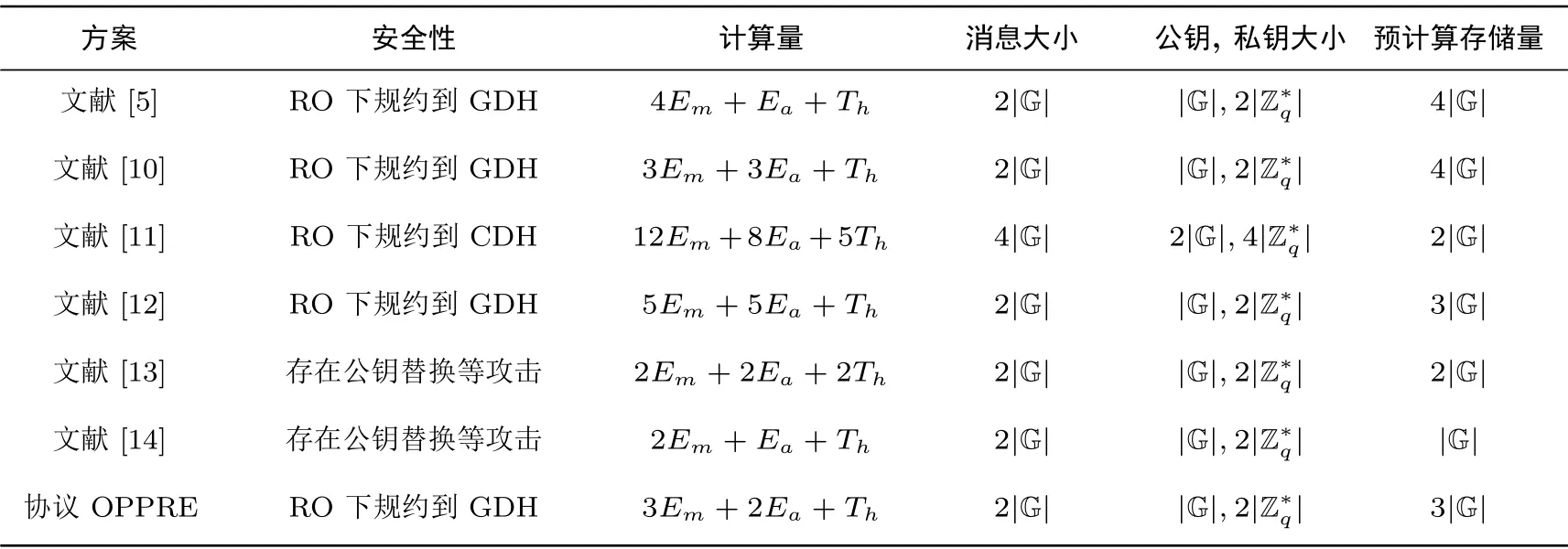
表1 协议效率对比Table 1 Comparison of protocols efficiency

表1 符号解释: Em指椭圆曲线群G 上一次点乘运算的开销, Ea指G 上一次点加运算的开销, Th指一次哈希运算的开销, |G| 指一个G 元素的大小, |Z∗q| 指一个Z∗q元素的大小. RA和TA作为消息的一部分进行考虑.

CL-AKE 协议的预计算.在实际运行中, CL-AKE 用户需要从公共目录中获取对方的公钥, 其中目录中的公钥可能过时或被替换, 但这不影响CL-AKE 协议的预计算, 因为协议会话的建立是在线的, 而公钥的获取、更新、替换等操作都是离线的, 用户可在未建立会话的期间进行公钥的更新、预计算等. 另外,SU作为长期信息可被缓存.

协议OPPRE 的效率优化: 以用户A 与用户B 的密钥交换为例. (xA,sA)是A 的长期私钥, XB,SB作为B 的长期信息可被A 缓存, 因此KA3,KA4可被预计算. KA1,KA2,KA5的构造需要3 次点乘法, 2 次点加法.

由表1 的对比可知, 与其它协议相比, 协议OPPRE 在安全和效率上达到更好的平衡.

6 结束语

本文根据e2CK 模型特点, 给出CL-AKE 协议的设计思路, 并根据该思路提出了一种高效的无证书密钥交换协议OPPRE, 该协议在随机预言机模型下具有e2CK 安全性. 协议OPPRE 避免冗余的会话临时秘密与长期秘密的纠缠, 从而在保证可证明安全性的前提下, 协议可通过预计算提高运行效率. 因此,协议OPPRE 在效率、安全性需求较高的实际场景中(如Ad-Hoc 网络)有较好的应用价值.